| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
La premiÈre hypothÈse concernant la signification de l'onde associée à une microparticule était que la microparticule est en fait une superposition d'ondes planes, qui se propagent ensemble, formant un ainsi dit paquet d'ondes..
L'équation du paquet d'onde est écrite comme ça
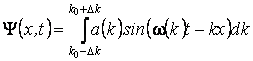
|
|
Chaque onde qui compose le paquet d'ondes se propage avec sa propre vitesse de phase
![]()
tandis que le centre du paquet d'ondes se déplace avec une vitesse, nommée vitesse de groupe, qui est calculée avec la relation de Rayleigh
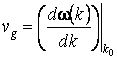
Selon l'hypothÈse de de Broglie, on peut écrire
![]()
Il résulte

Conformément aux relations d'Einstein l'énergie d'une particule est

et l'impulsion s'écrit comme

Il résulte


Par suite
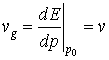
c'est-à-dire la vitesse de groupe du paquet d'ondes a la mÊme valeur que la vitesse de déplacement de la microparticule. Cette constatation semble de consolider l'hypothÈse du paquet d'ondes. Toutefois, bien qu'attirante dans la phase initiale, cette hypothÈse est mise à l'épreuve quand la particule se déplace dans un milieu dispersif. Dans de tels milieux, les vitesses de phase des ondes composantes du paquet d'ondes n'ont pas de valeurs égales et, par suite, le paquet se disperse dans le temps. La dispersion du paquet d'ondes signifierait la disparition de la microparticule. La valeur calculée du temps de dispersion a une valeur beaucoup plus petite que la durée de vie des microparticules, ce qui montre que l'hypothÈse du paquet d'ondes est fausse.
Aujourd'hui, on utilise une autre hypothÈse à l'égard de la signification des ondes associées. Cette nouvelle hypothÈse est basée sur les observations effectuées au cours des expériences de diffraction avec des électrons. Ainsi, on constate que les résultats des expériences sont les mÊmes soit que les microparticules se diffractent simultanément (sous la forme d'un flux intense), soit qu'elles viennent une par une, à seule condition que leur nombre total soit le mÊme. Dans le cas de la diffraction particule par particule, on peut observer facilement leurs points d'impact avec l'écran, leur comportement étant, de ce point de vue, en parfait accord avec la notion de 'particule'. Pourtant, la distribution de points d'impact forme, au fur et la mesure que le nombre de particules tombées sur l'écran croit, la figure de diffraction. La figure de diffraction (et donc le comportement ondulatoire) est à la fin de fins un effet statistique, reproductible seulement en utilisant un trÈs grand nombre de particules. Donc à une particule on ne l'associe pas une onde dans le propre sens du mot, car une vraie onde interagirait simultanément avec tous points de l'écran. Il résulte que les ondes de Broglie associées sont seulement les manifestations des certaines propriétés statistiques des collectifs de microparticules, raison pour laquelle elles sont nommées des ondes de probabilité.
L'interprétation de l'onde associée comme onde de probabilité suppose que la fonction d'onde de la microparticule Y soit dans une certaine relation avec la probabilité que la particule occupe une certaine position dans l'espace. On écrit cette relation comme ça
![]()
oÙ: ![]() est la
probabilité de trouver la microparticule à l'intérieur du volume
élémentaire dxdydz, centré dans le
point de coordonnées x, y et z.
À son tour,
est la
probabilité de trouver la microparticule à l'intérieur du volume
élémentaire dxdydz, centré dans le
point de coordonnées x, y et z.
À son tour, ![]() représente la fonction d'onde, qui, du point
de vue des mathématiques, peut prendre des valeurs complexes. Il résulte
représente la fonction d'onde, qui, du point
de vue des mathématiques, peut prendre des valeurs complexes. Il résulte
![]()
c'est-à-dire la valeur du module carré de la fonction d'onde de la microparticule dans un point donné de l'espace, à un certain instant, représente la densité de probabilité de sa présence à cet endroit la et à ce moment la.
La signification accordée à la fonction d'onde implique ses propriétés mathématiques suivantes:
la fonction d'onde doit Être définie dans tout l'espace
la fonction d'onde doit Être continue et avoir des dérivées continues dans tout point de l'espace
la fonction d'onde doit Être finie dans tout point de l'espace
Ces propriétés conduisent à la conclusion que la fonction d'onde est intégrable en module carré
![]()
Vu que la probabilité de trouver la particule dans n'importe quel point de l'espace représente l'événement certain, il résulte aussi que la fonction doit Être normée
![]()
Connaitre la fonction d'onde nous permettrait à savoir, dans les limites des relations d'incertitude, son comportement ultérieur. Etablir les équations vérifiées par la fonction d'onde associée à la microparticule est l'objet d'étude d'un nouveau type de mécanique, nommée mécanique ondulatoire ou mécanique quantique.
L'équation fondamentale de la mécanique quantique à été postulée par Schrödinger sous la forme suivante
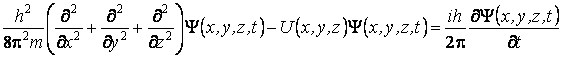
oÙ m représente la masse de la particule, U son énergie potentielle, et ![]() . Cette
équation est considérée valide tant que les résultats obtenus à son aide
ne viennent pas en contradiction avec les faits expérimentaux.
. Cette
équation est considérée valide tant que les résultats obtenus à son aide
ne viennent pas en contradiction avec les faits expérimentaux.
L'équation de Schrödinger a une forme particuliÈre, nommée l'équation stationnaire de Schrödinger, correspondante à l'hypothÈse qu'on peut écrire la fonction d'onde comme
![]()
En introduisant cette expression dans l'équation de Schrödinger, on obtient
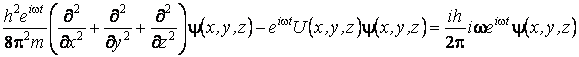
ou
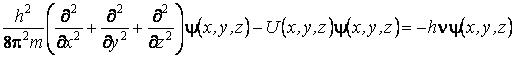
Selon l'hypothÈse de de Broglie, le terme hn représente l'énergie de la particule, ainsi qu'on peut écrire
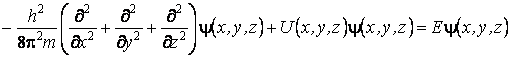
Les solutions de cette équation à dérivées partielles qui obéissent aux conditions imposées à la fonction d'onde sont nommées fonctions propres, et les valeurs correspondantes s'appellent valeurs propres. Par cette raison, l'équation stationnaire de Schrödinger s'appelle aussi l'équation à valeurs propres de l'énergie.
Quand le systÈme est décrit par une fonction d'onde qui est aussi une fonction propre de l'équation stationnaire de Schrödinger, la valeur (mesurable) de l'énergie du systÈme est justement la valeur propre de l'énergie qui correspond à cette fonction propre. Les valeurs propres de l'énergie peuvent Être discrÈtes ou peuvent varier à l'intérieur d'un domaine de valeurs permises.
Tout comme dans le cas de l'énergie, la valeur de n'importe quelle grandeur physique mesurable est dans la mécanique quantique une valeur propre ou une combinaison de valeurs propres d'une équation différentielle à valeurs propres.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2538
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved