| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
|
|
Soit deux systÈmes de référence, S et S', ainsi que S' se déplace avec la vitesse constante u le long d'une direction parallÈle aux axes Ox et Ox'.
Les transformations de coordonnées de Lorentz-Einstein peuvent Être écrites comme ça
![]()
![]()
![]()
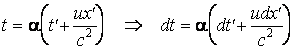
avec
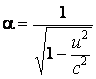
et c = la vitesse de la lumiÈre dans le vide.
On peut calculer les opérateurs suivants
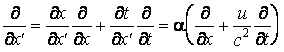

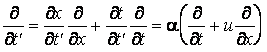
On observe
que l'opérateur ![]() se transforme de mÊme façon que dt, et l'opérateur
se transforme de mÊme façon que dt, et l'opérateur ![]() se transforme de mÊme façon que dx. On sait que le carré de l'élément de
longueur en quatre dimensions
se transforme de mÊme façon que dx. On sait que le carré de l'élément de
longueur en quatre dimensions
![]()
est un invariant relativiste
![]()
En tenant compte des propriétés des opérateurs ![]() et
et ![]() , il
résulte que ceux-ci se transforment de mÊme que l'expression dx2-c2dt2.
Comment
, il
résulte que ceux-ci se transforment de mÊme que l'expression dx2-c2dt2.
Comment
![]()
car dy=dy' et dz=dz', il résulte
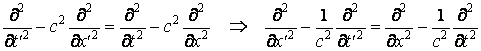
Puisque 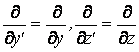 , on peut
écrire finalement la transformation de l'opérateur de d'Alembert
, on peut
écrire finalement la transformation de l'opérateur de d'Alembert
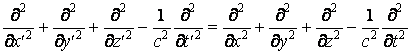
ce qui signifie que l'équation des ondes électromagnétiques en vide reste invariante aux transformations de coordonnées de Lorentz-Einstein. La plus importante conséquence est que la vitesse de propagation des ondes électromagnétiques en vide a la mÊme valeur, égale à la vitesse de la lumiÈre, pour tout observateur inertiel.
Discutons ci-dessous les équations de Maxwell en vide, dans la présence des courants électriques
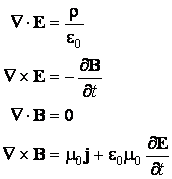
Le fait que la divergence de l'induction magnétique est nulle montre que le vecteur B peut Être écrit comme le roteur d'un potentiel vecteur
![]()
Introduisant l'expression de B dans la troisiÈme équation de Maxwell, il résulte
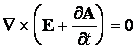
Cette
équation est remplie quand la quantité ![]() est le gradient d'un potentiel scalaire
est le gradient d'un potentiel scalaire
![]()
ou
![]()
Introduisant les expressions des vecteurs E et B dans les deux autres équations de Maxwell, on obtient

ou
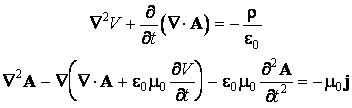
Le potentiel scalaire V et le potentiel vecteur A peuvent Être étalonnés en imposant la condition
![]()
Cet étalonnage s'appelle étalonnage radiatif ou étalonnage de Lorenz.
Utilisant l'étalonnage radiatif, on obtient
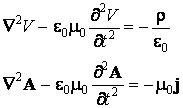
Avec la
notation ![]() , la
condition d'étalonnage et les deux équations des potentiels deviennent
, la
condition d'étalonnage et les deux équations des potentiels deviennent
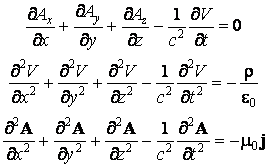
Introduisant les variables
![]()
et les grandeurs

oÙ ![]() , on peut
transcrire les équations de Maxwell sous la forme relativiste
, on peut
transcrire les équations de Maxwell sous la forme relativiste

Avec les notations relativistes, l'équation de continuité
![]()
devient
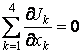
La grandeur physique F F F F F ) s'appelle quadrivecteur potentiel, et la grandeur physique J(J1, J2, J3, J4) s'appelle quadrivecteur courant. Les quadrivecteurs jouent dans l'espace à quatre dimensions le mÊme rôle que les vecteurs dans l'espace tridimensionnel (par exemple, le module d'un quadrivecteur est invariant à la transformation des coordonnées).
La théorie de la relativité restreinte
est basée sur le principe de la relativité, qui affirme que les lois de la
physique ont la mÊme forme dans tout systÈme de référence
inertiel. Par exemple, la relation 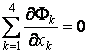 devient en autre systÈme inertiel
devient en autre systÈme inertiel 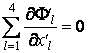 (s'est-à-dire
la quadridivergence du quadrivecteur potentiel est nulle dans tout
systÈme de référence inertiel). Les composantes d'un quadrivecteur se
transforment selon certaines rÈgles quand on change de systÈme de
référence. Déterminons maintenant la modalité de transformation des composantes
du quadripotentiel. On part de
(s'est-à-dire
la quadridivergence du quadrivecteur potentiel est nulle dans tout
systÈme de référence inertiel). Les composantes d'un quadrivecteur se
transforment selon certaines rÈgles quand on change de systÈme de
référence. Déterminons maintenant la modalité de transformation des composantes
du quadripotentiel. On part de
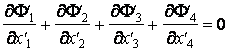
Puisque
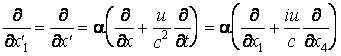
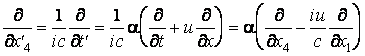
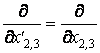
il résulte
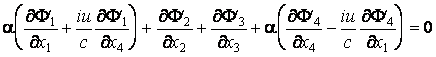
ou
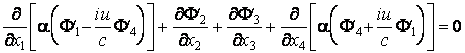
Par la comparaison avec
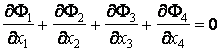
et tenant compte que le module d'un quadrivecteur est invariant
![]()
on obtient les relations de transformation des composantes du quadripotentiel
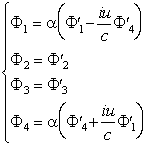
Les relations de transformation des composantes du quadricourant sont

En revenant aux notations non-relativistes (le potentiel vecteur et le potentiel scalaire, respectivement la densité de charge et la densité de courant), on obtient
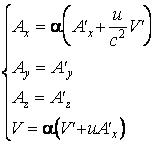
et
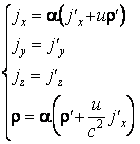
Pour déterminer la modalité de transformation des composantes de l'intensité du champ électrique et de l'induction du champ magnétique on va procéder comme ça:
- on calcule l'expression

- on observe que
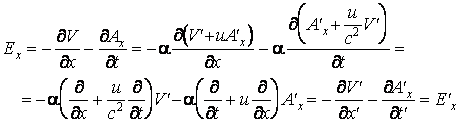


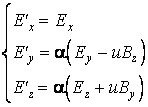
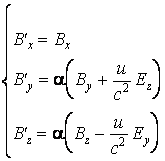
On obtient les relations de transformation des composantes du champ électrique
- soit maintenant l'expression
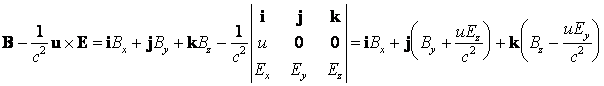
Des calculs similaires conduisent aux relations de transformation des composantes du champ magnétique
Soit la densité totale d'énergie d'une onde électromagnétique
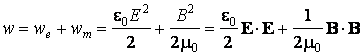
Calculant la dérivée partielle par rapport au temps de la densité totale d'énergie et utilisant les équations de Maxwell, on obtient
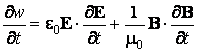
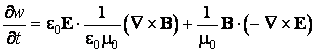
![]()
Comment
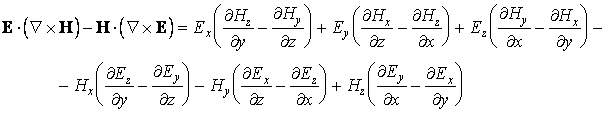 ou
ou

ou
![]()
il
résulte ![]()
Utilisant le vecteur de Poynting, Y = E H , on obtient
![]()
On peut définir le quadrivecteur densité du courant d'énergie par les relations
![]()
et on obtient l'équation de propagation de l'énergie de l'onde électromagnétique sous la forme relativiste
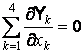
c'est-à-dire la quadridivergence de la densité du courant d'énergie est nulle. La relation exprime la conservation de l'énergie de l'onde électromagnétique.
Les transformations des composantes de ce quadrivecteur sont

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 948
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved