| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Soit une spire circulaire, de rayon R, parcourue par un courant électrique stationnaire, d'intensité I.
Soit aussi un champ magnétique uniforme, d'induction B, oÙ est placée la spire.
On va choisir un systÈme des axes de coordonnées avec l'origine dans le centre de la spire, dont l'axe Oz est perpendiculaire sur le plan de la spire et l'axe Oy est perpendiculaire sur l'induction magnétique.
Soit un élément de longueur dl de la spire, ayant le rayon vecteur
![]()
|
|
On peut écrire
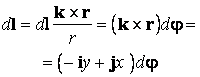
Selon la loi de la force électromagnétique, il résulte
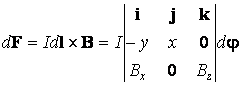
ou
![]()
Les composantes sont
![]()
![]()
![]()
Par l'intégration on va trouver les valeurs des composantes de la force F
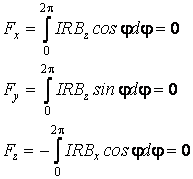
Donc la force qui agit sur la spire est nulle.
Le moment de la force dF par rapport au centre de la spire est

ou
![]()
ou
![]()
Les composantes sont
![]()
![]()
![]()
Par l'intégration, on obtient

Donc
![]()
Sachant que
j = k i
on peut réécrire l'expression du moment de la force comme ça
![]()
Tenant compte que le produit vectoriel k k est nul, on obtient
![]()
ou
![]()
S étant le vecteur surface de la spire. On peut définir maintenant une nouvelle grandeur physique vectorielle, nommée moment de dipôle magnétique de la spire, ayant la formule
m = IS
ainsi que l'expression finale du moment de la force sera
![]()
Ce moment a comme effet une tendance de rotation de la spire autour la droite perpendiculaire sur le plan formé par le moment magnétique et le vecteur induction magnétique, dans notre cas l'axe Oy.
Quand on tourne la spire avec un petit angle da autour l'axe Oy, le déplacement élémentaire de l'élément de longueur dl est
dl1 = kxda = kRcosjda
La force magnétique dépense un travail élémentaire
dL = dF dl1
c'-est-à-dire
dL = -R2cos2j Bsina Idjda
Le travail total pour la rotation de la spire avec l'angle da est
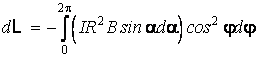
ou
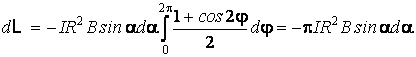
Pour tourner la spire de la position oÙ le vecteur B fait avec le vecteur S l'angle a jusqu'au position oÙ l'angle est a , le champ magnétique dépense le travail
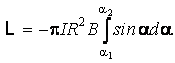
ou
![]()
Ce travail a la signification d'une variation d'énergie potentielle
W - W1 = -L
Vu que les angles a et a sont arbitraires, il résulte
![]()
Par conséquent, l'expression de l'énergie potentielle est définie jusqu'à une constante arbitraire, ayant la forme suivante
![]()
Parce que pR = S, et S B = SBcosa, on obtient
W = -IS B + const
En utilisant le moment de dipôle magnétique m = IS, il résulte
W m B + const
On peut convenir que l'énergie potentielle de la spire est nulle quand les vecteurs m et B sont perpendiculaires, c'est-à-dire quand le moment de la force qui agit sur la spire atteint une valeur extremum. On fixe ainsi la valeur de la constante
const
résultant
W m B
On observe que la valeur de l'énergie potentielle est maximum quand les vecteurs m et B sont antiparallÈles, situation dans laquelle le moment de la force est nul, mais la spire est en équilibre instable. L'énergie potentielle est minimum quand les vecteurs m et B sont parallÈles, situation dans laquelle le moment de la force est nul et l'équilibre est stable.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 756
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved