Pozitionarea GPS, relativa

Pozitionarea GPS, relativa

Fig.1.9. - Vector GPS

Pozitionarea GPS, relativa, are ca scop determinarea unui vector, "baseline", sau a componentelelor vectorului care uneste doua puncte geodezice in care se stationeaza si se receptioneaza simultan cu doua receptoare GPS diferite.

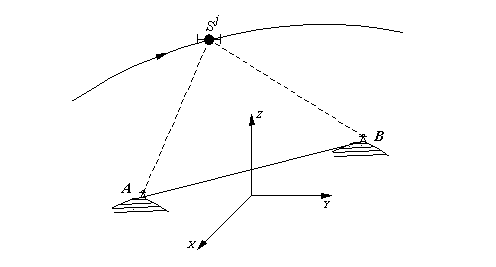
Fie A un punct geodezic cu coordonate geodezice spatiale (ITRFxx, EUREF, etc.) cunoscute si un punct geodezic B, Fig.1.6,considerat punct nou. Coordonatele punctului B, se vor putea determina cu relatiile:

(1.35)

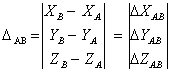(1.36)

Pozitionarea relativa se va putea face fie cu masurarea codurilor, fie cu masurarea diferentelor de faza, care de fapt se aplica curent in practica.

Este necesar sa se faca masuratori simultane cu cel putin doua receptoare, in cazul nostru, amplasate in punctele A si B, care presupunem ca vad in acelasi timp satelitii i,j.

In aceste conditii se pot realiza combinatii liniare, numite diferente simple, duble sau triple. Marea majoritate a softurilor, care prelucreaza masuratori GPS, utilizeaza aceste diferente care folosesc urmatoarele modele matematice.

1 Diferenta simpla

Se cosidera doua receptoare amplasate in punctele de statie A si B, din care se observa simultan, satelitul "j", Fig.1.7, care emite continuu semnale GPS, fara a avea intreruperi, intrerupetri care ar cauza asa numitele "cycle slip".

Fig.1.10. - Diferenta simpla

Se pot scrie, pentru fiecare punct, ecuatiile prezentate in grupul de formule (1.20), respectiv ecuatia pentru masuratorile de faza, atat pentru punctul A cat si pentru punctul B:

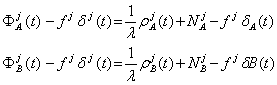(1.37)

Facand diferenta intre cele doua ecuatii, se obtine:

(1.38)

Se poate constata, ca diferenta simpla elimina partea de eroare generata de produsul "f*d(t , generat de asincronismul ceasului de pe satelit, atat cat este comun la cele doua ecuatii.

Actioneaza, in orice caz, in continuare cotele de eroare datorate ceasurilor celor doua receptoare si cotele de eroare datorate termenilor ambiguitatilor de faza.

Ecuatia (1.38) reprezinta ecuatia pentru diferenta simpla in care putem introduce urmatoarele notatii:

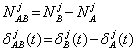(1.39)

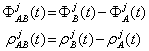(1.40)

si daca se substituie relatiile (1.39) si (1.40), in relatia (1.38), rezulta:

(1.41)

2 Diferenta dubla

Se cosidera doua receptoare amplasate in punctele de statie A si B, Fig.1.10, din care se observa simultan satelitii "j" si "k" care emit continuu semnale GPS cu frecvente identice, adica fⁱ = f^k, fara intreruperi generatoare de "cycle slip", sateliti pentru care se pot scrie doua ecuatii de diferenta simpla conform relatiei (1.41):

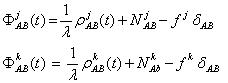(1.42)

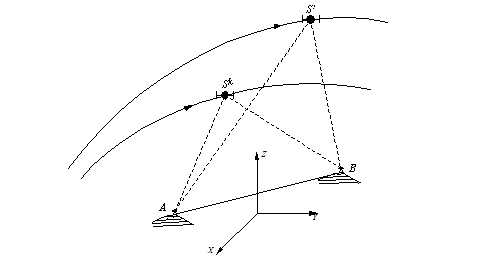
Fig.1.11 - Diferenta dubla

Admitannd ipoteza egalitatii frecventei semnalelor emise de la cei doi sateliti, scazand cele doua ecuatii (1.42) de diferenta simpla, obtinem:

(1.43)

Utilizand notatiile de la grupul de formule (1.38) si (1.39), introduse pentru diferenta simpla, rezulta in continuare:

(1.44)

Formula (1.44), reprezinta ecuatia pentru diferenta dubla si este de notat ca ea elimina erorile generate de ceasurile receptoarelor cu ajutorul celor doua ecuatii ale diferentelor simple si permite determinare necunoscutelor ambiguitatilor de faza.

Eliminarea erorilor datorate ceasurilor receptoarelor este ratiunea si caracteristica de baza a tuturor programelor de prelucrare a masuratorilor GPS.

Aceasta concluzie este asigurata de obligativitatea ca toti satelitii sa emita in aceeasi frecventa, iar observatiile sa fie executate simultan.

Termenii relatiei (1.44) se pot scrie in mod explicit, dupa cum urmeaza:

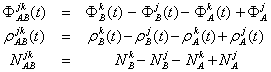(1.45)

3 Diferenta tripla

Pentru a elimina ambiguitatile de faza, necunoscute, Fig.1.11, deoarece acestea sunt independente de timp, Remondi (1984) sugereaza utilizarea diferentei celor doua duble diferente la epocile t₁ si t₂.

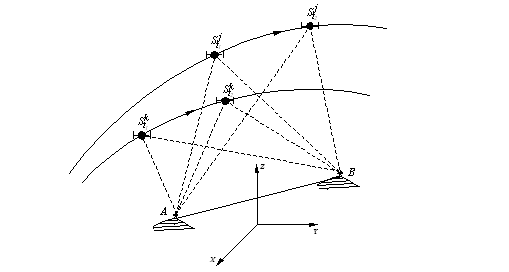
Fig.1.12 - Diferenta tripla

Ecuatia de la (1.44), se particularizeaza pentru epocile t₁ si t₂:

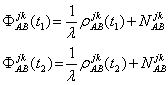(1.46)

Se presupune deasemeni ca observatiile sunt fara intreruperi (cycle slip), conditie in care termenii ambiguitatilor continua sa fie constanti. Facand diferentele celor doua relatii din grupul de formule (1.46), se obtine ecuatia diferentei triple:

(1.47)

care poate fi scrisa in forma simplificata:

(1.48)

Forma desfasurata a triplei diferente, care contine termenii F si r la momentele t₁ si t₂, contine la randul ei, 8 termeni fiecare:

Avantajul principal al triplei diferente, este ca elimina necunoscutele, ambiguitati de faza si din acest motiv tripla diferenta este imuna la schimbarile ambiguitatii de faza (cycle slip).