Analiza si masurarea semnalelor

7.1. Masurarea frecventei

Frecventele semnalelor se pot masura atat pe cale directa, cu aparate indicatoare numite frecventmetre, cat si pe cale indirecta, utilizand montaje speciale.

7.1.1. Masurarea analogica a frecventei

Cele mai cunoscute metode pentru masurarea analogica a frecventei sunt:

metoda directa ;

metoda de punte;

metoda comparatiei;

metoda de rezonanta.

7.1.1.1. Frecventmetre analogice

a) Frecventmetre cu lamele vibrante

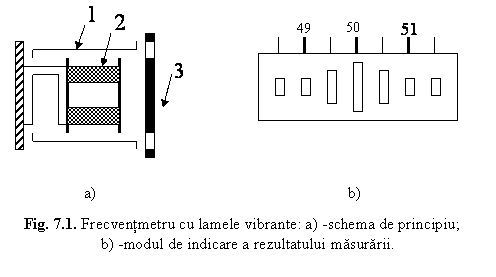
Functionarea acestor aparate se bazeaza pe fenomenul de rezonanta mecanica, care apare sub actiunea unor forte dezvoltate de

un electromagnet parcurs de curent alternativ a carui frecventa f_x se masoara.

Frecventmetrul cu lamele vibrante (fig.7.1, a) consta dintr-o serie de lamele vibrante 1 dispuse pe doua randuri paralele, incastrate la un capat in sasiul aparatului si avand capatul liber indoit in unghi drept. La frecventmetrele cu intervalele de masurare 45 . 55 Hz sunt prevazute lamele din 0,5 in 0,5 Hz.

Frecventa proprie de oscilatie a fiecarei lamele este egala cu dublul valorii frecventei inscrise pe cadranul 3 in dreptul ei. Lamelele sunt supuse vibratiilor cu ajutorul electromagnetului 2, alimentat cu tensiune alternativa, avand frecventa de masurat f_x.

Forta care se exercita asupra fiecarei lamele este proportionala cu patratul inductiei magnetice B, respectiv cu patratul intensitatii curentului i din infasurarea electromagnetului:

f=K₁ B²=K i²=K 2I²sin²(w_xt)=K I²(1-cos2w_xt) (7.1)

Aceasta forta are o componenta continua KI² si una variabila KI²cos2w_xt), cu frecventa dubla 2f_x. Sub actiunea acestei forte, lamelele vor vibra cu frecventa 2f_x, amplitudinea vibratiilor lamelelor este insa neobservabila cu exceptia a 2.4 lamele a caror frecventa proprie de oscilatie este egala sau apropiata de 2f_x si care intra in rezonanta mecanica, vibrand cu amplitudine mare, vizibila de la distanta. Indicatiile apar pe cadran sub forma reprezentata in figura 7.1,b.

Frecventele cu lamele vibrante se construiesc pentru frecvente pana la cca. 1500 Hz, cu 1.4 siruri de lamele. Clasele de precizie ale acestor aparate sunt cuprinse intre 0,2 si 1. Tensiunile nominale sunt de obicei 110 - 220 - 380 -500 V.

b) Frecventmetre cu redresor

Principiul de functionare al frecventmetrelor cu redresor se bazeaza pe obtinerea unui curent redresat avand valoarea proportionala cu frecventa de masurat f_x. Instrumentul indicator care masoara acest curent poate fi gradat direct in unitati de masurare a frecventei. Cel mai simplu frecventmetru cu redresor se obtine prin inserierea unui condensator C cu un instrument magnetoelectric cu redresor (fig.7.2).

Daca la intrarea frecventmetrului se aplica tensiunea u_i=U_msin(w_xt), atunci curentul prin miliampermetru magnetoelectric va fi

Fig. 7.2. Principiul frecventmetrului cu redresor

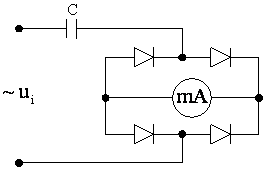
(neglijand rezistenta directa a diodelor si rezistenta instrumentului):

(7.2)

si din relatia (7.2) se obtine:

(7.3)

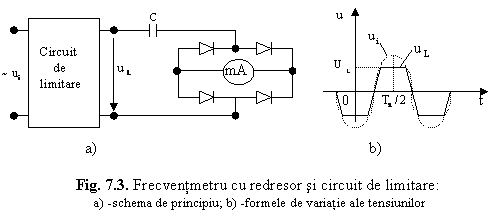
Schema din figura 7.2 are dezavantajul ca frecventa masurata f_x depinde, prin valoarea medie a tensiunii U_med, de valoare maxima a tensiunii de intrare. Pentru ca indicatia instrumentului sa nu depinda de amplitudinea semnalului de intrare (care variaza de la un semnal la altul), intre intrarea aparatului si circuitul de masura se intercaleaza un circuit de limitare (fig.7.3, a), format, de exemplu, din 2 diode Zener, conectate "spate in spate". In acest caz, circuitului de masura i se aplica intotdeauna un semnal de amplitudine constanta U_L, avand frecventa f_x egala cu cea a semnalului de intrare.

Valoarea medie a curentului prin instrument este:

(7.4)

de unde rezulta frecventa masurata:

(7.5)

unde +U_L si -U_L sunt limitele intre care se modifica tensiunea la iesirea circuitului de limitare.

c) Frecventmetre cu convertor de frecventa - tensiune

Frecventa semnalelor cu amplitudine controlata (constanta) poate fi masurata utilizand un convertor frecventa - tensiune (fig.7.4).

Fig. 7.4. Convertor frecventa - tensiune cu AO

Circuitul diferentiaza semnalul de intrare (grupul C₁, R), redreseaza rezultatul (diodele D₁, D₂) si mediaza semnalul obtinut (condensatorul C₂). Tensiunea continua de la iesirea convertorului va fi:

(7.6)

Deoarece    , se obtine:

(7.7)

Se observa ca prin masurarea tensiunii continue U₀ de la iesire, se poate determina frecventa f_x.

d) Frecventmetrele de rezonanta sunt aparate care masoara frecventa prin aducerea la rezonanta a unui circuit LC (fig.7.5). Elementul variabil, de regula, este condensatorul C. Ca indicator al rezonantei se utilizeaza un voltmetru electronic de tensiune alternativa (V.E.) conectat la bornele condensatorului. Principiul de lucru este urmatorul: generatorul a carui frecventa f_x se masoara, se cupleaza inductiv cu bobina de inductivitate L si se variaza condensatorul C pana cand circuitul LC ajunge la rezonanta (voltmetrul avand indicatia maxima). Frecventa se determina cu relatia:

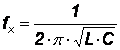
(7.8)

Fig. 7.5. Principiul frecventmetrului de rezonanta

Frecventa de masurat se poate citi direct pe cadranul condensatorului de acord variabil, gradat in unitati de frecventa.

Precizia de determinare a frecventei f_x depinde de precizia cu care se poate pune in evidenta rezonanta in circuitul LC, deci de factorul de calitate Q al circuitului.

Cuplajul dintre generatorul cu frecventa f_x si circuitul LC afecteaza precizia masuratorilor. Cuplajul mentionat trebuie sa fie slab astfel incat sa permita deviatia de cap de scala (deviatie maxima) a acului aparatului indicator. Un cuplaj prea strans intre generator si circuitul LC conduce la deteriorarea factorului Q al circuitului si la modificarea frecventei f_x a generatorului.

Pe acest principiu se bazeaza frecventmetre avand intervalul de masurare cuprins intre 100 KHz - 10 GHz, cu o precizie de ordinul 0,01 - 1%.

Unele frecventmetre de rezonanta folosesc metoda absorbtiei, care se bazeaza pe transferul de energie din circuitul semnalului a carui frecventa se masoara intr-un circuit rezonant cu care este cuplat strans.

In momentul rezonantei, curentul in circuitul semnalului scade la o valoare minima, datorita transferului maxim de energie dintr-un circuit in celalalt. Pentru detectarea rezonantei se utilizeaza un ampermetru montat in circuitul sursei a carui frecventa se masoara (fig.7.6).

Fig. 7.6. Principiul frecventmetrului cu absorbtie

Frecventmetrele de acest tip se numesc frecventmetre cu absorbtie si se utilizeaza atunci cand puterea debitata de sursa este mica, iar masurarea frecventei in conditiile unui cuplaj slab nu este posibila.

7.1.1.2. Metoda de punte

Puntile de curent alternativ, ale caror conditii de echilibru sunt dependente de frecventa, pot fi utilizate, in principiu, pentru masurarea

a) b)

Fig. 7.7. Punti pentru masurarea frecvent:

a) -puntea de rezonanta; b) -puntea Wien - Robinson

frecventei in conditii de laborator. Cele mai raspandite punti pentru masurarea frecventei sunt: puntea de rezonanta si puntea Wien - Robinson.

Puntea de rezonanta (fig.7.7, a) are 3 laturi formate din rezistoare, iar a 4-a latura consta dintr-o bobina (cu parametrii R, L) in serie cu un condensator variabil C, fara pierderi.

Echilibrarea puntii se realizeaza prin varierea capacitatii si a uneia din rezistente. La echilibru sunt satisfacute conditiile:

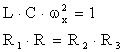
(7.9)

de unde rezulta:

(7.10)

Puntea Wien - Robinson (fig.7.7, b) este alcatuita din 4 rezistoare si doua condensatoare fara pierderi.

Conditiile de echilibru ale puntii sunt:

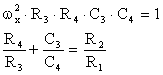
Daca se aleg: C₃=C₄=C; R₃=R₄=R; R₂=2R₁, conditia (7.12) este indeplinita si din relatia (7.11) rezulta frecventa de masurat:

Puntea Wien - Robinson asigura o precizie mai mare decat puntea de rezonanta deoarece nu contine bobine (care nu se pot realiza cu aceeasi precizie ca rezistoarele si condensatoarele).

Metoda de punte permite masurarea frecventelor cuprinse intre zeci de Hz si sute de KHz, cu precizii de ordinul 0,001.0,02%.

7.1.1.3. Metoda comparatiei

Aceasta metoda se bazeaza pe compararea frecventei de masurat cu frecventa data de o sursa etalon, folosind un osciloscop catodic.

Tensiunea de frecventa necunoscuta f_x se aplica placilor de deflexie pe orizontala (X) ale osciloscopului, iar placilor de deflexie pe verticala (Y) li se aplica tensiunea de frecventa cunoscuta f_c. Se considera faptul ca cele doua semnale sunt sinusoidale.

Daca raportul f_x/f_c este un numar rational de forma K₁/K₂, K₁ si K₂ fiind numere intregi fara divizor comun, pe ecranul osciloscopului se obtin curbe inchise, denumite figurile lui Lissajous.

Din forma curbei se poate deduce atat raportul frecventelor cat si defazajul dintre cele doua tensiuni. Pentru aceasta se numara punctele de intersectie ale curbei cu doua drepte, una orizontala si una verticala. Daca n_H si n_V sunt numerele respective, frecventa necunoscuta rezulta din relatia:

(7.14)

Cu ajutorul figurilor Lissajous se pot compara usor frecvente al caror raport este mai mic de 10. Utilizarea cea mai comoda a metodei se obtine in cazul egalitatilor celor doua frecvente, cand pe ecran apare o elipsa (care poate degenera intr-o dreapta, cand diferenta de faza dintre semnale este un numar intreg de p). Daca frecventele difera foarte putin, se obtine o elipsa mobila in jurul centrului sau. Timpul t in care elipsa efectueaza o rotatie completa este egal cu inversul diferentei celor 2 frecvente:

Cronometrand timpul t, se poate determina diferenta f_x-f_c.

7.1.2. Masurarea numerica a frecventei

Frecventmetrele numerice se bazeaza pe numararea unor impulsuri necunoscute intr-un interval de timp cunoscut.

Frecventa si timpul fiind doua marimi fizice care prin natura lor sunt strans legate intre ele, majoritatea aparatelor numerice destinate masurarii frecventei permit si masurarea unor marimi temporale (timpul, perioada, intervalele de timp, defazajele). In acest caz functionarea aparatului se bazeaza pe numararea unor impulsuri de frecventa cunoscuta intr-un interval de timp necunoscut.

Aparatul cu functiuni multiple, utilizat pentru masurarea frecventei, a raportului a doua frecvente, perioadei, unui multiplu de perioade, intervale de timp, etc., este denumit numarator universal sau frecventmetru multifunctional.

7.1.2.1. Functionarea in regim de frecventmetru

Schema de principiu a unui frecventmetru numeric (fig.7.8) contine urmatoarele blocuri functionale:

circuitul de intrare;

circuitul poarta (P);

baza de timp impreuna cu circuitele de control asociate;

blocul de numarare zecimala si afisare.

Fig. 7.8. Schema bloc a frecventmetrului numeric

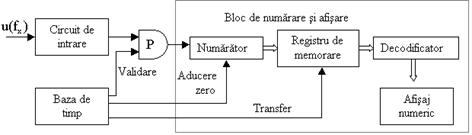
Circuitul de intrare are rolul de a converti semnalele de intrare (alternativ, impulsuri) intr-o forma compatibila cu logica interioara a aparatului si anume intr-o succesiune de impulsuri de nivel logic 0 si 1. Circuitul de intrare are in componenta sa un atenuator de intrare, un etaj de limitare a tensiunii cu diode Zener pentru protejarea circuitului, un amplificator de intrare care confera canalului o impedanta mare de intrare si o impedanta mica de iesire (realizat cu tranzistoare cu efect de camp), avand in acelasi timp un reglaj de nivel pentru alegerea punctului de basculare la tensiuni pozitive sau negative, precum si un Trigger Schmitt care transforma semnalul in impulsuri de nivele logice 0 si 1.

Circuitul poarta principala (P) este in general un circuit logic combinational cu doua intrari (de regula, o poarta SI): pe o intrare se aplica semnalul purtator de informatie, prelucrat in circuitul de intrare, iar pe cea de-a doua intrare (validare) se aplica semnalul de comanda provenit de la baza de timp a aparatului. Cat timp semnalul de comanda, de pe intrarea de validare, este la nivelul logic 1 (SUS), impulsurile provenite de la circuitul de intrare trec prin poarta catre blocul de numarare si afisare.

Baza de timp (BT) are rolul de a crea intervalul de masura, plecand de la un oscilator foarte stabil, urmat de un divizor de frecventa (realizat cu numaratoare decadice) care reduc frecventa de iesire a osciloscopului in trepte, prin divizare cu 10.

De regula, se asociaza bazei de timp si circuitele secventiatorului care genereaza semnalele de control necesare coordonarii operatiilor dintr-un ciclu de masurare.

Blocul de numarare si afisare (BNA) contine: numaratorul decadic propriu-zis, un registru de memorare a rezultatului numararii, decodificatorul si afisajul numeric. Registrul plasat intre numarator si decodificator are rolul de a stabiliza indicatia aparatului pentru a putea fi citita de catre operator. Pe durata masurarii (T_m), prescrisa de catre baza de timp, legatura cu blocul de afisare este intrerupta, in registru pastrandu-se valoarea masurata anterior. Astfel se asigura o afisare stabila, fara clipiri suparatoare. Dupa terminarea masuratorii, secventiatorul comanda inchiderea portii P, transferarea numarului memorat in registru catre blocul de afisare, precum si aducerea la zero a numaratorului, pregatind astfel aparatul pentru o noua secventa de masurare.

In fig. 7.9 este prezentata schema functionala simplificata a frecventmetrelor numerice. Baza de timp asigura impulsuri la intervale de timp foarte exacte, de perioada T_m=10^-n sec. Cu ajutorul comutatorului K se prescrie (manual) timpul de masura (T_m=1ms, 10m ms, .10s).

Bistabilul T plasat dupa comutatorul K, are rolul de a transforma perioada semnalului cules de la divizorul de frecventa (DF) al bazei de timp, intr-un impuls de durata egala cu a perioadei respective (T_m).

In intervalul de timp T_m, cat poarta P este deschisa, trec spre numarator N impulsuri de perioada T_m (frecventa f_x), adica:

(7.16)

sau

(7.17)

Relatia (7.17) reprezinta ecuatia de functionare a frecventmetrului numeric.

Daca se selecteaza T_m=1 sec, rezulta N=f_x, adica numarul afisat reprezinta frecventa in Hz.

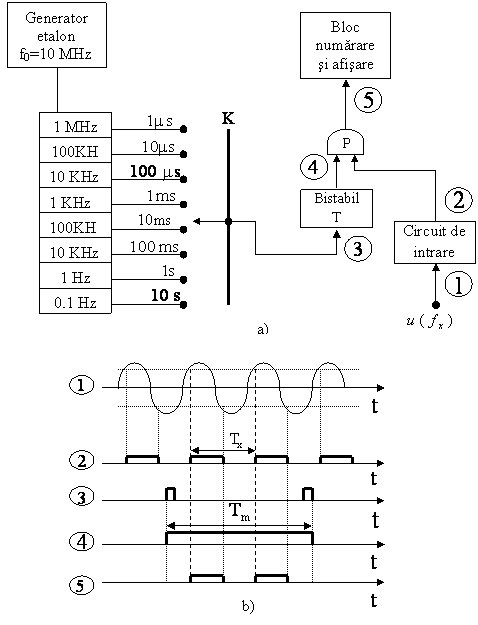
Fig. 7.9. Frecventmetrul numeric: a) schema functionala

b) diagramele semnalelor

Similar cu regimul de frecventmetru, aparatul poate functiona si in regim de totalizator; in acest caz inchiderea si deschiderea portii P se face din exterior (si nu din baza de timp interna), fie manual (un buton de START/STOP), fie cu doua semnale de comanda.

Din ecuatia de functionare (7.17) se deduce eroarea de masurare a frecventei:

(7.18)

unde    reprezinta eroarea etalonului de frecventa

(10^-6.10^-8), iar e_N DN/N este eroarea numaratorului.

Eroarea DN= 1 si se datoreaza faptului ca semnalul de intrare si cel al bazei de timp nu sunt sincronizate intre ele si ca urmare, ultimul impuls de numarat poate sa inceapa sau nu in intervalul T_m.

Deoarece DN= 1 (din cifra ultimului rang), adica cea mai mica variatie perceptibila la iesirea frecventmetrului, eroarea e 1/N reprezinta tocmai rezolutia aparatului.

Relatia (7.18) se poate scrie sub forma:

(7.19)

Din (7.19) rezulta ca eroarea e_fx este cu atat mai mica cu cat numarul afisat N este mai mare.

Daca e_N este de acelasi ordin cu e , rezulta ca e_fx=10^-6.10^-8, ceea ce arata ca frecventmetrul numeric este cel mai precis aparat de masurare. Pe de alta parte, pentru ca e_N £ e =10^-6.10^-8 este necesar ca N³10⁶.10⁸ si deci, pentru a pune in valoare inalta precizie a etalonului de frecventa trebuie ca numarul de cifre ale afisajului sa fie mai mare sau cel putin egal cu exponentul preciziei etalonului. De exemplu, daca etalonul are precizia e =10^-8, frecventmetrul trebuie sa aiba cel putin 8 cifre afisabile.

Din relatia (7.19) rezulta ca la micsorarea frecventei semnalului de intrare (f_x), eroarea e_fx creste, deoarece numarul de impulsuri contorizate (N) in intervalul T_m scade. De exemplu, pentru f_x=100 Hz si T_m=1s, N=100 si deci e_N=1%, ceea ce anuleaza inalta precizie a etalonului de frecventa. Pentru T_m=10s si f_x=100Hz rezulta N=1000 si e_N=1%. Micsorarea in continuare a erorii e_N, pe seama cresterii lui T_m nu este convenabila, deoarece aparatul devine prea lent. In asemenea situatii (frecvente joase), pentru micsorarea erorii e_N se recurge la masurarea perioadei T_x=1/f_x

7.1.2.2. Functionarea in regim de periodmetru

In schema bloc a periodmetrului (fig.7.10,a) se utilizeaza aceleasi elemente ca si la masurarea frecventei, cu observatia ca baza de timp si semnalul din circuitul de intrare isi inverseaza rolurile.

Semnalul de intrare cu frecventa de masurat f_x comanda, prin intermediul divizorului de frecventa al bazei de timp, durata de deschidere a portii P, prin care trec impulsuri de tact cu frecventa f₀ de la generatorul etalon (oscilator cu cuart). Deci ecuatia de functionare este:

(7.20)

Pentru a micsora eroarea numaratorului (e_N=1/N), se recurge la cresterea numarului de impulsuri contorizate N, prin selectarea mai multor perioade (nT_x), situatie in care ecuatia de functionare devine:

n T_x=N T₀ (7.21)

sau

Selectarea intervalului de masurare T_m=nT_x, se face cu ajutorul divizorului de frecventa conectat la iesirea circuitului de intrare. In acest fel, timpul de masurare T_m poate fi extins la 10T_x, 100T_x, ., nT_x, limita superioara (de obicei, 10 sec) fiind impusa de viteza de lucru a aparatului (numarului de masurari/sec).

Bistabilul T transforma semnalul de perioada nT_x, in impulsuri de durata T_m=nT_x (figura 7.10,b).

Ca si in regim de frecventmetru, precizia masurarii este data, in principal, de precizia generatorului etalon precum si de incertitudinea de numarare de 1 impuls. Eroarea de masurare a perioadei e_Tx se determina din (7.20):

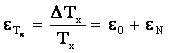unde: e DT₀/T₀ si e_N=1/N.

Fig. 7.10. Periodmetrul numeric: a) schema functionala

b)diagramele semnalelor

Din relatia (7.23) rezulta ca la frecvente joase (T_x mare) eroarea e_Tx poate fi mult mai mica decat la masurarea directa a frecventei f_x, deoarece numarul afisat N devine mult mai mare (7.20). De exemplu, pentru f_x=100 Hz (T_x=10 ms) si T₀=0,1 ms, rezulta N=10^-2/10^-7 si, deci,

e_N=1/N=10^-5. Daca T_m=10T_x sau 100T_x, e_N devine 10^-6, respectiv 10^-7, valori de acelasi ordin de marime cu e . Daca s-ar fi masurat direct frecventa, pentru f_x=100 Hz, s-ar fi obtinut (pentru T_m=1 s) N=100 si deci e_N=10^-2, valoare mult mai mare decat in cadrul perioadei T_x.

Daca frecventa f_x creste, avantajul periodmetrului fata de frecventmetru poate sa dispara. De exemplu, pentru f_x=10 KHz, T₀=10^-7s, e , in regim de periodmetru se obtine N=10^-4/10^-7=10³, e_N=10^-3, iar in regim de frecventmetru: e_N=1/10⁴=10^-4. Rezulta ca pentru frecvente de masurat f_x ridicate este mai avantajoasa masurarea directa a frecventei (regimul de frecventmetru).

7.1.2.3. Masurarea raportului a doua frecvente

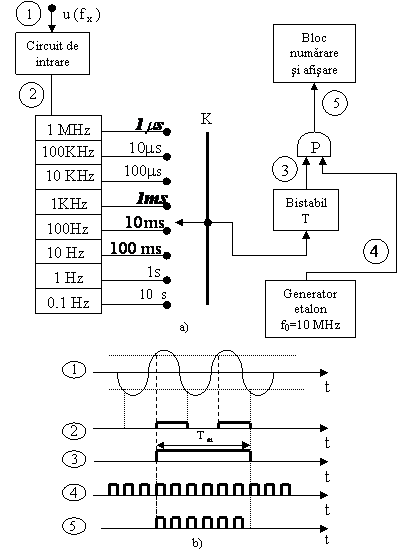
Masurarea unui raport de frecvente consta intr-o comparare a doua semnale de frecvente f₁ si f₂. Semnalul de frecventa mai mare (f₁>f₂), dupa formare, se aplica portii P, iar semnalul de frecventa mai mica (f₂), se utilizeaza ca baza de timp (fig. 7.11,a).

Din relatia:

rezulta ecuatia de functionare:

Ca si in cazul periodmetrului, n se alege astfel incat eroarea de numarare sa fie cat mai mica, la un timp de masurare rezonabil. Este evident ca acesta va fi cu atat mai mare cu cat frecventele f₁ si f₂ sunt mai apropiate.

7.1.2.4. Masurarea duratei impulsurilor

Masurarea duratei impulsurilor ori a distantei dintre acestea se poate face cu aparatul functionand intr-o schema similara cu cea de periodmetru (fig.7.12,a).

Durata unui impuls (t_i) reprezinta intervalul de timp dintre frontul ascendent (pozitiv) si cel descendent (negativ), luate la 50% din amplitudinea acestuia (fig.7.12,b si c).

Trecerea impulsului de masurat prin punctele A si B este sesizata de triggerul circuitului de intrare, care are rolul de formator. Acesta are atat iesire normala (+), cat si iesire inversata (-) pentru a permite

		a)

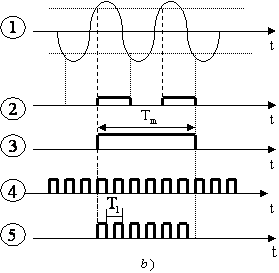
Fig. 7.11. Schema functionala pentru masurarea raportului a doua frecvente (a) si diagramele semnalelor (b).

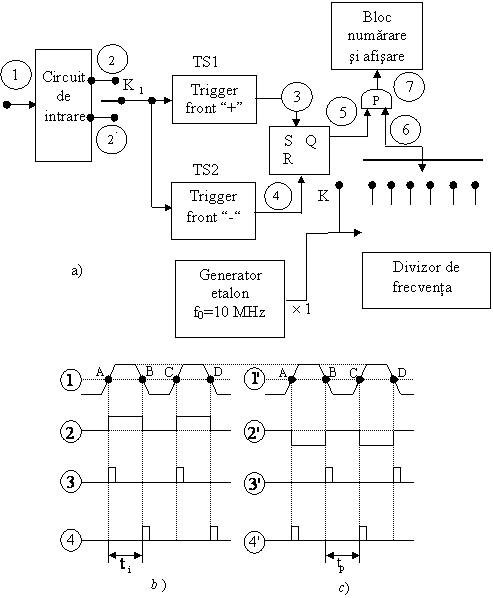Fig.7.12. Masurarea duratei si intervalului dintre impulsuri:

a)      schema functionala; b) si c) diagramele semnalelor.

comutatorului K alegerea modului de lucru: masurarea duratei sau masurarea distantei intre impulsuri (deoarece nivelul de declansare de 50% este valabil atat pentru evaluarea duratei cat si a distantei).

Masurarea duratei impulsurilor (t_i) se efectueaza in modul urmator: comutatorul K este pozitionat pe "+". Triggerele cu declansare pe front pozitiv, respectiv pe front negativ, emit cate un impuls scurt, distanta dintre acestea reprezentand tocmai durata t_i (fig.7.12, b). Cu aceste impulsuri se actioneaza bistabilul RS ce da la iesire un semnal de latime t_i, care comanda poarta P. Pe durata cat poarta este deschisa, spre numarator trec N impulsuri de perioada cunoscuta T₀ (furnizate de baza

de timp), deci t_i=NT₀, relatie din care rezulta ecuatia de functionare:

Masurarea intervalului dintre doua impulsuri consecutive (t_p) se face trecand comutatorul K in pozitia "-". In noua situatie triggerul TS1 declanseaza pe frontul descendent al primului impuls, iar TS2 pe frontul ascendent al urmatorului impuls, si ca urmare, distanta dintre impulsurile emise de TS1 si TS2 devine egala cu t_p (fig.7.12, c).

La iesirea bistabilului RS se obtine un semnal de latime t_p, care serveste la comanda portii P. In intervalul de timp (t_p) cand poarta P este deschisa, spre numarator trec N impulsuri de perioada T₀, adica t_p=NT₀ si deci:

(7.27)

7.2. Masurarea defazajului si a factorului de putere

Masurarea defazajului se poate face pe cale directa cu aparate specializate (fazmetre sau cosfimetre) sau aparate universale cu functii specifice (numarator industrial, osciloscop) si pe cale indirecta.

7.2.1. Masurarea indirecta a factorului de putere

Conform definitiei, in regim periodic permanent sinusoidal sau nesinusoidal, factorul de putere K_p este raportul dintre puterea activa si cea aparenta:

(7.28)

In regim sinusoidal factorul de putere se confunda cu cosinusul defazajului dintre tensiune si curent: K_p=cosj

In circuite monofazate cu o schema de masurare a puterii active cu un wattmetru, un voltmetru si un ampermetru, neglijand consumul propriu al aparatelor, factorul de putere rezulta:

(7.29)

Precizia metodei este limitata de neglijarea consumurilor proprii ale aparatelor si de erorile limita de masurare ale celor trei aparate.

In circuitele trifazate factorul de putere global se poate determina cu relatia (7.28). Daca circuitul trifazat este simetric, echilibrat cu trei conductoare, puterea activa fiind masurata cu metoda a doua wattmetre, factorul de putere se poate determina cu relatia:

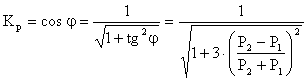
(7.30)

unde P₁ si P₂ sunt puterile indicate de cele doua wattmetre.

Metodele cu wattmetre permit determinarea factorului de putere la un moment dat. Factorul de putere mediu pe un interval de timp prezinta importanta in exploatarea instalatiilor electrice si se determina pe baza masurarii energiilor activa si reactiva consumate:

(7.31)

deci:

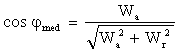
7.2.2. Masurarea directa a defazajului si a factorului de putere

Metoda indirecta nu se poate aplica decat in conditii de laborator sau pentru incercari de control. In conditii de exploatare curenta, defazajul si factorul de putere se masoara direct cu ajutorul aparatelor indicatoare numite fazmetre (sau cosfimetre).

7.2.2.1. Fazmetrul electrodinamic monofazat

Fazmetrul electrodinamic monofazat se realizeaza pe baza logometrului electrodinamic, avand bobina fixa montata in serie in circuit si bobinele mobile conectate in paralel in circuit (fig.7.13,a). In serie cu bobina mobila 1 este conectata o rezistenta R de valoare mare in comparatie cu reactanta circuitului respectiv, astfel incat curentul I₁ din aceasta bobina sa poata fi considerat in faza cu tensiunea U. In serie cu bobina mobila 2 este conectata o bobina de inductivitate L, avand reactanta inductiva mult mai mare decat rezistenta circuitului, astfel incat curentul I₂ din aceasta bobina sa poata fi considerat defazat cu 90 in urma tensiunii U (fig.7.13,b).

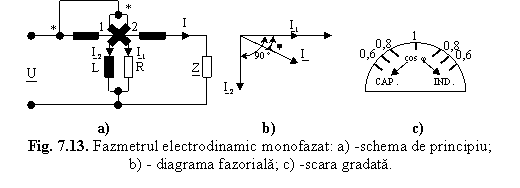
Tinand seama de diagrama fazoriala (fig.7.13,b) ecuatia de functionare a logometrului electrodinamic va fi:

. (7.33)

Daca impedantele bobinelor mobile sunt egale si R=wL, relatia (7.33) devine:

(7.34)

de unde

a j

Rezulta ca deviatia a este numeric egala cu valoarea defazajului.

Daca defazajul j devine negativ (sarcina capacitiva), deviatia isi schimba si ea sensul (a<0), de unde rezulta ca scara fazmetrului are 0 la mijloc (scara bilaterala) si o extindere pana la 180

Deoarece in practica, de regula, se lucreaza in regim sinusoidal, scara fundamentala se gradeaza in cosj, devenind in acest caz neuniforma (fig.7.13, c).

7.2.2.2. Fazmetrul electrodinamic trifazat

Fazmetrul trifazat se utilizeaza in circuite trifazate alimentate cu tensiuni simetrice si curenti echilibrati.

Din punct de vedere constructiv se aseamana cu fazmetrul monofazat, cu deosebirea ca unghiul dintre planele bobinelor mobile este de 120 , iar in serie cu aceste bobine sunt conectate rezistente de valori egale (fig.7.14.).

Bobina de curent se monteaza in serie cu una dintre faze; circuitele de tensiune sunt alimentate cu tensiuni intre faza respectiva si celelalte doua faze ale circuitului trifazat. Ecuatia de echilibru este: a j

Cosfimetrele electrodinamice pot functiona numai la frecvente nominale. Clasele de precizie sunt intre 0,5 si 2,5.

7.2.2.3. Fazmetrul electronic analogic

Functionarea fazmetrelor electronice analogice se bazeaza pe faptul ca valoarea medie a unui sir de impulsuri dreptunghiulare de amplitudine constanta este proportionala cu raportul dintre latimea impulsurilor si perioada lor.

Cele doua tensiuni, al caror defazaj se masoara, se aplica amplificatoarelor - limitatoare, la iesirile carora rezulta semnale dreptunghiulare, avand aceeasi amplitudine U₀ (fig.7.15) care se aplica amplificatorului diferential AO. La iesirea amplificatorului AO se obtine tensiunea:

. (7.36)

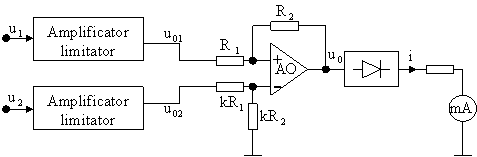
Fig. 7.15. Fazmetru electronic analogic.

Deoarece amplitudinile tensiunilor dreptunghiulare u^'₁si u^'₂ sunt egale, rezulta ca tensiunea u₀ va fi diferita de zero numai in intervalele cand ele au semne contrare (fig.7.16).

u_o=2ּ , t

u_o=0, t

Tensiunea u₀ este redresata si apoi aplicata unui instrument magnetoelectric, care masoara valoarea medie a curentului:

(7.37)

unde I₀ este o constanta a aparatului.

Rezulta ca indicatia instrumentului magnetoelectric este proportionala cu defazajul dintre cele doua tensiuni de la intrare.

Erorile de masurare depind de eroarea de detectie a zeroului, tensiunea de decalaj a AO, stabilitatea nivelului I₀ al curentului si eroarea instrumentala.

7.2.2.4. Fazmetre numerice

Defazajul dintre doua tensiuni de aceeasi frecventa: u₁=U_1msinwt, u₂=U_2msin(wt - j)=U_2msinw(t - t), poate fi exprimat prin relatia:

(7.38)

unde t reprezinta intervalul dintre trecerile consecutive prin zero a celor doua tensiuni (fig.7.16).

Deci, masurand t si cunoscand perioada T a semnalelor se poate determina defazajul j

In figura 7.17 este prezentata schema de principiu a unui fazmetru numeric.

Tensiunile u₁ si u₂ sunt mai intai formate (circuitele de intrare) si apoi aplicate la intrarile active pe front pozitiv ale celor doua monostabile care, in momentul cand tensiunile dreptunghiulare formate din u si u₂ ating 50% din amplitudine, emit cate un impuls scurt, distanta dintre impulsuri fiind t j w. Cand impulsul emis de monostabilul A ajunge la bistabilul RS, acesta basculeaza, iesirea lui trece in 1 logic si, ca urmare, poarta P se deschide, cand impulsul emis de monostabilul B ajunge la bistabilul RS, acesta revine in starea initiala si poarta P se inchide.

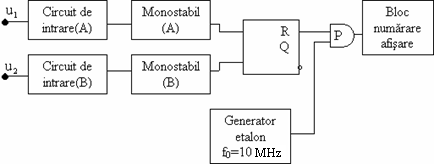
Fig. 7.17. Fazmetru numeric

In intervalul t, cat poarta a fost deschisa, spre numarator au trecut N impulsuri de perioada cunoscuta T₀ (furnizate de generatorul etalon), adica:

(7.39)

Din ecuatiile (7.38) si (7.39) rezulta ecuatia de functionare a fazmetrului numeric:

(7.40)

sau:

N=Kj (7.41 )

unde este constanta aparatului.

7.2.2.5. Masurarea defazajului cu osciloscopul

a. Metoda elipsei se bazeaza pe aplicarea celor doua marimi (tensiuni) intre care exista unghiul de defazaj j, pe intrarile Y, respectiv X ale osciloscopului (se utilizeaza intrarea X prin deconectarea bazei de timp):

(7.42)

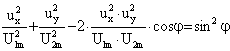Prin eliminarea timpului t, din relatiile (7.42) se obtine ecuatia unei elipse:

(7.43)

Se regleaza amplificarile pana cand elipsa se inscrie intr-un patrat (fig.7.18,a), astfel incat U_1m=U_2m=A si deci ecuatia (7.43) devine:

(7.44)

Fig. 7.18. Masurarea defazajului cu osciloscopul

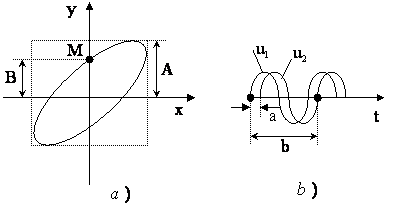Pentru x=0, se obtine:

Y_M=B=Asinj (7.45)

unde B reprezinta ordonata punctului M.

Masurand cele doua segmente A si B, se determina defazajul:

(7.46)

Sunt posibile urmatoarele cazuri particulare:

pentru j j , elipsa se transforma intr-o dreapta, y=x (prima bisectoare);

pentru j , ecuatia (7.44) devine y=-x (ecuatia celei de-a doua bisectoare);

pentru j j , elipsa se transforma intr-un cerc.

Aceasta metoda permite determinarea numai a valorii absolute a defazajului j, nu si a semnului acestuia.

De exemplu, pentru B/A=1/2, din (7.46) rezulta:

j=arcsin B/A=30 sau 330

Semnul defazajului j se poate determina introducand un defazaj suplimentar cunoscut, in canalul u_y si observand modul in care se modifica forma elipsei. Daca defazajul total a crescut, rezulta ca defazajul initial este de acelasi semn cu cel introdus suplimentar, iar daca defazajul total scade, defazajul initial si cel suplimentar sunt de semne contrare.

b. Utilizarea osciloscopului cu doua spoturi permite vizualizarea simultana pe ecran a doua tensiuni u₁ si u₂. Se regleaza si se deplaseaza curbele pana cand au aceeasi axa orizontala si aceeasi amplitudine. Se masoara segmentele a si b (fig.7.18, b) corespunzatoare defazajului si respectiv perioadei, defazajul fiind:

(7.47)

7.3. Masurarea factorului de distorsiune

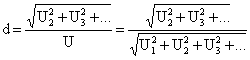
Abaterea unei tensiuni de la forma sinusoidala este caracterizata cu ajutorul factorului (sau coeficientului) de distorsiune, egal cu raportul dintre valoarea efectiva a armonicilor si valoarea efectiva a semnalului:

Se observa ca in expresia lui d nu intervine componenta continua U₀.

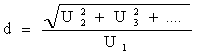
Daca d<<1, atunci se poate considera ca valoarea efectiva a semnalului este aproximativ egala cu valoarea efectiva a fundamentalei (U₁). In acest caz particular, factorul de distorsiune este:

Factorul de distorsiune este o masura a energiei armonicilor superioare in comparatie cu energia totala vehiculata de un semnal. El se mai numeste uneori si continut de armonici. Are avantajul ca poate fi exprimat si masurat simplu, constituind, cel mai des utilizat parametru global pentru caracterizarea abaterii unui semnal de la forma sinusoidala. El nu da insa nici o informatie asupra amplitudinii relative a armonicilor de diferite ordine si nici asupra fazelor lor.

7.3.1. Distorsiometre cu filtru

Principiul masurarii factorului de distorsiune al unui semnal se bazeaza pe separarea armonicilor din intregul semnal. Acest principiu (fig.7.19) utilizeaza un filtru care are rolul de a elimina fundamentala(de pulsatie . Voltmetrul V₁ de la intrare masoara valoarea efectiva a semnalului, in timp ce voltmetrul V₂ masoara valoarea efectiva a armonicilor, inmultita cu atenuarea introdusa de filtru pentru armonicile respective. Cunoscandu-se atenuarea a introdusa de filtru, si indicatiile celor doua voltmetre (U₁, U₂), factorul de distorsiune se determina, conform relatiei (7.48), cu relatia:

(7.49)

Fig. 7.19. Principiul de masurare a factorului de distorsiune

Principiul prezentat in figura 7.19 necesita efectuarea unui calcul pentru determinarea valorii factorului de distorsiune d, si este imprecis, deoarece implica utilizarea a doua voltmetre. Aceste inconveniente sunt eliminate in aparatele specializate, denumite distorsiometre cu filtru care permit citirea directa a valorii factorului de distorsiune.

Principiul de functionare este prezentat in figura 7.20.

Cu ajutorul comutatorului K, aparatul de masura (mV) poate fi conectat alternativ la intrare (K in pozitia 1) si dupa filtrul opreste banda (K in pozitia 2). Masurarea se efectueaza in doua etape. In prima etapa, comutatorul K se fixeaza in pozitia "1". Cu ajutorul potentiometrului P, nivelul semnalului de intrare este adus la o valoare prestabilita (acul indicator al mV se aduce in dreptul unui reper fix a de pe scara gradata). Aceasta valoare constanta (de referinta) este determinata de valoarea efectiva a semnalului (fundamentala + armonica).

Fig. 7.20. Principiul distorsiometrului cu filtru

In etapa a doua a masurarii, comutatorul K este trecut in pozitia "2". Voltmetrul masoara tensiunea:

(7.50)

unde K_V reprezinta constanta voltmetrului, iar a , indicatia acestuia.

Deoarece valoarea efectiva este U=K_Va , indicatia voltmetrului a in fiecare masurare concreta este proportionala cu factorul de distorsiune:

(7.51)

In consecinta scara milivoltmetrului poate fi gradata direct in valori ale factorului de distorsiune d.

Pentru eliminarea fundamentalei, distorsiometrele utilizeaza:

filtre trece - sus (FTS), care opresc complet si celelalte frecvente, mai mici decat fundamentala. FTS au avantajul de a opri si zgomotele de frecvente ale retelei sau dublul acesteia (induse, de exemplu, de redresorul distorsiometrului);

filtre opreste - banda (FOB), a caror frecventa de taiere se regleaza pe cea a fundamentalei.

7.4. Analiza si masurarea semnalelor modulate in amplitudine

Un semnal modulat in amplitudine (fig.7.21) se exprima prin relatia:

(7.52)

Unde w_p este pulsatia purtatoarei; w_m este pulsatia semnalului modulator; m - gradul de modulatie. Modulatia in amplitudine poate fi:

simetrica (semnalul de inalta frecventa este simetric fata de axa OX);

asimetrica (alternantele pozitive si negative ale semnalelor de pulsatie w_p difera intre ele ca amplitudine).

Gradul de modulatie al unui semnal modulat in amplitudine simetric se defineste astfel:

 

(7.53)

unde:

Fig. 7.21. Semnal modulat in amplitudine

a. Metoda directa de masurare a gradului de modulatie in amplitudine se bazeaza pe vizualizarea semnalului modulat pe ecranul unui osciloscop si determinarea marimilor A si B (fig. 7.21). Gradul de modulatie rezulta:

(7.55)

Metoda poate fi utilizata pentru semnalele modulate in amplitudine simetrice si pentru m<

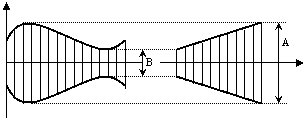
b. Metoda trapezului inlocuieste baza de timp a osciloscopului din metoda directa chiar cu semnalul modulator de pulsatie w_m. In acest mod, infasuratoarele superioara si inferioara vor fi proportionale in fiecare moment de timp cu semnalul aplicat placilor care introduc deflexia orizontala. Pe ecran apare un trapez (fig.7.22) ale carui laturi neparalele sunt rezultatul (in coordonate X - Y) infasuratoarei semnalului modulat (pe Y).

Fig. 7.22. Ilustrarea metodei trapezului

In cazul modulatiei in amplitudini simetrice, gradul de modulatie este dat de relatia (7.55).

c. Metoda dublei detectii se utilizeaza la aparatele care indica direct gradul de modulatie m. Aceste aparate sunt denumite modulometre. Principiul metodei consta in masurarea gradului de modulatie in amplitudine al unui semnal (fig.7.23,a) prin doua detectii. Dupa prima detectie, cea a semnalului de inalta frecventa (modulat), rezulta un semnal care reproduce infasuratoarea de modulatie (fig.7.23,b). Valoarea medie a semnalului este chiar amplitudinea purtatoarei U₀.

Cea de-a doua detectie conduce la separarea componentei alternative a infasuratoarei, care este proportionala cu mU₀, de componenta continua, determinata de U₀ (fig.7.23,c). Din raportarea celor doua valori masurate (U₀ si mU₀), rezulta gradul de modulatie m.

Schema simplificata a modulometrului este prezentata in fig.7.24,a. Conditia realizarii primei detectii este ca valoarea constantei de timp t=RC₁ sa fie mult mai mare decat perioada T_p (T_p=1/f_p) a purtatoarei si mult mai mica decat cea a semnalului modulator T_m (T_m=1/f_m).

Fig. 7.23. a) Semnalul modulat; b) semnalul dupa prima detectie;

c) semnalul dupa a doua detectie

Considerand separat grupul detector D-C₁-R (fig. 7.24,b) la intrarea caruia se aplica un semnal u(t) de forma (7.52), tensiunea u_R la bornele rezistorului R este:

(7.56)

unde r_d este rezistenta diodei D in conductie directa.

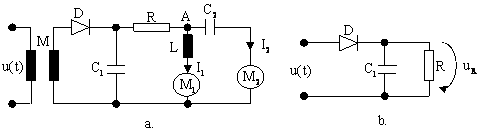
Fig. 7.24. Schema de principiu a modulometrului.

Notand cu: se observa ca expresia curentului

care apare dupa prima detectie in punctul A este:

(7.57)

Prezenta inductivitatii L determina trecerea prin instrumentul de masurare M₁ doar a componentei de curent continuu a semnalului

detectat de forma (7.57), proportionala cu U₀. Din raportarea indicatiilor instrumentelor M₁ si M₂, rezulta gradul de modulatie m.

Cuplajul M este variat astfel incat indicatia instrumentului M₁ sa aiba intotdeauna aceeasi valoare (de referinta) in fiecare masuratoare. In acest caz, scara instrumentului M₂ se gradeaza direct in valori ale gradului de modulatie m.