| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Campul magnetic in substante
a. Campul unei bucle de curent
b. Forta si momentul campului magnetic exercitate asupra unui dipol
c. Magnetizatia
d. Curentii moleculari
e. Relatia fundamentala a mediilor magnetice
f. Energia campului magnetic
g. Aplicatii
a. Campul unei bucle de curent
Fie cadrul dreptunghiular din figura 146. Presupunem ca acest cadru este strabatut de un curent de intensitate I in sensul aratat in figura.
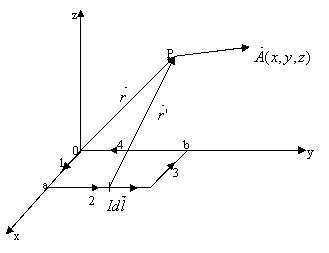
Fig. 146. Potentialul magnetic vector creat de un cadru strabatut de curent electric
Pornind de la relatia (III.31), in punctul P, de coordonate x,y,z, potentialul magnetic vector va fi:
![]()
unde ![]() si
si ![]() sunt versorii axelor
Ox si Oy, x' si y' sunt coordonatele punctului curent de pe circuit.
sunt versorii axelor
Ox si Oy, x' si y' sunt coordonatele punctului curent de pe circuit.
In practica intereseaza de multe ori campul magnetic creat de un cadru de curent intr-un punct situat la distanta mare de el. In aceste conditii sunt indeplinite inegalitatile:
![]()
si
x'/r<<1, y'/r<<1
Prin dezvoltare in serie Taylor a inversului marimii
![]()
Rezulta:
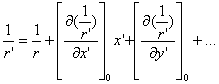
Oprindu-ne la termenii de ordin 1, obtinem:
1/r'≈1/r+x/r3∙x'+y/r3∙y'
Inlocuind in expresia potentialului se obtinem:
![]()
sau
![]()
Marimea: ![]() se numeste
momentul magnetic dipolar al cadrului.
se numeste
momentul magnetic dipolar al cadrului.
Tinand cont de orientarea vectorului ![]() , se poate defini vectorul moment magnetic dipolar prin
expresia:
, se poate defini vectorul moment magnetic dipolar prin
expresia:
![]()
In concluzie, potentialul vector produs de un cadru strabatut de curent electric la distanta mare de el este:
![]()
Curentul electric poate sa treaca printr-un conductor de forma arbitrara. In acest caz se poate afla moment magnetic procedand astfel: se inlocuieste bucla de curent cu o retea de ochiuri patrate infinitezimale; momentul magnetic fiind suma momentelor magnetice ale ochiurilor patrate infinitezimale.

Fig. 147. Referitor la calcularea momentului magnetic al unei bucle arbitrare de curent.
Pentru fiecare ochi avem:
![]()
unde:
![]()
Prin integrare obtinem:
![]() (III.34)
(III.34)
unde:
![]()
In sistemul International momentul magnetic se masoara in amperi ori metru patrat:
[m]S.I=1A∙m2 (III.35)
b. Forta si momentul campului magnetic exercitate asupra unui dipol
Dupa cum am aratat, lucrul mecanic elementar efectuat de un camp magnetic asupra unui circuit electric este:
![]()
Dezvoltand in serie inductia magnetica in jurul unui punct interior buclei de curent, rezulta:
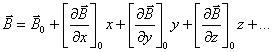
Presupunand variatia lui ![]() in interiorul
circuitului neglijabila, rezulta
in interiorul
circuitului neglijabila, rezulta
![]()
Cu aceasta aproximatie rezulta:
![]()
Lucrul mecanic elementar se va transcrie astfel:
![]()
Din definitia lucrului mecanic stim ca:
![]()
Comparand ultimele doua relatii, obtinem componentele fortei cu care actioneaza campul asupra curentului:
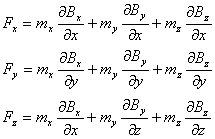
sau vectorial:
![]() (III.36)
(III.36)
Scriind forta Ampre sub forma (III.15) si alegand originea sistemului de coordonate in centrul buclei de curent, momentul fortei fata de acest punct va fi:
![]()
Distanta r este de acelasi ordin de marime ca lungimea l a buclei. Presupunem ca in interiorul buclei, ca si in situatia precedenta, inductia magnetica este practic constanta. In aceste conditii rezulta:
![]() (III.37)
(III.37)
Constatam ca rotatia buclei se produce pana cand momentul magnetic devine paralel cu campul.
c. Magnetizatia
Experienta arata
ca, daca o substanta se afla intr-un camp magnetic ea
capata un moment magnetic. Momentul magnetic total al unei probe se
noteaza cu ![]() . Momentul unitatii de volum se numeste
magnetizare si este dat, evident, de relatia:
. Momentul unitatii de volum se numeste
magnetizare si este dat, evident, de relatia:
![]() (III.38)
(III.38)
In Sistemul International unitatea de masura a magnetizari este amper/metru:
![]()
Magnetizarea este o functie de punct, fiind definita pe intregul volum al corpului.
Dupa cum am aratat, campul magnetic in vid, provine dintr-un potential vector. Se pune intrebarea, similara celei din electrostatica, cum se poate defini campul magnetic din interiorul substantei. Facand analogia cu situatia electrostatica, se admite ca in interiorul substantei, campul magnetic este produs de un potential vector ce este suma dintre potentialul vector produs de campul aplicat in absenta substantei si potentialul vector produs de catre substanta. Deci:
![]() (III.39)
(III.39)
unde: ![]() este potentialul
vector creat de curentii de conductie, dat de relatia (III.31),
iar
este potentialul
vector creat de curentii de conductie, dat de relatia (III.31),
iar![]() este dat de
relatia:
este dat de
relatia:
![]() (III.40)
(III.40)
si reprezinta potentialul vector creat de substanta magnetizata.
d. Curentii moleculari
Ampre a presupus ca magnetizarea substantei este produsa de niste curenti ciclici, microscopici, ce au fost numiti ulterior curenti moleculari sau amperieni.
Fie o suprafata foarte mica, la nivel macroscopic, inconjurata de curba Γ. Vom calcula circulatia magnetizarii in lungul curbei Γ.
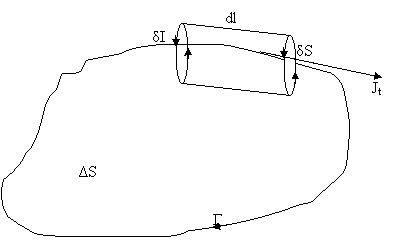
Fig. 148. Referitor la deducerea curentilor moleculari volumici.
Din fig. 148 rezulta
![]()
unde ![]() este componenta
tangentiala a lui
este componenta
tangentiala a lui ![]() la curba Γ.
la curba Γ.
Fie o suprafata, δs, perpendiculara pe ![]() . Membrul stang al relatiei de mai sus se transcrie
astfel:
. Membrul stang al relatiei de mai sus se transcrie
astfel:
![]()
Sa presupunem ca, prin conturul lui δs, trece curentul δI, relatia precedenta devine:
![]()
Marimea ΔIn este componenta normala a curentului ce trece prin suprafata Δs.
In analiza matematica, se
defineste rotorul unui camp vectorial ![]() , prin relatia:
, prin relatia:
![]()
Folosind aceasta definitie, rezulta:
![]()
sau, integral:
![]() (III.41)
(III.41)
Marimea ![]() este
densitatea volumica a curentilor moleculari.
este
densitatea volumica a curentilor moleculari.
La suprafata de separatie a doua medii magnetizate sau dintre un mediu magnetizat si vid apar curenti moleculari superficiali.
Fie, ca in figura 149, doua medii magnetizate ce se afla in contact.

Fig. 149. Referitor la deducerea curentilor moleculari superficiali.
Fluxul densitatii curentilor moleculari prin suprafata S este:
![]()
Membrul stang al acestei relatii se transcrie astfel:
![]()
unde ![]() este valoarea medie a
diferentei magnetizarilor in lungul laturilor
este valoarea medie a
diferentei magnetizarilor in lungul laturilor ![]() .
.
Membrul drept poate fi inlocuit cu:
![]()
unde ΔIm sup este componenta normala a curentului molecular prin suprafata S.
Tinand cont de cele spuse mai sus, putem afirma ca:
![]()
unde ![]() este componenta
tangentiala a curentilor moleculari superficiali.
este componenta
tangentiala a curentilor moleculari superficiali.
Pentru
ca ![]() sa reprezinte
chiar componenta normala a curentilor moleculari superficiali,
trebuie ca Δl sa tinda catre 0 (Δl este un infinit de
ordin superior in raport cu l). In aceste conditii rezulta ca:
sa reprezinte
chiar componenta normala a curentilor moleculari superficiali,
trebuie ca Δl sa tinda catre 0 (Δl este un infinit de
ordin superior in raport cu l). In aceste conditii rezulta ca:
![]()
Fie ![]() normala la
suprafata de separatie dintre cele doua medii, ca in figura 150.
Evident, marimea
normala la
suprafata de separatie dintre cele doua medii, ca in figura 150.
Evident, marimea ![]() , este componenta vectorului:
, este componenta vectorului:
![]() (III.42)
(III.42)
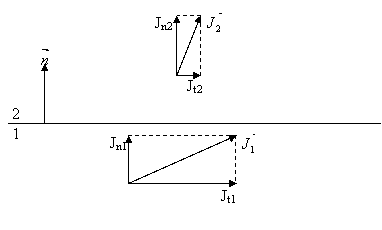
Fig.
150. Referitor la orientarea vectorului ![]()
Vectorul ![]() reprezinta tocmai
densitatea curentilor moleculari superficiali.
reprezinta tocmai
densitatea curentilor moleculari superficiali.
e. Relatia fundamentala a mediilor magnetice
In interiorul
unei substante magnetizate, densitatea de curent intr-un punct este sume
dintre densitatea curentilor de conductie, ![]() , si densitatea curentilor moleculari,
, si densitatea curentilor moleculari, ![]() . Folosind legea lui Ampre putem scrie:
. Folosind legea lui Ampre putem scrie:
![]()
Grupand termenii, relatia precedenta devine:
![]()
Marimea:
![]() (III.43)
(III.43)
se numeste intensitatea campului magnetic.
In sistemul international, intensitatea campului magnetic se masoara in amperi pe metru:
[H]SI=A/m.
Campul magnetic de intensitate 1 A/m este campul produs in centrul unei spire circulare de 1 metru diametru parcursa de un curent de 1 A.
Relatia de definitie a intensitatii campului magnetic (III.43) se numeste formula fundamentala a mediilor magnetice.
Se numesc medii magnetice perfecte, mediile in care
magnetizarea este proportionala cu ![]() (liniare), nu depinde
de orientarea lui
(liniare), nu depinde
de orientarea lui![]() (izotrope) si nu depinde de punct (omogene).
(izotrope) si nu depinde de punct (omogene).
In mediile magnetice perfecte relatia de legatura dintre magnetizare si intensitatea campului magnetic este:
![]() (III.44)
(III.44)
unde χ este susceptivitatea magnetica a mediului.
Folosind relatia (III.44), relatia (III.43) devine:
![]()
marimea:
![]()
se numeste permitivitatea magnetica a mediului.
Se constata ca in mediile magnetice ideale legile magnetostaticii au aceeasi forma ca in vid. Deci, vidul poate fi considerat un mediu magnetic perfect.
Fie o suprafata de separatie dintre doua medii magnetice, ca in figura 151.
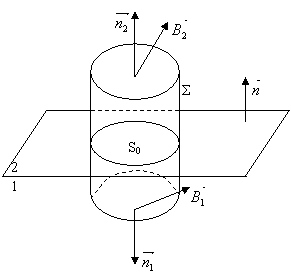
Fig.151. Discontinuitatea lui
![]() la suprafata de separatie a doua medii.
la suprafata de separatie a doua medii.
Pornind de la relatia (III.27), pe suprafata Σ, fluxul inductiei magnetice este:
![]()
Presupunand suprafetele S1 si S2
foarte mici, ![]() este constant pe ele
si deci:
este constant pe ele
si deci:
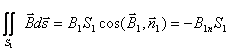
![]()
unde:
![]()
In mod analog:
![]()
Integrala pe suprafata laterala a cilindrului este:
![]()
unde <B> este media inductiei magnetice pe suprafata laterala a cilindrului.
Tinand cont de cele afirmate mai sus, rezulta ca:
![]()
Daca inaltimea cilindrului tinde catre 0, rezulta ca suprafata laterala tinde si ea spre 0 si deci:
![]()
Cum S0 este diferit de 0, se obtine:
B2n=B1n (III.45)
Presupunand ca cele doua medii magnetice sunt liniare, rezulta:
![]()
Deci, componenta normala a vectorului intensitate a campului magnetic are o discontinuitate la suprafata de separatie a doua medii magnetice.
Fie o curba Γ ce este normala pe suprafata de separatie a celor doua medii magnetice, ca in figura 15
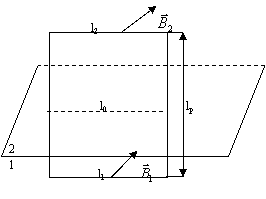
Fig.152. Referitor la circulatia vectorului ![]() la suprafata de separatie intre doua medii
magnetice.
la suprafata de separatie intre doua medii
magnetice.
Pornind de la relatia (III.26) si presupunand cele doua medii liniare, rezulta:
![]()
Presupunand l1 si l2 foarte mici, campul magnetic poate fi considerat constant in lungul lor si deci:
![]()
Daca lp este un infinit mic de ordin superior in raport cu l0, rezulta:
![]()
sau
![]() (III.46)
(III.46)
unde is este densitatea curentului superficial in directia perpendiculara pe componentele tangentiale ale campului.
In cazul in care is=0, rezulta:
![]() (III.47)
(III.47)
Deci, componenta tangentiala a campului magnetic este constanta la suprafata de separatie a doua medii magnetice.
f. Energia campului magnetic
Fie un tor dintr-o substanta magnetica in jurul caruia s-a infasurat o bobina, ca in figura 15
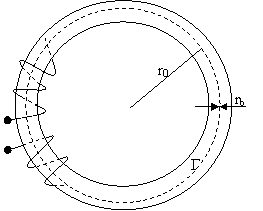
Fig. 15 Referitor la deducerea energiei inmagazinata in campul magnetic.
Presupunem ca ra>>rb. Pe curba Γ, circulatia intensitatii magnetice este:
![]()
unde N este numarul de spire ale bobinei. Din relatia precedenta rezulta:
![]()
Fluxul magnetic prin bobina va fi:
![]()
Diferentiind relatia precedenta rezulta:
![]()
Folosind relatia (III.21) rezulta energia totala transferata campului magnetic:
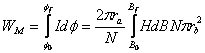
sau
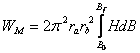
densitatea volumica a energiei magnetice este:
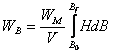
Evident, daca B0=0 si Bf =B iar mediul este perfect, rezulta:
![]() (III.45)
(III.45)
Aceasta relatie este valabila in orice regiune din spatiu in care exista camp magnetic.
g. Aplicatii
Problema 1
Se da sfera polarizata magnetic, uniform si permanent, cu magnetizarea J. Axa magnetica a sferei este dirijata de-lungul unui camp magnetic exterior, de intensitate H0 uniform. Sa se gaseasca lucrul mecanic necesar pentru a roti sfera magnetizata cu 180˚ in jurul unui diametru normal pe axa sa magnetica, in ipoteza ca polarizarea sferei nu se modifica.
Sfera magnetizata poate fi echivalenta cu un moment magnetic:
![]()
v fiind volumul sferei iar a raza ei.
Momentul care se exercita din partea campului exterior asupra sferei rotite din pozitia initiala cu unghiul θ va fi:
![]()
iar lucrul mecanic necesar rotirii cu un unghi elementar dθ va fi:
![]()
In consecinta, pentru o rotatie de 180˚:
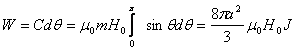
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1619
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved