CIRCUIT RAMIFICAT DE CURENT CONTINUU DE ENERGIE CONECTATE IN RAMURI DIFERITE

1 Principiul superpozitiei curentilor

Aplicatie practica.

Pentru circuitul din fig. 3.1 sa se determine curentii in toate portiunile de circuit si tensiunile intre nodurile A, B si C pentru urmatoarele date: R₁ = R₃ = 2 Ω; R₂ = 1,6 Ω; E₁ = 3,6 V; E₂ = 4,8 V; r₀₁ = r₀₂ = 0,5 Ω.

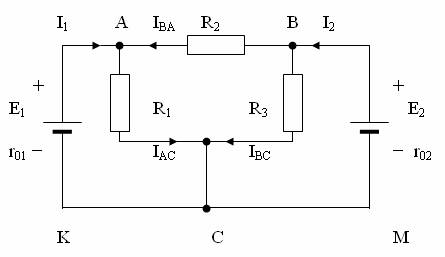
Fig. 3.1. Circuit complex continand doua surse de energie.

Rezolvarea problemei.

1. Aplicarea principiului superpozitiei curentilor pentru curentul din fig. 3.1. Circuitele ramificate formate din mai multe surse de energie, amplasata in ramuri diferite, ca in fig. 3.1, se numesc circuite complexe. Pentru calcularea unui astfel de circuit complex exista mai multe metode, dintre care una, principiul superpozitiei, se va examina in acest paragraf, celelalte metode constituind subiectul paragrafelor urmatoare.

Conform principiului superpozitiei, numit cateodata si principiul suprapunerii efectelor, curentul intr-o latura oarecare a circuitului poate fi considerat ca suma algebrica a curentilor produsi in acea latura de fiecare sursa in parte. Curentii produsi de fiecare sursa se numesc curenti partiali. Prima data se determina curentii partiali, pentru problema de aici ai sursei E₁ in absenta sursei E₂, adica se calculeaza circuitul simplu din fig. 3.2, dupa care se determina curentii partiali produsi de sursa E₂ neluand in considerare sursa E₁, adica se calculeaza circuitul simplu din fig. 3.3, dupa care se aduna algebric curentii partiali din cele doua cazuri.

Astfel, principiul superpozitiei permite inlocuirea calcului unui circuit continand mai multe surse de energie prin calculul mai multor circuite formate numai dintr-o singura sursa de energie.

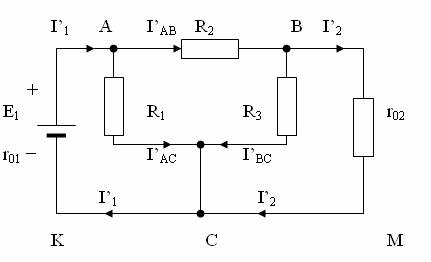
Fig. 3.2. Eliminarea sursei E₂ din circuitul complex din fig. 3.1.

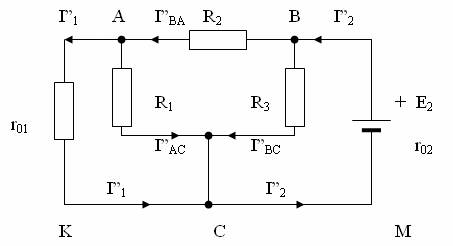
Fig. 3.3. Eliminarea sursei E₁ din circuitul complex din fig. 3.1.

2. Notarea curentilor partiali. Toti curentii partiali produsi de sursa E₁ (fig. 3.2) se noteaza cu litera I urmata de indicele prim (I`) si toti curentii partiali produsi de sursa E₂ prin indicele secund (I") (fig. 3.3).

3. Calculul curentilor partiali. Pentru circuitul format numai din sursa E₁ (fig. 3.2) se calculeaza, mai intai rezistenta echivalenta.

Astfel rezistenta portiunii BC:

R₃ · r₀₂ 2 · 0,5

R'_BC = ─────── = ────── = 0,4 Ω

R₃ + r₀₂ 2 + 0,5

Rezistenta portiunii BC este conectata in serie cu rezistenta R₂, deci:

R'_ABC = R₂ + R'_BC = 1,6 + 0,4 = 2 Ω

Se obtin astfel doua rezistente identice R'_ABC si R₁ conectate in paralel, din care cauza rezistenta echivalenta a circuitului exterior sursei E₁ este:

R R'_ABC 2

R'_AC = ──── = ───── = ─── = 1

2 2 2

Curentul de la sursa E₁ este:

E₁ 3,6

I'₁ = ──────── = ──── = 2,4 A

R₀₁ + R'_AC 1,5

Curentul partial I'₁ se imparte in nodul A in doi curenti identici:

I'₁ 2,4

I'_AB = I'_AC = ───── = ──── = 1,2 A

2 2

In nodul B curentul I'_AB se divizeaza in curentii I'₂ si I'_BC:

R₃ 2

I'₂ = I'_AB ────── = 0,96 A;

r₀₂ + R₃ 0,5 + 2

I'_BC = I'_AB - I'₂ = 1,2 - 0,96 = 0,24 A

Pentru circuitul al doilea, care contine numai sursa E₂, (fig. 3-3), se obtine:

R₁ r₀₁ 2

R"_AC = ─────── = ────── = 0,4

R₁ + r₀₁ 2 + 0,5

R"_BA = R₂ + R"_AC = 1,6 + 0,4 = 2

R"_BAC

R"_BC = ────── = ─── = 1 pentru ca R₃ = R"_BAC.

2 2

In latura de circuit care contine sursa E₂, circuitul partial este:

E₂ 4,8

I"₂ = ──────── = ──── = 3,2 A.

R"_BC + r₀₂ 1,5

Din cauza ca R"_BAC = R₃ = 2 rezulta ca:

I"₂ 3,2

I"_BA = I"_BC = ───── = ─── = 1,6 A.

2 2

Curentii prin portiunile de circuit conectate in paralel cuprinse intre nodul AC sunt:

R₁ 2

I"₁ = I"_BA · ─────── = 1,6 · ────── = 1,28 A ;

r₀₁ + R₁    2,5

I"_AB = I"_BA - I"₁ = 1,6 - 1,28 = 0,32 A

Calculul curentilor pentru circuitul complex din fig. 3-1. Curentii prin laturile de circuit se obtin prin insumarea algebrica a curentilor partiali din latura respectiva.

Pentru latura CKA, curentul partial I'₁(fig. 3-2) este orientat de la nodul C inspre nodul A si curentul partial I"₁ (fig. 3-3) dinspre nodul A catre nodul C, adica in sens opus cu primul curent partial. Curentul total prin latura CKA fiind:

I₁ = I'₁ - I" ₁ = 2,4 - 1,28 = 1,12 A

Sensul curentului I₁ (fig. 3-1) coincide cu sensul celui mai mare curent partial, in cazul de aici cu sensul curentului I'₁.

La fel se determina si curentii I_BA si I₂:

I_BA = I"_BA - I'_AB = 1,6 - 1,2 = 0,4 A ;

I₂ = I" ₂ - I'₂ = 3,2 - 0,96 = 2,24 A.

Directia curentilor I_BA si I₂ (fig. 3-1) coincide cu directia curentilor I" _BA respectiv I" ₂.

Pentru latura AC, cei doi curenti partiali I'_AC si I" _AC au acelasi sens, deci:

I_AC = I'_AC + I" _AC = 1,2 + 0,32 = 1,52 A.

La fel si pentru latura BC:

I_BC = I'_BC + I" _BC = 0,24 + 1,6 = 1,84 A.

5. Calculul tensiunilor. Tensiunile intre noduri sunt:

U_BA = I_BA · R₂ = 0,4 · 1,6 = 0,64 V;

U_AC = I_AC · R₁ = 1,52 · 2 = 3,04 V;

U_BC = I_BC · R₃ = 1,84 · 2 = 3,68 V.

6. Verificarea rezultatelor obtinute. Verificare se face utilizand teoremele lui Kirchhoff:

Pentru nodul A:

I_AC = I₁ + I_BA

In adevar:

1,52 = 1,12 + 0,

Pentru nodul B:

I₂ = I_BA + I_BC

In adevar:

2,24 = 0,4 + 1,84

Pentru conturul din circuitul ABC:

U_AC - U_CB + U_BA = 0

In adevar:

conturul stabilindu-se in sens antiorar.

2. METODA ECUATIILOR LUI KIRCHHOFF

Aplicatie practica.

Fie circuitul din fig. 3-4, in care E₁ = 60 V; E₂ = 48 V; E₃ = 6 V; R₁ = 200 Ω R₂ = 160 Ω; R₃ =10 Ω.Sa se determine curentii prin toate laturile de curent:

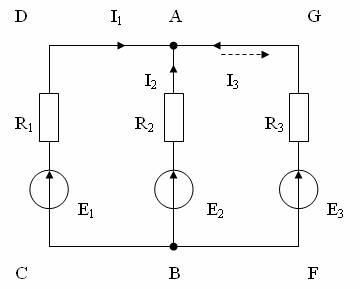
Fig. 3. Circuit complex cu trei laturi.

Rezolvarea problemei

1. Principiul metodei. Aceasta metoda se bazeaza pe aplicarea primei si celei de a doua teoreme a lui Kirchhoff, care nu necesita transfigurarea schemei si este aplicabila pentru orice circuit, fapt care constituie principalul ei avantaj.

Cate ecuatii trebuiesc scrise pentru rezolvarea circuitului? Este evident ca numarul de ecuatii trebuie sa fie egal cu numarul de necunoscute, in cazul acestei probleme, cu numarul curentilor. Rezolvarea problemei trebuie, deci, sa inceapa cu determinarea numarului de curenti necunoscuti.

2. Determinarea numarului de curenti necunoscuti si alegerea sensului acestor curenti. In fiecare portiune de circuit neramificat (latura) curentul are aceeasi valoare de la inceputul si pana la sfarsitul ei. Pentru circuitul examinat (fig. 3.4) in nodurile A si B sunt conectate trei portiuni de circuit (laturi): BCDA prin care curentul este I₁, BA cu curentul I₂ si BFGA avand curentul I₃.

Astfel, numarul de curenti diferiti este egal cu numarul laturilor circuitului electric.

Cum se aleg sensurile curentilor? Se stie ca pentru un circuit complex este imposibil de determinat sensurile tuturor curentilor, fara a se calcula, in prealabil, circuitul. Se incepe, deci, prin alegerea, in mod arbitrar, a sensurilor curentilor (a sensurilor pozitive ale curentilor); dupa aceea pentru sensurile alese se stabilesc ecuatiile. Dupa rezolvarea acestor ecuatii se gasesc sensurile efective ale curentilor dupa sensul lor algebric, astfel: curentii a caror sensuri efective sunt opuse sensurilor alese initial sunt exprimate prin numere negative.

Astfel, pentru prezentul caz, se poate sustine inca inainte de calcularea circuitului ca nu toate sensurile alese (notate prin sageti in fig. 3.4) coincid cu sensurile reale (efective) pentru ca este evident faptul ca toti curentii nu pot fi dirijati spre nodul A.

In concluzie, curentii din ecuatiile lui Kirchhoff sunt marimi algebrice a caror semne depind de sensul curentilor.

3. Stabilirea ecuatiilor dupa teoremele lui Kirchhoff. Pentru problema de aici exista trei curenti necunoscuti I₁, I₂ si I₃, iar pentru determinarea lor este necesar sa se stabileasca trei ecuatii.

Se incepe prin aplicarea primei teoreme a lui Kirchhoff. Pentru un circuit care are n noduri se pot stabili un numar (n-1) de ecuatii independente; pentru un nod oarecare al circuitului nu mai este necesara scrierea ecuatiei pentru ca aceasta rezulta din ecuatiile precedente.

Circuitul din fig. 3.4 are doua noduri A si B. Scriind, deci, o singura ecuatie, cu prima teorema a lui Kirchhoff, de exemplu, pentru nodul A, avem:

I₁ + I₂ + I₃ = 0 (3.1)

Celelalte doua ecuatii cautate se scriu dupa teorema a doua a lui Kirchhoff, de exemplu, pentru ochiurile de circuit BAGFB si CDGFC, (pentru ca ecuatiile sa fie independente, fiecare ochi trebuie sa contina fata de ochiul precedent o latura de circuit in plus).

Parcurgand fiecare ochi in sens orar si tinand seama de regula semnelor (v. discutia suplimentara 3 din paragraful 2-1) se obtine:

R₂· I₂ - R₃· I₃ = E₂ - E₃ (3.2)

R₁· I₁ - R₃· I₃ = E₁ - E₃ (3.3)

Calculul curentilor. Inlocuind in ecuatiile (3.2) si (3.3) valorile rezistentelor si valorile t.e.m. se obtine:

100 · I₂ - 10 · I₃ = 48 - 6

sau

100 · I₂ - 10 · I₃ = 42 (3.4)

200 · I₁ - 10 · I₃ = 54 (3.5)

Astfel, calculul curentilor se reduce la rezolvarea unui sistem de trei ecuatii (3.1), (3.4) si (3-5) cu trei necunoscute. Scotand curentul I₂ din ecuatia (3-1) si introducand valoarea sa in ecuatia (3.4):

- 100 · (I₁ + I₃) - 10 · I₃ = 42

reducand termenii asemenea se obtine:

- 100 · I₁ - 110 · I₃ = 42 (3.6)

S-au obtinut, astfel, doua ecuatii (3.5) si (3.6) cu doua necunoscute I₁ si I₃.

Inmultind ecuatia (3.6) cu 2 si adunand rezultatul, termen cu termen cu ecuatia (3.5) se obtine:

10 · I₃ - 220 · I₃ = 138,

de unde rezulta curentul

138

I₃ = - ───── = - 0,6 A.

230

Inlocuind valoarea curentului I₃ in ecuatia (3.6) se obtine ca:

- 100 · I₁ - 100 · (- 0,6) = 42

de unde:

I₁ = ───── = 0,24 A

Curentul I₂ se determina din ecuatia (3.1)

I₂ = - I₁ - I₃ = - 0,24 + 0,6 = 0,36 A

Curentii I₁ si I₂ au valori pozitive si I₃ valoare negativa, in consecinta, sensul primilor doi curenti a fost ales in mod corespunzator, in timp ce curentul I₃ nu. Sensul real (efectiv) al curentului I₃ este reprezentat printr-o sageata punctata in fig. 3. Suma curentilor I₁ + I₂ = 0,24 + 0,36 = 0,6 A este curentul I₃ si care are sensul real din nodul A inspre nodul B pa latura AGFB.

3 METODA CURENTILOR CICLICI (OCHIURILOR INDEPENDENTE)

Aplicatie practica.

Pentru circuitul din fig. 3.5, care s-a calculat in paragraful precedent prin metoda ecuatiilor lui Kirchhoff, sa se determine toti curentii pentru aceleasi date prin metoda curentilor ciclici.

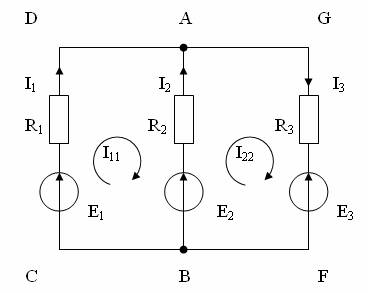
Fig. 3.5. Curentii de contur ai unui circuit cu trei laturi.

Rezolvarea problemei.

1. Curentii de contur (ciclici) si legatura lor cu curentii laturilor. Metoda curentilor ciclici se bazeaza pe utilizarea numai celei de a doua teoreme a lui Kirchhoff, ceea ce permite micsorarea numarului de curenti de rezolvat.

Pentru aceasta, se imparte schema in ochiuri (contururi independente) si se introduce pentru fiecare ochi (contur) curentul sau de contur, marime care, necunoscuta fiind, trebuie calculata.

Astfel, pentru circuitul dat, fig. 3.5, se pot realiza doua ochiuri, DABCD SI AGFBA si prin aceste contururi trec curentii ciclici I₁₁ si I₂₂.

Din schema se observa ca pentru laturile exterioare, DC si GF curentii de contur coincid cu curentii prin laturi, adica I₁ = I₁₁ si I₃ = I₂₂. Pentru latura din mijloc, portiunea de circuit AB din fig. 3.5, curentul I₂ al laturii este determinat de diferenta curentilor ciclici, adica I₂ = I₂₂ - I₁₁, tinandu-se seama ca pentru problema de aici, curentul I₂ este dirijat in acelasi sens cu curentul I₂₂ si are sens opus curentului I₁₁. In consecinta, pentru problema data, doi curenti de contur permit calcularea curentilor din trei laturi de circuit.

2. Determinarea rezistentelor proprii si comune a contururilor. Suma tuturor rezistentelor unui contur se numeste rezistenta proprie a conturului, astfel, pentru conturul DABCD (fig. 3.5) rezistenta proprie este:

R₁₁ = R₁ + R₂ = 200 + 100 = 300 Ω

si pentru conturul AGFBA:

R₂₂ = R₂ + R₃ = 100 + 10 = 110 Ω

Rezistenta unei laturi comune pentru doua contururi, ca latura AB din fig. 3-5 se numeste rezistenta comuna. Ea se noteaza cu R₁₂ pentru primul contur si pentru al doilea contur cu R₂₁. Observand ca R₁₂ si R₂₁ reprezinta rezistenta aceleasi laturi de circuit, este evident ca R₁₂ = R₂₁. Pentru cazul de aici R₁₂ = R₂₁ = R₂ = 100 Ω

3. Stabilirea ecuatiilor de contur si calculul curentilor. Scrierea ecuatiilor de contur se face dupa a doua teorema a lui Kirchhoff, pentru conturul BCDAB:

R₁ · I₁₁ - R₂ · (I₂₂ - I₁₁) = E₁ - E₂

sau grupand termeni care contin curentii I₁₁ si I₂₂ se obtine:

(R₁ + R₂) · I₁₁ - R₂ · I₂₂ = E₁ - E₂.

In mod analog se stabileste si ecuatia pentru conturul AGFBA:

R₂₂ · I₂₂ - R₂₁ · I₁₁ = E₂ - E₃.

Inlocuind valorile rezistentelor si a t.e.m. se obtine:

300 · I₁₁ - 100 · I₂ = 60 - 48 = 12 ;

110 · I₂₂ - 100 · I₁₁ = 48 - 6 = 42.

Astfel, calculul curentilor de contur I₁₁ si I₂₂ se reduce la rezolvarea unui sistem de doua ecuatii.

Inmultind cea de a doua ecuatie cu 3 si adunand-o, membru cu membru cu prima ecuatie se obtine:

300 · I₁₁ - 100 · I₂₂ + 330 · I₂₂ - 300 · I₁₁ = 12 + 126

de unde, dupa reducerea termenilor asemenea:

230 · I₂₂ = 138

sau:

I₂₂ = 138/230 = 0,6 A.

Inlocuind aceasta valoare in prima ecuatie de contur se obtine curentul I₁₁:

I₁₁= (1₂ + 100 · I₂₂) · 300 = (12+ 100*0,6) · 300 = 0,24 A.

Folosind legatura stabilita mai inainte (punctul 1) intre curentii ciclici si curentii reali se obtin valorile curentilor prin laturile de circuit:

I₁ = I₁₁ = 0,24 A

I₃ = I₂₂ = 0,6 A

I₂ = I₂₂ - I₁₁ = 0,6 - 0,24 = 0,36 A.

4 METODA CELOR DOUA NODURI.

Enuntul problemei

Doua generatoare conectate in paralel, fig. 3-7, cu t.e.m. E₁ = E₂ = 230 V si de rezistente interne r₁ = 0,5 Ω si r₂ = 0,4 Ω alimenteaza un receptor a carui rezistenta echivalenta R = 10 Ω.

Sa se determine toti curentii, puterile generatoarelor, pierderile de puteri pe rezistentele interne precum si puterea receptorului R.

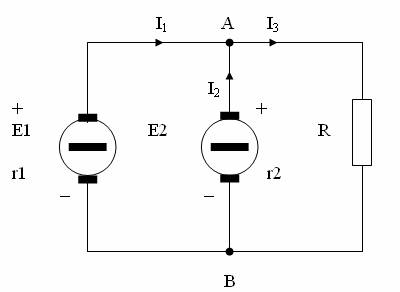
Fig. 3.7. Functionarea in paralel a doua generatoare.

Rezolvarea problemei.

1. Aplicarea metodei celor doua noduri. Spre deosebire de metoda curentilor ciclici, care se poate aplica pentru rezolvarea oricarui circuit, metoda celor doua noduri nu poate fi aplicata decat pentru calculul circuitelor care au numai doua noduri, fiind indiferent numarul de laturi.

In practica se intalnesc des circuite numai cu doua noduri si aceasta metoda simplifica, in mod considerabil, calculele.

Pentru calcul se foloseste formula urmatoare, care determina tensiunea intre cele doua noduri:

∑EG

U₀ = ────

∑G

unde:

∑EG este suma algebrica a produselor t.e.m. prin conductanta corespunzatoare,

∑G este suma conductantelor laturilor.

Atunci, prin circuitul considerat, fig. 3-7,

E₁ · G₁ + E₂ · G₂

U₀ = U_AB = ───────────── ·

G₁ + G₂ + G₃

In cazul de aici termenul E₃ · G₃ lipseste, pentru ca, in latura a treia nu exista t.e.m. Daca, de exemplu, t.e.m. E₂ ar avea sens opus, atunci inaintea termenului E₂ · G₂ trebuia sa se puna semnul minus.

2. Calculul tensiunii dintre noduri. Mai intai se determina conductanta fiecarei ramuri:

G₁ = ───── = ───── = 2 S;

r₁ 0,5

G₂ = ───── = ───── = 2,5 S;

r₂ 0,4

G = ───── = ───── = 0,1 S.

R 10

Astfel, tensiunea dintre cele doua noduri este:

E₁ G₁ + E₂ G₂ 230

U_AB = ────────── = ──────────── = 225 V.

G₁ + G₂ + G₃ 2 + 2,5 + 0,1

3. Alegerea sensurilor pozitive pentru curenti. Circuitul considerat (fig. 3-7) este format din trei laturi de circuit prin care trec curentii corespunzatori I₁, I₂ si I₃, curenti a caror sensuri, inaintea calcului circuitului sunt necunoscute, circuitul fiind complex; va trebui, deci, sa se aleaga sensurile pozitive in mod arbitrar, ca in fig. 3-7, reprezentati prin sageti.

Calculul curentilor. Sensurile curentilor, adoptate in fig. 3.7, coincid cu sensul t.e.m. In acest caz tensiunea dintre noduri sau tensiunea la capetele laturii, este egala cu diferenta dintre t.e.m. a sursei si caderea de tensiune pe rezistenta ramurii, adica:

U_AB = E₁ - I₁ · r₁ = E₂ - I₂ · r₂

de unde:

E₁ - U_AB

I₁ = ─────── = (E₁ - U_AB) · G₁ = (230 - 225) · 2 = 10 A.

r₁

E₂ - U_AB

I₂ = ─────── = (E₂ - U_AB) · G₂ = (230 - 225) · 2 =12,5 A.

r₂

Dupa legea lui Ohm, curentul I este:

U_AB

I = ───── = U_AB · G = 225 · 0,1 = 22,5 A.

R

5. Calculul puterilor. Puterile debitate de surse sunt:

P₁ = E₁ · I₁ = 230 · 10 = 2,3 Kw ;

P₂ = E₂ · I₂ = 230 · 12,5 = 2,875 kW.

Pierderile de putere pe rezistentele interne sunt:

P₀₁ = r₁ · I₁² = 0,5 · 10² = 50 W = 0,05 kW ;

P₀₂ = r₂ · I₂² = 0,4 · 12,5² = 62,5 W = 0,0625 kW.

Puterea consumatorului este:

P = R · I² = 10 · 22,5² = 5,0625 kW.

Stabilirea bilantului puterilor:

P₀₁ + P₀₂ + P = 0,05 + 0,0625 + 5,0625 = 5,175 kW ;

P₁ + P₂ = 2,3 + 2,875 = 5,175 kW.

Astfel:

P₀₁ + P₀₂ + P = P₁ + P₂

Ceea ce era de asteptat, in cazul in care calculele au fost corect efectuate.

5 METODA GENRATORULUI ECHIVALENT DE TENSIUNE. REGIMUL CU SARCINA VARIABILA.

Enuntul problemei.

Fie circuitul din fig. 3-7 cu t.e.m. E₁ = 232 V si E₂ = 22 V, avand rezistente interne egale r₁ = r₂ = 0,4 Ω. Rezistenta R a sarcinii generatorului variaza intre (0 1) Ω.

Sa se determine relatia dintre curentul, puterea sarcinii si randamentul generatorului in functie de rezistenta R.

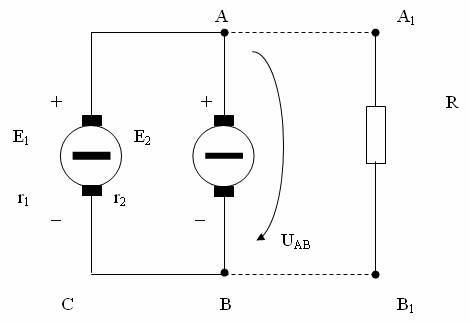
Fig. 3.8. Impartirea circuitului in parti interioare si exterioare.

Rezolvarea problemei.

1. Aplicarea metodei generatorului echivalent de tensiune. Aceasta metoda se recomanda pentru determinarea marimilor electrice (curenti tensiuni, puteri, etc.) pentru o latura a unui circuit complex. Avantajele metodei generatorului echivalent de tensiune, fata de celelalte metode, ies in evidenta atunci cand rezistenta laturii analizate este variabila (sarcina variabila), ca in problema de aici.

2. Stabilirea schemei echivalente. Circuitul examinat poate fi impartit fata de cele doua noduri, A si B, in doua parti (Fig. 3.8): ramura de studiat cu rezistenta R pe care o denumim sectorul exterior al schemei si restul circuitului care a mai ramas, denumit sectorul interior al schemei.

Cele doua parti, interna si externa, ale schemei din fig. 3.8 sunt conectate intre ele prin liniile punctate AA₁ si BB₁, fiecare linie apartinand unui nod.

Dupa teorema lui Thvenin tot sectorul interior al schemei poate fi inlocuit printr-o singura sursa de alimentare cu t.e.m. E_e si rezistenta R_e (fig. 3.9, latura ACB).

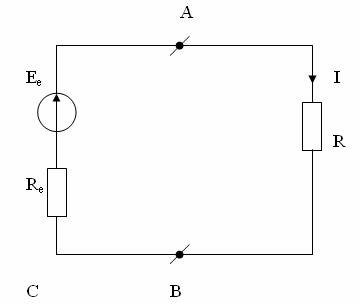
Fig. 3.9. Transformarea circuitului intr-o sursa echivalenta de tensiune.

Dupa o asemenea substitutie in circuitul din fig. 3.7 este transfigurat intr-un circuit simplu, neramificat, ca in fig. 3.9, a carui calcul nu prezinta dificultati.

Astfel, rezolvarea problemei trebuie sa inceapa prin determinarea parametrilor echivalenti, E_e si R_e, ai sectorului interior al schemei.

3. Calculul parametrilor sursei echivalente de tensiune. Dupa teorema lui Thvenin t.e.m. a sursei echivalente de tensiune E_e este egala cu tensiunea la bornele sectorului interior al circuitului atunci cand sectorul exterior este deconectat (regim de functionare in gol), tensiune notata cu U_ABO. In cazul nostru aceasta inseamna ca t.e.m. echivalenta E_e este egala cu tensiunea intre punctele A si B a schemei din fig. 3.8 pentru regimul de mers in gol E_e = U_ABO = E₁ - r₁ · I', I' fiind curentul prin conturul ABCA din fig. 3-8. Se observa ca, atunci cand rezistorul R este deconectat (eliminat din circuit), curentul I' se determina ca in paragraful 1-2:

E₁ - E₂ 232 - 228 4

I' = ───── = ─────── = ─── = 5 A .

r₁ + r₂ 0,8 0,8

Astfel incat rezulta:

E_e = E₁ - r₁ ∙ I' = 232 - 0,4 ∙ 5 = 230 V.

Aceasta tensiune E_e = U_ABO actioneaza in circuitul exterior din punctul A inspre punctul B, ca in fig. 3.9.

Se calculeaza, apoi, rezistenta interna a sursei echivalente R_e. Pentru aceasta se elimina toate t.e.m. din sectorul interior al schemei, (in cazul de aici E₁ si E₂) si se determina rezistenta echivalenta a schemei pentru regimul de mers in gol fata de bornele care delimiteaza partile circuitului, in cazul de aici A si B, din fig. 3.8.

r₁ ∙ r₂ r₁ r₂ 0,4

R_ABO = ────── = ─── = ──── = ──── = 0,2 Ω

r₁ + r₂ 2 2 2

Rezistenta echivalenta astfel obtinuta pentru sectorul interior al schemei reprezinta parametrul Re cautat al sursei echivalente de tensiune, adica R_e = R_ABO = 0,2 Ω

Determinarea relatiei intre curent si rezistenta I = f(R). Curentul in schema echivalenta, fig. 3.9 este:

E_e E_e 1 230 1 1,15 ∙ 10³

I = ───── = ─── ∙ ────── = ─── ∙ ────── = ──────

R_e + R R_e 1 + R/R_e 0,2 1 + R/R_e 1 + R/R_e