Calculul campului magnetic cvasistationar

Calculul campului magnetic cvasistationar

In medii liniare, omogene si izotrope, campul magnetic cvasistationar este descris de ecuatiile (5.6), (5.7) si (1.80):

,

,

,

iar potentialul magnetic satisface relatia (5.16):

.

5.3.1. Ecuatia lui Poisson pentru potentialul magnetic vector

Relatia (5.16), se mai poate scrie:

sau

.

Cu conditia de etalonare:

ecuatia (5.32) devine:

. (5.33)

Intr-un sistem cartezian, ecuatia vectoriala (5.33) se reduce la trei ecuatii scalare de tip Poisson:

(5.34)

Ecuatia de tip Poisson, care este o ecuatie cu derivate partiale de ordinul al doilea, se scrie sub una din formele:

,

adica:

,

sau

,

in care este o functie scalara iar o functie 'sursa' cunoscuta. Functia este diferita de zero intr-un domeniu . In afara domeniului, iar satisface ecuatia lui Laplace:

,

a carei solutie este de forma:

, (5.35)

unde se poate extinde, in principiu, asupra intregului spatiu (deoarece in afara lui avem ) iar este elementul de volum al domeniului .

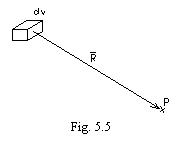Prin urmare, cu notatiile de la figura 5.5, solutiile sistemului (5.34) vor fi:

(5.36)

in care este volumul ocupat cu distributia densitatii de curent.

Rezulta potentialul magnetic vector:

(5.37)

si inductia magnetica:

. (5.38)

Deoarece nu este o functie de punctul P iar ^, rezulta :

(5.39)

si

.

5.3.2. Potentialul vector al circuitelor filiforme.

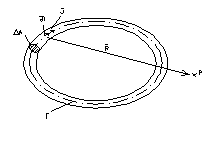
Potentialul vector al unui circuit electric filiform, (fig. 5.6), se va calcula cu relatia (5.37) in care iar si deoarece , rezulta:

iar expresia potentialului vector devine:

^.

In cazul a circuite filiforme parcurse de curentii potentialul magnetic vector va fi:

^.

Teorema Biot - Savart - Laplace stabileste relatia dintre intensitatea locala a campului magnetic si curentul electric de conductie care produce campul.

Ecuatia (5.40) aplicata circuitului din figura 5.6 se transforma succesiv, asa cum se procedeaza mai jos, obtinandu-se:

sau

^,

cunoscuta sub numele de Teorema Biot - Savart - Laplace.

Integrarea are sens numai pe contururi inchise, liniile de camp ale densitatii curentului elec-tric de conductie fiind linii inchise. Vectorul se orienteaza de la elementul catre punctul P.

Daca circuitul si punctul P se afla in acelasi plan (fig. 5.7), atunci , iar expresia intensitatii campului in P devine:

.

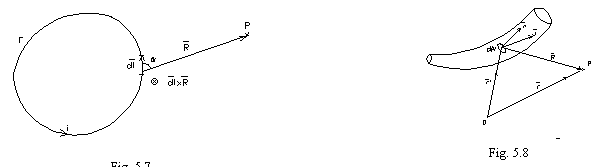
Pentru curenti in conductoare masive (fig. 5.8), se poate considera ca intensitatea elementara a campului magnetic in punctul este datorata tubului elementar de curent . Expresia acesteia, potrivit ecuatiei (5.43) va fi:

Deoarece si , se va scrie :

Integrandu-se in raport cu intreg volumul al conductorului se obtine expresia intensitatii campului produs in exterior de conductoarele masive aflate in regim electrocinetic:

. (5.45)

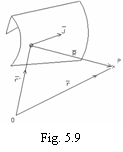
In cazul unei panze de curent de densitate - (fig. 5.9), se obtine in mod similar expresia:

. (5.46)