Campul magnetic in vid. Ecuatiile campului magnetic in vid

Campul magnetic in vid. Ecuatiile campului magnetic in vid

Campul magnetic in vid produs de curentii de conductie este descris in regim stationar si cvasistationar de ecuatiile rezultate din legea fluxului magnetic si legea circuitului magnetic. Pentru inductia magnetica si intensitatea campului magnetic aceste ecuatii sunt:

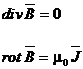(2.131)

respectiv:

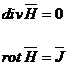(2.132)

Vom considera ca domeniul parcurs de curentii de conductie este finit si ca la infinit campul magnetic este nul. Asa cum am vazut campul inductiei magnetice fiind solenoidal inductia magnetica se poate exprima cu ajutorul potentialului magnetic vector (rel. 2.43):

A doua ecuatie din (2.131) devine:

(2.133)

Dar cum si alegand relatia (2.133) se poate scrie:

(2.134)

unde este operatorul lui Laplace aplicat marimii vectoriale .

In coordonate carteziene ecuatia (2.134) este echivalenta cu trei ecuatii cu derivate partiale scalare:

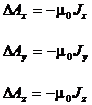
sau altfel scris:

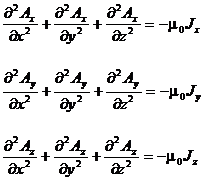(2.135)

Prin analogie cu solutia stabilita pentru potentialul electric scalar:

pentru oricare din componentele potentialului magnetic vector se poate scrie:

(2.136)

integrarea efectuandu-se pe volumul v al domeniului strabatut de curentii de conductie (fig. 2.39,a). In acest fel pentru potentialul magnetic vector solutia o putem pune sub forma:

(2.137)

sau:

(2.138)

Pentru cazul campului magnetic produs de conductoare filiforme, unde vectorii sunt colineari, iar vectorul de pozitie al elementelor de arie din sectiunea conductoarelor este practic constant, potentialul magnetic vector se poate scrie:

(2.139)

Integrala de linie (2.139) se efectueaza pe conturul G al conductoarelor parcurse de curentul i (fig. 2.39,b).

Inductia magnetica produsa intr-un punct P de o distributie de curenti de densitate va fi:

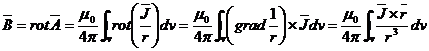(2.140)

La deducerea relatiei (2.140) s-a tinut seama de relatia matematica:

de faptul ca si de expresia lui 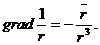Este necesar sa mentionam faptul ca expresia gradientului lui 1/r luata in considerare este valabila daca vectorul de pozitie r este orientat dinspre sursa de camp spre punctul P in care se calculeaza campul magnetic (fig. 2.39). In cazul in care se ia pentru calcule vectorul orientat dinspre punctul P spre sursa de camp magnetic, formula (2.140) se scrie:

(2.141)

Pentru conductoare filiforme tinand seama de expresia (2.139) a potentialului magnetic vector, inductia magnetica in vid intr-un punct este data de formula:

(2.142)

iar intensitatea campului magnetic este:

(2.143)

Formula (2.143) a intensitatii campului magnetic produs de conductoare filiforme parcurse de curenti este cunoscuta in literatura sub denumirea de formula Biot-Savart-Laplace. Aceasta formula se poate deduce pornind de la unele rezultate experimentale. Referitor la formula (2.143) se intalneste in literatura intensitatea de camp magnetic elementara care corespunde contributiei unui element de curent parcurs de curentul i la producerea campului magnetic intr-un punct P:

(2.144)

Daca inductia magnetica se calculeaza pe baza relatiei la

efectuarea calculelor se va alege sistemul de axe de coordonate cel mai convenabil. In sistemul de axe cartezian expresia inductiei magnetice va fi:

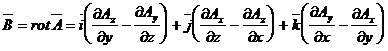(2.145)

Daca potentialul magnetic vector satisface conditia atunci scriind ecuatiile:

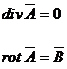(2.149)

este posibila stabilirea unei analogii fenomenologice pe baza ecuatiilor (2.149) si (2.131). Data fiind asemanarea intre ecuatiile lui si sa ne inchipuim ca dupa liniile inductiei magnetice ar exista o distributie de curenti de densitate proportionala cu valoarea inductiei magnetice. In acest caz campul magnetic al acestor curenti fictivi ar corespunde cu campul magnetic al potentialului magnetic vector .

Aceasta analogie ne da posibilitatea sa avem o imagine calitativa asupra liniilor de camp ale vectorului . In cazul unui conductor rectiliniu, de lungime foarte mare si de sectiune constanta in care densitatea de curent este paralela cu axa conductorului liniile de camp ale vectorului sunt drepte paralele cu conductorul. Pentru o spira parcursa de curent liniile de camp ale potentialului magnetic vector sunt cercuri cu centrul pe axa spirei situate in plane perpendiculare pe axa spirei.