BAZELE FIZICE ALE CAPACITATII DE RUPERE A MATERIALULUI

1 Elemente de cristalografie

Majoritatea corpurilor solide cristaline sunt formate din cristale ce reprezinta grupari de atomi ordonati in retele regulate tridimensionale. Nodurile unei retele sunt identice pentru orice grupare vecina acesteia.

Daca se considera un nod al unei grupari de atomi ca origine, oricare alt nod al gruparii acesteia se obtine cu relatia (1):

in care : (1)

reprezinta vectorul de pozitie al nodului considerat;

sunt vectorii fundamentali de translatie dupa directiile x, y, z;

u, v, w sunt numere intregi reprezentand coordonatele nodului considerat.

Fig. 1

Reteaua spatiala tridimensionala este definita de celula elementara sau celula unitate care stabileste lungimea vectorilor precum si unghiurile a b g, dintre acesti vectori, figura 1. Cele sase marimi respectiv a b g reprezinta parametrii retelei.

In functie de acesti parametrii pot fi definite 7 tipuri de sisteme cristaline sI 14 retele Barvais sau grupuri de translatie :

a) cubic: a = b = c, a b g

v     simpla;

v     cu volum centrat;

v     cu fete centrate.

b) tetragonal: a b ¹ c; a = b = 90 :

v     simpla;

v     cu volum centrat.

c) ortorombic: a ¹ b ¹ c; a b g

v     simpla;

v     cu volum centrat;

v     cu baze centrate;

v     cu fete centrate.

d) romboedral (trigonal): a = b = c, a b g < 120 ¹

e) hexagonal: a b ¹ c; a b 90 g

v     simpla.

f) monoclinic: a ¹ b ¹ c, a = g = 90 ¹ b:

v     simpla;

v     cu baze centrate.

g) triclinic: a ¹ b ¹ c, a ¹ b ¹ 90 :

v     simpla.

Numarul de noduri N ce revine unei celule elementare va fi:

unde: (2)

N_i - numarul de noduri interioare celulei;

N_f - numarul de noduri corespunzatoare unei fete;

N_c - numarul de noduri ce apartin colturilor celulei.

Celula hexagonala este tot un paralelipiped (nu este o prisma hexagonala), forma hexagonala provenind de la gruparea mai multor celule elementare.

Datorita unor factori externi ca: felul solicitarii, temperatura de lucru, precum sI in functie de forma retelei, cristalele se pot deforma prin unul din urmatoarele procese:

v       alunecare ;

v       maclare;

v       pierderea stabilitatii.

Deformarea prin alunecare

Se realizeaza prin alunecarea unei zone din cristal, una peste cealalta, de-a lungul unor plane cristalografice numite plane de alunecare ce coincid cu planele de densitate maxima. Combinatia dintre un plan de alunecare sI o directie de alunecare determina un sistem de alunecare. Alunecarea se produce atunci cand tensiunea tangentiala atinge o anumita valoare critica.

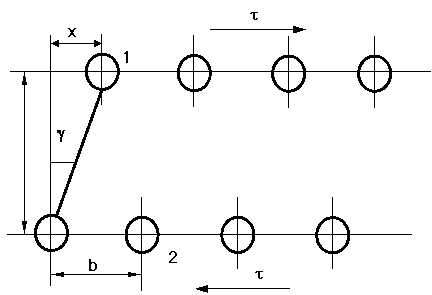Presupunand ca lunecarea se realizeaza prin miscarea de translatie a unui plan de atomi peste altul, fapt intalnit intr-o retea perfecta, se calculeaza tensiunea tangentiala teoretica t, care actioneaza intr-un plan de alunecare, in lungul unei directii de alunecare. Distanta dintre cei doi atomi in directia de alunecare este b, iar intre doua plane de alunecare alaturate este a. Tensiunea tangentiala t produce o deplasare x in directia de alunecare intre perechea de plane alaturate, figura 2.

Fig. 2

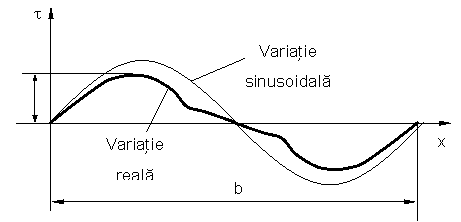
Se presupune ca tensiunea tangentiala are o variatie sinusoidala, figura 3 sI se determina cu relatia (3):

, unde (3)

b - perioada variatiei tensiunii;

t_max - amplitudinea solicitarii .

Lunecarea se produce printr-o miscare de translatie a unui plan de atomi peste altul, putandu-se sa se calculeze tensiunea tangentiala teoretica t care actioneaza in planul respectiv.

Conform legii lui Hooke : , unde    , figura 2.

Fig. 3

Pentru mici, , atunci:

sau , de unde:

(4)

Pentru    b = a rezulta ca:

(5)

Fenomenul de alunecare din cristale mai este pus in evidenta prin mecanismul de deplasare a dislocatiilor.

Dislocatia reprezinta un defect de retea cristalina bidimensional sau liniar care produce o deformare plastica a metalelor prin fenomenul de alunecare.

Alunecarea incepe atunci cand tensiunea tangentiala care actioneaza in planul de alunecare atinge o valoare critica numita tensiune tangentiala critica de alunecare.Aceasta valoare reprezinta echivalentul tensiunii de curgere dintr-un monocristal.

Se considera un monocristal cilindric cu aria sectiunii transversale A. Se noteaza cu x directia planului de alunecare, cuprinsa in planul cristalografic cu densitate mare, cu N normala la planul de alunecare, cu j unghiul dintre normala N sI directia de solicitare axiala data de sarcina P, respectiv cu yunghiul dintre directia de alunecare sI directia de solicitare , figura 4

Suprafata de monocristal cuprinsa in planul de alunecare va fi : iar componenta sarcinii P ce actioneaza in planul de alunecare este

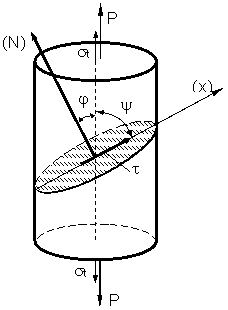Fig. 4

In aceste conditii, tensiunea tangentiala critica de alunecare, cuprinsa in acest plan va fi :

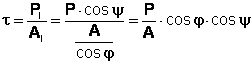
Dar reprezentand tensiunea normala produsa in monocristal de sarcina axiala P. Atunci tensiunea tangentiala critica de alunecare devine:

, (7)

relatie numita legea lui Schmid.

In cazul aliajelor, tensiunea t creste, ea depinzand de interactiunea dintre dislocatii, de actiunea dintre dislocatii sI celelalte defecte din retea: atomi interstitiali, vacante, atomi de substitutie. Aceasta este mai mare decat tensiunea tangentiala necesara deplasarii unei singure dislocatii, dar este mai mica decat cea necesara producerii alunecarii intr-o retea perfecta.

Deformarea prin maclare

Maclarea reprezinta un mod de deformare a cristalului care consta in deplasarea unei parti a retelei cristaline astfel incat aceasta se aseaza simetric fata de un plan, denumit plan de maclare. Fenomenul de maclare este favorizat de scaderea temperaturii sI de viteza de defornare.

Modul de deformare al unui cristal prin alunecare sau maclare la o anumita temperatura depinde de raportul dintre tensiunile tangentiale critice ale modurilor de deformare, deformarea producandu-se dupa modul caruia iI corespunde tensiunea tangentiala minima.

Deformabilitatea cea mai usoara prin maclare o au retelele cristaline de tipul hexagonal centrat datorita numarului redus de sisteme de alunecare.

Pierderea stabilitatii materialului apare la o solicitare de compresiune a cristalelor hexagonale, dupa o directie paralela cu planul de baza in urma caruia o anumita regiune a cristalului trece brusc intr-o pozitie inclinata. Aceasta comportare a cristalului este asemanatoare cu fenomenul de flambaj.

2 Moduri de rupere a retelelor cristaline

Metalele prezinta mai multe tipuri de rupere in functie de material, temperatura, starea de tensiune sI viteza de aplicare a sarcinii.

Din punct de vedere microstructural exista doua moduri fundamentale de rupere:

a)     rupere prin clivare (prin separare);

b)     rupere prin forfecare;

a)  Ruperea prin clivare se produce datorita componentei normale a tensiunii. Aceasta rupe legaturile atomice perpendiculare pe planele cristalografice cu legaturile cele mai slabe numite plane de separare sau clivare. Suprafata de rupere prin clivare are un aspect stralucitor sau grauntos datorita reflectarii luminii pe suprafata de clivaj.

b)       Ruperea prin forfecare este determinata de tensiunea tangentiala t care apare in planele de alunecare cu densitate maxima de atomi fiind o consecinta a ruperii legaturilor interatomice din aceste plane.

Suprafata de rupere prin forfecare are un aspect fibros de culoare gri, mata. Atunci cand cristalular un singur set de plane favorabil alunecarii, ruperea prin forfecare se produce dupa o sectiune inclinata, figura 5 a, respectiv cand exista doua astfel de plane sectiunea de rupere este dubla avand un caracter ascutit, figura 5 b.

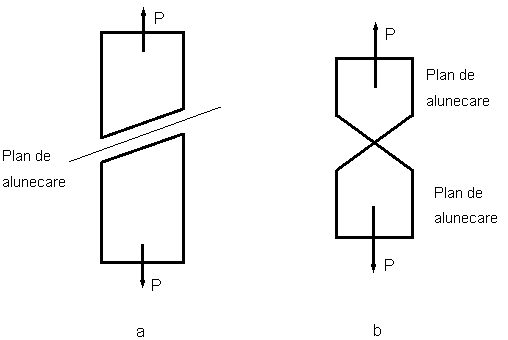La policristale pe langa ruperile prin clivare sI forfecare ce se produc transcristalin sau transgranular, fisura se propaga in interiorul cristalelor. Se mai produce sI o rupere intercristalina sau intergranulara, la care ruperea se propaga la limita de graunte.

Fig. 5

Din punct de vedere macroscopic ruperea materialelor poate fi:

a)     ductila;

b)     fragila;

a)    Ruperea ductila este insotita de deformatii mari, fiind necesare energii de rupere ridicate.

Policristalele din metale foarte ductile (aurul, aluminiul, plumbul), solicitate la tractiune, se pot gatui foarte mult, sectiunea transversala reducandu-se la un punct inaintea ruperii. La cele cu ductilitate medie, zona gatuita este redusa, ruperea incepand din centrul epruvetei sI se propaga catre exterior, producandu-se o rupere prin separare, prin forfecare, zona de rupere purtand numele de con-cupa, figura 6.

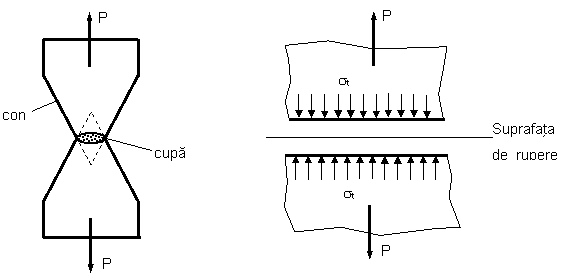
Fig.6 Fig. 7

b) Ruperea fragila este caracterizata de o suprafata de rupere perpendiculara pe tensiunea normala de intindere, figura 7. Deformatiile in acest caz sunt foarte mici sau lipsesc, iar energia de rupere este redusa. Limita dintre o rupere ductila sI una fragila este arbitrara, ea depinzand de modul de solicitare sI de punctul de vedere considerat.

3 Rezistenta de rupere teoretica

Rezistenta teoretica de rupere a metalelor este determinata de forta de interactiune dintre atomi, ca rezultat al compunerii fortei de atractie cu forta de respingere dintre acestia.

Fig. 8

Pentru echilibru, cand asupra cristalului nu actioneaza sarcini exterioare, distanta dintre atomi este r₀ . Daca insa un cristal este supus la intindere distanta r dintre atomi creste, forta de atractie crescand in valoare absoluta, atingand o valoare absoluta F_max , la care cristalul incepe sa cedeze.

Raportul dintre forta de interactiune sI suprafata pe care lucreaza aceasta se noteaza prin si se numeste forta de coeziune. Forta de coeziune maxima se noteaza cu s_t sI reprezinta rezistenta teoretica de rupere a cristalului. Curba de variatie a fortei de coeziune se apreciaza printr-o sinusoida de amplitudine s_t sI perioada l , reprezentand lungimea de unda a solicitarii. In acest caz forta de coeziune s se poate scrie :

, unde    (8)

u = r - r₀ , reprezinta deplasarea fata de pozitia de echilibru a celor doi atomi nesolicitati exterior. Rezistenta teoretica de rupere corespunde unei deplasari , figura 8. Lucrul mecanic efectuat in timpul ruperii, egal cu energia pe unitatea de suprafata acumulata de cristal , reprezinta aria portiunii cuprinsa intre o curba de variatie sinusoidala sI axa deplasarii r.

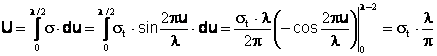, adica    (9)

(9)

Ruperea e pusa in evidenta de aparitia unei fisuri care prin propagare determina doua suprafete laterale ale sale. Daca se noteaza cu g energia specifica superficiala (pe unitatea de arie a fisurii) consumata pentru crearea acestei fisuri, energia totala specifica va fi:

, (sunt doua suprafete de rupere) (10)

Inlocuind, rezulta rezistenta teoretica de rupere:

, sau    (11)

(12)

Deoarece deplasarile u sunt foarte mici si , forta de coeziune se mai poate scrie:

(13)

Dar materialul respecta legea lui Hooke , s = E e si cum , atunci :

(14)

Din cele doua relatii rezulta:

(15)

Inlocuind in expresia rezistentei teoretice de rupere, se obtine:

, respectiv    (16)

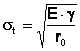(17)

Valorile pentru r₀, E, si g se determina teoretic in baza principiilor fizicii solidului sau experimental. Este folosita frecvent corelatia : care determina o valoare pentru s_t 0.22E. Utilizand alte aproximari, se obtine s_t E. Oricare din corelatiile folosite determina o rezistenta teoretica de rupere s_t mult mai mare decat rezistenta de rupere reala a monocristalelor, astfel : s_real s_t 0.02) E.

Cele doua rezistente de rupere sunt apropiate numai pentru metalele lipsite de dislocatii, pentru cristalele filiforme, denumite mustati.

4 Dislocatii sI deformatii ale structurilor cristaline

Defectele care apar in structurile cristaline pot fi:

- punctuale :

v     vacante;

v     atomi intercristalini;

v     atomi de impuritate substitutionala;

v     atomi de impuritate interstitiala.

- liniare:

v     dislocatii.

- de suprafata.

Dislocatia reprezinta un defect liniar care determina o deformare plastica la valori mai mici ale tensiunii s decat rezistenta teoretica de rupere s_t Acestea pot fi:

v     marginale , figura 9 a;

v     elicoidale, figura 9 b.

a.                                                                 b.

Fig. 9

Dislocatia se realizeaza datorita unei imperfectiuni ce poate fi un plan atomic suplimentar. Extremitatile acesteia determina linia de dislocatie. In cazul dislocatiei marginale directia de alunecare este perpendiculara pe linia de dislocatie, figura 9 a, iar in cazul dislocatiei elicoidale, figura 9 b, directia de alunecare este paralela cu linia de dislocatie. In acest caz nu mai este nevoie de un plan atomic suplimentar. Planul in care se face propagarea dislocatiei se numeste plan de alunecare.

Atunci cand un cristal este solicitat de o sarcina exterioara de intensitate ridicata, dislocatiile se deplaseaza producandu-se alunecari sI in consecinta o deformare a cristalului. Aceasta se realizeaza datorita unor forte care actioneaza in planul de alunecare sI sunt determinate de tensiunile tangentiale de alunecare t. Forta necesara pentru a pune in miscare o linie de dislocatie depinde atat de rezistenta de desfacere a legaturilor atomice ale retelei in planul de alunecare, cat sI de forta de frecare dintre linia de dislocatie sI defectele retelei respective, sau atomii interstitiali.

5 Ruperea brutala

In anumite situatii, in cristale sau policristale , unele fisuri, deja existente, cresc rapid trecand intr-o stare instabila, producandu-se astfel ruperea brutala. a) Criteriul energiei

In acest caz ruperea brusca se produce atunci cand lucrul mecanic al sarcinilor exterioare aplicate este mai mare decat energia de deformatie acumulata de corp sI energia elastica produsa la extensia fisurii.

Forta de extindere a fisurii    V reprezinta cantitatea de energie inmagazinata, eliberata de catre o epruveta fisurata, ca urmare a exinderii fisurii cu o suprafata egala cu unitatea.

Forta de extindere a fisurii V este o constanta de material care depinde de compozitia materialului, de microstructura, de temperatura, de viteza de solicitare, fiind o marime a tenacitatii materialului respectiv.

Daca se considera o placa de grosime mica, b = 1, de latime infinita care contine o fisura centrala eliptica, cu axele 2a, respectiv 2h, figura 10, energia eliberata la introducerea fisurii in placa va fi:

(18)

Variatia energiei elastice, in raport cu lungimea fisurii, la introducerea acesteia in masa de material este:

(19)

Fig. 10

iar aria A a fisurii variaza cu cantitatea dA. Cunoscand ca A 2a * 1 = 2a, rezulta ca dA = 2 * da, iar

Deci rezulta:

Marimea V a fortei de extensie a fisurii caracterizeaza rezistenta opusa la dezlipire de catre materialele adezive .

b) Ruperi fragile la deformatii constante

Fie o placa de grosime b, incastrata la ambele capete, aflata intr-o stare monoaxiala de tensiune, care contine o fisura laterala de lungime a. Fortele axiale nu efectueaza lucru mecanic deoarece incastrarile sunt fixe, figura 11 a, iar dL = 0. Din relatia bilantului energetic rezulta:

(21)

La propagarea fisurii, lungimea sa creste, materialul se relaxeaza iar energia de deformatie scade astfel ca variatia energiei dU este negativa.

Se aproximeaza fisura cu un semicilindru de raza a sI inaltime b, figura 11 b, iar energia eliberata la propagarea fisurii va fi:

, unde (22)

U_l este energia specifica de deformatie.

a.                                                 b.

Fig. 11

Variatia energiei eliberate devine:

(23)

Inlocuind rezulta forta critica de extindere a fisurii:

Folosind aceasta metoda se observa ca se obtine o valoare de doua ori mai mica decat prin metoda folosita anterior.

c) Ruperi fragile sub sarcini constante

Atunci cand capetele placii sunt libere, sarcinile aplicate efectueaza un lucru mecanic dL pozitiv, rezultand o energie de deformatie U pozitiva deci sI dU>0. Expresia marimii V_c este aceeasi si in aceasta situatie.

In concluzie :

v     ruperea brutala se produce la valori ale tensiunii mult mai mici decat s_e sau s_r

v     tensiunea de rupere este cu atat mai mica cu cat dimensiunea defectului (lungimea initiala a fisurii) este mai mare.