Calculul de verificare la vibratii torsionale

Calculul de verificare la vibratii torsionale

1. Determinarea sistemului oscilant echivalent

Studiul vibratiilor torsionale ale arborelui cotit consta in determinarea pulsatiilor si formelor oscilatiilor proprii ale arborelui (modurile de vibratie), determinarea amplitudinilor oscilatiilor fortate ale arborelui cotit si tensiunile corespunzatoare care se produc in acest arbore, in cazul diferitelor regimuri de exploatare.

Arborele cotit, fiind un sistem cu forma complicata, este inlocuit cu un arbore drept echivalent, a carui rigiditate trebuie sa fie identica cu rigiditatea arborelui cotit, iar momentele de inertie mecanica ale maselor legate de arborele cotit (inclusiv masa proprie) sunt identice pentru cei doi arbori, cotit real si drept echivalent. Cele doua conditii sunt determinate de natura fenomenului de oscilatie, care consta in transformarea periodica a energiei de deformare in energie cinetica si invers.

Arborele cotit, nefiind o grinda dreapta, nu permite determinarea cu exactitate a rigiditatii sale. Cele mai precise rezultate pentru determinarea rigiditatii arborelui cotit se obtin pe cale experimentala, prin masurarea unghiului de rasucire, cand arborele cotit este incarcat cu diferite momente:

, (1)

relatie cunoscuta din teoria elasticitatii, in care reprezinta unghiul cu care se rotesc, una fata de alta, doua sectiuni transversale ale arborelui, situate la distanta l [m], sub actiunea unui moment de torsiune [KNm]; G reprezinta modului de elasticitate transversal, iar momentul de inertie polar al acestuia. Rigiditatea arborelui (constanta elastica de rasucire) se defineste ca fiind:

(2)

Analog, pentru arborele echivalent imaginat ca un arbore drept, fara masa, de diametru , eventual gol la interior incarcat cu un numar de volanti (discuri), rigiditatea sa va fi:

(3)

Pentru simplificare, diametrul exterior si, eventual, interior al arborelui cotit se aleg egale cu diametrul exterior si, respectiv, interior ale fusului palier: si , astfel incat momentul de inertie polar al arborelui echivalent va fi egal cu cel al fusului palier, conform relatiei:

(4)

Punand conditia deja enuntata a identitatii rigiditatii celor doi arbori: , se poate deduce lungimea redusa a arborelui echivalent:

. (5)

Deformatia totala a elementelor de rigiditate diferita ale arborelui cotit sub actiunea unui moment de rasucire , va fi:

sau:

,

deci elasticitatea totala a arborelui (inversul rigiditatii) va fi:

(6)

unde cu n s-a notat numarul de elemente componente cu rigiditati diferite ale arborelui cotit si putand fi diferit de numarul i de coturi.

Pentru un cot, elasticitatea se determina tinand cont ca in componenta acestuia intra doua jumatati de fus palier (fiecare cu elasticitatea ), manetonul (avand elasticitatea ) si doua brate (cu elasticitatea ). Deci:

(7)

Cu relatia anterioara, lungimea redusa a cotului va fi:

(8)

Deoarece unele elemente au forme geometrice neregulate, lungimile reduse se determina pe cale experimentala. Relatiile de calcul pentru formele elastice cele mai uzitate sunt date in tabelul 1.

Astfel determinat, din punct de vedere al rigidita-

tii, arborele echivalent trebuie sa indeplineasca si conditia identitatii momentelor de inertie mecanice ale maselor in miscare de rotatie cu cele ale arborelui real.

Schematizarea consta in incarcarea arborelui cu

un numar de discuri (volanti), care corespund maselor aferente fiecarui cot al arborelui, ultimul disc fiind echivalent volantului (fig. 1).

In schema din figura 1 s-a notat cu , momentul de inertie mecanic al maselor in miscare aferente cotului de ordinul j, distanta redusa de la axa sa la cea a ultimului disc fiind . In figura 1,c s-a facut reducerea, in continuare, a sistemului echivalent cu sapte discuri din figura 1,b la un sistem mai simplu, cu trei discuri.

Momentele reduse, in acest ultim caz, ca si lungimile reduse fata de ultimul disc, sunt date in relatiile 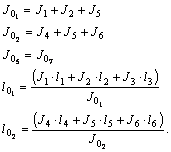(9).

(9)

Deci, va ramane de determinat, pentru precizarea completa a sistemului oscilant echivalent, momentul de inertie mecanic total al unui cot, J; pentru aceasta se aplica relatia:

(10)

In care este momentul de inertie propriu-zis al cotului, iar este momentul de inertie al maselor in miscare aferente cotului respectiv, redus la axa de rotatie. Prima marime se calculeaza din:

, (11)

unde este momentul de inertie mecanic al fusului palier (presupus, eventual, gaurit), dat de:

, (12)

Fig. 1

fiind lungimea fusului palier, iar densitatea materialului fusului.

Momentul de inertie mecanic al manetonului, , redus la axa de rotatie, este dat de:

(13)

iar este momentul de inertie al bratului, redus la axa de rotatie.

In cazul in care bratul are o forma complicata, se face divizarea acestuia intr-un numar de n portiuni, rezultate prin intersectia bratului cu n suprafete cilindrice coaxiale cu fusul palier, de raze R, ca in figura 2.

Cu notatiile de aici se poate deduce masa portiunii de ordinul j ca fiind:

, (14)

unde:

, (15)

iar momentul de inertie al elementului respectiv va fi:

, (16)

de unde:

. (17)

Ramane sa mai determinam momentul de inertie al maselor in miscare aferente cotului, redus la axa de rotatie, . Aceste mase sunt: masa bielei raportata la maneton, , ca si o fractiune x din masa a pieselor in miscare de translatie (a se vedea si 2.9).

Valoarea x se determina impunand conditia ca energia cinetica a maselor in miscare alternativa sa fie egala cu energia cinetica a unei mase echivalente aflata in miscare de rotatie cu manetonul si avand viteza periferica a acestuia ; deci: