Cuplaje bicardanice excentrice

Cuplaje bicardanice excentrice

Cuplajele cu cruci cardanice excentrice (cu cruci cardanice avand brate neconcurente) permit, in comparatie cu cele centrice, unghiuri mai mari intre axele arborilor. Acest important avantaj, datorat excentricitatii (neconcurentei) bratelor crucilor, este insotit de un dezavantaj care, in anumite situatii, nu poate fi acceptat: cu cresterea excentricitatii (distantei intre axele) bratelor crucilor creste dezechilibrarea cuplajului. Intr‑adevar, in acest caz, in timpul functionarii cu arborii necoaxiali, axa longitudinala de simetrie a elementului intermediar descrie o suprafata cilindrica necirculara, iar distanta dintre axele cuplelor de rotatie ale furcilor intermediare variaza intre o valoare minima si o valoare maxima (deci exista deplasari in cupla de translatie). In fig. 2.1,a sunt reprezentate doua pozitii particulare semnificative ale cuplajului bicardanic excentric:

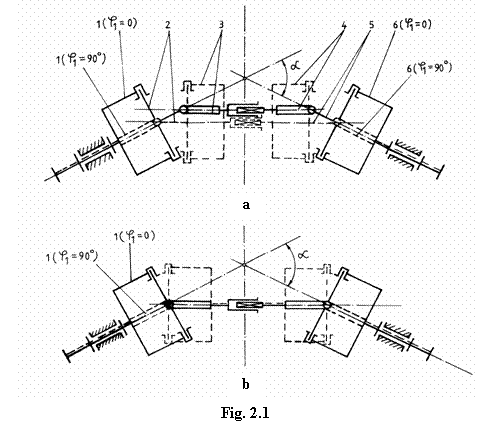
o pozitie reprezentata cu linie continua, in care distanta dintre axele cuplelor de rotatie ale furcilor intermediare este minima si o pozitie cu linie intrerupta, in care aceasta distanta devine maxima. Alaturat, in fig. 2.1,b, sunt reprezentate aceleasi pozitii in cazul particular al cuplajului bicardanic centric.

Spre deosebire de cuplajele excentrice, cuplajele cu cruci cardanice centrice (cruci cu brate concurente) sunt echilibrate si in cazul arborilor necoliniari, dar nu pot realiza unghiuri la fel de mari in comparatie cu primele (fig. 2.1,b).

Principalele dezavantaje ale ambelor tipuri de cuplaje sunt cauzate de cuple intermediare de translatie; aceste dezavantaje se refera la valorile ridicate ale solicitarilor si fortelor axiale de frecare din cupla intermediara de translatie si la cresterea gabaritului, cauzata de aceeasi cupla. Aceste cuplaje, in comparatie cu alte tipuri de cuplaje unghiulare, au constructii si tehnologii simple. Reducerea gabaritului se poate obtine prin eliminarea cuplei monomobile de translatie si transformarea cuplei de rotatie a unui arbore in cupla cilindrica, deci in cupla bimobila de rotatie si translatie, ca in varianta din fig. 2.2.

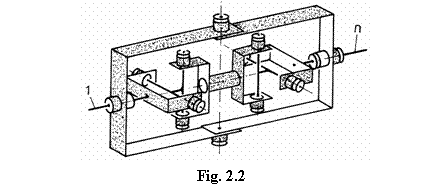
Aceasta noua varianta de cuplaj bicardanic are insa dezavantajul ca este cvasihomocinetica, deoarece nu se poate asigura decat aproximativ simetria fata de planul bisector al arborilor. In plus, in acest caz centrarea axiala directa se transforma in pseudocentrare axiala indirecta (fig. 2.2). Cvasihomocinetismul poate fi diminuat printr‑o corelare judicioasa a marimilor geometrice ale cuplajului. Asemenea cuplaje functioneaza optim in transmisii mecanice caracterizate prin puteri medii, turatii relativ mici si prin unghiuri mari intre axele arborilor. In premisa turatiilor mici, dezechilibrarea arborelui intermediar (v. fig. 2.2) devine neglijabila. Un exemplu tipic de utilizare a cuplajului bicardanic excentric este antrenarea rotilor motoare si directoare ale unor autocamioane grele.

In continuare este expusa o metoda de optimizare cinematica a mecanismului bimobil asociat cuplajului bicardanic excentric, in varianta structurala din fig. 2.2. Acest mecanism se obtine prin fixarea unui element al lantului cinematic de centrare (fig. 2.3,a) si are doi parametrii geometrici independenti: unghiul de rotatie al furcii de intrare 1 (j ) si unghiul dintre axele arborilor a (v. fig. 2.3).

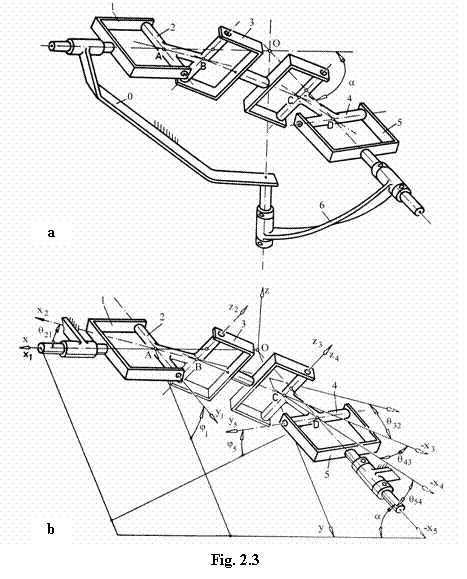
Obiectivul optimizarii cinematice, a mecanismului bicardanic excentric din fig. 2.3,a, este stabilirea unor corelatii intre marimile geometrice ale acestuia astfel incat, pentru un domeniu de variatie dat al unghiului a a a_max), heterocinetismul mecanismului sa fie minim. Analiza mecanismului bimobil din fig. 2.3,a poate fi redusa la analiza mecanismului monomobil din fig. 2.3,b, in care unghiul a se considera reglabil.

In modelarea geometrico-cinematica a mecanismului din fig. 2.3,b, vor fi utilizate urmatoarele notatii:

0, 1, 2,, 6 - numere de ordine ale elementelor cinematice componente.

Oxyz - triedru de referinta fix, in care planul Oxy coincide cu planul format de axele arborilor de intrare (1) si iesire (5)

Ax₁y₁z₁ (x₁ º x), Bx₂y₂z₂ (y₂ y₁), Cx₃y₃z₃ (z₃ z₂), Cx₄y₄z₄ (z₄ º z₃), Dx₅y₅z₅ (y₅ y₄) - triedre de referinta solidare cu elementele 1, 2, 3, 4 si 5 respectiv. 

a - unghiul dintre axele arborilor de intrare (1) si iesire (5);

j j - unghiurile de rotatie al arborilor de intrare (1) si iesire (5), fata de planul Oxy, format de axele acelorasi arbori;

y j j - abaterea de la homocinetism (folosita ca masura a heterocinetismului);

q q q q - unghiurile formate de perechile de axe (x₂, x₁); (x₃, x₂), (x₄,x₃) si respectiv (x₅, x₄); aceste unghiuri caracterizeaza deplasarile unghiulare relative ale elementelor din cuplele (2,1), (3,2), (4,3) si respectiv (5,4);

e = AB = CD - excentricitatea crucilor cardanice (distanta dintre axele bratelor unei cruci cardanice);

l = BC - lungimea arborelui intermediar (distanta dintre axele cuplelor de rotatie ale furcilor intermediare);

a = OA= lungimea variabila; b = OD = lungimea constanta;

A = a/l, B = b/l, u = a/b, E = e/l;

T_{i j} - matricea prin care se face trecerea de la triedru solidar cu elementul i la triedrul solidar cu elementul j;

l = (B + A cosa) / (A + B cosa) - factor de heterocinetism;

a - unghiul dintre arbori pentru care, in pozitia j = 45, abaterea de la homocinetism (y j j ) este nula;

D _{a = const)} = A_max - A_min    - alunecarea specifica maxima din cupla cilindrica, in timpul unei rotatii, in premiza ca unghiul dintre arbori este constant (a = const);

D _a = A_max(a) - A(a = 0) - alunecarea specifica maxima din cupla cilindrica, in premiza ca unghiul dintre arbori variaza de la valoarea zero la valoarea a, mecanismul ramanand in pozitia j

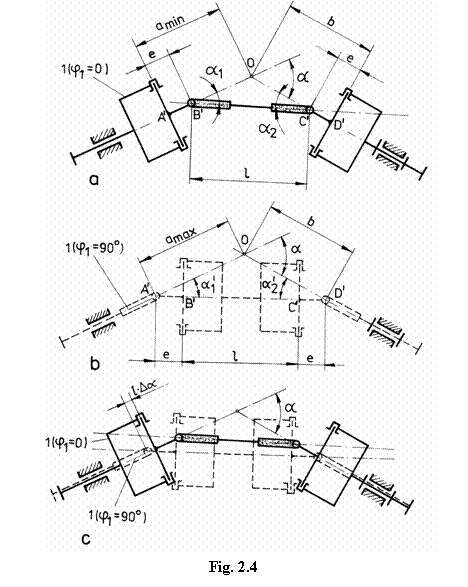
a a - unghiurile formate de axa arborelui intermediar cu axele arborilor de intrare (a ) si de iesire (a ) in pozitia j = 0 (fig. 2.4,a);

a a ' - unghiurile formate de axa arborelui intermediar cu axele arborilor de intrare (a ') si de iesire (a ') in pozitia j = 90 (fig. 2.4,b);

c = cos, s = sin - notatii prescurtate pentru functiile cosinus si respectiv sinus.

Pe baza fig. 2.3,b si a notatiilor de mai sus, se determina mai intai marimile variabile si necunoscute ale mecanismului in functie de marimile considerate cunoscute. Cu acest scop, se porneste de la urmatoarea observatie. Se considera un vector oarecare exprimat in triedrul bazei Oxyz; exprimand prin matricea de transformare, pe rand acest vector in triedrele solidare cu elementele si , se obtine din nou vectorul initial:

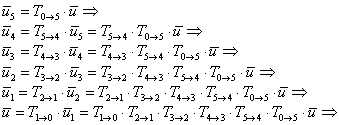(2.1)

Aceasta proprietate (2.1) se exprima analitic prin ecuatia matriceala (2.1,a):

(2.1,a)

in care I este notatia matricei unitate. Inmultind la stanga cu

ecuatia precedenta capata forma:

. (2.2)

		a
		b
	c

Rezolvarea acestei ecuatii permite determinarea marimilor geometrice dependente ale mecanismului (j , A = a/l, q q q q D_a D _a) in functie de marimile independente (j a) si de marimile constante (l,
B = b/l, E = e/l).

Conform fig. 2.3,b, matricele T_{i j} care intervin in ecuatia matriceala (2.2) au urmatoarele expresii:

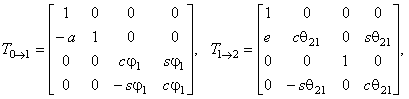(2.3), (2.4)

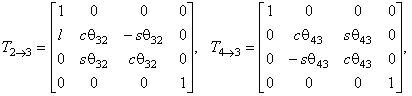(2.5), (2.6)

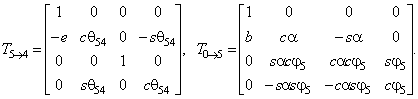(2.7), (2.8)

Prin efectuarea produselor matriceale din ecuatia (2.2), tinand seama de expresiile analitice ale matricelor (2.32.8), se obtine o ecuatie exprimata prin egalitatea a doua matrice. Facand egali termenii omologi din cele doua matrice, se obtine un sistem de 12 ecuatii scalare. Din acest sistem rezulta:

(2.9)

(2.9')

(2.9'')

(2.10)

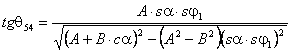, (2.11)

(2.12)

, (2.13)

. (2.13')

Aceste relatii nu sunt utilizabile, deoarece contin parametrul variabil A = A(j a, B, e) care este nedeterminat. Pentru fiecare stare geometrica a mecanismului, definita prin marimile (j a, B, e), parametrul A poate fi determinat cu ajutorul ecuatiei:

(2.14)

Deoarece nu poate fi rezolvata analitic, ecuatia F(A) = 0 se rezolva numeric, pe calculator. Pentru fiecare stare geometrica (j a, B, e) se obtine o solutie a parametrului A; cu valorile marimilor j a, B, e si A, se pot calcula marimile exprimate prin expresiile (2.9)(2.13).

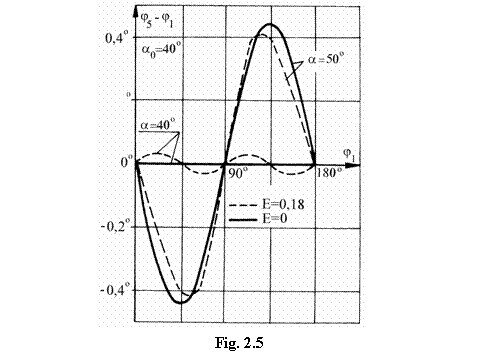
Din analiza abaterii de la homocinetism y j j , in functie de marimile j si a (fig. 2.5), se desprind doua proprietati ale mecanismului (fig. 2.3 si 2.5):

a) Pentru a = constant si pentru 0,98 £ l £ 1,02, abaterea de la homocinetism y j j este maxima pentru valoarea parametrului independent j 45. Aceasta afirmatie se justifica daca se observa ca pentru valorile 0,98 £ l £ 1,02 sunt acceptabile urmatoarele aproximari:

. (2.9'')

Ca urmare, in analiza comparativa a variantelor geometrice ale mecanismului, abaterea maxima de la homocinetism poate fi caracterizata, cu o precizie satisfacatoare, prin coeficientul l j

b) Fiecarei variante (B, e) ii corespunde un unghi a a pentru care, in pozitia j = 45, mecanismul este homocinetic (fig. 2.5): l a j = 45) =1. Unghiul a

a , denumit in continuare unghiul de homocinetism al starii (B, E, j ), ii corespunde egalitatea a = b <=> A = B.

In fig. 2.5 este reprezentata variatia abaterii de la homocinetism
y j j , pentru doua valori ale unghiului a a = 50 (E = 0; 0,18) si a a = 40 (E = 0; 0,18). In continuare, pe baza celor doua proprietati formulate (a si b), analiza cinematica a mecanismului se face in urmatoarele etape:

Se adopta valori pentru marimile a si E: a = 25, 35 si 45,
E = 0; 0,06; 0,12; 0,18.

Se determina parametrul B prin rezolvarea ecuatiei (2.14) scrisa sub forma:

(2.15)

Cu valoarea obtinuta pentru parametrul B, se calculeaza parametrul A pentru diverse valori ale unghiului a a = 0,, 50). Pentru fiecare set de valori (B, E, a), se determina parametrul A rezolvand numeric ecuatia:

(2.16)

Cu valoarea obtinuta pentru B si A, se calculeaza coeficientul de heterocinetism l(B, a, A(j

Se determina valorile extreme ale parametrului A: A_min = A(j = 0) si A_max = A(j = 90). Valorile A_min si A_max se obtin ca solutii ale ecuatiei:

(2.16')

in care, pentru j , se considera valorile 0 si respectiv 90. Expresiile acestor marimi se obtin mai simplu aplicand teorema sinusului in triunghiurile BOC (fig. 2.4,a) si AOD (fig. 2.4,b):

(2.17)

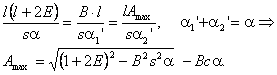(2.18)

Cu ajutorul formulelor (2.17) si (2.18) se calculeaza alunecarile specifice axiale ale arborelui

(2.19)

(2.20)

Rezultatele obtinute sunt sistematizate grafic in diagramele din fig. 2.6.

d

b

a

c

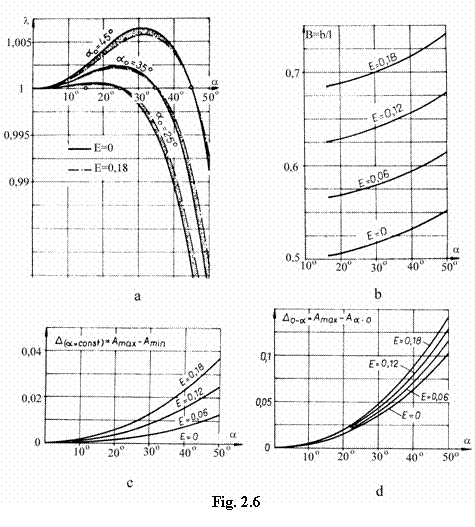
In fig. 2.6,a este ilustrata variatia coeficientului de heterocinetism
l j , in functie de unghiul dintre arbori a, pentru trei situatii semnificative: (a = 25, e = 0 0,18), (a = 35, e = 0 0,18) si (a = 45,
e = 0 0,18). Din analiza fig. 2.6,a rezulta ca in domeniul a a_max a_max £ 50), heterocinetismul mecanismului este influentat hotarator de alegerea unghiului de homocinetism a . Conform cu fig. 2.6,a, minimizarea heterocinetismului in domeniul a a_max se obtine alegand unghiul a astfel incat

. (2.21)

Egalitatea din aceasta relatie este recomandata in cazurile in care mecanismul functioneaza frecvent la unghiul a_max. In celelalte cazuri, se recomanda folosirea relatiei ca inegalitate. Corelatiile (2.21) sunt de regula satisfacute pentru unghiuri a a_max - (510); valorile mai mici ale unghiului a corespund inegalitatii din relatiile (2.21). Analiza figurilor 2.6,a si 2.5 evidentiaza, de asemenea, ca pentru un unghi a dat, excentricitatea (E) are o influenta nesemnificativa asupra heterocinetismului. Ca urmare, cresterea excentricitatii intre bratele crucilor cardanice nu are ca urmare cresterea heterocinetismului, ci cresterea unghiului maxim dintre arbori (a_max

Pentru patru valori ale parametrului E - fig. 2.3,b), in fig. 2.6,b am reprezentat variatia marimii in functie de unghiul de homocinetism a . In conformitate cu fig. 2.6,b, parametrul B creste cu cresterea unghiului a si cu cresterea excentricitatii dintre bratele furcilor (E). Graficele din fig. 2.6,b permit sinteza geometrica optima a mecanismului din fig. 2.3. Principalele etape ale acestei sinteze sunt urmatoarele trei:

Pe baza conditiilor concrete de functionare se stabilesc: unghiul maxim dintre arbori a_max), frecventa de functionare a mecanismului la acest unghi si excentricitatea specifica minima (E = e/l), care asigura realizarea unghiului a_max. Trebuie aleasa valoarea minima a parametrului E, deoarece cresterea acestuia accentueaza dezechilibrarea arborelui intermediar. Pentru a evidentia acest fapt, in fig. 2.4,c sunt reprezentate comparativ pozitiile j = 0 (v. fig. 2.4,a) si j = 90 (v. fig. 2.4,b) ale mecanismului bicardanic excentric (fig. 2.3). Din fig. 2.4,c rezulta ca axa arborelui intermediar descrie o suprafata necirculara, usor conica, al carei sectiune transversala creste in diametru cu cresterea excentricitatii dintre bratele crucilor cardanice.

Se determina unghiul de homocinetism optim cu ajutorul corelatiei (v. fig. 2.6,a): a a_max

Cunoscand marimile a si E, din fig. 2.6,b sau prin rezolvarea numerica a ecuatiei (2.15), se stabileste valoarea parametrului B = b/l.

Pentru patru valori ale parametrului E, in fig. 2.6,c si d sunt reprezentate variatiile alunecarilor specifice maxime ale arborelui 1 (fig. 2.3), in functie de unghiul dintre arbori a

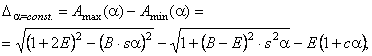(2.22)

(2.23)

Graficele din fig. 2.6,c si d evidentiaza cresterea alunecarilor specifice cu cresterea unghiului a si a parametrului E. Cunoscand unghiul a a_max si parametrul E, graficele din fig. 2.6,c permit determinarea alunecarii specifice maxime in timpul unei rotatii complete a arborelui 1 (fig. 2.3), in premiza ca unghiul dintre arbori este maxim si constant.

Folosind aceleasi date (a_max, E), graficele din fig. 2.6,d permit determinarea alunecarii specifice maxime a arborelui 1 (fig. 2.3) in premiza ca j = 90 (v. fig. 2.4,b) si ca unghiul dintre arbori variaza de la zero la a_max a a_max

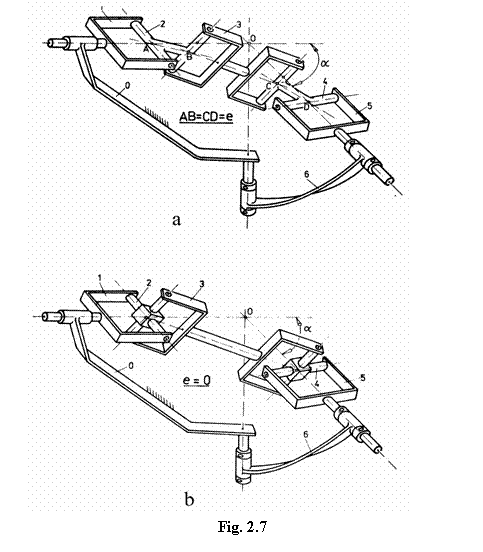
In concluzie, cresterea excentricitatii in mecanismele bicardanice permite marirea unghiului maxim intre arbori, ceea ce constituie un avantaj, dar cauzeaza, implicit, dezechilibrarea si aparitia alunecarii axiale, care sunt dezavantaje. Ca urmare, utilizarea cuplajului bicardanic, in care crucile au bratele neconcurente (v. fig. 2.7,a), este rationala numai in cazurile in care unghiul maxim dintre arbori (a_max) nu poate fi realizat prin utilizarea cuplajului bicardanic clasic (fig. 2.7,b).

In astfel de cazuri, valoarea maxima a excentricitatii admisibile este conditionata de realizarea unghiului a_max impus.

Sinteza geometrica a mecanismului bicardanic excentric poate fi descrisa succint prin urmatoarea succesiune de stabilire a marimilor caracteristice:
a_max (E, a B (A, q q q q D _a

a

b