Interactiunea rotilor cu calea de rulare nedeformabila

Interactiunea rotilor cu calea de rulare nedeformabila

Cinematica rotilor autovehiculelor

Pentru simplificare, in studiul cinematicii rotilor de autovehicul, in scopul explicarii calitative a fenomenelor, se considera atat roata cat si suprafata pe care se rostogoleste aceasta sunt absolut rigide. In aceasta situatie, contactul dintre roata si drum se face dupa o dreapta a carei proiectie, in figura 5.18 este data de punctul O₁, care reprezinta si axa instantanee de rotatie, I, in cazul rularii fara alunecare sau patinare. In realitate, deformatia rotii si solului este inevitabila si contactul intre roata si drum se face pe o suprafata, numita suprafata de sprijin a rotii. Functie de conditiile concrete de rostogolire a rotii, axa instantanee de rotatie poate ocupa diferite pozitii.

In cazul in care axa instantanee de rotatie I se afla pe suprafata de contact a rotii cu solul si coincide cu punctul O₁ (fig.5.18,a), atunci dreapta de sprijin pe sol ramane imobila si ca urmare se produce rostogolirea ideala, fara alunecarea sau patinarea rotii.

Daca axa instantanee de rotatie I este plasata deasupra punctului de tangenta O₁, zona de sprijin se deplaseaza in sens invers deplasarii autovehiculului, cu viteza v_d (fig.5.18,b). In acest caz roata se rostogoleste cu patinare, iar viteza reala v_a de deplasare a autovehiculului este mai mica decat viteza teoretica v_t.

Daca axa instantanee de rotatie I este plasata sub zona de contact a rotii cu calea de rulare (fig.5.18,c), iar zona de sprijin se deplaseaza in sensul deplasarii autovehiculului cu viteza v_d, roata se rostogoleste cu alunecare, iar viteza reala v_a de deplasare a autovehiculului este mai mare decat cea teoretica v_t.

Daca roata din figura 5.18,c este franata brusc, pana la blocare, centrul instantaneu de rotatie, I, se deplaseaza la infinit (fig.5.18,d), iar miscarea devine o miscare de translatie in sensul deplasarii autovehiculului cu viteza v_d=v_a.

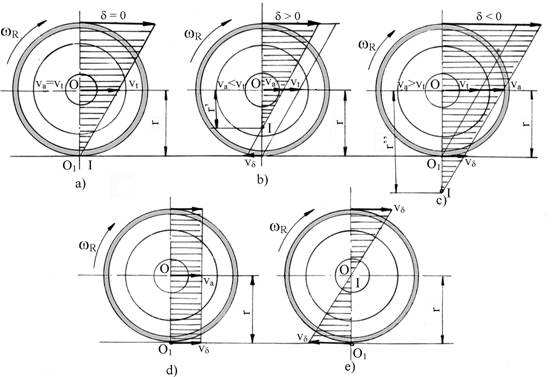
Fig.5.18. Cinematica rotii de autovehicul.

In cazul in care aderenta rotii cu solul este foarte mica (cale de rulare acoperita cu gheata sau zapada), roata poate patina cu viteza v_d, fara ca autovehiculul sa se deplaseze v_a=0, iar miscarea devine o miscare de rotatie cu axa fixa (fig.5.18,e).

In figura 5.18, cu d s-a notat coeficientul patinarii sau al alunecarii.

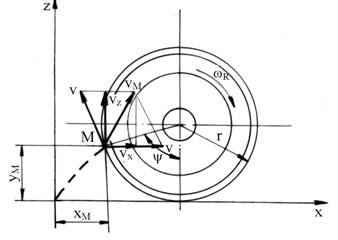In figura 5.19 este prezentata schematic o roata de raza r, care se rostogoleste fara patinare sau alunecare cu viteza unghiulara w_R pe un drum nedeformabil. Pe circumferinta rotii se considera un punct M, care se rostogoleste cu un unghi y. La un anumit moment, punctul considerat are o viteza de rotatie v=rw_R in jurul centrului rotii si o viteza de translatie de aceiasi valoare v. Prin compunerea celor doua viteze se obtine o viteza rezultanta v_M ale carei componente v_x si v_z se pot determina grafic sau analitic. Marimea vitezei v_M si a componentelor sale v_x si v_z depinde de pozitia punctului considerat.

Fig.5.19. Vitezele si deplasarile unui punct

oarecare al rotii la rostogolirea acestuia.

Prin rostogolirea rotii, traiectoria punctului M este o cicloida, care are ecuatiile parametrice:

(5.15)

Daca se scrie unghiul de rotatie al rotii y functie de viteza unghiulara w_R a rotii si timpul t (y w_R t), se obtine:

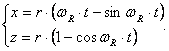(5.16)

Traiectoria completa a punctului M pentru o rotatie a rotii (y p) este prezentata in figura 5.20.

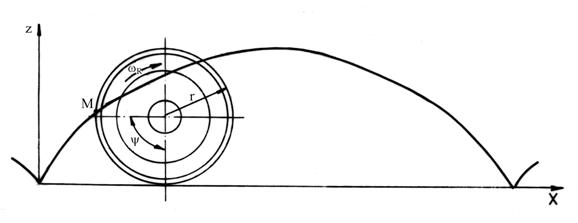
Fig.5.20. Traiectoria completa a unui punct oarecare al rotii la o rotatie completa a acesteia.

Prin derivarea ecuatiilor 5.16 in raport cu timpul, pentru o viteza unghiulara a rotii w_R constanta se obtin componentele vitezei dupa cele doua axe v_x si v_y:

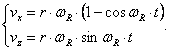(5.17)

Daca tinem seama ca v_t=r w_R ,unde v_t este viteza teoretica de translatie, din relatia 5.17 rezulta:

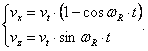(5.18)

Vitezele v_x si v_y variaza functie de unghiul y intre limitele:

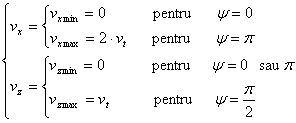(5.19)

Fata de suprafata drumului miscarea rotii este o miscare plan paralela si ca urmare miscarea punctului M are doua componente:

o translatie cu viteza v, dupa traiectorii paralele;

o rotatie cu aceiasi viteza v.

Prin insumarea vectoriala a celor doua componente se obtine viteza rezultanta v_M, care are urmatoarea expresie:

(5.20)

Componentele acceleratiei punctului M a_x si a_z, sunt date de relatiile:

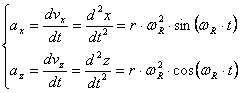(5.21)

Prin compunerea celor doua componente ale acceleratiei se determina acceleratia punctului M, cu relatia:

(5.22)

Din relatia 5.22 rezulta ca acceleratia punctului M este constanta, este orientata dupa raza cercului, respectiv este centripeta.

In cazul rostogolirii cu patinare (fig. 5.18,b), raza cercului de rostogolire se micsoreaza de la r=OO₁ la r'=OI, r'<r. Curba descrisa de punctul M in acest caz este o trohoida scurtata, iar ecuatiile ei parametrice sunt:

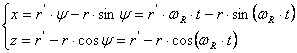. (5.23)

Prin derivarea ecuatiilor 5.23 in raport cu timpul se obtin componentele vitezei:

(5.24)

Se constata ca in pozitia superioara a punctului M, unde viteza unui punct de pe coama pneului avea in primul caz viteza maxima (v_xmax=2v_a), egala cu dublul vitezei autovehiculului, acum viteza in aceiasi pozitie va fi:

, (5.25)

iar viteza minima va fi:

(5.26)

Datorita acestui fapt, viteza punctului O₁ (v_d) fiind de sens contrar directiei de inaintare a autovehiculului, va avea loc o patinare a rotii, viteza de inaintare a autovehiculului fiind data de relatia:

(5.27)

Fenomenul de rostogolire cu patinare se intalneste la rotile motoare ale autovehiculelor, fiind caracterizat de coeficientul patinarii care se calculeaza cu relatia:

(5.28)

unde: l este drumul parcurs; n numarul de rotatii efectuat de roata pe distanta l; r raza dinamica a rotii.

In cazul rostogolirii cu alunecare (fig. 5.18,c) raza cercului de rostogolire se mareste la r''=OI, unde r''>r. Curba descrisa de punctul M in acest caz este o trohoida alungita, iar ecuatiile ei parametrice sunt:

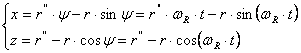(5.30)

Prin derivarea ecuatiilor 5.30 in raport cu timpul se obtin componentele vitezei:

(5.31)

Viteza maxima in acest caz este:

, (5.32)

iar viteza minima va fi:

(5.33)

Fenomenul de rostogolire cu alunecare se intalneste la rotile franate ale autovehiculelor, fiind caracterizat de coeficientul alunecarii care se calculeaza cu relatia:

(5.34)

unde: l este drumul parcurs; n numarul de rotatii efectuat de roata pe distanta l; r raza dinamica a rotii.

Dinamica rotilor de autovehicul

In timpul deplasarii autovehiculului, rotile acestuia ruleaza pe suprafata drumului datorita uneia dintre urmatoarele actiuni:

o forta de impingere sau tragere F aplicata in centrul rotii, cazul rotii conduse figura 5.21,a;

un moment activ M_R, cazul rotii motoare figura 5.21,b;

un moment de franare M_f, cazul rotii franate figura 5.21,c.

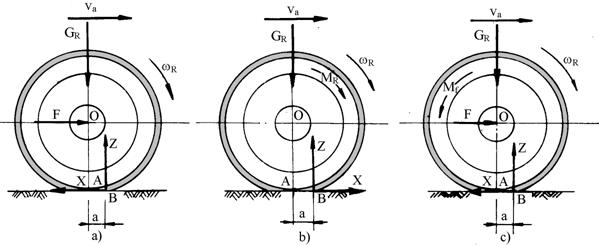
Fig.5.21. Fortele si momentele care actioneaza asupra rotilor de autovehicul.

In functie de fortele si momentele care actioneaza asupra rotilor de autovehicule acestea pot fi: roti motoare sau antrenate, cand asupra lor actioneaza un moment motor M_R, care are acelasi sens cu viteza unghiulara w_R; roti conduse sau neantrenate, cand asupra lor se aplica forte de impingere sau de tragere F, care au acelasi sens cu sensul de deplasare sau forte de retinere de sens opus sensului deplasarii; roti franate, cand asupra lor se aplica un moment de franare M_f, care are sens opus celui al vitezei unghiulare w_R

Ca urmare a actiunilor prezentate anterior, in zona de contact a rotii deformabile cu drumul nedeformabil ia nastere reactiunea tangentiale X si reactiunea normala Z, care sunt aplicate in punctul B, situat la distanta a fata de axa de simetrie a rotii OA. Deplasarea punctului de aplicare a reactiunilor se datoreaza faptului ca deformatia pneului este mai mare in partea din fata a suprafetei de contact decat in partea din spate. In cazul rotii franate si a rotii conduse, figura 5.21,a si c, reactiunea tangentiala X este indreptata in sens invers deplasarii, iar in cazul rotii motoare aceasta este indreptata in acelasi sens cu deplasarea autovehiculului, constituind o forta de impingere care se numeste forta de tractiune la roata.

Echilibrul rotii motoare

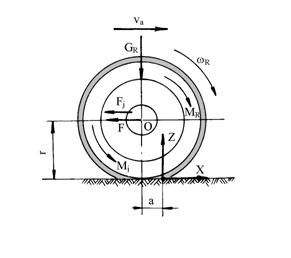Daca se neglijeaza rezistenta aerului, fortele, reactiunile si momentele care actioneaza la rularea unei roti motoare sunt aratate in figura 5.22.

Daca rostogolirea rotii are loc cu viteza constanta, ea se deplaseaza sub actiunea momentului la roata M_R, care da nastere la o reactiune tangentiala X, in zona de contact dintre roata si drum, indreptata in acelasi sens cu deplasarea autovehiculului. Aceasta reactiune tangentiala se opune patinarii rotii si constituie o forta de impingere sau forta de tractiune la roata, care la randul ei da nastere la o reactiune F, egala si de sens contrar cu X, aplicata la axul rotii.

Fig.5.22. Fortele, momentele si reactiunile

care actioneaza asupra rotii motoare.

Reactiunea normala Z este egala cu greutatea repartizata pe roata G_R si in raport cu centrul rotii da nastere la moment de rezistenta la rulare M_r:

(5.35)

Momentul la roata poate avea valori cuprinse intre o limita minima, sub care nu este posibila rularea rotii, si o limita maxima peste care incepe patinarea rotii. Limita minima este conditionata de egalitatea momentului M_R cu cea a momentului de rezistenta la rulare M_r. In acelasi timp limita maxima este conditionata de valoarea maxima a aderentei dintre roata si drum jZ. De aici, rezulta limitele posibile pentru reactiunea tangentiala la roata motoare, pentru ca aceasta sa ruleze fara patinare si anume:

(5.36)

Din conditiile de echilibru a rotii motoare pentru miscarea uniforma (v_a=constant), scriind ecuatiile de proiectii pe axele orizontala si verticala si ecuatia momentelor in raport cu centrul rotii, se obtine:

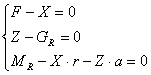(5.37)

Cunoscand ca M_R=F_R.r, se poate scrie:

(5.38)

sau daca avem in vedere ca reactiunea tangentiala X, reprezinta forta de tractiune F_t

(5.38')

de unde:

(5.39)

Se poate trage concluzia ca forta de tractiune F_t este egala cu diferenta dintre forta periferica la roata datorata momentului M_R si forta de rezistenta la rulare F_r.

Daca se introduce limita maxima a reactiunii tangentiale data de relatia 5.36 in ecuatia de echilibru 5.38, se obtine conditia rularii fara patinare pentru miscarea uniforma:

(5.40)

Valoarea maxima a fortei la roata F_R este limitata de conditia de aderenta, relatia 5.40, pentru valori mai mari roata motoare patineaza.

In cazul deplasarii accelerate ecuatiile de echilibru ale rotii motoare sunt:

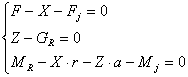, (5.41)

sau:

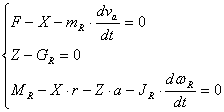(5.41')

unde: F_j este forta de inertie a rotii, care se opune mariri vitezei de translatie; M_j este momentul fortei de inertie, care se opune accelerarii rostogolirii rotii; m_R este masa rotii; J_R momentul de inertie al rotii in raport cu axa de rotatie; w_R este viteza unghiulara a rotii.

Cunoscand ca M_R=F_Rr, se obtine:

(5.42)

de unde:

(5.43)

sau:

(5.43')

Expresia fortei de tractiune F este:

. (5.44)

Daca se introduce limita maxima a reactiunii tangentiale data de relatia 5.36 in ecuatia de echilibru 5.43, se obtine conditia rularii fara patinare pentru miscarea accelerata:

(5.45)

Analizand relatia 5.45 se poate trage concluzia ca la deplasarea rotii motoare in regim variabil, forta de tractiune este diminuata fata de regimul uniform de miscare cu valoarea fortelor de inertie care apar la accelerare.

Echilibrul rotii conduse

Daca se neglijeaza rezistenta aerului, fortele, reactiunile si momentele care actioneaza la rularea unei roti conduse sunt aratate in figura 5.23. La rostogolirea rotii cu viteza constanta, deplasarea rotii are loc sub actiunea fortei F, aplicata la axul rotii, care determina aplicarea unei reactiuni tangentiale in zona de contact a rotii cu calea de rulare considerata nedeformabila. Aceasta reactiune, este indreptata impotriva sensului de deplasare a autovehiculului, si are valorile cuprinse intre:

(5.46)

unde: f este coeficientul de rezistenta la rulare; j este coeficientul de aderenta.

Din conditia de echilibru a rotii conduse, in cazul deplasarii acesteia cu viteza constanta se obtin urmatoarele ecuatii de echilibru:

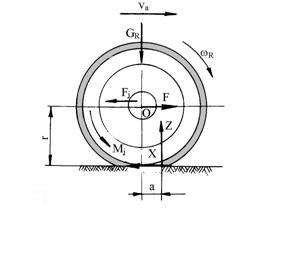
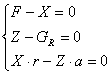
(5.47)

de unde:

(5.48)

Fig.5.23. Fortele si momentele care

actioneaza asupra rotii conduse.

Raportul a/r=f reprezinta coeficientul de rezistenta la rulare, care ia in considerare pierderile care au loc in timpul rularii rotii de autovehicul, iar forta de rezistenta la rulare pentru roata condusa este:

(5.49)

Daca in relatia 5.48 se introduce limita maxima a reactiunii tangentiale din 5.46, se obtine conditia rularii pentru roata condusa sub forma:

(5.50)

Daca coeficientul de aderenta are valori mai mici decat cele permise de conditia de rulare, 5.50, roata condusa nu mai ruleaza pe suprafata de rulare si incepe sa alunece in directia deplasarii autovehiculului.

In cazul deplasarii accelerate ecuatiile de echilibru ale rotii conduse sunt:

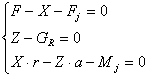, (5.51)

sau:

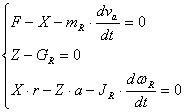(5.51')

unde: F_j este forta de inertie a rotii, care se opune mariri vitezei de translatie; M_j este momentul fortei de inertie, care se opune accelerarii rostogolirii rotii; m_R este masa rotii; J_R momentul de inertie al rotii in raport cu axa de rotatie; w_R este viteza unghiulara a rotii.

Din ecuatiile de echilibrul 5.51' rezulta:

(5.52)

sau:

(5.53)

Prin urmare, in cazul rularii rotii cu viteza variabila, forta de impingere sau tragere F trebuie sa invinga rezistentele la rulare a rotii si fortele de inertie ale acesteia, care apar in miscarea de rotatie si de translatie a rotii.

Echilibrul rotii franate

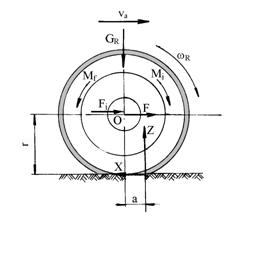
Daca se neglijeaza rezistenta aerului, fortele, reactiunile si momentele care actioneaza la rularea unei roti conduse sunt aratate in figura 5.24. Din figura se observa ca asupra rotii franate actioneaza un moment de franare M_f, care se opune rotiri. In axul rotii actioneaza o forta F, care are acelasi sens cu deplasarea autovehiculului si determina aparitia reactiunii tangentiale X din partea caii de rulare, care este indreptata in sens contrar sensului de deplasare al autovehiculului.

Fig.5.24. Fortele si momentele care

actioneaza asupra rotii franate.

Momentul de franare M_f poate avea valori cuprinse intre o limita minima egala cu zero, si o limita maxima peste care roata franata incepe alunecarea. Limita maxima este conditionata de valoarea maxima a aderentei dintre roata si drum jZ, iar cea minima este conditionata de rezistenta la rulare fZ. De aici, rezulta limitele posibile pentru reactiunea tangentiala la roata franata, pentru ca aceasta sa ruleze fara alunecare si anume:

(5.54)

unde: f este coeficientul de rezistenta la rulare; j este coeficientul de aderenta.

Din conditia de echilibru a rotii franate, in cazul deplasarii acesteia cu viteza constanta se obtin urmatoarele ecuatii de echilibru:

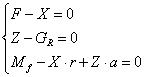(5.55)

Cunoscand ca M_f=F_fr, rezulta:

, (5.56)

sau:

, (5.57)

unde: F_f este forta de franare aplicata la roata, datorata momentului de franare M_f.

Din relatia 5.57, se obtine:

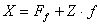(5.58)

Daca in relatia 5.58 se introduce limita maxima a reactiunii tangentiale din 5.54, se obtine conditia rularii fara alunecare pentru roata franata sub forma:

(5.59)

sau:

(5.59')

La valori ale fortei de franare F_f mai mari decat cele impuse prin conditia de rulare, relatia 5.59', rota franata inceteaza rostogolirea pe calea de rulare si incepe sa alunece in directia deplasarii autovehiculului.

In cazul deplasarii accelerate ecuatiile de echilibru ale rotii franate sunt:

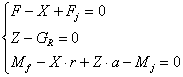(5.60)

sau:

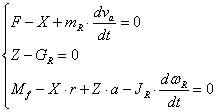(5.60')

unde: F_j este forta de inertie a rotii, care se opune micsorarii vitezei de translatie; M_j este momentul fortei de inertie, care se opune incetinirii rostogolirii rotii; m_R este masa rotii; J_R momentul de inertie al rotii in raport cu axa de rotatie; w_R este viteza unghiulara a rotii.

In acest caz expresia reactiunii tangentiale X este:

(5.61)

si a fortei de franare:

(5.62)

sau:

(5.62')

Rezulta ca in regim de franare decelerata forta de franare este diminuata de fortele de inertie ale rotii in miscare de rotatie si de translatie.

Limitarea de catre aderenta a momentelor si fortelor care incarca roata de autovehicul

Atat in cazul rotii motoare cat si in cazul rotii libere sau a rotii franate s-a notat cu X reactiunea tangentiala (longitudinala) a caii de rulare asupra rotii. Reactiunea X paralela cu calea de rulare se numeste forta de aderenta.

In cazul rularii pe drumuri cu suprafete tari, nedeformabile, forta de aderenta apare in principal datorita frecarii dintre pneu si calea de rulare, fiind similara unei forte de frecare. La rularea pe drumuri deformabile, forta de aderenta este conditionata si de rezistenta la rupere a materialului drumului si de adancimea de patrundere a pneului in straturile caii de rulare.

Marimea fortei de aderenta X depinde de valoarea reactiunii normale Z si de natura suprafetelor aflate in contact. In conditii precizate de incarcare Z, tip de anvelopa, presiune de umflare, stare de uzura a benzii de rulare pentru o categorie de drum caracterizat prin material si stare (umed, uscat, etc.) forta de aderenta nu poate sa depaseasca o valoare limita. Valoarea maxima a fortei de aderenta se numeste aderenta si se noteaza cu X_max.

Raportul dintre valoarea maxima a fortei de aderenta X_max pentru anumite conditii date si incarcarea normala pe roata Z se numeste coeficient de aderenta:

(5.63)

Din relatiile 5.37, care reprezinta ecuatiile de echilibru ale rotii motoare, se poate deduce relatia:

(5.64)

care exprima dependenta dintre forta de aderenta X si forta de rezistenta la rulare fZ. Datorita limitarii fortei de aderenta la valoarea X_max=jZ apare o limitare a momentului la roata M_R la o valoare maxima data de relatia:

(5.65)

Prin impartirea relatiei 5.65 cu raza dinamica r_d, se obtine valoarea maxima a fortei la roata limitata de aderenta:

(5.66)

Pentru intregul autovehicul aderenta se calculeaza cu relatia:

(5.67)

unde G_ad este greutatea aderenta si reprezinta partea din greutatea totala a autovehiculului G_a care revine rotilor motoare.

In cazul autovehiculelor cu tractiune integrala, la deplasarea pe drum orizontal aderenta se calculeaza cu relatia:

(5.68)

iar la deplasarea pe o panta cu unghiul de inclinare a aceasta se calculeaza cu relatia:

(5.68)

In mod corespunzator se modifica si momentul maxim la roata si forta maxima la roata:

(5.69)

In cazul lipsei fortei de aderenta, X=0, pentru invingerea momentului de rezistenta la rulare este necesar un moment minim la roata motoare:

(5.70)

Deci limitele intre care poate sa varieze momentul la roata M_R sunt:

(5.71)

Prin impartirea relatiei 5.71 cu produsul r_dZ se obtine:

, (5.72)

sau:

, (5.73)

unde s-a notat cu x_R=F_R/Z forta la roata specifica.

Deci, se poate afirma ca momentul motor aplicat rotii poate varia intre o valoare minima determinata din conditia de rulare si o valoare maxima la care incepe patinarea. Daca valoarea maxima M_Rmax, data de relatia 5.65 sau 5.71, este depasita atunci se produce patinarea sau alunecarea, care duce la aparitia unei viteze relative intre pneu si calea de rulare in zona de contact. Patinarea are o influenta deosebita asupra coeficientului de aderenta.

Din relatiile 5.55, care reprezinta ecuatiile de echilibru ale rotii franate, se poate deduce relatia:

(5.74)

Pentru X=X_max, se obtine expresia momentului maxim de franare:

(5.75)

pe care il poate prelua roata.

Limitele de variatie ale momentului de franare sunt:

(5.76)

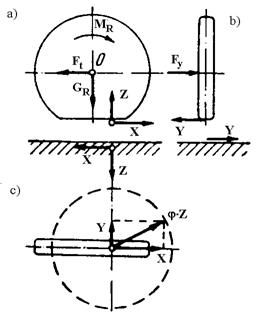Daca asupra rotii motoare incarcate cu un moment MR, care produce forta aderenta X actioneaza si o forta transversala Fy (fig.5.25), atunci reactiunea caii de rulare va avea si o componenta de aderenta transversala Y=Fy. Rezultanta fortelor de aderenta X si Y nu va putea depasi ca valoare forta de aderenta maxima permisa de calea de rulare si incarcarea pe roata Z:

Oricare ar fi raportul dintre marimile X si Z rezultanta lor va fi raza cercului a carui ecuatie este:

(5.78)

Se observa ca pe masura ce momentul la roata creste si deci forta de aderenta X va fi mai mare, componenta transversala disponibila a aderentei Y se va micsora. La limita cand X=X_max=jZ rezulta Y=0, adica roata nu poate sa preia forte laterale fara sa alunece lateral (derapeze).

Fig.5.25. Fortele de aderenta longitudinale

si transversale.

Componenta transversala Z a aderentei se numeste forta de ghidare laterala a rotii si mentine autovehiculul pe traiectoria comandata in viraj sau se opune deplasarii laterale cauzate de inclinarea drumului. Cercul de raza jZ se numeste cerc de aderenta si reprezinta limita ghidarii prin aderenta. Rezulta ca in cazul rotilor incarcate cu un moment motor sau un moment de franare, posibilitatile de ghidare ale autovehiculului scad. Acest lucru explica deraparea autovehiculului la franari sau accelerari puternice in curbe.

Trebuie subliniat faptul ca in cele prezentate anterior s-a admis ca forta de aderenta are aceiasi valoare pe orice directie in pata de contact. In realitate, datorita proprietatilor anizotropice ale anvelopei, aderenta difera de la o directie la alta. Ca urmare in locul cercului de aderenta trebuie avuta in vedere o elipsa de aderenta.

Studiul aderentei dintre pneu si calea de rulare

Asa cum s-a mai aratat reactiunea tangentiala maxima X_max, care poate lua nastere intre pneu si calea de rulare este data de relatia:

, (5.79)

unde j este coeficientul de aderenta si Z este ratiunea normala a caii de rulare asupra rotii.

Daca se depaseste aceasta valoare prin transmiterea unui moment la roata mai mare, apare alunecarea elementelor pneului pe calea de rulare. In acest caz reactiunea tangentiala va fi:

(5.80)

unde j_a este coeficientul de frecare la alunecare si are de regula valori mai mici decat coeficientul de aderenta j

(5.81)

Alunecarea pneului pe calea de rulare

In cazul rotilor echipate cu pneuri transmiterea fortelor tangentiale de tractiune sau franare este insotite de alunecare sau patinare. In procesul de alunecare se disting doua cazuri prezentate in figura 5.26. Daca roata este franata (fig.5.26,a) roata are o miscare cu o turatie mai mica decat cea corespunzatoare vitezei de translatie v, dar aluneca pe calea de rulare. La limita apare situatia blocarii rotii w_R=0. In cazul rotii antrenate (fig.5.26,b) aceasta capata o turatie mai mare decat cea corespunzatoare vitezei de translatie, patinand pe calea de rulare. La limita apare situatia patinarii totale v=0. In ambele situatii s-a depasit aderenta intre pneu si calea de rulare, datorita unei forte tangentiale la roata mai mari decat cea limitata de aderenta.

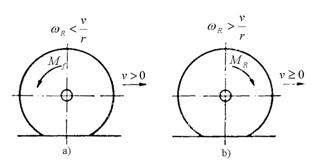
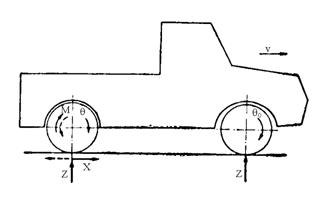
Fig. 5.26. Alunecarea rotii franate si a rotii motoare. Fig.5.27 Rularea rotilor cu alunecare.

Trecerea la alunecarea rotii se poate explica cu ajutorul figurii 5.27, unde se prezinta cazul deplasarii unui autovehicul cu puntea motoare dispusa in spate. Cele doua roti parcurg distante egale s. Roata din fata se rostogoleste cu unghiul q_o, iar roata din spate, incarcata cu momentul M, se rostogoleste cu unghiul q, diferit de q_o. Se considera ca asupra rotii din spate actioneaza un moment de antrenare sau un moment de franare. La variatia reactiunii tangentiale X, datorata modificarii momentului M, se modifica si unghiul q. Acest lucru este pus in evidenta in graficul din figura 5.28, care prezinta dependenta dintre reactiunea tangentiala X si unghiul de rotatie raportat la distanta parcursa.

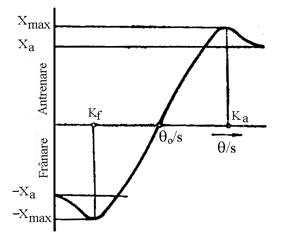
Fig.5.28. Dependenta unghiului de rotatie

specific de reactiunea tangentiala.

La forte tangentiale mici dependenta dintre X si q/s este aproape liniara, valori semnificative ale alunecarii apar dupa ce forta tangentiala a depasit valoarea X_max. La roata antrenata alunecarea incepe sa creasca semnificativ din punctul K_a spre dreapta, iar la roata franata din punctul K_f spre stanga. La alunecarea totala reactiunea tangentiala se reduce la valoare X_a=j_aZ, la roata antrenata se produce patinarea totala caracterizata prin q/s ¥ (fig.5.26,b), iar la roata franata alunecarea totala sau blocarea caracterizata prin q/s 0 (fig.5.26,a). La patinarea totala in cazul rotii antrenate viteza de translatie si spatiul parcurs sunt nule (v=0 si s=0), iar la alunecarea totala in cazul rotii franate viteza unghiulara si unghiul de rotatie sunt egale cu zero (w_R=0 si q

Prin urmare cele doua roti ale autovehiculului prezentat in figura 5.27. desi parcurg acelasi spatiu se rotesc cu unghiuri diferite. Diferenta dintre cele doua unghiuri raportata la unghiul cel mai mare, se numeste alunecare si se noteaza cu a. Astfel raportul:

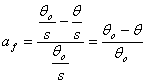(5.82)

reprezinta alunecarea unei roti franate, iar raportul:

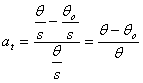(5.83)

reprezinta alunecarea pentru roti motoare.

Deoarece procesul alunecarii este variabil in timp, definirea alunecarii trebuie sa se faca si in functie de variatia unghiurilor de rotire dq si dq_o raportata la deplasarea elementara ds. Pentru alunecarea la franare se obtine relatia:

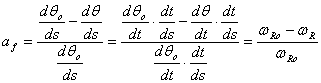, (5.84)

iar pentru alunecarea la transmiterea fortei de tractiune se obtine:

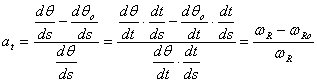, (5.85)

unde w_R este viteza unghiulara a rotii antrenate sau franate de momentul M, iar w_Ro este viteza unghiulara a rotii conduse.

Din conditia de egalitate a vitezelor de translatie pentru cele doua roti obtinem relatia:

(5.86)

unde r_r este raza de rulare a rotii antrenate sau franate si r este raza de rulare a rotii conduse (libere). Deoarece la roata condusa diferenta dintre raza de rulare r si raza dinamica r_d este nesemnificativa egalitatea 5.86 poate fi scrisa sub forma:

(5.86')

Daca in relatiile 5.84 si 5.85 se introduc vitezele unghiulare rezultate din relatia 5.86', se obtine:

(5.87)

Termenul r_dw_R nu reprezinta viteza de translatie a uneia din roti, ci este doar o marime de calcul rezultata din inmultirea vitezei unghiulare w_R a rotii antrenate sau franate cu raza dinamica a rotii conduse.

Inlocuind in relatia 5.87 viteza v din 5.86' se poate exprima alunecarea functie de raza de rulare rr a rotii antrenate sau franate si raza dinamica r_d a rotii conduse:

(5.88)

Trebuie subliniat faptul ca procesul de transmitere a fortelor tangentiale de tractiune sau de franare este insotit in permanenta de alunecare sau patinare, iar prin utilizarea la autovehicule a sistemelor moderne antipatinare sau antiblocare nu se doreste eliminarea patinarii sau a alunecarii ci se doreste mentinerea acestora la valori optime care sa permita atat transmiterea fortelor tangentiale cat si a fortelor laterale necesare ghidarii si mentinerii autovehiculului pe traiectoria comandata de conducatorul auto.

Caracteristica de rulare

Raportul dintre forta tangentiala la roata X si reactiunea normala Z se numeste forta tangentiala specifica si se noteaza cu x, respectiv:

(5.89)

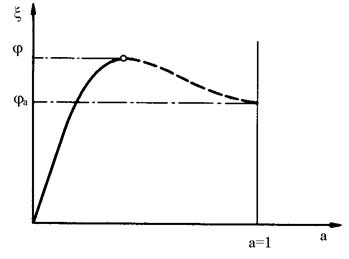Dependenta dintre forta tangentiala specifica x si alunecarea a reprezinta caracteristica de rulare, figura 5.29, care are aproximativ aceiasi variatie atat la antrenarea cat si la franarea rotii. Se observa ca forta tangentiala specifica creste proportional cu alunecarea pana la o anumita valoare a alunecarii, dupa care cresterea este mai redusa pana se atinge valoarea maxima x_max j, dupa care urmeaza o scadere a fortei tangentiale specifice pana la valoarea x j_a pentru a=1.

Fig 5.29. Caracteristica de rulare.

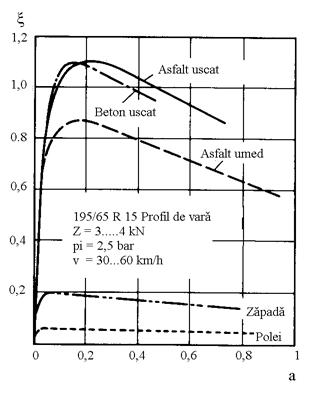
Principalii factori de care depinde caracteristica de rulare sunt: caracteristicile si starea drumului; viteza de deplasare a autovehiculului; marimea sarcinii normale pe roata.

In figura 5.30 sunt prezentate curbele caracteristicii de rulare pentru diferite stari ale drumului. Se observa influenta puternica a starii drumului asupra caracteristicii de rulare, existand variatii mari de la o stare la alta. Valorile maxime ale fortei tangentiale specifice se obtin pentru valori ale alunecarii cuprinse intre 0,1 si 0,25, dar cu cat starea drumului se inrautateste maximele se obtin la valori ale alunecarilor mai mici.

Fig. 5.30. Caracteristica de rulare pentru diferite stari ale drumului.

Influenta vitezei de deplasare asupra caracteristicii de rulare este prezentata in graficul din figura 5.31.

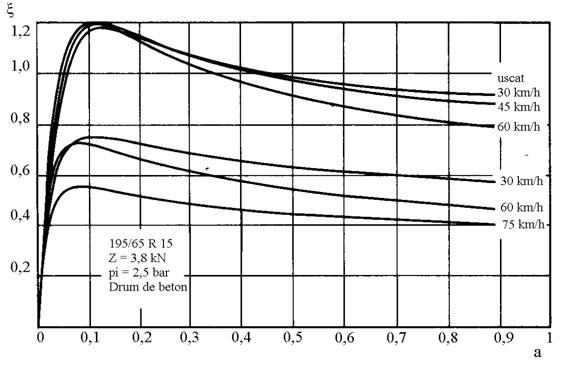
Fig.5.31. Variatia caracteristicii de rulare in functie de viteza.

Influenta vitezei de deplasare vitezei de deplasare asupra caracteristicii de rulare este mai mica pe drumuri uscate decat pe drumuri umede. Reducerea fortei de tractiune specifice cu cresterea vitezei este mai accentuata la valori mai mari ale alunecarii, respectiv la x j_a si mai mica la valorile maxime x_max j

Coeficientul de aderenta

Coeficientul de aderenta j a fost definit prin relatia 5.63, iar cel de frecare de alunecare j_a prin relatia 5.80.

Coeficientul de aderenta tinde sa se identifice cu coeficientul de frecare in cazul soselelor de beton, asfalt, beton asfaltic, deoarece frecarea dintre pneu si calea de rulare reprezinta in acest caz principala cauza a aderentei.

Pe drumuri deformabile sau pe cale de rulare cu macrogeometrie granuloasa a suprafetei, aderenta dintre pneu si calea de rulare se datoreaza si intrepatrunderii proeminentelor pneului cu calea de rulare.

Actiunea reciproca dintre pneu si calea de rulare a format preocuparea multor cercetatori, dintre care o parte considera ca forta de frecare care ia nastere in timpul miscarii autovehiculului este rezultata din insumarea a doi termeni: forta de adeziune de natura moleculara si forta de histerezis, de natura vascoasa. Componenta de adeziune este preponderenta pe o suprafata neteda si uscata, iar componenta de histerezis este preponderenta pe o suprafata rugoasa si umeda.

Cu toate ca influenta aderentei dintre pneu si calea de rulare, asupra parametrilor de miscare ai autovehiculului, nu poate fi reprezentata cu precizie utilizand un singur coeficient, totusi in literatura de specialitate este folosita exclusiv aceasta reprezentare, coeficientul utilizat fiind numit coeficient de aderenta.

Valoarea absoluta a coeficientului de aderenta depinde de foarte multi factori, printre care enumeram: tipul anvelopei, presiunea aerului din pneu, natura si starea caii de rulare, incarcarea rotilor, valoarea alunecarii sau a patinarii, viteza de deplasare a autovehiculului.

In literatura de specialitate sunt prezentate o serie de rezultate ale cercetarilor experimentale pentru determinarea coeficientilor de aderenta in diferite conditii de exploatare functie de diferiti factori de influenta. Datorita complexitatii corelatiilor dintre acesti factori si marimea coeficientului de aderenta, in tabele sunt prezentate valori medii ale acestor coeficienti, in functie de tipul drumului si starea acestuia, ca in tabelul 5.20.

Tabelul 5.20

Valorile medii ale coeficientilor de aderenta.

Fenomenul aderarii pneului de autovehicul la calea de rulare in timpul rularii este de o accentuata complexitate datorita numerosilor factori de influenta variabili, care intervin in timpul rularii rotilor.

Dintre factorii principali care provoaca variatia coeficientului de aderenta pot fi amintiti:

caracteristica suprafetei caii de rulare;

miscarea relativa dintre pneu si calea de rulare;

viteza de deplasare a autovehiculului.

Influenta caracteristicilor suprafetei caii de rulare. In cazul unui pneu de o anumita forma, un anumit desen al benzii de rulare si o anumita presiune interioara, marimea coeficientului de aderenta si variatia acestuia cu viteza de deplasare a autovehiculului depind in mare masura de caracteristicile caii de rulare.

Natura si rugozitatea stratului superficial de acoperire a caii de rulare au o importanta determinanta asupra marimii coeficientului de aderenta. Astfel, excesul de ciment in liantul imbracamintilor de beton, duce la micsorarea porozitatii si ca urmare la reducerea coeficientului de aderenta, fata de cele din beton vibrat.

Starea de umiditate si curatenie a suprafetei de rulare a rotii influenteaza puternic valoarea coeficientului de aderenta, mai ales pe cai cu suprafata neteda, unde apar scaderi ale coeficientului de aderenta cu 30.50%. Suprafetele rugoase, ale caror proeminente produc zone de frecare uscata, sunt favorabile aderentei, in schimb suprafetele netede si lustruite, care mentin o pelicula de apa intre pneu si calea de rulare, au o influenta nefavorabila.

Gradul de umiditate al soselei care se defineste prin grosimea peliculei de apa, face ca valoarea coeficientului de aderenta sa prezinte o variatie mult mai mare decat pe sosea uscata. Astfel in cazul unei sosele din beton cu o buna posibilitate de drenaj pe durata unei ploi moderate (grosimea peliculei de apa nu depaseste cateva zecimi de milimetru), coeficientul de aderenta prezinta variatii mari asa cum se observa din figura 5.32.

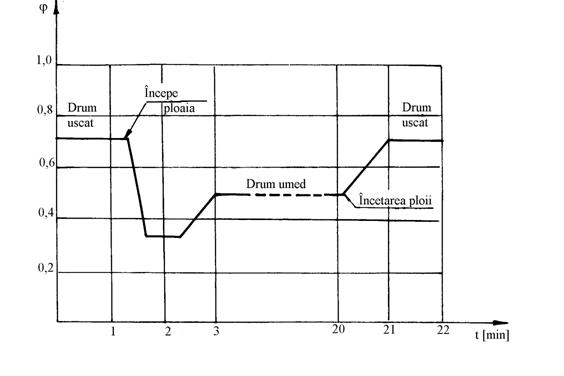
Fig.5.32. Influenta umiditatii caii de rulare asupra coeficientului de aderenta.

Pelicula de murdarie de pe sosea face ca la inceputul umezirii (inceputul ploii) acesteia, coeficientul de aderenta sa scada foarte mult, pentru ca dupa stabilirea unei pelicule de apa curata, coeficientul de aderenta sa creasca la valoarea corespunzatoare unei sosele umede, iar dupa incetarea ploii si uscarea suprafetei soselei, sa revina la valoarea initiala.

In cazul caderilor abundente de apa in cantitati mari, adica pelicula de apa depaseste 1,5 mm, coeficientul de aderenta la anumite viteze de deplasare ale autovehiculului, se poate anula. Acest fenomen este cauzat de eliminarea greoaie a apei de sub pneu si se numeste hidroplanare sau aquaplanare. Hidroplanarea este caracterizata de desprinderea completa a pneului de calea de rulare, contactul dintre pneu si calea de rulare realizandu-se exclusiv prin intermediul peliculei de apa.

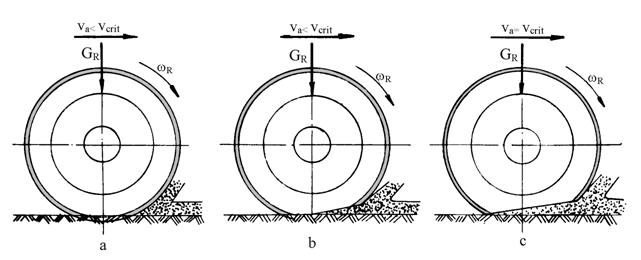
Fig.5.33. Procesul de rulare a pneului pe calea de rulare umeda.

Viteza la care are loc acest fenomen se numeste viteza critica de hidroplanare si depinde in general de grosimea peliculei de apa, de profilul si gradul de uzura a pneului si de presiunea pe suprafata de contact.

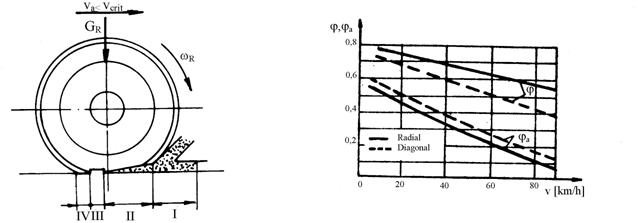
Fig.5.34. Zonarea contactului intre pneu Fig.5.35. Variatia coeficientilor j si j_a in

si calea de rulare umeda. functie de viteza.

Calitativ fenomenul se prezinta ca in figura 5.33. La rularea rotii cu o viteza redusa, pneul poate evacua intreaga cantitate de apa dintre pneu si sosea realizandu-se aderenta (figura 5.33,a). Pe masura ce creste viteza de deplasare a autovehiculului se formeaza o pana de apa intre pneu si sosea (figura 5.33,b), ca apoi la viteza critica pana de apa sa patrunda sub pneu pana ce trece in intregime in partea posterioara a pneului (figura 5.33,c), situatie care conduce la pierderea totala a capacitatii de tractiune, franare si ghidare a pneului.

Daca se analizeaza cazul prezentat in figura 5.33,b, se remarca existenta a patru zone de contact intre pneu si sosea (figura 5.34) si anume: zona I, zona de deviere a peliculei de apa in care predomina efectele inertiale; zona II, care este zona penei de apa in care predomina forta de presiune; zona III, unde se produce distrugerea penei de apa si in care predomina proprietatile vascoase ale apei; zona IV, este zona de contact uscat care asigura aderenta pneului.

S-a constatat de asemenea ca in timpul exploatarii cailor de circulatie, cu acoperiri de beton si beton asfaltic, valoarea coeficientului de aderenta se modifica in timp, in functie de uzura stratului superficial, in sensul ca coeficientul de aderenta scade progresiv, datorita lustruirii rugozitatilor superficiale provocate de uzura treptata a stratului superior al caii de rulare.

In cazul drumurilor deformabile, cresterea coeficientului de aderenta pana la o anumita valoare apare datorita cresterii rezistentei solului dintre pinteni prin indesare. Dupa aceasta limita, coeficientul de aderenta scade, datorita forfecarii si ruperii solului, iar valoarea acestuia este determinata numai de frecarea dintre pneu si solul deformat.

Influenta caracteristicilor pneului Valoarea absoluta a coeficientului de aderenta depinde si de tipul pneului (profil si rigiditate), de presiunea din interiorul pneului si de incarcarea verticala a rotii.

In figura 5.35 sunt prezentate rezultatele incercarilor efectuate in conditii de franare pentru pneuri radiale si diagonale, fiind pusa in evidenta influenta tipului costructiv al pneului asupra coeficientului de aderenta j si asupra coeficientului de frecare la alunecare j_a. Se observa ca la pneurile radiale valorile coeficientilor de aderenta j sunt mai mari decat la pneurile diagonale, iar cele ale coeficientului de frecare la alunecare j_a sunt mai mici. Acest lucru se explica prin faptul ca la pneurile radiale suprafata de contact dintre pneu si calea de rulare este mai mare si presiunea din aceasta zona este repartizata mai uniform.

O importanta deosebita pentru aderenta o are configuratia anvelopei. Astfel, pentru drumuri cu suprafata tare se recomanda anvelope care au crestaturi mici, iar pentru drumurile deformabile se recomanda cele cu crestaturi adanci. Rularea pneurilor cu crestaturi mari pe suprafete tari, este insotita de o aderenta mai scazuta, datorita slabirii periodice a contactului dintre pneu si calea de rulare.

Folosirea anvelopelor cu o coama profilata conduce la un spor de aproximativ 30% a coeficientului de aderenta fata de cel obtinut cu pneuri uzate. Acest lucru este valabil in special pe drumuri umede cand lamelele pneurilor produc zone de frecare uscata, favorabile aderentei, iar canalele dintre profiluri contribuie la evacuarea stratului de apa.

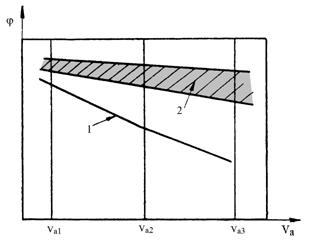
Fig.5.36. Variatia coeficientului de aderenta

functie de profilul pneului si viteza

de deplasare.

Variatia coeficientului de aderenta a pneurilor cu suprafata de rulare profilata (zona 2) si a celor cu suprafata neteda (zona 1), ruland pe o cale umeda, in functie de viteza de deplasare este prezentata grafic in figura 5.36. Se observa influenta puternica a profilelor antiderapante (zona 2) asupra coeficientului de aderenta si asupra variatiei acestuia cu viteza de deplasare.

Rigiditatea pneului, fiind legata de deformatiile acestuia, influenteaza coeficientul de frecare prin histerezis, in sensul ca banda de rulare fabricata din material mai elastic are deformatii mai mari si ca urmare asigura un coeficient de aderenta mai bun.

Modificarea presiunii interioare a aerului din pneu duce la modificarea coeficientului de aderenta, in sensul ca in cazul unui pneu care ruleaza pe o suprafata dura si uscata micsorarea presiunii interioare duce la marirea suprafetei de contact si la scaderea presiunii normale pe cale, fiind insotita de o crestere mica a coeficientului de aderenta.

Pe o cale cu suprafata dura si umeda, cresterea presiunii aerului din interiorul pneului conduce la marirea coeficientului de aderenta datorita sporirii presiunii normale pe calea de rulare si a evacuarii peliculei de apa dintre banda de rulare si calea de rulare.

La rularea rotilor pe drumuri deformabile, pentru marirea coeficientului de aderenta, se recomanda micsorarea presiunii aerului din pneu, lucru care conduce la marirea suprafetei de contact si la imbunatatirea aderentei pneului cu drumul.

Influenta miscarii relative dintre pneu si calea de rulare. In regimul de demarare sau de franare, datorita elasticitatii pneului, zona de contact cu calea de rulare se deformeaza tangential influentand coeficientul de aderenta (figura 5.57) .

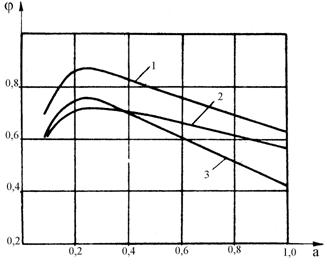
Fig. 5.37. Variatia coeficientului de aderenta

functie de alunecare.

Daca forta de tractiune sau de franare devine prea mare, are loc o patinare sau o alunecare relativa semnificativa a pneului in raport cu calea de rulare. In astfel de situatii, curent intalnite in regimurile de miscare tranzitorie ale autovehiculelor, coeficientul de aderenta variaza substantial cu alunecarea sau patinarea.

Elasticitatea pneului face ca odata cu cresterea alunecarii sau a patinarii pana la circa 20.30%, datorita mariri numarului de elemente de contact cu calea, care lucreaza simultan pe aceasta, sa creasca si coeficientul de aderenta. La cresteri ale alunecarii sau patinarii peste 20.30%, coeficientul de aderenta incepe sa scada, ca urmare a temperaturii din ce in ce mai ridicata dintre pneu si calea de rulare. Marirea temperaturii in zona de contact, la inceput, poate sa duca la cresterea aderentei pe beton sau asfalt, deoarece valoarea lui in acest caz nu mai este determinata de frecarea dintre roata si drum, ci de rezistenta de rupere a cauciucului cu temperatura ridicata.

In figura 5.37 este prezentata variatia coeficientului de aderenta functie de alunecarea a, pentru o cale de beton in trei situatii: uscata (curba 1); umeda (curba 2); murdara si umeda (curba 3).

Fig.5.38. Variatia coeficientului de aderenta

functie de viteza.

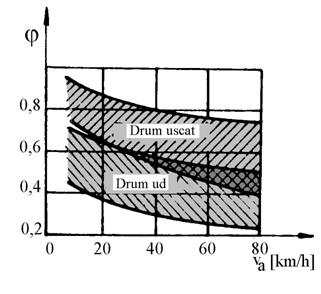
Influenta vitezei de deplasare. Marimea coeficientului de aderenta influentata de factorii prezentati anterior, se reduce simtitor odata cu cresterea vitezei. Aceasta reducere este si mai intensa pe drumuri cu suprafete ude si lunecoase. Astfel, reducerea in acest caz poate atinge 30.50% pentru viteze de deplasare cuprinse intre 20.65 km/h, si este mai putin accentuata la viteze de deplasare mari. Limitele variatiei coeficientului de aderenta pentru diferite tipuri de pneuri pe drumuri de asfalt sau beton, uscate sau ude, sunt prezentate in figura 3.38. Din diagrama se observa ca cresterea vitezei de deplasare a autovehiculului determina o reducere simtitoare a coeficientului de aderenta. Aceasta reducere este mai intensa pe drumuri ude si lunecoase deoarece pelicule de apa nu este evacuata dintre pneu si drum si se ajunge la fenomenul de aquaplanare.

Determinarea coeficientului de aderenta j se face experimental prin metoda franarii unui autovehicul sau a unei remorci dinamometrice.