MISCAREA PLAN - PARALELA A SOLIDULUI RIGID

MISCAREA PLAN - PARALELA A SOLIDULUI RIGID

1. Definitii. Metoda CIR

Un rigid realizeaza o miscare plan - paralela daca trei puncte necoliniare ale acestuia si deci planul determinat de acestea raman tot timpul miscarii intr+un plan fix din spatiu.

Centrul instantaneu de rotatie (CIR=I) este locul geometric al punctelor din planul mobil cu viteza instantanee nula. O proprietate importanta a CIR este aceea ca in raport cu el vitezele tuturor punctelor din planul mobil se determina ca in miscarea de rotatie.

Pentru a se determina acest punct este nevoie de doua elemente si anume:

a)      viteza unui punct al rigidului (modul, directie si sens);

b)      suportul vitezei altui punct al rigidului.

Determinarea CIR se face astfel:

Se ridica perpendiculare pe suporturile vitezelor celor doua puncte in punctele respective (fig. 1). La intersectia acestor perpendiculare se gaseste centrul instantaneu de rotatie (CIR).

1.1. Probleme rezolvate

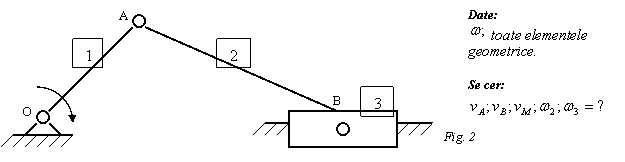
Rezolvare:

Manivela 1 are miscare de rotatie (R), biela 2 are miscare plan - paralela (PP) iar pistonul 3 are miscare de translatie (T).

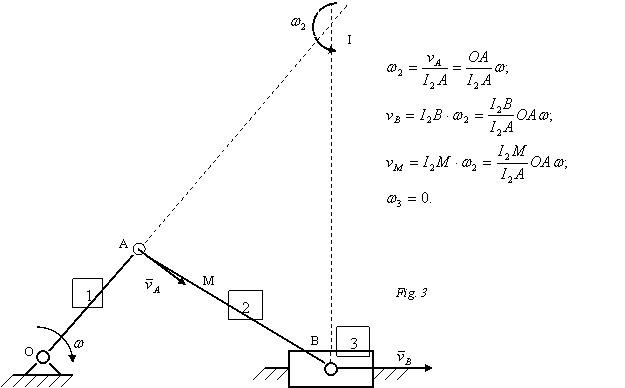
Rezolvare:

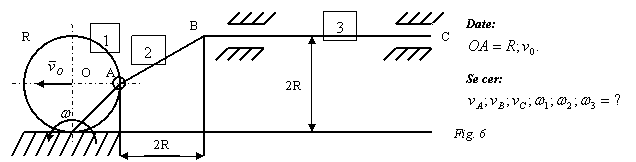
Rezolvare:

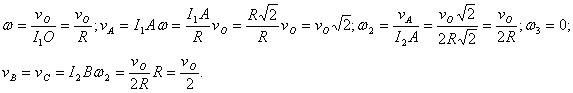
Rezolvare:

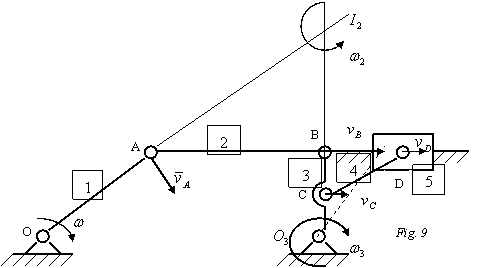
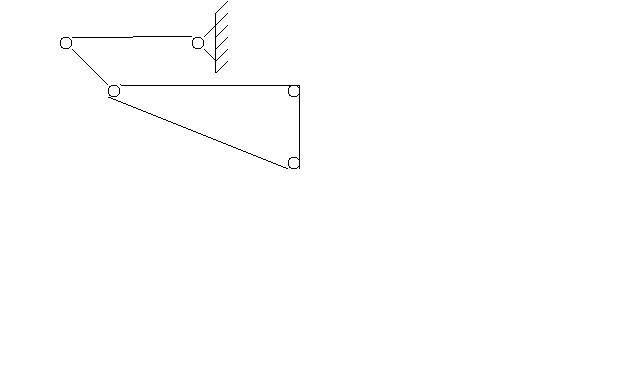
Din figura 8 rezulta ca: elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

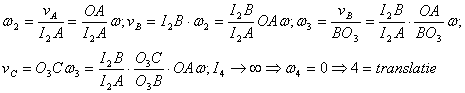
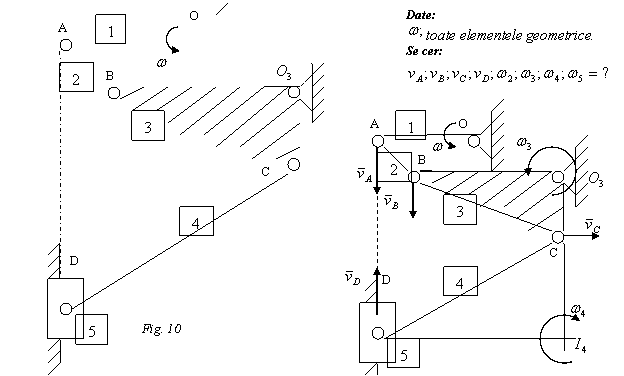
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

1.2. Probleme propuse

Indicatie:

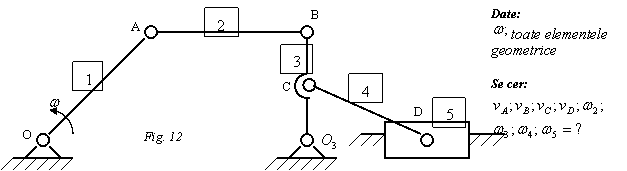
Indicatie:

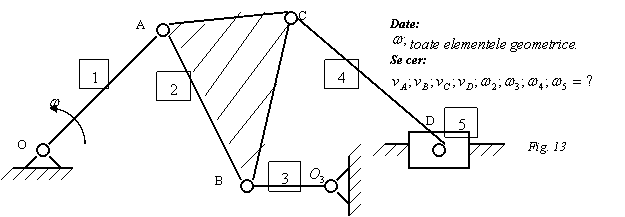
Indicatie:

2. Metoda planului vitezelor si a ecuatiilor vectoriale. Determinarea acceleratiilor

O alta metoda de determinare a distributiei vitezelor pentru un mecanism plan este metoda planului vitezelor si a ecuatiilor vectoriale. Este o metoda grafo - analitica prin care se rezolva grafic ecuatii vectoriale de tip Euler.

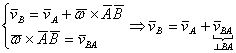
Pe desen, distributia vitezelor se reprezinta la scara cu ajutorul coeficientului de scara pentru viteze:

Pentru determinarea distributiei acceleratiilor se foloseste metoda planului acceleratiilor si a ecuatiilor vectoriale care este, de asemenea, o metoda grafo - analitica prin care se rezolva grafic ecuatii vectoriale de tip Rivals.

Pe desen, distributia acceleratiilor se reprezinta la scara cu ajutorul coeficientului de scara pentru acceleratii:

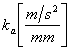
Pentru simplificarea calculelor se considera: k_v=1 si k_a=1.

2.1. Probleme rezolvate

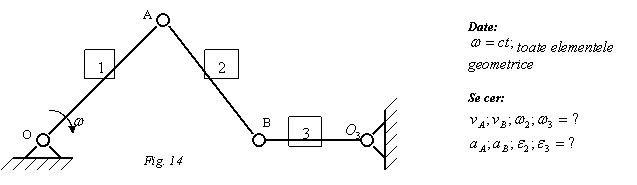
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie.

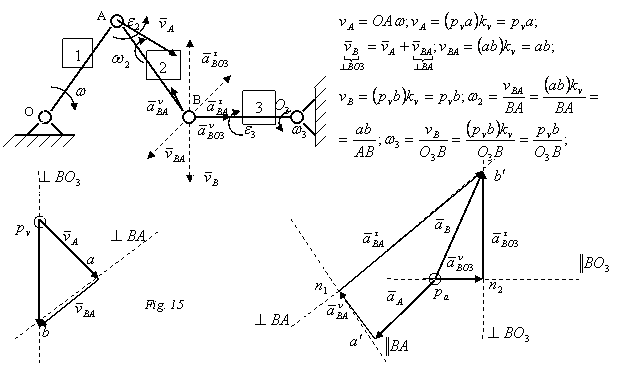
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de translatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

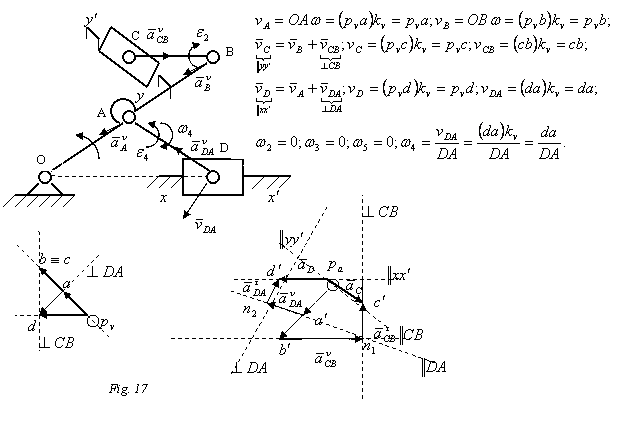
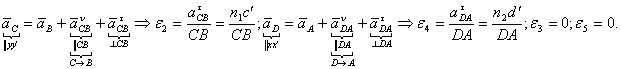
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

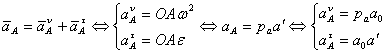
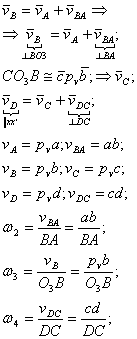
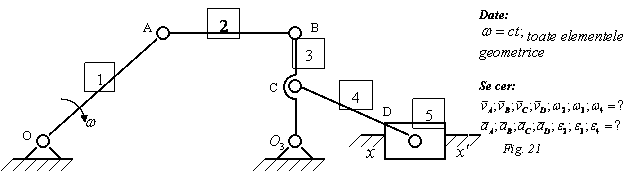
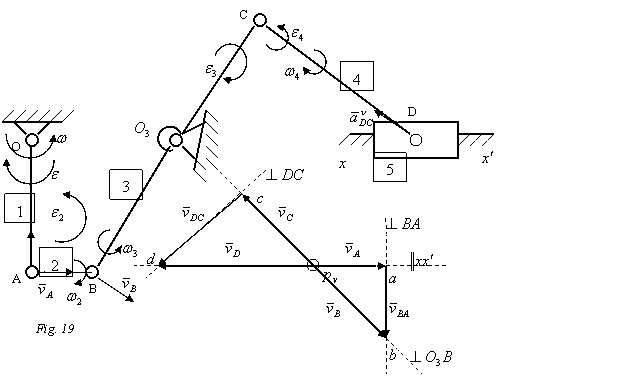
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

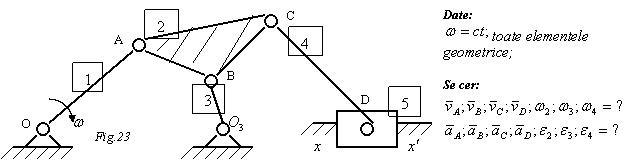
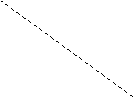
Rezolvare:

Elementul 1 are miscare de rotatie, elementul 2 are miscare plan - paralela, elementul 3 are miscare de rotatie, elementul 4 are miscare plan - paralela, elementul 5 are miscare de translatie.

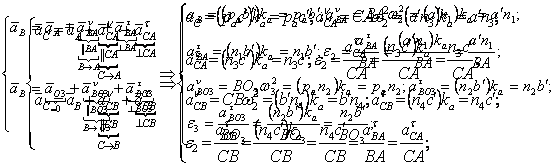
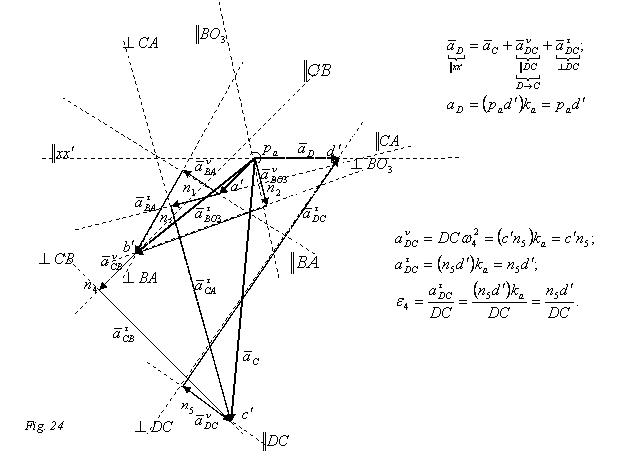
2.2. Probleme propuse

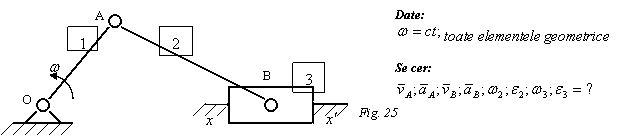
Raspuns:

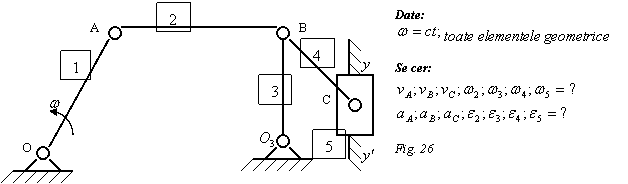
Raspuns:

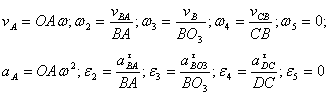
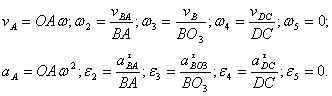
Raspuns:

D

Raspuns:

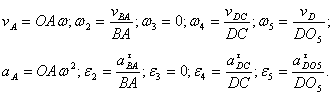
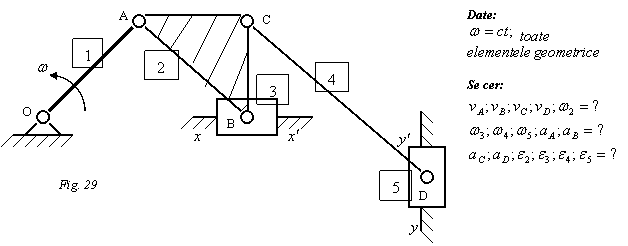
Raspuns: