| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Reprezinta sarcina fundamentala a echipamentului de conducere a unui robot.
1. Problema conducerii unui robot
Conducerea unui robot presupune doua aspecte aparent distincte dar aflate, in realitate, intr-o interdependenta numai principial divizibila.
I).Parcurgerea etapelor unui proces tehnologic presupune deplasarea
dispozitivului de ghidare, in raport cu obiectele din mediu, astfel incat punctul caracteristic sa ocupe, in fiecare etapa, situari impuse sau determinate (acesta este scopul conducerii unui robot).
In fiecare etapa a procesului tehnologic punctul caracteristic trece prin
anumite puncte din spatiul cartezian. Cele mai multe dintre aceste puncte sunt impuse de procesul tehnologic si reprezinta puncte tinta ( goal points). La trecerea punctului caracteristic printr-un punct tinta sistemul de coordonate atasat acestuia are anumite pozitii si orientari care se exprima matricial ( de exemplu cu matricea T6).
Observatii: la trecerea printr-un punct din spatiul cartezian conteaza nu numai
atingerea punctului respectiv, ci si orientarea in spatiu a efectorului final. Conteaza unde si cum "pune mana" robotul.
Orientarile si pozitiile punctului caracteristic ( exprimate cu T6) pot fi calculate
( in blocul pentru modelarea mediului) sau pot fi invatate, inainte de efectuarea deplasarii. Asadar punctele tinta sunt fie invatate, fie calculate.
In deplasarea punctului caracteristic de la un punct tinta la altul, el trece prin puncte via (puncte de trecere). Dintre aceste puncte via unele sunt puncte via propriu-zise ( through via points ), prin care trecerea este obligatorie, iar altele sunt puncte pseudovia, la care trecerea se face numai prin vecinatatea lor.
Observatie: de obicei, in punctele tinta este obligatorie si oprirea, iar prin
punctele via, de regula, trecerea se face fara oprire, cu o anumita viteza impusa. Exista insa si cazuri in care in punctele via este obligatorie si oprirea.
Deoarece punctele definite mai sus se afla in spatiul de lucru al robotului
( impunandu-se trecerea prin ele), este natural ca punctele tinta si via sa fie exprimate in coordonate operationale ( coordonatele in care opereaza efectorul final al robotului). De cele mai multe ori se foloseste exprimarea in coordonate carteziene.
Pornind de la coordonatele operationale ( carteziene) care corespund trecerii
punctului caracteristic printr-un punct tinta sau via, cu analiza cinematica inversa se determina un set de coordonate pozitionale relative ale elementelor cuplelor cinematice conducatoare sau, pe scurt, coordonate c.c.c. numite si coordonate articulare sau coordonate robot.
Acestea pot fi unghiuri θ - pentru cuplele de rotatie - dau distante d - pentru
cuple cinematice de translatie.Setul de valori obtinut ( cu analiza cinematica inversa) este tot un set de puncte tinta sau via, dar exprimate in coordonate c.c.c.(coordonate
articulare, robot).
Conducerea unui robot poate fi realizata in coordonate operationale
(carteziene), cand punctele tinta si via sunt exprimate cu valori numerice concrete pentru elementele matricii T6, sau in coordonate c.c.c., cand punctele tinta si via sunt
exprimate
prin seturi de valori ![]() sau/si dI de la nivelul c.c.c.Se
utilizeaza curent terminologia "conducerea unui robot incoordonateoperationale"
(carteziene), respectiv "conducerea unui robot in coordonate c.c.c." ( coordonate
articulare).
sau/si dI de la nivelul c.c.c.Se
utilizeaza curent terminologia "conducerea unui robot incoordonateoperationale"
(carteziene), respectiv "conducerea unui robot in coordonate c.c.c." ( coordonate
articulare).
II).In afara de trecerea prin punctele tinta si via, in conducerea unui robot
intereseaza si evolutia in timp a miscarii acestuia. In desfasurarea unui proces tehnologic este necesar ca dispozitivul de ghidare sa aiba o miscare lina, fara smucituri, fara franari si/sau accelerari bruste.
Acest deziderat este impus, de cele mai multe ori, de insusi procesul
tehnologic ( de exemplu paletizare, montaj ). Pe de alta parte, o miscare fara smucituri este impusa si de necesitatea de a reduce la minimum uzurile din structura sistemului mecanic.
Evolutia lina in timp se asigura daca pentru coordonata generalizata q se alege o variatie in timp
q = f ( t ) (1)
unde f este o functie lina, adica pentru q se alege o lege de miscare lina.
O functie se numeste lina daca functia si cel putin primele sale doua derivate sunt continue in timp ( uneori se cere ca si derivata a 3-a sa fie continua).
Nota : q este coordonata generalizata utilizata in conducere - poate fi operationala ( carteziana) sau c.c.c.
Concluzie: problema conducerii unui robot consta din doua aspecte intre care exista o stransa legatura : impunerea trecerii prin punctele tinta sau via
( exprimate in coordonate c.c.c. sau in coordonate operationale) in conditiile asigurarii unei evolutii line ( in timp ) a miscarii.
Observatie : Aceasta problema este intalnita si in viata cotidiana la conducerea automobilelor.
In primul rand intereseaza deplasarea automobilului pe drumul impus, cu evitarea obstacolelor. Pe de alta parte, intereseaza ca automobilul sa aiba o evolutie lina, fara accelerari si/sau franari bruste. Deosebirea intre un sofer experimentat si unul incepator se manifesta, mai ales, prin modul in care cei doi asigura evolutia in timp a automobilului.
2. Metode de conducere a robotilor
Metodele de conducere a robotilor se pot clasifica din trei puncte de vedere:
in functie de sursa pentru punctele tinta;
dupa modul de executie a deplasarilor;
dupa coordonatele folosite in conducere.
2.1. Clasificarea metodelor de conducere a robotilor dupa sursa pentru punctele tinta
- conducerea la puncte tinta invatate prin instruire ( programare prin
invatare);
- conducerea la puncte tinta calculate de catre calculatorul ( sau blocul
software) pentru modelarea mediului.
2.2. Clasificarea metodelor de conducere dupa modul de efectuare a deplasarilor
- conducerea secventiala in care se procedeaza la comanda succesiva a
motoarelor de actionare. Metoda se aplica la robotii mai simplii ( mai ales la
manipulatoare).De exemplu, in cazul unui robot T.T.T., cum se arata in fig.1.
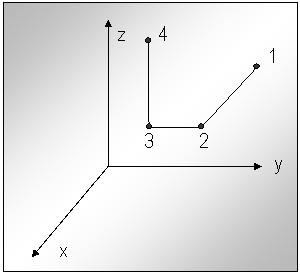
Fig.nr.1. Comanda secventiala a unui robot TTT
O astfel de metoda de comanda are dezavantaj din punctul de vedere al productivitatii mici.
- conducerea punct cu punct sau point to point - PTP . La aceasta
metoda se procedeaza la comanda simultana a tuturor motoarelor de actionare, si daca se poate, toate la viteza maxima. In cazul acestei metode intereseaza numai atingerea punctelor tinta impuse ( cu orientarea aferenta a punctului caracteristic) si nu intereseaza traiectoria descrisa de punctul caracteristic de la un punct tinta la altul.In fig.nr.2. s-au reprezentat cele doua puncte 1-de pornire si 2- de oprire.
Traiectoria descrisa de punctul caracteristic se obtine ca rezultat al miscarilor simultane de pe toate axele. Intrucat traiectoria descrisa de punctul caracteristic este imprevizibila , operatorul uman trebuie sa asigure un spatiu de lucru lipsit de obstacole ( pentru a evita coliziunile).
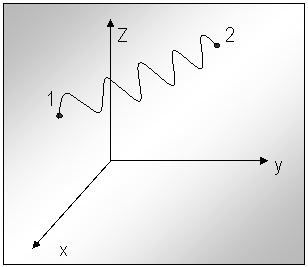
Fig.nr.2.
Comanda PTP
Exemplul clasic de aplicare a acestei metode este sudura in puncte.
- conducerea multipunct - MTP -. Aceasta metoda se aseamana cu metoda PTP, dar robotul invata mult mai multe puncte obligatorii de trecere Pe figura nr. 3. s-au reprezentat mai multe puncte de trecere impuse. Se poate spune ca robotul invata cu aproximatie o traiectorie ( nu chiar strict ) impusa.
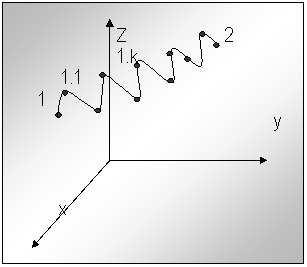
Fig.nr.3. Comanda MTP
Exemplul clasic de aplicare a acestei metode este vopsirea prin pulverizare a unei suprafete.
- conducerea pe traiectorie continua CP (Continuous Path).
Observatie: in literatura de limba engleza exista doi termeni: trajectory si path care in limba romana se traduc la fel, cu traiectorie. Intelesul lor este insa diferit. Prin trajectory se intelege traiectoria spatiala, asociata cu ceilalti parametrii cinematici ai miscarii( viteza, acceleratie). Prin path se intelege strict traiectoria decrisa in spatiu.
2.3. Clasificarea metodelor de conducere dupa coordonatele utilizate
- conducerea in coordonate articulare ( coordonate c.c.c. , coordonate robot). In literatura de limba engleza acest tip de urmarire a miscarilor se numeste joint motion.
In acest caz, din punctele tinta carteziene se calculeaza, cu analiza cinematica inversa, puncte tinta in coordonate c.c.c. Se genereaza miscari line la nivelul fiecarei cuple cinematice conducatoare si se urmareste numai miscarea la nivel articular. Daca miscarile sunt line la nivelul fiecarei cuple cinematice conducatoare, atunci si miscarea per ansamblu este lina.
- conducerea in coordonate carteziene ( coordonate operationale) - cartezian motion in limba engleza .
Miscarea este urmarita la nivelul efectorului final. Sunt necesare multe calcule intrucat miscarea se comanda cu motoarele de actionare amplasate la nivelul cuplelor cinematice conducatoare, iar urmarirea miscarii se face a nivelul efectorului final. De aceea pentru atingerea ( cu precizie) a fiecarui punct din spatiu trebuie efectuata analiza cinematica inversa si analiza cinematica directa de cate 2-3 ori .
Observatie: metodele de conducere prezentate nu trebuie intelese ca metode distincte, utilizate fiecare separat. Dimpotriva, se folosesc asociat cate una dintre metodele apartinand fiecareia dintre grupe.
Exemple:
1). Metoda de conducere pe traiectorie continua si metoda de conducere in coordonate carteziene se folosesc ( impreuna) la sudarea dupa rost. Cele doua metode pot fi asociate fie cu metoda de conducere la puncte invatate, fie cu cea cu puncte calculate;
2). Sudura in puncte a caroseriei unui automobil se face folosind metoda PTP asociata cu conducerea in coordonate c.c.c. la puncte invatate.
3. Traiectorii in miscare
Locul geometric al punctelor din spatiul de lucru al robotului ocupate de punctul caracteristic in timpul deplasarii sale se numeste traiectorie. Suplimentar, in robotica, intereseaza si diferitele orientari pe care le au axele sistemului de coordonate atasat punctului caracteristic in timpul evolutiei pe traiectorie.
Observatie: intereseaza " unde" si " cum" evolueaza efectorul final.
In literatura de limba engleza, pentru traiectorie se utilizeaza doi termeni : path ( urma, trasa) si trajectory. Principial se accepta ca termenul trajectory este utilizat cu un inteles mai larg si anume ca la traiectoria spatiala propriu-zisa se asociaza si alti parametrii cinematici ai miscarii ( viteza, acceleratie).Termenul path presupune numai traiectoria geometric descrisa in spatiu.
Indiferent de modul de conducere al robotului, punctul caracteristic descrie intotdeauna o traiectorie:
in unele cazuri aceasta traiectorie este impusa de procesul tehnologic, caz in care se efectueaza conducere CP - pe traiectorie carteziana continua;
in alte cazuri traiectoria descrisa nu este impusa, fiind impuse numai punctele ce trebuie atinse. La trecerea de la un punct tinta la altul ( se comanda simultan motoarele de actionare) punctul caracteristic descrie o traiectorie oarecare. Se obtine o traiectorie ca rezultat al miscarilor de la nivelul fiecarei cuple cinematice conducatoare.
Legatura spatiu-timp in miscarea unui robot
In conducerea unui robot intereseaza:
trecerea prin anumite situari impuse sau calculate;
evolutie lina in timp.
In conducere se procedeaza la comanda coordonatei generalizate catre valori diferite, in momente diferite. In acest scop, pentru coordonata generalizata q se alege legea de miscare
q = f( t ) (1)
unde f(t) este o functie de timp lina, ceea ce inseamna ca functia si primele sale doua derivate sunt continue.
Legatura intre spatiu si timp se realizeaza prin aceea ca, la anumite valori pentru timp, valorile numerice ale lui f( t ) trebuie sa fie egale cu valorile lui q corespunzatoare unor puncte tinta si via de pe traiectorie.
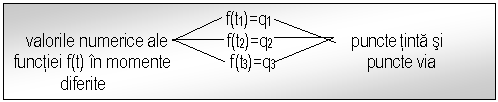
Exemple de legi de miscare
a). - miscarea start - stop.
Fig.nr. 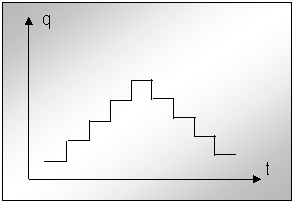
Miscarea start-stop
b). - evolutie liniara pe portiuni.
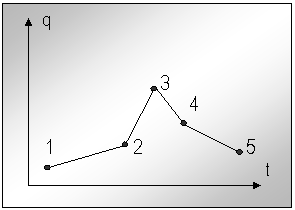
Fig.nr.5.
Miscare cu viteza
constanta pe
portiuni
O evolutie liniara intre doua puncte tinta sau via inseamna deplasare cu viteza constanta intre doua puncte:
![]() q=kt+n
q=kt+n ![]() =k
=k
Se observa ca in punctele tinta si via are loc o schimbare brusca a pantei dreptei, adica o schimbare brusca a vitezei. O astfel de miscare este foarte simpla, dar este neconvenabila deoarece determina aparitia de socuri.
c). - evolutie liniara.
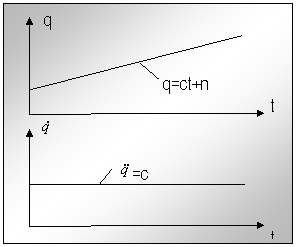
Fig.nr. 6.
Miscare cu aceeasi
viteza constanta
O astfel de miscare presupune deplasarea cu aceeasi viteza constanta pe
tot parcursul. Este principial utilizabila in conducerea unui robot, dar
prezinta dezavantajul ca pornirea se face brusc cu viteza ![]() =const., ceea ce ar presupune o acceleratie
=const., ceea ce ar presupune o acceleratie ![]() =
=![]() in punctul de start.
in punctul de start.
Astfel de acceleratii nu se pot obtine practic pentru ca partile mecanice miscate au masa finita si in momentul accelerarii apar forte de inertie carora li se opun forte elastice. In final rezulta deformari in mecanism.
In consecinta, in realitate, pentru viteza se obtine o variatie de forma prezentata in fig.7.
Fig.nr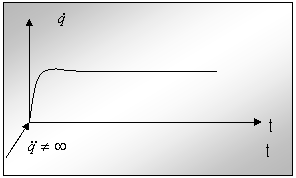
Profilul
de viteza
realizabil
practic
d). - evolutie dupa profil trapezoidal de viteza.
Pornind de la observatia ca nu se poate realiza o deplasare cu viteza constanta pe tot parcursul, in conducerea unui robot nu se foloseste aceasta metoda, ci se alege pentru viteza o variatie trapezoidala ,ca in fig.8.
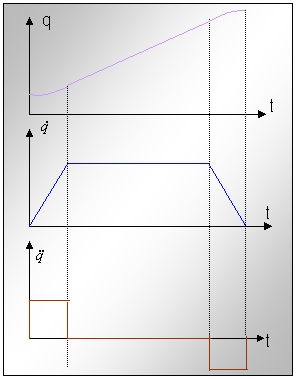
Fig.nr.8.
Evolutie
dupa un profil
trapezoidal
de viteza
Aceasta metoda este frecvent folosita in conducerea unui robot si a fost denumita conducere dupa profil trapezoidal de viteza.
Observatie: exemplele de miscare prezentate mai sus constituie si cele mai simple metode de conducere folosite la roboti.
5. Legatura spatiu-timp in descrierea unei traiectorii
Fie un exemplu de traiectorie liniara intr-un plan cartezian (fig.9) :
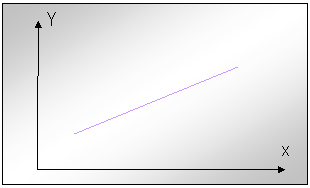
Fig.nr.9. O dreapta oarecare in plan
Ecuatia dreptei este y = m x+ n (2.)
unde:
- m este panta dreptei
- n este taietura dreptei.
Prin derivare:
![]() (3)
(3)
Procedand la impartire cu dt atat la numitor cat si la numarator :
![]()
![]() (4)
(4)
Presupunand ca aceasta dreapta trebuie descrisa intr-un plan de punctul caracteristic, iar acesta se misca cu viteza constanta dupa directia axei coordonatei x si tot cu viteza constanta dupa directia axei coordonatei y, iar raportul celor doua viteze este m, punctul caracteristic va descrie in plan o dreapta de panta m.
Continuand rationamentul: 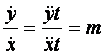 (5)
(5)
Daca cele doua miscari dupa directia axelor de coordonate sunt uniform accelerate, iar raportul acceleratiilor este m, atunci in plan se descrie o dreapta de panta m.
Adica daca pe fiecare dintre axele Ox si Oy se alege cate o lege de miscare:
![]() (6)
(6)
si 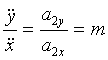 (7)
(7)
atunci in plan este descrisa o dreapta.
Observatie : in exemplul considerat s-a constatat ca urmarind o anumita evolutie in timp se obtine o anumita forma a traiectoriei din spatiul cartezian.
Din punct de vedere practic, realizarea unei drepte in plan se obtine alegand portiuni cu miscare uniform accelerata si portiuni cu miscare rectilinie uniforma.
Fie o dreapta in plan ce se presupune a deveni o traiectorie impusa (fig.10.)
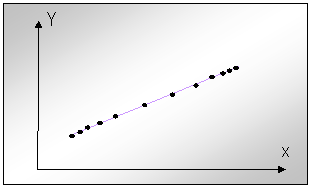
Fig.nr.10 Puncte alese pe o traiectorie liniara
Pe aceasta dreapta se aleg mai multe puncte tinta si via. In mod intentionat la inceputul si sfarsitul parcurgerii dreptei se aleg puncte amplasate mai des, iar pe mijlocul liniei se aleg puncte amplasate mai rar. Pentru descrierea acestei drepte, in miscare, este necesar ca la inceputul si sfarsitul trasarii ei miscarea dupa x si y sa se efectueze uniform accelerat cu:
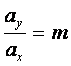 (8)
(8)
unde m este panta dreptei.
pe portiunea din mijloc se impune ca miscarea sa se efectueze cu viteze constante:
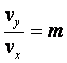 (9)
(9)
iar la sfarsitul dreptei miscarile se fac uniform incetinit cu :
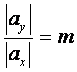 . (10)
. (10)
Deci daca se conduce robotul dupa un profil trapezoidal de viteza, dupa fiecare dintre axele x si y, atunci in plan punctul caracteristic descrie o dreapta cu panta :
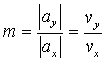 (11)
(11)
Observatii :
1). Pe portiunile de accelerare si decelerare punctele de pe dreapta nu sunt echidistante in spatiu, dar sunt echidistante in timp. Adica spatiul parcurs intre un punct si altul ( pe portiunile de accelerare) este diferit, dar intervalul de timp intre ele este acelasi.
2). Pe fiecare dintre coordonatele x si y se alege cate o lege de miscare cu profil trapezoidal de viteza, cu:
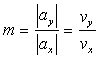 ,
,
iar in spatiu se traseaza o dreapta de panta m.
3). Situatia se poate generaliza si in spatiul tridimensional pentru trasarea unei drepte in spatiu.
4). O astfel de metoda de conducere este direct aplicabila in cazul unui robot T.T.T.
5). Legile de miscare rectilinie uniform accelerata:
![]() (6)
(6)
si rectilinie uniforma:
![]() (12)
(12)
sunt functii line ( functia si primele sale doua derivate sunt continue), deci miscarea per ansamblu este lina.
6). In cazul unui robot diferit de configuratia T.T.T. metoda se aplica mai greu deoarece :
o deplasare cu ![]() constante nu inseamna
implicit si o deplasare cu v=ct. si a =ct. la nivelul fiecarui motor amplasat
la cate o cupla cinematica conducatoare. In general vitezele si acceleratiile
pe x si y si cele de la nivelul fiecarei cuple cinematice conducatoare se
stabilesc cu Jacobianul.
constante nu inseamna
implicit si o deplasare cu v=ct. si a =ct. la nivelul fiecarui motor amplasat
la cate o cupla cinematica conducatoare. In general vitezele si acceleratiile
pe x si y si cele de la nivelul fiecarei cuple cinematice conducatoare se
stabilesc cu Jacobianul.
panta m a dreptei este impusa de traiectoria dorita si nu intotdeauna se pot sintetiza si practic viteze de valori astfel incat raportul lor sa fie chiar m. De cele mai multe ori se admite deplasarea cu viteze aflate intr-un raport cat mai apropiat de m si se accepta o anumita abatere de la dreapta impusa.
De multe ori, impunand anumite
valori ale vitezei pe axele x si z si efectuand calculul cu Jacobianul pot
rezulta viteze![]() , la nivelul cuplelor cinematice conducatoare,
nerealizabile fizic. In aceasta situatie se alege, la nivelul fiecarei cuple
cinematice conducatoare, cea mai apropiata valoare realizabila fizic pentru
viteza si se sintetizeaza deplasari cu aceste viteze rezultand o traiectorie
numai aproximativ exacta.
, la nivelul cuplelor cinematice conducatoare,
nerealizabile fizic. In aceasta situatie se alege, la nivelul fiecarei cuple
cinematice conducatoare, cea mai apropiata valoare realizabila fizic pentru
viteza si se sintetizeaza deplasari cu aceste viteze rezultand o traiectorie
numai aproximativ exacta.
Concluzii : metoda descrisa este direct aplicabila pentru o structura de mecanism T.T.T., este deosebit de utila pentru intelegerea legaturii spatiu-timp in conducerea unui robot, dar se aplica mai greu in cazul altor tipuri de roboti.
6_Legatura spatiu-timp prin ecuatii parametrice
Observatie: pentru simplificare vom arata aceasta legatura in cazul unei traiectorii liniare plane.
Ecuatia unei drepte in plan este:
![]() (2)
(2)
unde: m este panta dreptei ,iar n este taietura. Aceasta este forma explicita de scriere .
In geometria analitica se cunosc si alte forme de reprezentare a ecuatiei unei drepte. Dintre acestea ne intereseaza ecuatiile parametrice ale dreptei:
![]()
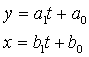 (13)
(13)
unde t este un parametru arbitrar scalar.
Observatie: eliminand t din sistemul (13) se ajunge la forma ecuatiei (2) pentru dreapta.
La fel, se poate scrie si un sistem de ecuatii de gradul 2 :
![]()
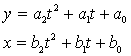 (14)
(14)
sau:
![]()
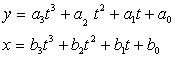 (15)
(15)
, s.a.m.d.
Observatie: se pot scrie si forme cu ecuatii de grad mai mare, singura conditie, in cazul dreptei, fiind aceea ca cele doua ecuatii trebuie sa fie de acelasi grad.
Astfel de ecuatii parametrice exista si pentru alte curbe din plan si spatiu
( sinusoida, curba lantisor, cerc, elipsa, parabola, hiperbola,.).
In general, o curba in spatiu se exprima prin sistemul de ecuatii:
![]()
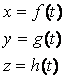 (16)
(16)
unde f, g si h sunt functiile parametrice ale curbei, iar t este un parametru scalar arbitrar.
Sistemul (16) este sistemul de ecuatii parametrice ale curbei.
Pentru o dreapta functiile f, g si h sunt de acelasi grad, iar pentru traiectorii de alte forme, au grade diferite.
Pornind de la aceste cunostinte din geometria analitica, in robotica se alege ca parametru scalar t chiar timpul, pentru ca in robotica intereseaza evolutia in timp a miscarii.
Observatii
1). Functiile parametrice sunt intotdeauna polinomiale si, prin urmare, sunt functii line;
2). Daca scalarul t este timpul, atunci functiile parametrice sunt si legi de miscare dupa coordonatele carteziene.
7. Functii conducere
Pornind de la ecuatiile parametrice ale unei curbe si de la faptul ca se impune ca deplasarea sa se efectueze lin, in robotica se folosesc ecuatiile parametrice ale unei curbe in care variabila scalara este timpul.
Observatia in legatura cu ecuatiile parametrice ale unei curbe poate fi generalizata. Cele trei forme de exprimare ale unei curbe in spatiu sunt:
![]() forma implicita. (17)
forma implicita. (17)
![]()
![]()
![]() forma explicita. (18)
forma explicita. (18)
![]()
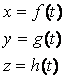 forma cu ecuatii
parametrice. (16)
forma cu ecuatii
parametrice. (16)
O curba in spatiu poate fi insa exprimata si in alte coordonate decat cele carteziene x, y, z. Fie acestea coordonatele generalizate:
q i ; i =1,.,n. (19)
In acest caz ecuatia curbei respective poate fi exprimata fie in forma implicita:
![]() (20)
(20)
fie cu sistemul de ecuatii parametrice:
![]() , i = 1,.,n. (21)
, i = 1,.,n. (21)
Aplicand aceasta observatie la robotica, pentru o anumita traiectorie a punctului caracteristic, putem folosi exprimarea acesteia cu sistemul de ecuatii parametrice:
![]() , i = 1,.,n,
, i = 1,.,n,
dar cu particularitatea ca:
a). se alege ca parametru scalar t timpul;
b). coordonatele generalizate qi se
aleg chiar coordonatele cuplelor
cinematice conducatoare ale robotului (unghiuri ![]() sau deplasari di,
dupa felul cuplelor cinematice);
sau deplasari di,
dupa felul cuplelor cinematice);
c). se aleg toate functiile f i ( t ) functii line.
Aceste
functii ![]() au fost numita in
robotica functii conducere.
au fost numita in
robotica functii conducere.
Observatii
1). Functiile de conducere sunt de fapt:
a). functiile parametrice ale traiectoriei;
b). legile de miscare de la nivelul cuplelor cinematice conducatoare.
2). Denumirile " functiile parametrice ale traiectoriei" sau "legile de miscare de la nivelul cuplelor cinematice conducatoare" sau "functiile conducere de la nivelul cuplelor cinematice conducatoare" inseamna acelasi lucru.
8. Etapele de realizare a conducerii unui robot
Conducerea unui robot se desfasoara in trei etape:
1). specificarea miscarii;
2). generarea miscarii;
3). conducerea nemijlocita a elementelor cuplelor cinematice
conducatoare.
8.1. Specificarea miscarii.
In vederea realizarii miscarilor de catre robot, acestea trebuie specificate, explicitate. In etapa de specificare se aleg functiile conducere ( de timp) si se impune conditia ca, la anumite momente, functiile conducere sa ia anumite valori( la momente impuse functiile conducere sa ia valorile impuse de punctele tinta sau via).
Din aceste conditii se calculeaza valorile concrete pentru coeficientii numerici din functiile conducere.
Exemplu : pentru realizarea unei drepte in plan se aleg, pentru evolutia dupa coordonatele carteziene, legile de miscare ( functiile conducere):
![]()
![]()
![]() (13)
(13)
Procesul tehnologic impune ca in descrierea dreptei la un moment t0 sa se treaca prin punctul de coordonate (x1, y1), iar la momentul tf prin punctul (x2,y2).
![]()
![]() t0 (x1,y1) tf (x2,y2). (22)
t0 (x1,y1) tf (x2,y2). (22)
In plus mai sunt impuse conditiile:
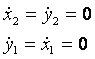 (23)
(23)
adica miscarea sa porneasca din repaos si sa se opreasca in punctul final.
Inlocuind t0 = 0 si impunand x(t0) = x1 si y(t0) = y1, respectiv x(tf) = x2 y(tf) = y2 si adaugand ( eventual) conditiile de viteza se obtine un sistem de ecuatii cu patru necunoscutele: a0, a1, b0, b1 care se rezolva si se obtin coeficientii functiilor conducere.
Concluzie: specificarea miscarii consta in alegerea functiilor conducere si calculul coeficientilor din expresia lor.
Observatie: In principiu, specificarea miscarii se face off-line, adica se efectueaza inainte de demararea propriu-zisa a miscarii.Calculul off-line este posibil cand miscarea care urmeaza a fi efectuata este pe deplin cunoscuta pentru procesul tehnologic respectiv.In cazul proceselor tehnologice flexibile in care etapele depind de evenimentele produse anterior, pot sa apara situatii cand specificarea trebuie efectuata online. In aceste cazuri specificarea se face, totusi, cu cateva momente in avans.
Pentru functiile conducere in literatura de specialitate sunt date si cateva cerinte suplimentare :
- sa fie functii line;
- sa fie cat mai simple ( ca expresie);
- sa asigure un timp de calcul cat mai scurt;
- sa nu necesite iteratii de calcul;
- sa aiba corespondent fizic in miscare, adica sa se evite
miscarile " hoinare" ale robotului ( wanderer = hoinar, in
engleza).
8.2. Generarea miscarii. Generatorul de traiectorie ( GT ).
A doua etapa este cea in care se genereaza, prin calcul, punctele traiectoriei ce trebuie descrisa in miscare. In sistemul de conducere al unui robot exista un bloc (calculator independent sau o subrutina software) dedicat care se numeste generator de traiectorie ( trajectory planner) GT. Acest bloc calculeaza fie in coordonate carteziene, fie in coordonate c.c.c., valorile numerice discrete pentru functiile conducere la intervale constante de timp - cuprinse de regula intre 1/200 Hz si 1/20 Hz ( in functie de viteza calculatorului).
Aceste valori numerice corespund unor pozitii succesive in spatiu pe care le ocupa elementele D.G. In acest mod, GT calculeaza, pe baza functiilor conducere, locatiile succesive in care trebuie sa se situeze in timp dispozitivul de ghidare, realizand de fapt corespondenta spatiu-timp in miscare.
Se asigura concomitent trecerea prin punctele tinta si via impuse si o deplasare lina, fara socuri.
Schematic, blocul generator de traiectorie se reprezinta ca in fig.11.
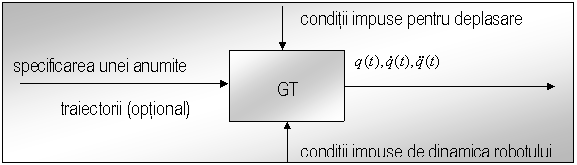
Fig.nr.11. Schema bloc a generatorului de traiectorie
GT primeste ca date de intrare conditiile impuse pentru deplasare si cele impuse de dinamica sistemului mecanic ( in unele cazuri primeste chiar expresia analitica a unei traiectorii carteziene pe care punctul caracteristic trebuie sa o descrie in spatiu).
La iesirea GT se obtin, cu o frecventa cuprinsa intre 20 Hz si 200 Hz, pozitii, orientari, acceleratii, in coordonate carteziene sau c.c.c., care sunt impuse succesiv, pentru deplasarea elementelor mecanice.
Pentru generatorul de traiectorie se cunosc doua moduri de operare :
a) fara sintetizarea unei traiectorii carteziene prescrise;
b) cu sintetizarea unei traiectorii carteziene impuse de procesul tehnologic.
In primul caz, pentru deplasarea elementelor mecanice, conform secventei de parametrii calculati de generatorul de traiectorie, punctul caracteristic descrie in spatiu o traiectorie obtinuta ca si rezultat al miscarilor pe toate axele ( o traiectorie greu de exprimat analitic si greu de urmarit vizual).
In modul a) de operare GT primeste ca si conditii impuse punctele tinta si via si forma aleasa pentru functiile conducere. In etapa de specificare a miscarii generatorul de traiectorie calculeaza coeficientii variabilei timp, din conditiile impuse. In etapa de generare a miscarii GT genereaza la intervale de timp constante ( c.c.c sau coordonate carteziene , viteze, acceleratii , necesare pentru deplasarea robotului, conform conditiilor impuse si dupa functiile conducere alese.
In modul b) de operare generatorul de traiectoriie primeste la intrare si expresia analitica a unei traiectorii carteziene impuse de procesul tehnologic. Daca traiectoria este complicata expresia ei se obtine prin aproximarea acesteia pe portiuni cu segmente de curbe simple ( dreapta, cerc, parabola,.).
Pozitiile obtinute din functiile conducere trebuie sa coincida sau sa aproximeze cat mai precis punctele traiectoriei carteziene impuse.
Indiferent de modul de operare adoptat, a sau b, pentru GT, marimile de la iesirea sa reprezinta marimi de prescriere pentru regulatoarele automate din structura sistemelor de conducere locale ce compun sistemul de actionare al robotului. Sistemele de conducere locale asigura conducerea nemijlocita a elementelor cuplelor cinematice conducatoare.
8.3. Conducerea nemijlocita a elementelor cuplelor cinematice
conducatoare
Observatie : termenul nemijlocit are ,in acest context, semnificatia direct, fara intermediari.
Indiferent de modul de conducere al robotului, miscarile elementelor sistemului mecanic se provoaca la nivel articular. Analizand schema bloc a echipamentului de conducere a unui robot (fig.2.1) se constata ca sistemul de actionare al acestuia se compune din mai multe sisteme de conducere locala
( SCL), construite cu o structura de sistem cu reglare automata ( SRA)(vezi si fig.12)
Elementul central al cate unui sistem de conducere local este motorul de actionare care produce miscarile elementelor cuplelor cinematice conducatoare.
Observatie: motorul poate fi electric, hidraulic, pneumatic sau mixt, dupa caz; in functie de tipul motoarelor folosite si robotul fiind denumit cu actionare electrica, hidraulica, pneumatica sau mixta.
Motorul este alimentat cu energie de la o sursa de alimentare ( reteaua de alimentare cu curent alternativ, un agregat hidraulic, reteaua de aer comprimat). Intre sursa de alimentare si motor se afla etajul electronica de putere, EP, cu rolul de a amplifica , pana la nivelul de putere corespunzator, comenzile catre motor.
Conducerea fiecarui sistem de conducere local este asigurata de un microprocesor sau microcontroler numit controler de ax (care coordoneaza SCL).
Observatie: in unele cazuri se utilizeaza microprocesosoare sau microcontrolere mai performante si se foloseste un singur microprocesor sau microcontroler pentru comanda mai multor SCL (de regula, maxim trei).
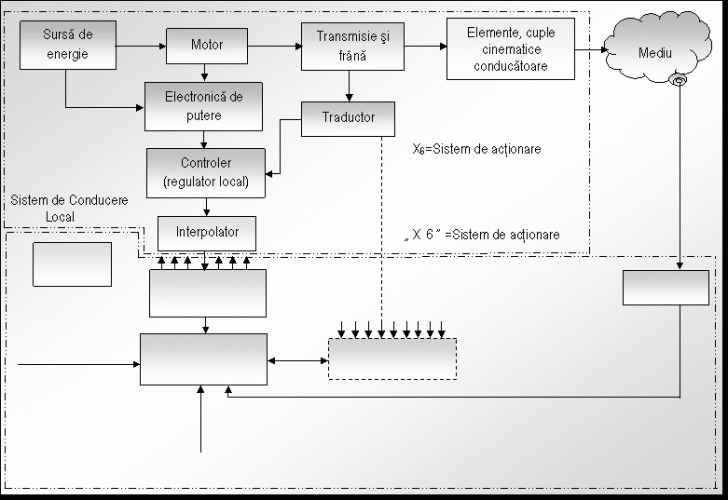
Fig.nr.12. Schema bloc a unui sistem de conducere locala (de inlocuit desenul cu SRA/SCL)
Fiecare cupla cinematica conducatoare este condusa de catre un SCL.
Miscarile elementelor cuplelor cinematice conducatoare sunt urmarite de traductoare de pozitie, viteza, acceleratie, care fac parte din structura sistemelor de conducere locale, si furnizeaza fiecarui controler de ax informatiile cu privire la miscarea efectuata in realitate de elementele mecanice.
8.3.1.Problema conducerii nemijlocite a elementelor cuplelor
cinematice conducatoare.
1).Generatorul de traiectorie furnizeaza ( in unele cazuri prin intermediul interpolatorului) pozitia impusa qd ( in unele cazuri si/sau viteza impusa si/sau acceleratia impusa) numita marime de prescriere.
2). Traductorul
furnizeaza marimile atinse in realitate de elementele mecanice: ![]() , numite marimi de
reactie.
, numite marimi de
reactie.
3). Controlerul de ax calculeaza abaterea ( numita uneori si eroare).
 (24)
(24)
4). Abaterea se introduce intr-o formula numita algoritm de reglare, AR, proiectat de inginerii automatisti, care permite calcularea unei marimi de comanda y cu care apoi se comanda electronica de putere si in final, motorul. y rezulta din calcule astfel incat comanda motorul in sensul anularii abaterii.
Observatie: operatiile 3 si 4 sunt efectuate de controlerul de ax.
Algoritmul de reglare este proiectat astfel incat sa implementeze o anumita lege de reglare. Principalele legi de reglare sunt:
reglarea de tip P ( proportional) in care marimea de comanda y este proportionala cu abaterea;
reglare de tip PI ( proportional integratoare) in care y este proportionala cu abaterea si cu integrala ei;
reglarea de tip PID ( proportional integrator derivativa) in care y e proportionala cu abaterea, integrala si derivata ei.
Fiecare dintre aceste legi de reglare prezinta avantaje si dezavantaje si se utilizeaza in functie de performantele urmarite in reglare.
Principalele performante pretinse de la un algoritm de reglare sunt:
- timp de raspuns cat mai scurt;
- eroare nula in regim stationar;
- evitarea intrarii in stare de oscilatie.
La proiectarea algoritmului de reglare se tine seama de parametrii elementelor componente sistem ( masele puse in miscare, constantele motorului de actionare, parametrii etajului de electronica de putere).
Observatie : In capitolul se va prezenta mai detaliat problematica reglarii automate.
5) Comanda, cu semnalul y, blocul electronica de putere si,prin aceasta,motorul determinand,in final miscarea elementelor mecanice in sensul anularii abaterii.
Fiecare articulatie este prevazuta cu cate un sistem de conducere local propriu si deci, conducerea nemijlocita a axelor unui robot se efectueaza intr-un mod independent pentru fiecare cupla cinematica conducatoare.
Observatie: ideal ar fi ca la nivelul intregului robot sa se urmareasca simultan toate miscarile de pe toate axele si sa se infaptuiasca o conducere in ansamblu a robotului cu un, eventual, regulator global. Acest lucru nu se poate realiza momentan pentru ca:
nu exista traductoare carteziene de mare precizie la preturi convenabile ( pretul unui astfel de traductor este comparabil cu cel al intregului echipament electronic al robotului);
legaturile dintre miscarile pe diferite axe sunt exprimabile cu ecuatii complicate
( neliniare) si timpul de calcul necesar conducerii ar creste exagerat de mult
( conducerea in timp real devine imposibila).
9. Conducerea unui robot in coordonate c.c.c.
Aceasta metoda de conducere este frecvent utilizata in conducerea unui robot. Miscarea elementelor mecanice este urmarita la nivel articular, adica la nivelul fiecarei cuple cinematice conducatoare individuale. Este vorba de conducerea in coordonate c.c.c. sau in coordonate robot.
In literatura de limba engleza terminologia folosita este joint motion ( joint inseamna articulatie).
Si in acest caz punctul caracteristic, in miscarea respectiva, descrie o traiectorie. Aceasta este insa obtinuta ca rezultat al miscarii simultane pe toate axele ( uneori nu pe toate axele). De cele mai multe ori traiectoria rezultata este complicata, greu de urmarit vizual si are o expresie analitica complicata.
9.1.Specificarea miscarii in coordonate c.c.c.
In cazul acestei metode specificarea miscarii presupune parcurgerea mai multor etape:
a). Determinarea punctelor tinta si via in coordonate c.c.c.
in cazul in care robotul a fost invatat prin instruire (programat prin invatare), cazul robotilor simpli, punctele tinta si via sunt memorate in coordonate c.c.c. De aceea aceasta etapa, in acest caz, nu presupune decat preluarea din memorie a punctelor invatate;
pentru robotii evoluati, la care modelarea mediului se face prin calcul, se calculeaza matricile T6 pentru fiecare etapa a procesului tehologic si, cu analiza cinematica inversa, se determina punctele tinta in coordonate c.c.c.
b). Determinarea timpilor de deplasare
Dupa ce punctele tinta pentru elementele cuplelor cinematice conducatoare se cunosc, se observa ca vitezele maxime realizabile la nivelul fiecarei axe sunt , de asemenea, cunoscute; masele care trebuie miscate si rezistentele ce trebuiesc invinse se stiu( P=F v, iar puterea P se cunoaste pentru fiecare motor).
Intr-o prima etapa, se considera ca elementele fiecarei articulatii se deplaseaza cu viteza maxim posibila. Cu aceste viteze se calculeaza timpul minim pentru deplasare:
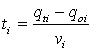 , unde i =
1,.,6 (25)
, unde i =
1,.,6 (25)
si :
- qoi este punctul initial;
- qfi este punctul tinta final;
- vi este viteza maxim realizabila;
- i este cupla cinematica numarul i.
Pentru elementele fiecarei axe se cunosc si acceleratiile maxim obtenabile si deci se pot calcula timpii tacci de accelerare de la 0 la vi , repectiv de deccelerare de la vi la 0 ( luati egali).
Observatie: in cazul miscarii dupa un profil trapezoidal de viteza cazul limita este cel din figura nr.
Fig.nr.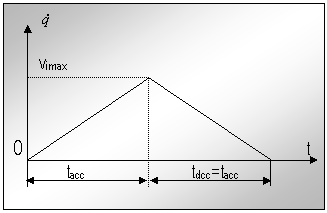
Cazul limita la
miscarea dupa un
profil trapezoidal
de viteza
In acest caz miscarea este numai cu accelerare si decelerare ( lipseste palierul ce indica deplasarea cu viteza constanta). Pentru a se realiza productivitatea maxima trebuie insa, ca si in acest caz, sa se ajunga la viteza maxima.
Tinand cont de cele doua situatii descrise mai sus se alege ca durata a miscarii intre doua puncte tinta:
T= max (26)
adica cel mai lung timp dintre timpii de deplasare calculati la nivelul fiecarei cuple cinematice conducatoare.
Acest mod de alegere este necesar pentru a asigura executia completa a miscarilor la nivelul fiecarei axe mecanice . Adica, se renunta la deplasarea cu viteza maxima a elementelor unora dintre axe, daca altele nu se pot misca decat mai lent.
9.2. Alegerea functiilor conducere.
Se alege cate o functie conducere q(t) pentru elementele fiecarei articulatii. Prorietatile impuse pentru functiile conducere (legi de miscare) sunt :
a) sa fie functii continue si sa aiba cel putin primele doua derivate continue ( functii line);
b) valorile momentane sa se poata calcula prin inlocuirea directa a valorilor pentru t in expresiile lor si sa nu fie necesare iteratii de calcul;
c) valorile momentane calculate sa aiba corespondent fizic bine determinat, adica pozitia, viteza si acceleratia calculate pe baza lor, pentru fiecare valoare a lui t ,sa se poata si executa fizic;
d) sa se evite realizarea de miscari neutile ("hoinare").
In general, aceste conditii sunt indeplinite daca functiile q(t) sunt polinomiale.
9.3. Exemple de functii conducere in coordonate c.c.c
Exemplul 1: Functia conducere polinomiala.
Pentru fiecare axa se alege, ca lege de miscare relativa a elementelor mecanice ( lege de evolutie in timp) o expresie de forma:
![]() (27)
(27)
Cel mai frecvent se utilizeaza polinoamele de gradul 1, 2 sau 3, dar exista si cazul utilizarii unor polinoame de grad superior ( 5, 6 sau 7).
Coeficientii ![]() , i =1,.,6 se determina in etapa de specificare a miscarii
din conditiile impuse trecerii prin anumite puncte tinta sau via.
, i =1,.,6 se determina in etapa de specificare a miscarii
din conditiile impuse trecerii prin anumite puncte tinta sau via.
Exemplul 2: - de utilizare a unei functii polinomiale de ordinul 3 ca functie conducere intre doua puncte via.
Datele problemei:
Se cunosc doua puncte via pentru elementele unei axe( doua pozitii relative
impuse elementelor articulatiei).
Se cunoaste ca miscarea incepe la momentul t = 0 si se termina la t = tf.
Se cunoaste si viteza de trecere prin punctele impuse.
Se cer
Sa se gaseasca coeficientii functiilor polinomiale de gradul 3 care sa asigure
o conducere lina intre cele doua puncte via impuse pentru elementele cuplei cinematice respective.
Rezolvare:
Se alege o functie
polinomiala: ![]() (28)
(28)
![]()
![]()
![]()
![]() Se cunosc:
Se cunosc: 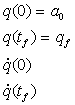 marimi tinta impuse
marimi tinta impuse
Se formeaza sistemul:
![]()
 (29)
(29)
Se rezolva sistemul si se obtin solutiile :
 (30)
(30)
Observatie: Cel mai frecvent acest set de calcule se executa off - line, adica inainte de inceperea desfasurarii miscarii propriu-zise intre cele doua puncte. Acest mod de lucru se poate utiliza daca procesul este bine stabilit de la inceput si nu sufera modificari. Exista si cazuri cand calculul coeficientilor polinomialei trebuie efectuat online ( din mers), daca procesul este extrem de flexibil si desfasurarea etapelor sale depinde de evenimente produse in etapele anterioare.
In figura nr.14 se arata un exemplu de alura pentru o polinomiala de ordinul 3, ca lege de miscare inceputa din repaos si oprita in punctul final (t0=tf=0).
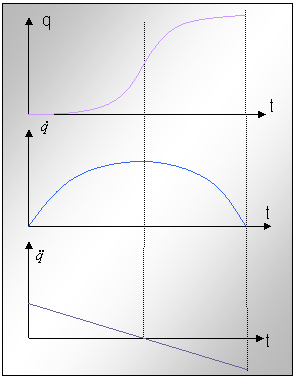
Fig.nr.1 Exemplu de alura pentru o polinomiala deordinul 3
Exemplul 3: Functia conducere cu profil trapezoidal de viteze.
Este cazul cel mai frecvent utilizat in conducerea unui robot in coordonate c.c.c. Este cazul particular in care functia polinomiala utilizata este de ordinul 2. Pentru acest caz alura curbelor aferente pozitiei, vitezei si acceleratiei sunt ca cele reprezentate in figura nr.15. In acest caz elementele articulatiei evolueaza cu accelerat de la 0 la t1, cu viteza constanta de la t1 la t2 si uniform incetinit de la t2 la tf.
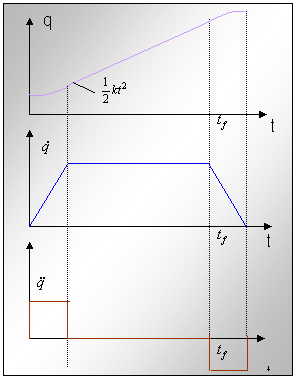
Fig.nr.15. Miscare dupa un profil trpezoidal de viteza
Datele problemei: se cunosc punctul initial si cel final in deplasare si motorul
de actionare al cuplei cinematice conducatoare.
Se cere profilul de viteze dupa care trebuie conduse elementele axei.
Rezolvare: Pornind de la parametrii motorului se pot calcula vitezele si
acceleratiile maxime obtenabile. De regula se doreste pornirea cu viteza si acceleratia maxime si atingerea vitezei maxime posibile ( pentru a se realiza productivitatea maxima). Cu amax si vmax se calculeaza in momentele t1 si t2 in care incepe si, respectiv, se termina portiunea liniara a curbei q(t).
Observatii :
1). In cazul conducerii cu profil trapezoidal de viteza trebuie asigurat cate un interval de timp pentru accelerare si, respectiv, pentru decelerare, in orice situatie. Cazul limita este cel redat in fig. 13.In aceasta situatie acceleratia este mica si nu se mai ajunge la deplasarea cu viteza constanta; miscarea consta dintr-o accelerare pana la viteza maxima si apoi o decelerare de la viteza maxima la 0. In acest caz trebuie insa asigurat ca intervalul 0 - tf sa fie mai mare decat 2tacc, unde tacc este intervalul de timp necesar accelerarii cuplei cu acceleratia data, de la 0 la vmax. tacc este calculabil.
2). In situatia limita din fig.13 , pe graficul q(t) lipseste portiunea liniara. q(t) se compune din numai doua arce de parabola racordate.
3). Cu cat acceleratia este mai mare, cu atat tacc este mai scurt si portiunea liniara e mai lunga. Cu cat acceleratia este mai mica, cu atat tacc e mai lung si portiunea liniara mai scurta.
9.Generarea miscarii in coordonate c.c.c.
Dupa etapa de specificare a miscarii s-au ales timpii de parcurgere si functiile conducere si s-au calculat coeficientii variabilei timp din expresiile functiilor conducere. Aceste date sunt transferate generatorului de traiectorie. Rolul GT este acela de a calcula valorile numerice ale functiilor conducere si derivatele lor la diferite intervale de timp.
Cu o frecventa cuprinsa
intre 20 Hz si 200 Hz ( in functie de viteza de calcul a calculatorului ) se
calculeaza valorile ![]() ,
, ![]() si
si ![]() , parametrii cinematici ai miscarilor ( valori ce trebuiesc
atinse in miscare la diferite momente). Sunt generate astfel puncte ale
traiectoriei descrise de elementele mecanice si vitezele/acceleratiile
aferente.
, parametrii cinematici ai miscarilor ( valori ce trebuiesc
atinse in miscare la diferite momente). Sunt generate astfel puncte ale
traiectoriei descrise de elementele mecanice si vitezele/acceleratiile
aferente.
Aceste valori calculate de GT sunt marimi de prescriere pentru regulatoarele din structura fiecarui sistem de conducere local de la nivelul articular , cu care asigura conducerea nemijlocita a fiecarei axe ( toate sistemele de conducere locale, impreuna, constituie sistemul de actionare al robotului).
Generatorul de traiectorie lucreaza dupa un program care urmareste,in principiu, un algoritm de tipul :
t = t0;
bucla: asteapta dupa noul interval de interpolare
t = t+![]() t ;
t ;
![]()
daca t = tf paraseste bucla ;
daca t![]() tf continua bucla ;
tf continua bucla ;
end.
Observatie : ![]() Principalul calcul pe care-l efectueaza generatorul de
traiectorie in parcurgerea algoritmului este acela al calculului valorilor
momentane pentru functiile conducere si derivatele lor. Rezultatul acestor
calcule reprezinta (in fiecare moment
Principalul calcul pe care-l efectueaza generatorul de
traiectorie in parcurgerea algoritmului este acela al calculului valorilor
momentane pentru functiile conducere si derivatele lor. Rezultatul acestor
calcule reprezinta (in fiecare moment ![]() t) marimile de prescriere pentru regulatoarele din structura
sistemelor de conducere locale de la nivelul cuplelor cinematice conducatoare.
t) marimile de prescriere pentru regulatoarele din structura
sistemelor de conducere locale de la nivelul cuplelor cinematice conducatoare.
Concluzie: GT genereaza puncte prin care trebuie sa treaca elementele fiecarei articulatii intre t0 si tf, specificand si vitezele si acceleratiile aferente. Elementele mecanice descriu si ele cate o traiectorie: arc de cerc, linie dreapta, (dupa tipul cuplelor cinematice - de rotatie sau de translatie).
9.5.Concluzii cu privire la miscarea in coordonate c.c.c.
Acest mod de conducere al unui robot este considerat cel mai simplu si cel mai mic consumator de timp de calcul. Conducerea se efectueaza la nivelul la care si miscarea este produsa ( nivelul articulatiilor). Se porneste de la procesul tehnologic si se determina punctele tinta si via in coordonate operationale ( de multe ori carteziene). Cu analiza cinematica inversa, aplicata o singura data, se determina punctele tinta si via in coordonate c.c.c. ( coordonate articulare, coordonate robot). La nivelul fiecarei axe a robotului se alege ( se specifica) cate o lege de miscare si, in continuare, miscarile sunt urmarite numai la nivel articular.
Folosind functii conducere polinomiale miscarile la nivelul fiecarei axe sunt line, rezultand implicit si o miscare lina pe ansamblul intregului robot (se poate demonstra si matematic).
Desfasurarea miscarii se urmareste numai la nivelul cuplelor cinematice conducatoare, controlerul aferent corectand, pentru fiecare axa, eventualele erori locale. De aici rezulta o acuratete mai scazuta in ceea ce priveste situarile din spatiul operational al robotului.
Observatie : In etapa de generare a miscarii GT, in care s-au
memorat legile de miscare stabilite pentru fiecare axa, incrementeaza variabila
t de la 0 la tf. Pentru fiecare valoare a lui t se calculeaza cate o
valoare ![]() , i =1 - n pentru functiile conducere si derivatele lor.
Aceste valori sunt marimi de prescriere care se transmit controlerului de ax de
la nivelul fiecarei articulatii in parte, spre a fi executate.
, i =1 - n pentru functiile conducere si derivatele lor.
Aceste valori sunt marimi de prescriere care se transmit controlerului de ax de
la nivelul fiecarei articulatii in parte, spre a fi executate.
Desi scopul final urmarit este acela ca punctul caracteristic sa treaca prin toate punctele tinta si via impuse de procesul tehnologic, miscarea nu este condusa si controlata la nivelul punctului caracteristic ( pentru care oricum nu avem traductor), ci la nivelul fiecarei axe unde, de fapt, miscarea este executata.
Intre miscarile elementelor ce constituie o cupla cinematica si elementele celorlalte articulatii nu exista de fapt decat o singura legatura: de regula, incep si se termina simultan.Miscarile tuturor elementelor se desfasoara concomitent, dar sunt si cazuri in care unele elemente se afla in repaos cand altele se deplaseaza.
9.6.Avantajele conduceri unui robot in coordonate c.c.c.
specificarea si generarea traiectoriei se realizeaza direct in variabilele (coordonatele) care sunt reglate la nivelul sistemelor de conducere locale;
coeficientii functiilor conducere se calculeaza simplu;
timpul de calcul pentru generarea miscarilor de prescriere pentru sistemele de conducere locale (valorile momentane ale functiilor q(t) si derivatelor) este redus, foarte aproape de timpul real (adica uneori se pot executa calculele si online);
nu apar situatii in care mecanismul sa devina degemerat.
Nota: Mecanismul devine degenerat
daca pentru o anumita situare a punctului caracteristic in spatiul operational
se obtine,cu analiza cinematica inversa,
pentru cel putin una dintre coordonatele c.c.c valoarea q =![]() . Fiind condus direct in coordonate c.c.c., este evdent ca,
robotului i se prescriu mereu valori reale si finite ale
coordonatelor.
. Fiind condus direct in coordonate c.c.c., este evdent ca,
robotului i se prescriu mereu valori reale si finite ale
coordonatelor.
Observatie: miscarile elementelor mecanice sunt comandate la nivelul fiecarei articilatii separat, in mod independent. In realitate elementele cuplelor cinematice conducatoare nu se pot misca independent , intre ele existand cuplaje (exprimate prin ecuatii neliniare foarte complicate). De efectul acestor cuplaje trebuie tinut cont. In structura sistemelor de conducere locale sunt introduse regulatoarele care se proiecteaza astfel incat sa se tina cont si de aceste cuplaje.
9.7.Dezavantajele conducerii unui robot in coordonate c.c.c.
principalul dezavantaj: miscarea se urmareste la nivelul cuplelor cinematice conducatoare, iar miscarea punctului caracteristic se obtine ca rezultat al miscarilor independente urmarite pe fiecare axa;
nu se urmareste direct miscarea punctului caracteristic, ci pentru elementele ce constituie fiecare cupla cinematica conducatoare se alege cate o functie conducere independenta, iar GT genereaza cate o lege de miscare pentru elementele fiecarei articulatii . Miscarile se executa simultan.
Consecinta: traiectoria punctului caracteristic se obtine ca rezultat al tuturor miscarilor, este greu de exprimat analitic, este greu de anticipat si e o curba greu de urmarit in spatiul vizual uman. De aceea, in acest mod de conducere, operatorul uman trebuie sa garanteze, de la bun inceput, ca desfasurarea etapelor procesului tehnologic are loc astfel incat in nici un moment sa nu survina pericolul de coliziune.
Exemplul clasic de utilizare a acestui mod de conducere este in cazul robotului de sudura in puncte, la care intereseaza numai atingerea tuturor punctelor in care trebuie aplicata sudura (cu o orientare adecvata a efectorului final) si nu intereseaza pe ce traseu se deplaseaza efectorul final intre doua puncte ( iar evitarea coliziunilor trebuie asigurata anticipat). Intereseaza, desigur, si asigurarea deplasarii line.
In cazul conducerii in acest mod, punctului caracteristic i se impune o traiectorie continua in spatiul cartezian. Se alege si se proiecteaza (se calculeaza) legea de miscare a punctului caracteristic pe o traiectorie spatila impusa
de procesul tehnologic. Uneori se determina si vitezele, acceleratiile cu care punctul caracteristic trebuie sa se deplaseze..
Cu analiza cinematica inversa si cu Jacobianul se calculeaza pozitiile, vitezele si acceleratiile de la nivelul cuplelor cinematice conducatoare, iar aceste valori se transmit ca valori prescrise sistemelor de conducere locale care actioneaza fiecare articulatie.
10.1. Generarea miscarii in coordonate carteziene
Si in acest caz generarea punctelor de pe traiectorie se face cu blocul generator de traiectorie.Principial, in cadrul GT generarea punctelor se face ruland un algoritm(program) de tipul :
t=t0;
bucla: asteapta pentru noul interval de interpolare
t=t+![]() t ;
t ;
![]()
![]()
daca t = tf then paraseste bucla;
daca t![]() tf continua bucla;
tf continua bucla;
end.
In acest caz functia conducere se exprima matriceal, H(t) este o matrice cu elemente variabile in timp ce exprima evolutia situarii punctului caracteristic de-a lungul traiectoriei.
La fiecare parcurgere a
algoritmului se calculeaza elementele matricilor ![]() (situare + viteza +
acceleratie) si se efectueaza calculul de conversie din coordonate operationale
(carteziene) in coordonate c.c.c. (articulare).
(situare + viteza +
acceleratie) si se efectueaza calculul de conversie din coordonate operationale
(carteziene) in coordonate c.c.c. (articulare).
Observatie : este necesar un volum de calcule mult mai mare decat in cazul conducerii in coordonate c.c.c. In literatura de specialitate se arata ca volumul de calcule necesar aferent conducerii in coordonate c.c.c. reprezinta 1 - 7 % din volumul de calcule necesar in cazul conducerii in coordonate carteziene.
10.2.Specificarea miscarii in cazul conducerii in
coordonate carteziene
Inainte de a se trece la generarea propriu-zisa a traiectoriei (cu executia unui algoritm de genul celui anterior prezentat) trebuie parcurse doua etape preliminare:
10.2.1. Etapa de determinare a punctelor de definire a traiectoriei carteziene
Aceasta etapa presupune deosebirea a doua situatii diferite :
a) cand se cunoaste expresia analitica a traiectoriei. In acest caz, se calculeaza,
din expresia cunoscuta, diferite puncte care trebuie atinse in diferite momente de timp. Modul de alegere a punctelor poate fi arbitrar sau impus de anumite conside-
rente specifice procesului.
b) cand traiectoria este complicata si exprimarea analitica pe ansamblul ei nu se poate face.De aceasta data, se procedeaza la aproximarea traiectoriei pe portiuni, cu segmente de curbe simple (dreapta, cerc, sinusoida,s.a.),adica se procedeaza la o interpolare pe portiuni a traiectoriei.Apoi se calculeaza, cu expresiile curbelor utilizate la interpolare, diferite puncte de trecere impuse.
10.2.2. Etapa de alegere a functiei ( functiilor) conducere si de calcul
al coeficientilor acestora.
Observatie: cu valorile succesive ale functiei (functiilor) conducere se rea-
lizeaza apoi, GT , generarea traiectoriei.
Etapa a doua se poate realiza in doua moduri diferite:
a) metoda de conducere a unui robot in spatiul cartezian, orientata in spatiul cartezian. (COCM - Cartezian Oriented Cartezian Motion).
Este metoda cea mai mare consumatoare de timp de calcul dintre metodele de conducere a robotilor.Majoritatea calculelor si optimizarilor se efectueaza in spa-
tiul cartezian.
Controlul acuratetei executiei traiectoriei se efectueaza la nivelul punctului ca-
racteristic (reglajele si corectiile se efectueaza in coordonate carteziene).
In acest caz se alege o singura functie conducere, definita matricial, cu care se genereaza succesiv situari prescrise in spatiul cartezian (vezi paragraful 10.3).
Aceste situari sunt convertite apoi, cu analiza cinematica inversa, in puncte prescrise in coordonate articulare si se transmit sistemelor de conducere locala de la nivelul axelor, spre executie.
Erorile de pozitie si orientare se determina intre situarea carteziana impusa si situarea carteziana reala (curenta) a punctului caracteristic. Situarea reala se de-
termina cu analiza cinematica directa utilizand in calcul valorile coordonatelor rela-
tive ale elementelor aferente fiecarei articulatii, citite de la traductoarele amplasate la acest nivel .
Observatie : de regula, trebuie efectuate calcule cu analiza cinematica inversa si analiza cinematica directa de mai multe ori, pentru fiecare punct in parte, pana se ajunge la o eroare acceptabila.
b). Metoda de conducere a robotilor in spatiul cartezian cu orientare in
coordonate c.c.c. (articulare) (JOCM - Joint Oriented Cartezian
Motion
In cazul acestei metode, la specificarea miscarii se calculeaza intai puncte ce definesc traiectoria carteziana impusa/dorita.Din aceste puncte,cu analiza cinemati-
ca inversa, se calculeaza seturi de valori aferente pentru coordonatele c.c.c.
Se alege apoi cate o functie conducere pentru elementele fiecarei articulatii, procedandu-se ca si in cazul conducerii in coordonate c.c.c.( vezi paragraful 9.2).
Cu aceste functii generatorul de traiectorie calculeaza,ulterior, punctele de prescriere pentru miscare.
Functiile conducere sunt, de regula, polinomiale de grad mic. Conducerea se efectueaza urmarind miscarea numai la nivelul cuplelor cinematice conducatoare.
Aceasta metoda se deosebeste,totusi, de cea de conducere in coordonate c.c.c. prin aceea ca sunt luate ca repere obligatorii mult mai multe puncte de pe traiectoria carteziana impusa. Este frecvent utilizata intrucat necesita un volum de calcule mult mai scazut decat COCM.
10.3.Conducerea unui robot in spatiul cartezian cu matricea D(r)
Conducerea unui robot in coordonate carteziene este metoda cu care robotul este condus astfel incat punctul caracteristic sa se deplaseze pe o traiectorie continua impusa in spatiul cartezian. Pentru aceasta se proiecteaza (se calculeaza) legea de miscare a punctului caracteristic pe traiectoria impusa.Uneori se determina si vitezele si acceleratiile cu care se face deplasarea.
Cu analiza cinematica inversa si cu matricea Jacobiana se calculeaza pozitiile, vitezele si acceleratiile aferente pentru elementele articulatiilor, iar aceste valori se transmit ca marimi de prescriere la sistemele de conducere locale.
Pentru a intege complexitatea procedurii se va descrie un exemplu ipotetic.
Se considera trei situari succesive ale unui efector final tip dispozitiv de prehensiune cu doua degete, ca in fig.15.
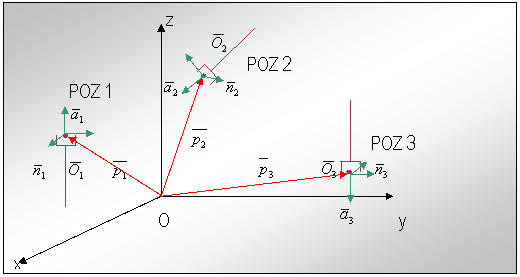
Fig.nr.15.Trei pozitii succesive in spatiu pentru un EF tip DP cu doua degete
Pentru fiecare dintre cele trei puncte din spatiu considerate, se cunoaste situarea sistemului de coordonate atasat EF , adica orientarea axelor - prin versorii n, o si a - si pozitia originii prin vectorul p.Acestea se exprima cu matricile :
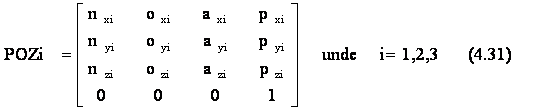
Ne propunem sa descriem trecerea prin cele trei situari date utilizand matricea de conducere D(r) propusa pentru prima data in literatura de R.P.Paul. Pentru simplificare vom considera ca deplasarea intre doua puncte succesive se face dupa o lege de miscare liniara.Cu ajutorul matricii de conducere D(r) propusa de R. P. Paul o situare oarecare k, intre doua situari succesive date, POZn si POZn+1, se poate obtine cu un calcul de forma :
![]()
unde r este o variabila scalara definita cu r = t /T (33) , relatie in care t este timpul curent, iar T este timpul total de deplasare intre POZn si POZn+1.Evident ca
0 ≤ r ≤ 1.
R. P. Paul a propus ca matricea D(r) sa reprezinte trei miscari:
o translatie in coordonate carteziene;
o rotatie in jurul unei axe k care sa asigure alinierea versorului a de la situarea initiala la cea finala;
o rotatie in jurul versorului a care sa asigure orientatarea finala impusa dispozitivului de prehensiune.
![]()
Toate aceste trei miscari se executa
simultan.
Matricea de translatie este de forma:

unde x, y si z sunt valorile totale ale translatiilor necesare pentru a trece de la POZn la POZn+1. Pe masura ce EF este mai aproape de pozitia finala t creste, r creste catre valoarea 1 si deci, conform matricii T(r) , cresc si valorile fractiunilor efectuate din translatiile complete.
Matricea
de rotatie pentru alinierea dispozitivului de prehensiune
este o matrice de rotatie cu un unghi ![]() in jurul unei axe
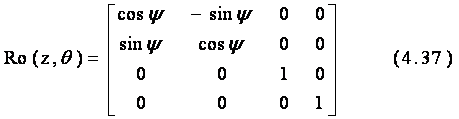
oarecare k, cu expresia :
in jurul unei axe
oarecare k, cu expresia :

(36)
Elementele kx, ky si kz sunt proiectiile
vectorului k pe axele sistemului de
coordonate de referinta;
![]()
![]()
este unghiul de rotatie
in jurul axei k; vers θ =1- cosθ
![]()
In cazul aplicatiei analizate, versorul k se obtine rotind versorul o cu
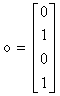
unghiul ψ in jurul
versorului a, a
fiind axa z pentru sistemul de coordonate atasat efectorului final (vezi fig.16).
![]()
Fig.nr. 16 
Rotatia
versorului a
![]() a
a
 n' n
n' n
![]()

![]() o O
o O
![]() ψ
ψ
k
In consecinta vectorul k se obtine cu :
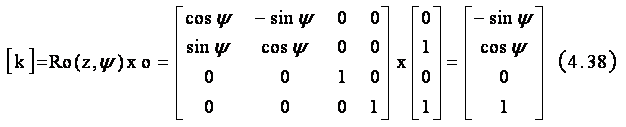
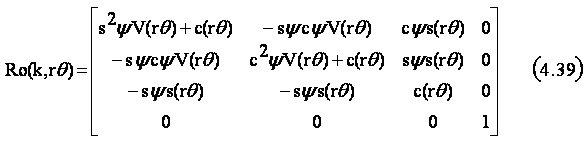
Cu expresia particulara a vectorului k
in jurul caruia trebuie efectuata rotatia de unghi θ, in momentul curent rotatia fiind rθ, putem scrie matricea rotatiei de
aliniere a dispozitivului de prehensiune :
Rotatia de orientare a dispozitivului de prehensiune se face in jurul versorului a, cu un unghi φ si se exprima cu :
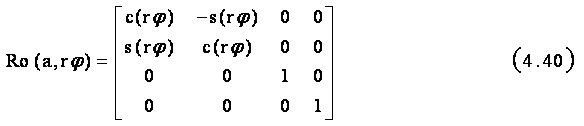
Inmultind cele trei matrici T( r), Ro(k, rθ ) si Ro(a, rφ ) se obtine expresia finala a matricii D(r).

Deoarece pe parcursul miscarii
de la POZ1 la POZ 3 conducerea se va
face folosind mai multe matrici D(r), ce
difera intre ele in functie de segmentul de traiectorie parcurs , se noteaza cu
DI(r) matricea de conducere
care se utilizeaza la deplasarea intre POZ 1 si POZ 2 (prima portiune a
miscarii ), adica:
Problema care se pune
intr-o aplicatie concreta este aceea de a determina valorile concrete pentru x, y, z,![]() si va fi rezolvata in
etapa de specificare a miscarii pornind de la urmatoarele conditii cunoscute :
si va fi rezolvata in
etapa de specificare a miscarii pornind de la urmatoarele conditii cunoscute :
pentru t = 0,
POZ 1 =POZ 1 DI(0) = POZ 1 I, adica DI(0) = I - matricea unitate;
pentru t =T,
POZ 2 =POZ 2 DI(1) , adica DI(1) =POZ 2 POZ 1-1
Din acest sistem se pot calcula
valorile x, y, z, ![]() .Sistemul este rezolvat in literatura de specialitate si are
solutiile (42). In aceste solutii se
utilizeaza elementele, date, ale matricilor POZ1 si POZ 2.
.Sistemul este rezolvat in literatura de specialitate si are
solutiile (42). In aceste solutii se
utilizeaza elementele, date, ale matricilor POZ1 si POZ 2.
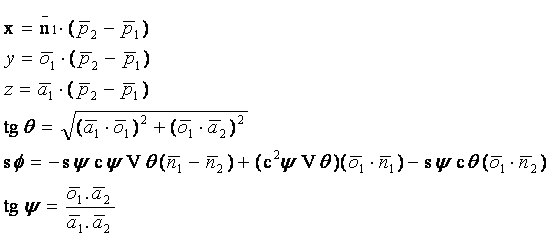
![]()
![]()
![]()
![]()
(42)
Cu valorile (42) calculate si inlocuite in expresia matricii D(r), singurul parametru variabil care se va incrementa este r. Incrementand r, se obtin valorile numerice succesive concrete pentru matricile DI(r). Cu acestea se calculeaza situarile succesive, efectuand inmultiri matriciale de tipul :
POZ k= POZ1 DI(r). (41)
Cu analiza cinematica inversa, din situarile POZ k se afla coordonatele articulare, iar acestea se transmit ca marimi de prescriere la sistemele de conducere locale cu care sunt puse in miscare elementele mecanice.
Se realizeaza astfel deplasarea dupa o lege de miscare liniara intre POZ1 si POZ 2, utilizand matricea de conducere DI(r) . Folosind aceeasi matrice DI(r) s-ar putea utiliza aceeasi lege de miscare liniara si pentru deplasarea intre POZ 2 si POZ 3. Panta graficului miscarii dintre POZ1 si POZ 2 difera insa de cea a celeia dintre POZ 2 si POZ 3.Astfel, in POZ 2 s-ar produce un soc, ceea ce trebuie evitat. Schimbarea pantei legii de miscare are loc din cauze spatiale : translatiile si rotatiile totale ce trebuie efectuate sunt diferite pe cele doua portiuni, iar timpul de deplasare se doreste a fi mentinut tot T. Este vorba, de fapt, de o schimbare a vitezelor de parcurs pe cele doua segmente ale miscarii.
Pentru a se asigura o deplasare lina nu numai intre POZ1
si POZ 2 si intre POZ 2 si POZ 3, ci si
la trecerea prin pozitia POZ 2, se pune problema realizarii unui racord intre graficele
ce reprezinta legile de miscare ale parametrilor rx, ry, rz, r![]() , r
, r![]() , r
, r![]() . In majoritatea aplicatiilor concrete unghiul ψ se mentine acelasi pe ambele
segmente ale deplasarii si nu este considerat ca variabila a miscarii.
. In majoritatea aplicatiilor concrete unghiul ψ se mentine acelasi pe ambele
segmente ale deplasarii si nu este considerat ca variabila a miscarii.
Pentru rezolvarea racordului necesar, se reprezinta grafic legile de miscare pentru cei cinci parametrii rx,ry,rz,rθ, rφ in concordanta cu cele trei situari date (fig.nr.17).
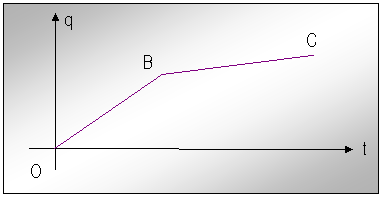
Fig.nr. 17
Graficul de
variatie in timp
a coordonatei
generalizate
In fig.17 : q este coordonata generalizata rx, ry, rz, rθ, rφ
O este momentul trecerii EF prin POZ1;
B este momentul trecerii EF prin POZ 2;
C este momentul trecerii EF prin POZ 3.
Asa cum se observa si din graficele din fig.17. in punctul B, corespunzator situarii POZ 2 pentru EF, are loc o schimbare de panta ce va produce un soc la trecerea acestuia prin POZ 2.
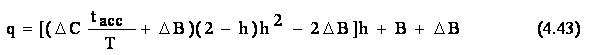
Evitarea socului se face alegand, intre cele doua portiuni cu evolutie
liniara, o lege de miscare de racord, care are o expresie polinomiala
de forma :

unde cu h s-a procedat la o schimbare de variabila, calculata cu :
si utilizand t - timpul curent, respectiv tacc - durata accelerarii.
In vederea simplificarii calculelor si obtinerii unei expresii mai simple pentru curba de racord, teoretic, se procedeaza la o schimbare de origine pentru variabilele q ca in fig.18 :
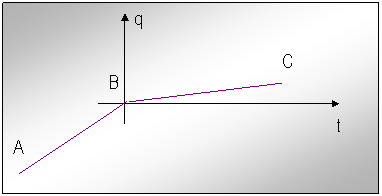
Fig.nr.18 Schimbare de origine pentru variabilele q
Cu aceasta schimbare de origine valoarea lui B din ecuatiile (43) devine zero.
Momentul inceperii miscarii accelerate, efectuata pentru trecerea de la o viteza la alta, poate fi ales, in principiu, arbitrar.Se obisnuieste,insa, sa se aleaga momentul inceperii accelerarii la r = 0,9, adica t = 0,9 T, in raport cu momentul plecarii din POZ1. Acestui moment ii corespunde, in cartezian, un punct POZ1' care se calculeaza cu:
POZ 1'=POZ 1 DI(0,9) (45)
Lui POZ1' pe graficele q ii corespund punctele A' de pe graficele din fig.19. Punctele B' sunt cele din momentul in care miscarea accelerata s-a incheiat. Marimile ΔB si ΔC din ecuatiile (43) sunt si ele reprezentate pe graficele din fig.19.
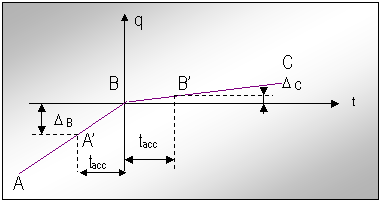
Fig.19. Reprezentarea intervalului de timp in care are loc modificarea vitezelor
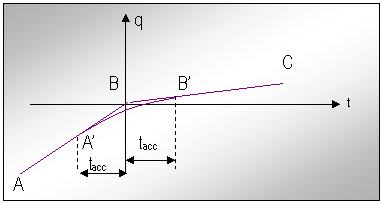
Fig.nr.20. Racordarea graficelor legilor de miscare
Pentru a calcula expresia polinomiala ce reprezinta legea de racord trebuie calculate valorile ΔB si ΔC. Datorita schimbarii de origine, se poate scrie ca :

Deci diferentele ![]() C din polinomoalele q(h) (43) sunt cunoscute.
C din polinomoalele q(h) (43) sunt cunoscute.
Dar aceste valori reprezinta chiar translatiile totale si rotatiile totale ce trebuie efectuate in miscarea de la B la C, echivalenta deplasarii efectorului final de la POZ2 la POZ 3. In consecinta, cu solutiile de mai sus se calculeaza elementele unei a doua matrici, DII(r), cu care se efectueaza conducerea intre situarile POZ 2 si POZ3.
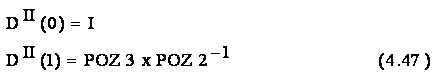
![]()
Deci:
Pentru a determina
diferentele ![]() B din expresia polinomialelor q(h) (43) se imagineaza o
miscare fictiva, in sens invers, de la B la A' pentru fiecare dintre
coordonatele q. O astfel de deplasare ar corespunde miscarii efectorului final de la POZ 2 la POZ 1' cu POZ 1'=POZ1 DI(0,9).
B din expresia polinomialelor q(h) (43) se imagineaza o
miscare fictiva, in sens invers, de la B la A' pentru fiecare dintre
coordonatele q. O astfel de deplasare ar corespunde miscarii efectorului final de la POZ 2 la POZ 1' cu POZ 1'=POZ1 DI(0,9).
Daca s-ar conduce o astfel de miscare s-ar folosi o a treia matrice de conducere DIII(r), pe portiunea de traiectorie POZ 2, POZ 1'.Se presupune ca aceasta miscare s-ar efectua tot in timpul T.
![]()
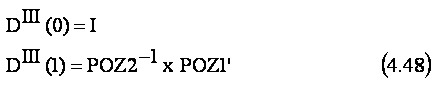
Matricea DIII(r) nu se va folosi,evident, la conducerea
propriu-zisa ci se va folosi doar ca etapa intermediara de calcul. Valorile ![]() B sunt usor de gasit din elementele matricii DIII(1) .
B sunt usor de gasit din elementele matricii DIII(1) .
Cu acestea, sunt cunoscute toate elementele necesare realizarii racordului dintre A' si B' pe perioada t = [ -tacc,tacc ], adica se stiu expresiile polinoamelor q(h) (43).
In acest fel, se cunosc legile de variatie pentru coordonatele generalizate si se poate scrie o noua matrice DIV(r) care se foloseste in conducerea efectorului final pentru efectuarea racordului.
![]()
Datorita efectuarii racordurilor pentru coordonatele q, nici una dintre coordonate nu trece exact prin punctul B si deci nici efectorul final nu va trece exact prin POZ 2, care devine astfel un punct pseudovia in coordonate carteziene.
In momentul in care coordonatele q trec prin punctele B' racordarea s-a incheiat, urmand sa se faca deplasarea pe cel de-al doilea segment de dreapta.
Pentru ca la efectuarea racordului s-a ales ca originea miscarii sa fie punctul cartezian POZ1', pentru simplificarea operatiilor se va alege ca punct
de inceput si pentru miscarea pe cel de-al doilea segment al traiectoriei carteziene tot POZ1' (A' de pe graficele coordonatelor q ).
Pentru calculul situarilor corespunzatoare trecerii coordonatelor q din B' pana in C, se foloseste o noua matrice, notata DV(r), in care pentru variabile se aleg legi de variatie de forma :
q =B+![]() C h
C h
h=t/T, (50)
t![]() [tacc,T ].
[tacc,T ].
![]()
In acest fel se executa si ultimul segment al traiectoriei carteziene :
In cele prezentate mai sus s-a presupus ca unghiul ψ se mentine acelasi pe ambele segmente liniare ale deplasarii.Daca, insa, ψ nu poate fi acelasi pe ambele segmente, in timpul racordarii celor doua miscari liniare trebuie schimbata si valoarea sa. Presupunand ca pe primul segment acest unghi este ψA , iar pe segmentul al doilea trebuie sa fie ψC , trecerea de la o valoare la alta se face dupa o lege de variatie liniara de forma :
( h ) = (ψC - ψA) . h + ψA
unde h este variabila (44) aleasa si pentru racord. Se asigura,astfel, si modificarea fara soc a directiei axei k folosita ca axa a rotatei de aliniere.
In acest paragraf s-a aratat cum se calculeaza sirul de situari aflate intre POZ1 si POZ 3 in spatiul cartezian. Miscarile se executa, insa, la nivelul cuplelor cinematice conducatoare si, de aceea, pentru fiecare situare carteziana intermediara POZk se efectueaza cate un calcul cu analiza cinematica inversa si se gasesc coordonatele articulare aferente. Aceste coordonate se transmit ca marimi de prescriere la sistemele de conducere locale care conduc, pana la urma, elementele mecanice.
10. Metoda de conducere a unui robot in spatiul cartezian,
cu orientare in spatiul cartezian
(COCM - Cartezian Oriented Cartezian Motion)
Este metoda cea mai mare consumatoare de timp de calcul dintre toate meto-
dele de conducere a robotilor. Din cauza volumului mare de calcule legile de miscare realizabile se compun numai din segmente de dreapta racordate intre ele.
Controlul acuratetei executiei miscarii se efectueaza la nivelul punctului cara-
cteristic. Reglajele trebuie sa corecteze erorile situarilor spatiale ale efectorului final.
Se foloseste o singura functie conducere exprimata matriceal cu care se ge-nereaza succesiv situarile efectorului final din cartezian. Aceste situari sunt converti-
te in puncte de prescriere in coordonate c.c.c. si se transmit sistemului de actionare spre executie.
Astfel, din pozitia carteziana impusa, cu analiza cinematica inversa se deter-
mina coordonatele articulare impuse.Cu sistemele de conducere locale se comanda
miscarile elementelor cuplelor cinematice conducatoare spre valorile prescrise.Dupa efectuarea miscarilor, traductoarele, amplasate la nivelul c.c.c.,transmit pozitiile arti-
culare reale.Cu analiza cinematica directa se calculeaza situarea reala obtinuta pen-
tru efectorul final si, apoi, se calculeaza eroarea carteziana.Din aceasta, cu analiza cinematica inversa se calculeaza erorile aferente fiecarei axe.Cu sistemele de con-
ducere locale se comanda corectia erorilor articulare.Cu traductoarele de la nivelul axelor se masoara noile pozitii reale. Cu analiza cinematica directa se determina situarea carteziana reala de la nivelul efectorului final s.a.m.d.
Practica a dovedit ca este suficienta parcurgerea de cate trei ori a sirului de calcule analiza cinematica inversa-reglare-analiza cinematica directa pentru a corec-
ta, cu suficienta precizie, o situare carteziana impusa.Cu toate acestea,volumul de calcule este foarte mare si extrem de dificil de efectuat in timp real.
Avantajul metodei consta in aceea ca, in cazul utilizarii ei, traiectoria descrisa este un concept direct bine reprezentat in spatiul vizual uman,fiind deci usor de ur-
marit de catre operatorul uman.
Acuratetea in realizarea unei traiectorii carteziene impuse este foarte buna, deoarece corectiile se realizeaza la nivelul situarii efectorului final (a punctului ca-
racteristic).
Metoda prezinta insa urmatoarele dezavantaje:
functia conducere (matriceala) se calculeaza mai greu;
calculul valorilor momentane ale acesteia presupune calculul valorilor tuturor elementelor unei matrici;
necesita transformari de coordonate (cartezian → c.c.c. si c.c.c.→ cartezian) pentru fiecare punct. In timp real aceste calcule se efectueaza greu.
traductoarele de pozitie/orientare sunt amplasate la nivelul articulatiilor.Traduc-
toarele carteziene de precizie sunt mult prea costisitoare spre a se putea utiliza.
Alte dezavantaje sunt cauzate de faptul ca transformarea de coordonate cartezian → c.c.c. nu este biunivoca:
exista situatii cand o anumita situare a punctului caracteristic se poate realiza prin mai multe configuratii ale bratului, adica exista asa numitele nesingularitati ale mecanismului;
pentru o anumita situare a punctului caracteristic, efectuand analiza cinematica inversa, pot rezulta pentru anumite coordonate articulare valori infinite si, astfel, mecanismul devine degenerat sau situarea impusa este nerealizabila din punct de vedere fizic. In aceste cazuri se procedeaza la aproximari,pentru coordonatele articulare folosindu-se valori apropiate de cele rezultate din calcul, dar finite si/sau realizabile fizic.
In cazul in care se tine cont si de dinamica, calculele sunt si mai complicate.
Limitarile de forte/cupluri,vitezele si acceleratiile realizabile sunt cunoscute pentru
fiecare motor care actioneaza elementele cate unei cuple cinematice conducatoare.
Acestea trebuie corelate cu constrangerile impuse de urmarirea traiectoriei cartezie-ne.
cu orientare in c.c.c.
( JOCM - Joint Oriented Cartezian Motion)
In acest caz, la specificarea miscarii se calculeaza intai puncte de definire ale traiectoriei carteziene impuse. Din aceste puncte, cu analiza cinemtica inversa, se calculeaza seturi de coordonate articulare aferente. Apoi, se alege cate o functie conducere la nivelul fiecarei cuple cinematice conducatoare si se procedeaza la ge-
nerarea traiectoriei la nivel articular.
Functiile conducere sunt (de obicei) polinomiale de grad mic.Conducerea se efectueaza urmarind miscarea numai la nivelul axelor.Reglajul se asigura numai cu verificarea acuratetei miscarilor elementelor cuplelor cinematice conducatoare.
Aceasta metoda este cel mai frecvent utilizata pentru ca necesita un volum de calcule mult mai scazut.
Principalul dezavantaj al metodei este ca se pierde din acuratetea urmaririi traiectoriei carteziene impuse. Au fost ,insa, puse la punct metode rapide, cu calcule iterative, prin care se face corectia erorilor carteziene.
Observatie: aceasta metoda se aseamana cu metoda de conducere in coor-
donate c.c.c. Deosebirea consta in aceea ca, fata de conducerea in coordonate arti- culare se folosesc mult mai multe puncte exacte de pe traiectoria carteziana, caro-
ra li se aplica analiza cinematica directa.
Esenta conducerii unui robot consta in prescrierea miscarii si punerea in miscare a sistemului mecanic.
Orice sistem mecanic are una sau mai multe frecvente de rezonanta.
Conducerea unui robot se realizeaza cu mijloace numerice (digitale). La co-
manda numerica, comenzile catre sistemul mecanic se aplica in momente discrete (distincte) , cu toate ca se folosesc functii line in conducere.
Observatie: sugestiv, se poate asemui modul de aplicare al comenzilor catre sistemul mecanic cu ritmul de functionare sacadat al unei masini de cusut.
La aplicarea unei comenzi de trecere de la un punct la altul, in momentul aplicarii comenzii apare un anumit soc. Socul este mai mare sau mai mic in functie de metoda de conducere utilizata.
![]()
Daca
frecventa de comanda de trecere de la o situare impusa la alta se alege astfel
incat :
se produce excitarea pe una dintre frecventele de rezonanta frez ale sistemului mecanic si intrarea in oscilatie a acestuia.
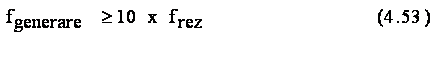
Pentru a evita excitarea
pe frez a sistemului mecanic este necesar ca generarea comenzilor de
trecere de la un punct la altul sa se
faca cu o frecventa:

sau
Din relatia (54) rezulta ca ideal ar fi ca, in conducere, toate calculele afe-
rente gasirii unui nou punct de prescriere sa fie efectuate intr-un timp mai scurt decat Trez/10.
In cazurile cele mai rapide Trez= 8.10 ms, adica Trez/10 = 0,8.1 ms. Un astfel de interval de timp necesar pentru efectuarea tuturor calculelor aferente con-
ducerii unui robot la un nou punct de prescriere este o restrictie severa. Problema apare cu mai mare acuitate in cazul conducerii in coordonate carteziene cu orientare in coordonate carteziene.
O astfel de restrictie impusa duratei de efectuare a calculelor (≤ 1 ms, calcule in timp real ) este severa pentru orice tip de calculator .
11.1.Procedura de efectuare a calculelor
In comanda numerica, ca procedeu general, se foloseste discretizarea :
intreaga durata a procesului de conducere se imparte in intervale egale si cat mai scurte de timp. Un astfel de interval a fost numit in automatica perioada de discre-
tizare, fiind notata uzual cu T. In alte discipline tehnice se foloseste si denumirea
perioada de esantionare (fig.21).
Principial, pe durata fiecarei perioade de discretizare, trebuie sa se efectueze toate calculele aferente conducerii, pentru cate un pas al miscarii. Din considerente-
le aratate anterior trebuie sa se aleaga : T ≤Trez/10.
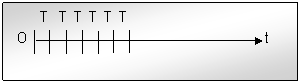
Fig.nr.21. Impartirea in perioade de dicretizare
In actionarile moderne, un sistem de actionare comandat numeric este considerat rapid daca opereaza cu o peroada de discretizare de T = 0,8.1 ms. Sistemul de actionare asigura insa numai conducerea nemijlocita a elementelor cu-
plelor cinematice conducatoare. Evident deci ca, in acest interval de timp, nu se pot efectua toate calculele aferente conducerii robotului la un nou punct de prescriere.
Trebuie efectuate toate calculele pentru specificarea,generarea si conducerea nemij-
locita a miscarii.
Aceasta aparenta imposibilitate, de se a efectua pe durata unui interval de timp T toate calculele, se evita adoptand ca procedeu general solutia de a se exe-
cuta in T=0,8.1 ms numai calculele aferente conducerii nemijlocite in (calculele
din sistemele de conducere locale).
Pentru celelalte calcule se procedeaza in urmatoarele moduri:
I. in cazul in care procesul tehnologic se cunoaste apriori cu exactitate, calculele se efectueaza off-line
a).in cazul conducerii in coordonate carteziene.
Programatorul (operatorul uman) cunoaste cu exactitate procesul tehnologic si impune punctului caracteristic o traiectorie optimala, realizand off-line programul de conducere pe traiectorie carteziana (calculand D(r),paragraful 10.3). Se incrementeaza (off-line) variabila t, respectiv r, si cu valorile succesive ale acestora se calculeaza sirul de matrici D(r) aferente.Cu matricile D(r) astfel calculate se gaseste secventa de situari POZ k pe care trebuie sa le ocupe punctul caracteristic in fiecare t.
Pentru fiecare situare carteziana calculata se aplica analiza cinematica inver-
sa si se gasesc coordonatele articulare qij, i=1.6 aferente. In final, se memoreaza
coordonatele articulare aflate prin calcul,iar la momentul executiei miscarii se preiau
aceste valori din memorie.
b). in cazul conducerii in coordonate c.c.c.
Procesul tehnologic impune trecerea prin anumite puncte carteziene. Cu ana-
liza cinematica inversa se calculeaza,din punctele impuse, coordonatele c.c.c. afere-
nte. Pentru fiecare cupla cinematica conducatoare se alege apoi cate o functie ( poli-
nomiala) si se calculeaza coeficientii acestor functii, pornind de la valorile rezultate din punctele impuse de proces.
Calculul sirului de puncte concrete de tecere pe parcursul miscarii este efec-
tuat de generatorul de traiectorie, pe baza functiilor conducere alese, si se poate face,in multe cazuri, si on-line.
Observatie: metoda b) se poate aplica si in cazul conducerii in coordonate carteziene cu orientare in coordonate c.c.c.
Metoda I. se poate aplica numai daca procesul tehnologic este foarte bine cunoscut si nu apar situati necunoscute, neprevazute si/sau ramificatii de tipul : daca,., atunci,.,altfel, iar situarile obiectelor din spatiul de lucru al robotului sunt riguros respectate (disciplina tehnologica).
II. in cazul unor procese tehnologice complexe sau
incomplet cunoscute apriori.
Modul de desfasurare a unora dintre etapele procesului tehnologic pot depinde de evenimente petrecute pe parcursul derularii sale. Disciplina tehnologica este deseori incalcata, pot sa apara obstacole, situatii neprevazute, etc. In astfel de cazuri, situarile succesive ale punctului caracteristic nu pot fi calculate off-line, ci trebuie calculate on-line.
Intrucat calculele pentru cate un punct exact al traiectoriei nu se pot efec-
tua la fiecare T, se adopta solutia de a calcula cate un punct (exact) numai la fieca-
re N perioade de esantionare ( tipic N = 25.30 ). Calculele pentru urmatorul punct prescris pentru miscari se efectueaza in avans cu cativa pasi (1-2 etape de proces, daca e posibil).
Pentru conducerea nemijlocita (conducerea cu controlerul de ax,vezi fig.2.1) trebuie,insa, respectata strict durata perioadei T = 0,8.1 ms. Asta inseamna ca la fiecare T trebuie sa apara, pentru fiecare sistem de conducere local, cate o marime de prescriere. Puncte de prescriere exacte sunt insa calculate numai la fiecare N .T !
In aceste situatii se foloseste o metoda cu care, intre doua puncte de prescri-
ere exacte (calculate la intervale N.T), se calculeaza puncte de prescriere suplimen-
tare cu un procedeu de interpolare liniara (vezi paragraful 11.2), prin care volumul de calcule este mult redus.
III. in cazul in care se efectueaza si calcule de dinamica
Timpul necesar efectuarii calculelor pentru determinarea unui nou punct al deplasarii este extrem de lung. In astfel de situatii se procedeaza la oprirea robotului intr-un punct cartezian (intr-o situare) si se asteapta terminarea calculelor aferente punctului urmator.
11.2.Interpolarea liniara.
Fie doua puncte , din spatiul cartezian, F0 si F1, calculate exact intr-un inter-
val de timp N.T de catre generatorul de traiectorie. Cu analiza cinematica inversa se calculeaza q0i si q1i, i=1.6, seturile de valori in coordonate c.c.c. (articulare), aferen-
te punctelor considerate.
Intre punctele de prescriere exacte calculate in coordonate c.c.c. se mai calculeaza, pentru fiecare axa, puncte de prescriere intermediare pseudoexacte, folosind relatia:
qi( t )=q1i - ( T1-t ).(q1i-q0i )/ T1 (55)
unde:
qi (t ) - legea de variatie in timp a valorilor coordonatei articulare i;
q1i, q0i - puncte de prescriere exacte;
T1 - intervalul de timp necesar deplasarii intre cele doua puncte;
t - timpul curent.
i = 1 6, pentru cazul unui robot uzual cu 6 axe.
Relatia qi(t ) (55) este liniara in timp, adica intre doua puncte de prescriere exacte se asigura o miscare cu viteza constanta pe fiecare axa.
Calculul este efectuat de un bloc dedicat numit interpolator (vezi cap.II, fig.
2.1).El poate fi un bloc software sau un microcalculator.Prin introducerea acestuia se
genereaza, catre sistemele de conducere locala de la nivelul axelor robotului,cate un
punct de prescriere, exact sau pseudoexact, la fiecare T.
Observatii
1).Pentru regulatoarele care executa conducerea nemijlocita a axelor, trebuie gene-
rat cate un punct de prescriere la fiecare T. Folosind interpolarea liniara, majoritatea
dintre acestea sunt pseudoexacte, dar la fiecare N.T se transmite si cate un punct exact;
2).Interpolatorul poate fi inclus fie in generatorul de traiectorie,fie in controlerul de ax
( fig.2.1);
3). Folosind puncte de prescriere pseudoexacte desigur ca acuratetea trecerii prin punctele carteziene impuse poate fi afectata. Exista, insa, procedee de determinare (prin calcul) a numarului minim de puncte de prescriere exacte ce trebuie cunoscute si utilizate in conducere, pentru ca intre ele sa se poata proceda la interpolarea lini-
ara si acuratetea deplasarii in spatiul cartezian sa se mentina in limite admise.
11.3.Algoritmul de determinare al numarului minim de puncte exacte
de pe o traiectorie spatiala, cu care se asigura o deviere limitata
In cazul utilizarii interpolarii liniare, folosindu-se puncte de prescriere pseudoexacte, poate sa rezulte o deviere inacceptabila de la traiectoria spatiala impusa.Situatia se poate reprezenta ca in fig.nr.
( desen cu traiectorie si puncte pe langa ea)
Fig. nr. 22. Puncte din spatiul cartezian situate in afara traiectoriei impuse
In fig. 22 F0 si F1 sunt doua puncte exacte de pe traiectoria carteziana impusa.
Acestea sunt calculate la intevale de timp N Te . Intre cele doua puncte exacte,
situate pe traiectorie, la fiecare Te se calculeaza puncte de prescriere intermediare , folosind interpolarea liniara (cu care se asigura o deplasare cu viteza constanta). Se obtin ,astfel, prin calcul,puncte in spatiu pseudoexacte, notate cu x pe fig.22 .
Punctele intermediare calculate nu se situeaza in mod obligatoriu pe traiectoria carteziana impusa,fiindca ele nu au fost calculate cu matricea D(r).
Intre punctele intermediare elementele mecanice efectueaza miscarile simul-
tan si cu viteza constanta.Intre miscarile efectuate pe axe diferite nu exista o legatu-
ra anume impusa.
Daca se efecteaza analiza cinematica directa,nu exista nici un motiv ca din calcul sa rezulte puncte exacte de pe traiectoria carteziana. Folosind interpo-
larea liniara se procedeaza de fapt la conducerea in spatiul cartezian cu interpolare in coordonate articulare.
F0 si F1 sunt insa suficient de apropiate pe traiectorie, fiindca intervalele de timp N Te sunt relativ scurte.In plus, valorile de timp cu care se incrementeaza variabila t din relatia (55) sunt mici.In consecinta,abaterile x de la traiectorie nu sunt mari.Exista insa cazuri cand nu se admit nici macar aceste mici abateri.
a.Calculul numarului minim de puncte exacte pentru a asigura o
abatere limitata de la traiectoria carteziana impusa,cand se aplica
interpolarea liniara
Pentru a se asigura incadrarea abaterii de la o traiectorie carteziana impusa in limitele admise de particularitatea unei anume aplicatii, se utilizeaza un algoritm
de corectie ce permite determinarea numarului minim de puncte exacte de pe traiectorie care trebuie utilizate.
Fie F0 si F1 doua puncte exacte de pe traiectoria spatiala (calculate cu D(r)).
Cu analiza cinematica inversa se afla seturile de valori aferente pentru coordonatele articulare q0i si q1j , i,j = 1-k, k fiind numarul de axe ale robotului.Intre aceste puncte exacte, folosind relatia (55) se calculeaza si puncte de prescriere suplimentare qs(t).
Se calculeaza,pe de o parte, un set de coordonate c.c.c. qi(t*) ,i= 1-k, folosind relata de interpolare (55).Acestea sunt coordonatele de prescriere folosite pentru a
comanda robotul intr-un moment arbitrar t*.Cu analiza cinematica directa se afla punctul cartezian aferent Fi( t*) , situarea la care ar ajunge punctul caracteristic al robotului, daca deplasarea ar fi codusa folosind interpolarea liniara.
Apoi, cu relatiile memorate in Generatorul de Traiectorie pentru calculul valorilor curente ale elementelor matricii de conducere D(r),se calculeaza punctul
punctul exact Fd (t *) in care ar trebui sa ajunga punctul caracteristic (PC) in momentul t*.
Situarea PC in cele doua puncte Fi (t*) si Fd (t*) se exprima cu matricile :
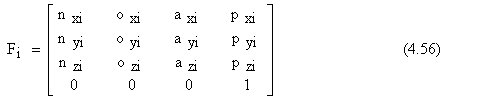
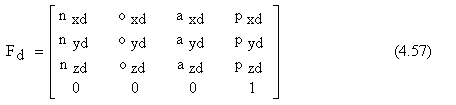
Evident ca cele doua puncte nu sunt coincidente.Intre ele exista atat o abatere de pozitie cat si una de orientare.
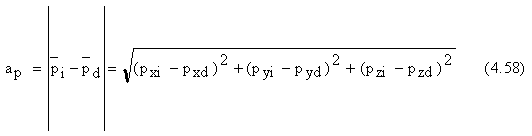
Abaterea de pozitie se calculeaza cu o relatie simpla:
In orientare eroarea se exprima prin faptul ca sitemul de coordonate atasat PC trebuie rotit in asa fel incat orientarea sa sa ajunga de la cea aferenta Fi la cea aferenta Fd :
Ri x Rot(n,Φ) = Rd ( 59)
In relatia (59) Rot(n,Φ) este o matrice de rotatie in jurul axei n cu unghiul Φ , n fiind axa in jurul careia trebuie rotit SC atasat PC ,iar Φ unghiul rotatiei ce trebuie efectuata pentru trecerea de la Fi la Fd .Din relatia (59) :
Rot(n,Φ ) = Ri -1 x Rd (60)
adica diferenta de orientare intre situarile din cele doua puncte carteziene se determina inmultind inversa submatricei de rotatie initiala cu submatricea finala.
Asadar, diferenta intre cele doua puncte (cel exact si cel obtinut prin interpolare) se determina calculand :
a) abaterea (eroarea) de pozitie,utilizand relatia (58) ;
b) matricea de rotatie Rot (n,Φ ) .
Cu acestea se determina diferenta dintre cele doua puncte,adica se verifica daca punctul Fi ( t* ) este suficient de apropiat de punctul Fd ( t* ) de pe traiectoria carteziana.
Masura noncoincidentei se exprima cu eroarea de pozitie ap si unghiul δrot (cel din matricea Rot (n,Φ )).
In general,in aplicatii , se impune ca ap ≤ apmax si δrot ≤ δrotmax ,adica se impune:
o deviere pozitionala maxima de la traiectoria carteziana;
o deviere maxima a orientarii in raport cu cea corespunzatoare unui punct exact de pe traiectorie.
Verificarea abaterilor trebuie efectuata des si trebuie facute permanent corectii.
b. Algoritmul propriu-zis
In cazul conducerii unui robot pe traiectorie carteziana continua folosind interpolarea liniara, se poate folosi algoritmul prezentat in cele de mai jos, cu care se asigura o deviere limtata de la respectiva traiectorie impusa.
Observatie:in limba engleza pentru "deviere limitata" se utilizeaza expresia bounded deviation.
Algoritmul isi propune sa afle numarul minim de puncte exacte de pe traiecto-
rie care trebuie utilizate, astfel ca, desi se foloseste interpolarea liniara,sa nu se de-
paseasca erorile admise/ impuse.
In rezumat, algoritmul cu care se asigura o deviere limitata de la traiectoria carteziana impusa este dupa cum urmeaza :
Fie F0 si F1 doua puncte carteziene exacte - calculate cu D(r).
S1 : Se aplica analiza cinematica inversa si se afla, aferent ambelor puncte carte-
ziene, setul de coordonate articulare q0i si q1i, i =1-k, k fiind numarul de axe ale robotului.
S2 : Pentru fiecare articulatie se calculeaza cate un punct de mijloc :
![]()
S2' : Se aplica analiza cinematica directa si se calculeaza punctul cartezian Fm care corespunde punctelor qim , i = 1-k, de la nivel articular.
S3 : Se calculeaza punctul cartezian de mijloc Fc situat itre F0 si F1
![]()
![]()
![]()
S4 : Se verifica daca Fm si Fc coincid sau difera intre ele.Cu alte cuvinte,se calcu-
leaza :

si se verifica daca aP ≤ apmax si daca δrot ≤ δrot max , adica se verifica daca eroarea se incadreaza in limitele acceptate. Daca eroarea este mai mica decat cea maxim admisa, atunci este suficient sa se foloseasca numai cele doua puncte exacte F0 si F1, iar intre ele se poate folosi in conducere interpolarea liniara fara riscul de a se depasi devierea admisa de la traiectoria carteziana impusa.
Daca aP ≥ apmax sau daca δrot ≥δrot max, nu este suficienta utilizarea numai a celor doua puncte exacte F0 si F1 pentru a se putea folosi in conducere interpolarea liniara,ci mai trebuie adaugate si alte puncte exacte de pe traiectorie. Unul dintre acestea este chiar Fc. In continuare se considera perechile de puncte F0 cu Fc respectiv Fc cu F1 si se mai efectueaza odata calculele conform algoritmului descris s.a.m.d.
Pasii S1-S4, mai sus prezentati, se repeta de atatea ori pana cand eroarea ajunge sa se incadreze in limitele admise.
Observatie : Volumul de calcule implicat de parcurgerea algoritmului este suficient de mare si se efectueaza off-line, cu cativa pasi in avans fata de momentul in care robotul trebuie condus la punctele stabilite cu algoritmul.
S-a dovedit practic ca sunt suficiente doua parcurgeri ale algoritmului pentru a afla numarul de puncte exacte necesare in conducerea pe traiectoria carteziana impusa, astfel ca interpolarea liniara sa poata fi utilizata in calcule fara sa provoace o deviere nepermisa de la traiectoria exacta.
12. Problema interpolarii.
La incheierea capitolului dedicat metodelor de conducere a robotilor,trebuie facuta o mentiune cu privire la modul in care se intelege notiunea de interpolare.In cel mai complex caz, cel al conducerii unui robot in coordonate carteziene pe traiec-
torie impusa, se poate ajunge la a se folosi patru niveluri de interpolare :
1). Aproximarea traiectoriei carteziene,pe portiuni, cu segmente de curbe simple (drepte, arce de cerc, arce de parabola, hiperbola si sisusoida);
2). Daca in urma calculelor cu analiza cinematica inversa, pentru unele puncte/situ-
ari carteziene impuse se obtin valori infinite si/sau nerealizabile pentru coordonatele
articulare, se procedeaza la aproximarea acestor valori cu cele mai apropiate valori finite si/sau realizabile;
3). Generarea traiectoriei se realizeaza folosind functii conducere ( care sunt functii de timp, adica legi de miscare) (matriceale sau nu) ceea ce inseamna ca punctele din spatiu sunt generate, in mod indirect, cu functii de timp. Aceasta metoda constituie ea insasi o metoda de interpolare;
4). Interpolarea liniara (paragraful 11.2.) , de la nivelul executor, impusa de restrictia cu privire la timpul de calcul.
La celelalte metode de conducere nu se folosesc decat o parte dintre niveluri-
le de interpolare mai sus enuntate.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3189
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved