MODELAREA MATEMATICA A MASINII SINCRONE

MODELAREA MATEMATICA A MASINII SINCRONE

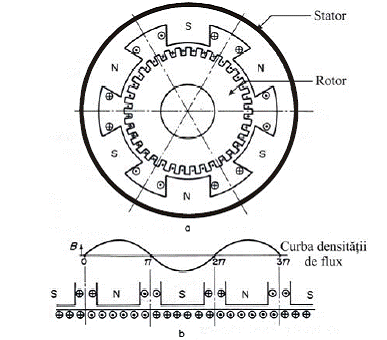
Masinile Sincrone sunt utilizate cu precadere in cazul producerii energiei electrice de aceea in studiul de fata voi considera masina sincrona ca generator, convertind energia mecanica furnizata de o turbina hidraulica sau cu aburi in energie electrica.

Daca p este numarul perechilor de poli, iar n este viteza rotorului in [rot/min], atunci frecventa in [Hz] a t.e.m. induse este:

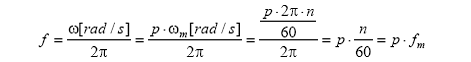
si in regim stationar trebuie sa fie egala cu frecventa retelei electrice la care este conectat generatorul sincron.

1. Modelul electromecanic al generatorului sincron

Prin "ecuatie de miscare" se intelege ecuatia diferentiala care descrie accelerarea/decelerarea rotorului generatorului sincron si a turbinei de antrenare la aparitia unui dezechilibru intre cuplul mecanic si cuplul electromagnetic:

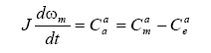
rezultand:

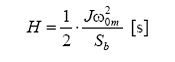
in care ω_0m este viteza unghiulara nominala a rotorului, in radiani mecanici/s.

Daca se exprima momentul de inertie J:

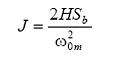
se obtine:

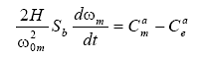
sau:

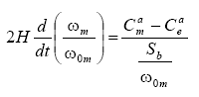
In partea stanga a ecuatiei se tine seama ca:

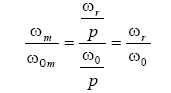
si:

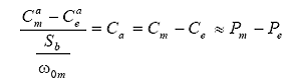
rezulta:

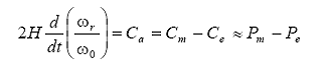
notand:

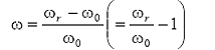
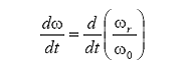
Rezulta:

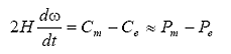
Daca se noteaza cu δ unghiul care determina pozitia rotorului la un moment dat (in radiani electrici) in raport cu un sistem de referinta ce se roteste sincron (cu ω₀) si cu δ₀ valoarea sa la momentul t = 0 atunci:

din care rezulta:

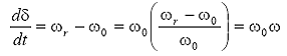
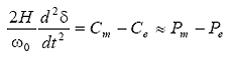
De obicei, ecuatia diferentiala de miscare cuprinde si o componenta a cuplului de amortizare, care se obtine prin adaugarea unui termen proportional cu variatia vitezei unghiulare ω in ecuatia, respectiv:

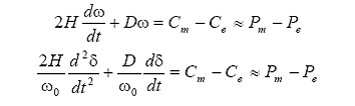
in care D este un coeficient de amortizare (in u.r.).

Obtinem modelul electromecanic al generatorului sincron sub forma urmatoarelor ecuatii diferentiale:

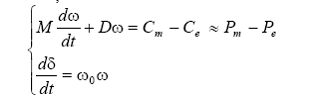
sau

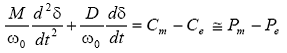
Cand generatorul se afla in punctul de echilibru, viteza unghiulara are valoarea nominala, adica ω_r =ω₀ , respectiv ω= 0 si in consecinta rezulta ca:

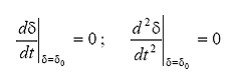
unde δ₀ este unghiul intern in punctul de echilibru.

Schema bloc care reprezinta ecuatia de miscare:

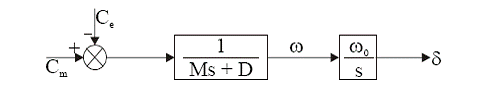
2. Modelul electromagnetic al generatorului sincron

2.1. Ecuatiile de baza ale generatorului sincron

Reprezentarea generatoarelor sincrone printr-un numar de infasurari echivalente, cuplate magnetic si aflate in miscare:

Circuitele statorice: cele 3 infasurari statorice a-a', b-b' si c-c', decalate cu 120^O in sensul trigonometric. Tensiunile la bornele infasurarilor statorice sunt ua , ub si uc, iar curentii ia ,ib si ic. Se va utiliza conventia de la generator, adica curentul din stator este pozitiv cand iese din masina.

Circuitele rotorice. Infasurarea de excitatie f-f', a carei axa se numeste directa (axa d) sau longitudinala. Axa perpendiculara pe axa directa - defazata cu 90⁰ inainte in sensul de rotatie - se numeste axa q, in cuadratura sau transversala. In acest caz se spune ca "axa q conduce axa d" (Standard american IEEE 100-1977). Alegerea sensului pozitiv al axei q este arbitrara. In afara de aceasta, se considera infasurarile de amortizare dispuse dupa cele doua axe rotorice. Numarul acestor infasurari caracterizeaza gradul de precizie al modelului generatorului. Modelele cele mai utilizate folosesc cate o infasurare de amortizare in axa d notata cu D, respectiv in axa q notata cu Q. Aceste infasurari sunt in permanenta scurtcircuitate.

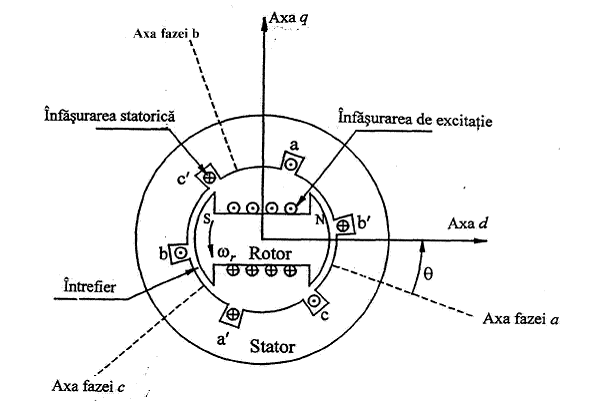
Daca aplic legea inductiei electromagnetice rezulta urmatoarele ecuatii ale tensiunilor in marimi instantanee.

. Pentru infasurarile statorice:

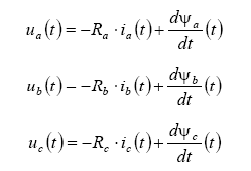
unde: Ra, Rb, Rc sunt rezistentele ohmice ale fazelor a, b, respectiv c; ψ - fluxul total care inlantuie o faza.

Aceste relatii se pot scrie sub forma matriceala:

unde:

. Pentru infasurarile rotorice:

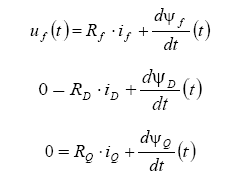
sau sub forma matriceala:

unde:

2.2. Ecuatiile fluxurilor magnetice

Fluxul total ce inlantuie infasurarea statorica a fazei "a" in orice moment se poate exprima sub forma:

In mod similar se pot scrie expresiile fluxurilor din infasurarile statorice b si c, respectiv, din celelalte infasurari ale generatorului sincron, rezultand:

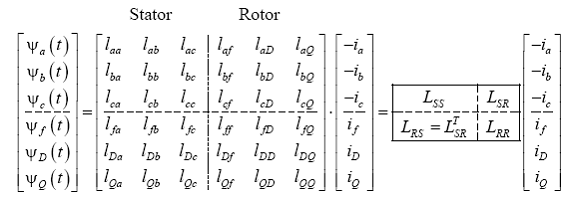
3. Modelul matematic al generatorului sincron

In urma inlocuirii celor trei infasurari statorice prin cele trei infasurari rotorice fictive denumite d, q, 0 (sistem de coordonate rotorice), conform figurii de mai jos:

infasurarile din axele d (longitudinala) si q (transversala) se rotesc impreuna cu rotorul. Nu exista cuplaje mutuale intre infasurarile dupa axele d si q;

axa 0 este independenta de axele d si q, fiind parcursa de curenti numai in regim dezechilibrat.

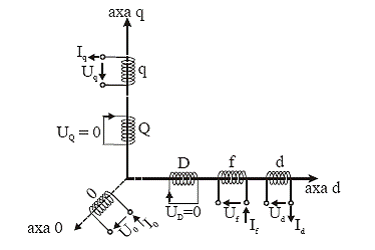
Daca se considera ecuatiile ale fluxurilor din infasurarile circuitelor rotorice:

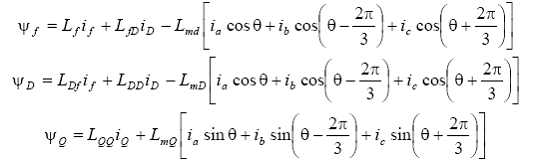
se observa ca, curentii de faza statorici se combina in forme asemanatoare in fiecare axa. Aceasta sugereaza transformarea curentilor de faza statorici in noi variabile de stare. Astfel, se propun pentru noii curenti in axele d, q, 0 relatiile:

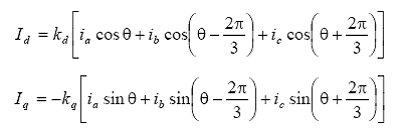
Constantele kd si kq sunt arbitrare si valorile lor pot fi alese pentru a simplifica coeficientii in ecuatiile de functionare. In majoritatea studiilor de specialitate asupra teoriei masinii sincrone, coeficientii kd si kq au valorile 2/3 si in prezentul studiu voi alege in acelasi fel. O alternativa a transformarii poate fi cu

Daca as alege

se poate arata ca, pentru regimuri sinusoidale si echilibrate ale generatorului sincron, valorile de varf ale curentilor Id si Iq sunt egale cu valoarea de varf a curentului statoric. In acest scop se considera expresiile corespunzatoare curentilor din stator pentru un regim echilibrat:

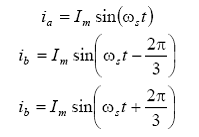
unde viteza unghiulara a curentilor statorici in radiani electrici/secunda este:

Daca se inlocuiesc aceste expresii in ecuatiile rezulta:

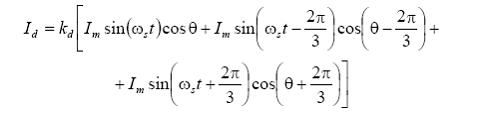
sau dupa efectuarea transformarilor trigonometrice:

Pentru ca valoarea de varf a curentului Id sa fie egala cu Im , coeficientul kd trebuie luat egal cu 2/3. In mod similar din ecuatia, pentru conditii de incarcare echilibrata, rezulta:

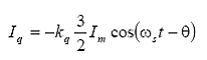
Din nou, pentru ca valoarea maxima a lui I_q sa fie egala cu valoarea de varf a curentului statoric trebuie ca k_q = 2/3.

Deoarece cele doua componente ale curentului Id si Iq produc impreuna un camp magnetic identic cu cel produs de setul original al celor 3 curenti de faza, rezulta ca cea de a treia componenta nu trebuie sa produca nici un camp in spatiul intrefierului. Deci, cea de a treia variabila convine a fi curentul de secventa zero I₀, adoptat prin analogie cu componenta de secventa zero din teoria componentelor simetrice:

Daca regimul este echilibrat:

I este o valoare instantanee a curentului care poate varia cu timpul.

Deci, transformarea Park de la variabilele de faza, la variabilele d,q,0 poate fi scrisa pentru curenti sub urmatoarea forma matriceala:

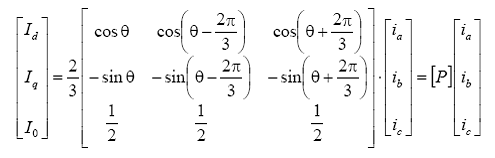
Transformarea inversa de la variabilele d,q,0 la variabilele a,b,c este data de expresiile:

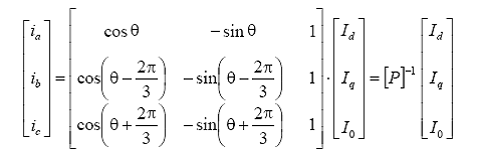
3.1. Exprimarea fluxurilor din infasurarile statorice in componente d,q,0

Ecuatiile fluxurilor magnetice din infasurarile statorice si rotorice se pot scrie sub forma matriceala:

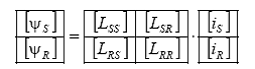
Aplicand transformata inversa pentru curenti in membrul drept, rezulta:

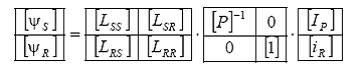
unde:

Aplicand transformata Park directa fluxurilor magnetice se obtine:

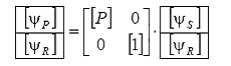
unde:

Din relatiile de mai sus rezulta:

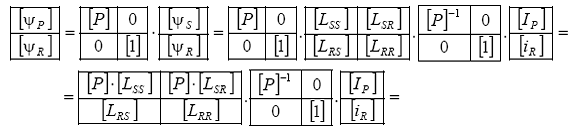
Efectuand inlocuirile corespunzatoare si realizand calculele (inclusiv reducerile trigonometrice) rezulta:

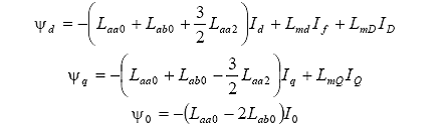
Se mentioneaza ca desi curentii rotorici nu sufera nici un fel de modificare, din considerente de uniformizare a scrierii s-au folosit majuscule If, ID, IQ in loc de if, iD, iQ. Daca definim noi inductivitati:

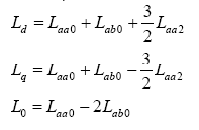
sau:

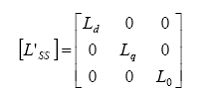
atunci expresiile fluxurilor magnetice statorice in coordonate d,q,0 devin:

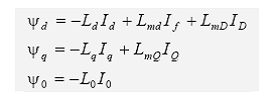
Rezulta, de asemenea:

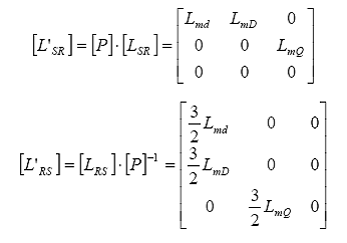
Se observa ca de aceasta data componentele d,q,0 ale fluxurilor statorice sunt legate de componentele curentilor statorici si rotorici prin inductivitati constante.

3.2. Exprimarea fluxurilor din infasurarile rotorice in componente d,q,0

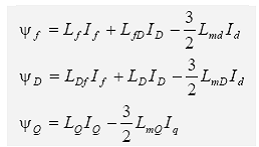
Se constata ca si inductivitatile sunt constante, adica, sunt independente de pozitia rotorului (cu mentiunea ca nu au fost considerate efectele saturatiei!). Este interesant de observat ca I0 nu apare in ecuatiile fluxurilor rotorice. Aceasta se datoreaza faptului ca, componentele de secventa zero ale curentului statoric nu produc forte magnetomotoare in interiorul intrefierului.

Trebuie subliniat faptul ca, desi prin transformarea d,q,0 se obtin inductivitati constante in ecuatiile fluxurilor statorice si rotorice, inductivitatile mutuale intre infasurarile statorice si rotorice nu mai sunt reciproce! De exemplu, inductivitatea mutuala asociata cu fluxul care inlantuie infasurarea de excitatie, datorat curentului Id din infasurarea statorica d, este L_md , inductivitatea mutuala asociata cu fluxul care inlantuie infasurarea d, datorat campului produs de curentul de excitatie If, este Lmd (adica fara coeficientul 3/2).

3.3. Ecuatiile tensiunilor la bornele infasurarilor statorice in componente d,q,0

Se considera ecuatiile tensiunilor statorice ale celor trei faze, respectiv, forma matriceala a acestora:

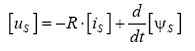
in care:

reprezinta rezistenta ohmica a unei infasurari statorice.

Aplicand transformata Park rezulta:

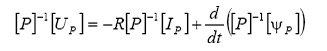
Deoarece [P]⁻¹ este functie de unghiul θ, ultimul termen din membrul drept poate fi exprimat sub forma:

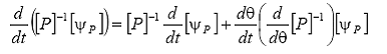
unde:

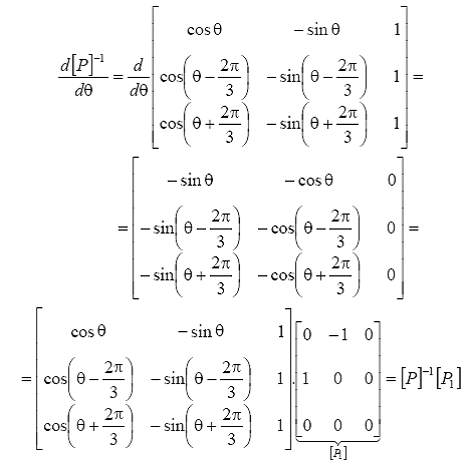
unde [P] este un operator de rotatie cu 90⁰ in planul d - q.

Tinand seama de ecuatiile de mai sus se poate scrie:

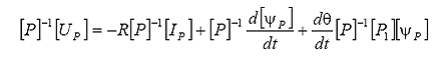
cu ajutorul operatorului P se obtine:

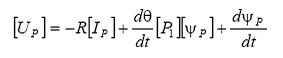
Dezvoltand ecuatia de mai sus rezulta:

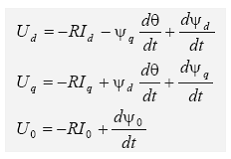
3.4. Ecuatiile tensiunilor la bornele infasurarilor rotorice

Circuitele rotorice, care raman neschimbate prin aplicarea transformatei Park, sunt descrise de ecuatiile:

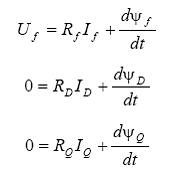
unde: Uf este tensiunea aplicata infasurarii de excitatie; Rf - rezistenta ohmica a infasurarii de excitatie; RD, RQ - rezistentele ohmice ale infasurarilor de amortizare.

Daca se renunta la circuitul de secventa 0 (in regimuri simetrice echilibrate) si se regrupeaza pe de o parte circuitele d,f,D si pe de alta parte circuitele q, Q, atunci ecuatiile Park care descriu comportamentul generatorului sincron se scriu sub forma:

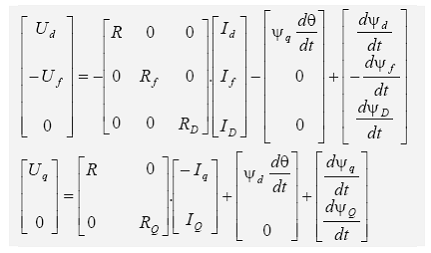
cu relatiile de legatura intre fluxuri si curenti:

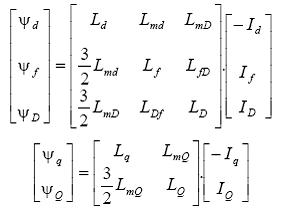
3.5. Puterea si cuplul electric

Puterea trifazata instantanee la bornele statorului este:

Eliminand tensiunile si curentii de faza prin exprimarea sub forma componentelor d,q,0 se obtine:

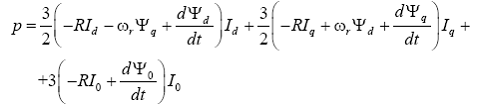
sau, dupa efectuarea calculelor si rearanjare, se obtine:

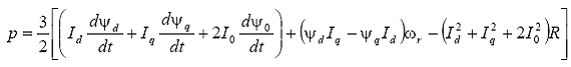
Cuplul electromagnetic in intrefier Ce se obtine prin impartirea puterii transferate prin intrefier (adica puterea corespunzatoare t.e.m. de rotatie) la viteza de rotatie in radiani mecanici/secunda:

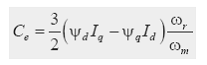
Influenta saturatiei magnetice

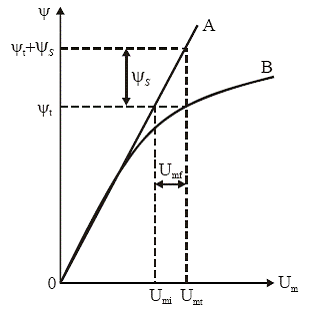
In dezvoltarea ecuatiilor de baza ale generatorului sincron si analiza caracteristicilor sale am neglijat efectele saturatiei magnetice a fierului statoric si rotoric. Totusi, dupa cum este cunoscut, in cazul unui circuit feromagnetic apare fenomenul de saturare a fierului care conduce la neliniaritati puternice. Astfel, in cazul general al circuitelor magnetice cu intrefier, de tipul celor prezente in masinile sincrone, pentru care calea de inchidere a fluxului magnetic cuprinde fierul magnetic si aerul intrefierului, intre fluxul magnetic si forta sau tensiunea magnetomotoare (t.m.m.) U_m exista o relatie de dependenta reprezentata de caracteristicile din figura de mai jos.

In absenta saturatiei fierului magnetic, aceasta dependenta este reprezentata de dreapta OA numita linia sau caracteristica intrefierului In acest caz reluctanta circuitului magnetic este dominata de reluctanta aerului din intrefier. In realitate, pe masura ce tensiunea magnetomotoare creste, fierul se satureaza, iar caracteristica se abate de la linia intrefierului urmand curba de saturatie OB a acestuia. Tensiunea magnetomotoare U _mt necesara obtinerii unei valori date a fluxului total se compune din tensiunea magnetomotoare corespunzatoare liniei intrefierului fierului magnetic U _mf , adica: .

In aceste conditii, gradul de saturare a fierului magnetic poate fi cuantificat prin factorul sau coeficientul de saturare K _S definit ca raportul dintre tensiunea magnetomotoare necesara obtinerii fluxului total in absenta saturatiei si tensiunea magnetomotoare necesara obtinerii aceluiasi flux considerand si efectul saturatiei. Prin urmare rezulta:

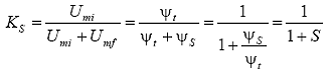
in care este functia de saturare a fierului magnetic.

Prin neglijarea saturatiei se obtin relatii de dependenta liniara intre fluxurile magnetice, respectiv tensiunile electromotoare si curentii corespunzatori care, in cazul generatorului sincron, simplifica foarte mult efortul de calcul. In schimb considerarea fenomenului de saturare a fierului magnetic, prin neliniaritatile puternice pe care le introduce, face mult mai complicata analiza regimurilor de functionare. In aceste conditii, din perspectiva analizei comportamentului dinamic, o tratare riguroasa a efectelor saturatiei generatorului sincron este inadecvata, deoarece, in general, nu se dispune de datele necesare. In practica sunt utilizate metode aproximative pentru a reprezenta saturatia magnetica. Acestea se bazeaza pe un set de ipoteze simplificatoare menite sa asigure un optim intre structura modelului dezvoltat, datele disponibile si acuratetea rezultatelor obtinute .

Caracteristicile de mers in gol si scurtcircuit

In particular pentru un generator sincron, datele esentiale necesare tratarii saturatiei sunt furnizate de caracteristicile de mers in gol si scurtcircuit trasate pe baza incercarilor de mers in gol si scurtcircuit.

Caracteristica de mers in gol CMG reprezinta variatia tensiunii U la bornele generatorului sincron in functie de curentul de excitatie I _f in conditiile functionarii in gol la viteza nominala. Tinand cont ca in regimul de mers in gol valoarea curentului este zero, adica , din ecuatiile generatorului sincron se obtin egalitatile:

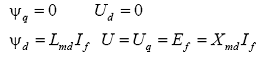
din care, avand in vedere ca in unitati relative viteza unghiulara este , rezulta ca fluxul si tensiunea la borne U , exprimate in unitati relative, au valori egale si, prin urmare, caracteristica de mers in gol reprezinta fie variatia tensiunii la borne, fie variatia fluxului in functie de curentul de excitatie.

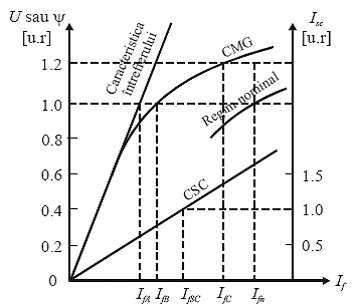
O caracteristica tipica de mers in gol este prezentata in figura de mai jos. Se constata ca pentru valori ale tensiunii la bornele generatorului mai mici decat 0,8; in unitati relative, saturatia este practic inexistenta, iar caracteristica de mers in gol urmeaza linia intrefierului indicand curentul de excitatie necesar pentru a invinge rezistenta magnetica (reluctanta) acestuia.

In schimb, pentru valori ale tensiunii la borne mai mari decat 0.8 u.r., apare fenomenul de saturare magnetica si prin urmare, caracteristica de mers in gol se abate de la linia caracteristica intrefierului. Avand in vedere relatiile regimului de mers in gol rezulta ca aceasta abatere constituie o indicatie a gradului de saturare din axa d a generatorului sincron.

Caracteristica de scurtcircuit CSC reprezinta variatia curentului statoric in functie de curentul de excitatie I _f atunci cand generatorul functioneaza in regim permanent la turatie nominala, iar bornele statorice sunt scurtcircuitate. O caracteristica de scurtcircuit (CSC) este, de asemenea, prezentata in figura anterioara. Aceasta este liniara pana la si dincolo de curentul nominal statoric, deoarece in conditii de scurtcircuit nominal, exista o saturatie in fier foarte mica datorita efectului de demagnetizare al reactiei statorului.

In regim de scurtcircuit, daca se neglijeaza rezistenta infasurarilor statorice, tensiunea la borne fiind egala cu zero (  ), din ecuatiile regimului permanent al generatorului sincron rezulta ca tensiunea electromotoare indusa este:

si, prin urmare, valoarea nesaturata a reactantei sincrone longitudinale, data de relatia

, este constanta.

Este evident faptul ca in prezenta saturatiei magnetice raportul E_f/I_SC nu ramane constant, ci descreste odata cu cresterea excitatiei. Astfel, reactanta sincrona longitudinala nu mai este un parametru independent al generatorului sincron, ci ia diferite valori in functie de regimul de functionare.

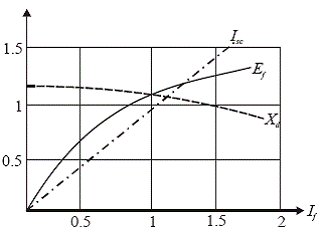
Daca se neglijeaza anizotropia rotorica (X_d=X_q=X_S) si se tine cont de faptul ca tensiunea electromotoare indusa este direct proportionala cu intensitatea curentului de excitatie, atunci relatia poate fi scrisa sub forma:

Deoarece in regim de scurtcircuit nominal I _SC  1 u.r. , iar curentul de excitatie corespunzator este I_fSC rezulta:

in care X _{S, nsat} este reactanta sincrona nesaturata.

Pe de alta parte, considerand ca in regimul de mers in gol tensiunea la borne este egala cu 1 u.r., in conformitate cu valoarea curentului de excitatie corespunzator acestei tensiuni, pe caracteristica intrefierului, este I_fA si deci KI _fA . Tinand cont de aceasta egalitate, se obtine valoarea nesaturata a reactantei sincrone:

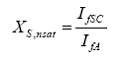
Daca se considera efectul saturatiei, atunci, conform figurii, pentru a obtine o tensiune la borne egala cu 1 u.r. (tensiunea nominala la mersul in gol) este necesara o valoare a curentului de excitatie I_fB>I_fA, iar valoarea saturata a reactantei sincrone este:

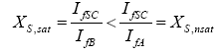
In concluzie, in cazul unei caracteristici nelineare a regimului de mers in gol, valorile reactantei sincrone X_d pe care trebuie sa le luam in considerare in evaluarea stabilitatii statice in conditiile normale de functionare ale generatorului, nu coincid perfect cu valorile X_d pe care le obtinem din incercarea de scurtcircuit; totusi, caracterul variatiei lui X_d micsorarea lui pentru curenti mari de excitatie - se pastreaza si in aceste conditii.

In general, in tabelele cu reactantele sincrone ale generatoarelor sunt date intotdeauna valorile reactantelor nesaturate. Pentru evaluarea stabilitatii statice, in calculul caracteristicilor de putere, etc. aceste valori trebuie micsorate cu cel putin

.

La masinile cu poli inecati si intrefier uniform de-a lungul intregii circumferinte a rotorului, saturatia are aceeasi influenta atat asupra reactantei sincrone longitudinale, cat si asupra celei transversale. In schimb la generatoare cu poli aparenti, valoarea mai mare a intrefierului de-a lungul axei transversale q, elimina influenta caracteristicii fierului asupra reactantei sincrone transversale practic aceasta nedepinzand de saturatie.

Raportul de scurtcircuit (RSC), definit ca raportul dintre curentul de excitatie I_fB necesar obtinerii tensiunii nominale pe caracteristica de mers in gol si curentul de excitatie I_fSC necesar obtinerii curentului statoric nominal pe caracteristica de scurtcircuit, adica este un indicator care reflecta gradul de saturatie a generatorului sincron si are o importanta practica atat in raport cu functionarea cat si cu costul acesteia. Astfel, RSC este cu atat mai mic cu cat gradul de saturare este mai redus si are o valoare minima, egala cu inversul reactantei X _{s ,nsat} in absenta saturatiei.

Din punct de vedere functional, o valoare redusa a raportului RSC indica faptul ca pentru a mentine tensiunea la borne, in conditiile unei modificari date a sarcinii, este necesara o variatie mare a curentului de excitatie, adica un sistem de excitatie performant capabil sa realizeze modificari mari ale curentului de excitatie pentru a mentine stabilitatea.

4.2. Reprezentarea saturatiei

Pentru a reprezenta saturatia circuitelor magnetice ale generatorului sincron este necesara o metoda simpla de determinare a factorului de saturare K_S , pentru orice regim de functionare si de introducere a acestuia in calculul parametrilor generatorului sincron. In acest sens, se admit in mod uzual urmatoarele ipoteze simplificatoare

Inductivitatile, respectiv reactantele de scapari sunt independente de saturatie pentru ca traseul fluxurilor de scapari este preponderent prin aer. Deci, singurele inductivitati afectate de fenomenul de saturare sunt inductivitatile mutuale sau de magnetizare L_md si L_mq.

) Fluxurile de scapari nu contribuie la saturatia fierului deoarece au, in mod uzual, valori mici, iar traseul lor coincide cu cel al fluxului principal numai pe o mica portiune. Prin urmare, saturatia este determinata de fluxul util din intrefier.

Caracteristica de mers in gol CMG este utilizata pentru a estima saturatia si la functionarea in sarcina pentru ca este practic singurul element care furnizeaza informatii relative la fenomenul de saturare a generatorului sincron.

Nu exista nici un cuplaj magnetic intre axele d si q ca rezultat al nelinearitatilor introduse de saturatie.

Cu aceste ipoteze, efectele saturatiei pot fi reprezentate prin:

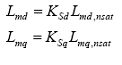
unde L_{md nsat} si L_{mq nsat} sunt valorile nesaturate ale inductivitatilor L_md si L_mq. Factorii de saturatie K_Sd si K_Sq se identifica cu gradele de saturare din axe d si respectiv q.

In conformitate cu ipoteza factorul de saturare in axa d se determina pornind de la caracteristica de mers in gol (GMG). Astfel, pentru un punct de functionare a, caracterizat de curentul de excitatie I_f,a si fluxul tinand cont de relatia de definitie a factorului de saturare si de asemanarea triunghiurilor care se formeaza rezulta:

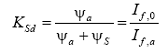
In ceea ce priveste determinarea gradului de saturare in axa q se au in vedere urmatoarele aspecte:

- Pentru masinile cu poli aparenti (hidrogeneratoarele), deoarece calea de inchidere a fluxului este in mare majoritate prin aer, saturarea fierului in lungul acestei axe este nesemnificativa si prin urmare se poate aproxima K_Sq = 1

- Pentru masinile cu poli inecati (turbogeneratoarele) exista saturatie magnetica si in axa q iar factorul K_Sq ar trebui determinat din caracteristica de magnetizare in lungul acestei axe. Deoarece datele referitoare la aceasta caracteristica nu sunt disponibile (prin incercarea de mers in gol se obtine caracteristica de magnetizare in lungul axei d se poate aproxima, cu suficienta precizie, . Aceasta aproximatie este echivalenta cu ipoteza ca intrefierul, respectiv reluctanta caii magnetice sunt uniforme in lungul periferiei rotorice. Caracteristica de saturare a Generatorului Sincron la mers in gol.

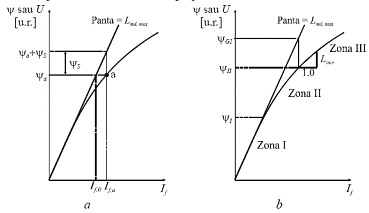
Avand in vedere cele prezentate anterior, rezulta ca pentru a reprezenta efectele saturatiei este necesara stabilirea unei expresii matematice care sa cuantifice abaterea curbei de magnetizare de la linia intrefierului. In acest sens, caracteristica CMG este impartita in trei zone

Zona I, corespunzatoare zonei in care nu se produce fenomenul de saturare, este caracterizata de valori ale fluxului mai mici decit o valoare de prag care in mod uzual este 0.8 u.r.;

Zona II, corespunzatoare unei saturatii partiale a fierului magnetic, este caracterizata de valori ale fluxului mai mari decat si mai mici ca . Valoarea de prag

peste care se produce saturarea completa a circuitului magnetic este in mod uzual egala cu 1,2 u.r.;

Zona III, corespunzatoare saturarii totale a circuitului magnetic, este caracterizata de valori ale fluxului mai mari decat valoarea de prag . Pentru zona I definita de , rezulta:

Pentru zona II definita prin , poate fi exprimat printr-o functie exponentiala de forma:

in care A_S si B_S sunt constante ce depind de caracteristica saturatiei in portiunea zonei II

In cazul in care din ecuatie rezulta si deci , aceasta reprezentare conduce la o mica discontinuitate la jonctiunea dintre zonele I si II. Totusi, pentru ca in mod normal A_S are o valoare foarte mica, rezulta o discontinuitate nesemnificativa.

Pentru zona III definita prin , abaterea de la curba intrefierului poate fi evaluata cu expresia:

in care

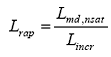
Prin aceasta metoda, caracteristica saturatiei pentru orice generator sincron este complet specificata prin parametrii:

Valorile celor doua componente ale fluxului util din intrefier sunt date de expresiile:

Daca se multiplica relatiile de mai sus cu ω_r si se tine seama de ecuatiile statorice:

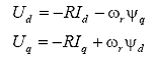
rezultate prin neglijarea t.e.m. de transformare

,

se obtine:

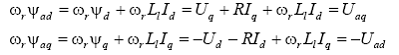
din care rezulta:

respectiv:

In unitati relative, avand in vedere ca ω_r = 1 din relatiile de mai sus rezulta ca fluxul total ψ_at este egal cu modulul tensiunii din intrefier U _a .

In aceste conditii, pentru un regim de functionare oarecare caracterizat de calculul coeficientilor de saturare K_Sd si K_Sq se efectueaza conform urmatorului algoritm: