Momentul unei forte in raport cu un punct

Momentul unei forte in raport cu un punct

Definitia 2.16:

Momentul unei forte in raport cu un punct O numit pol, este dat de produsul vectorial dintre vectorul de pozitie al punctului de aplicatie A al fortei si vectorul forta .

(2.29)

Fig. 2.7.

Momentul este un vector legat, aplicat in punctul O, care are, corespunzator definitiei, directia perpendiculara pe planul format de vectorii si , sensul dat de regula burghiului drept si modulul dat de relatia

(2.30)

In relatia (2.30), d se numeste bratul fortei si reprezinta distanta de la punctul O la dreapta suport a fortei , iar a reprezinta unghiul dintre dreptele suport ale vectorilor si .

Intr-un sistem cartezian triortogonal, cand vectorii si sunt dati prin componentele lor, respectiv , expresia analitica a momentului unei forte in raport cu un punct O numit pol,

(2.31)

este data de relatia

(2.32)

Identificand membru cu membru relatiile (2.31) si (2.32), se obtin expresiile proiectiilor momentului, , unei forte in raport cu un punct, pe axele sistemului cartezian de coordonate

(2.33)

Momentul, , unei forte in raport cu un punct, se bucura de toate proprietatile produsului vectorial, la care se

adauga:

este nul daca produsul vectorial este nul (, , ) sau, cu alte cuvinte, cand punctul O se afla pe dreapta suport a fortei.

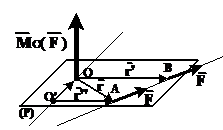
Fig. 2.8.

este invariant la operatia de lunecare a fortei pe dreapta sa suport. Intr-adevar, analizand Figura 2.8,

deoarece , vectorii si fiind coliniari.

variaza daca se schimba pozitia polului din O in O', dreapta suport a fortei ramanand neschimbata. Intr-adevar, analizand Figura 2.8,

Observatia 2.2:

Daca polul O se deplaseaza pe o dreapta paralela cu dreapta suport a fortei, atunci momentul fortei in raport cu acest punct numit pol, este invariant la schimbarea pozitiei sale.

intre proiectiile fortei pe axele sistemului cartezian de

coordonate si proiectiile momentului dat de aceasta forta in raport cu punctul O, pe axele aceluiasi sistem de axe de coordonate, exista o relatie scalara identic satisfacuta si care exprima perpendicularitatea celor doi vectori

sau, dezvoltat,

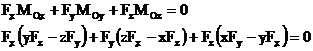
Observatia 2.3:

Proiectiile fortei pe axele sistemului cartezian de coordonate si proiectiile momentului dat de aceasta forta in raport cu punctul O, pe axele aceluiasi sistem de axe de coordonate, caracterizeaza vectorul ca vector alunecator.

Momentul fortei in raport cu un punct ramanand acelasi cand forta aluneca pe suportul ei, permite folosirea lui pentru indicarea suportului fortei. Acest suport se afla intr-un plan perpendicular pe directia momentului, la distanta 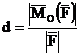si de acea parte a lui O care corespunde sensului momentului (forta aflata pe acest suport trebuie sa roteasca burghiul astfel incat el sa inainteze in sensul momentului).