| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
TERMOTEHNICA SI MASINI TERMICE
Notiuni introductive
Termotehnica - ramura de stiinta care se ocupa cu studiul teoriei si mijloacelor de transfer a energiei termice, obtinerea ei precum si transformarea acestei energii in alte forme de energie (de exemplu mecanica).
In 1894 Carnot defineste termodinamica drept forta motoare a caldurii. Termodinamica este o ramura a fizicii caare se ocupa cu studiul fenomenelor in care variatia temperaturii joaca un rol primordial. Aceste fenomene implica miscarea termica a materiei - miscarea browniana intensificata de cresterea temperaturii - si transformarea energiei dintr-o forma in alta.
Masinile termice sunt acele masini care transforma o forma de energie in alta ca o aplicatie practica a proceselor termodinamice. In general, termenul de masina implica un sistem format din mai multe corpuri, care au miscari determinate unele fata de celelalte, utilizat pentru transformarea energiei dintr-o forma in alta dintre care una este energie mecanica.
Sisteme termodinamice - totalitatea corpurilor care interactioneaza din punct de vedere termic si mecanic atat intre ele cat si cu mediiul exterior. Sistemul termodinamic este un sistem material - continuu - care schimba energie sub forma de lucru mecanic si caldura. Sistemele pot sa fie: a) inchise care la randul lor sunt sisteme izolate sau neizolate si b) sisteme deschise.
Sistemul inchis este cel care nu schimba materie cu exteriorul, iar sistemul izolat este acela care nu are schimb de energie termica cu exteriorul. La sistemele neizolate apare o interactiune cu mediul inconjurator prin cedare si captare de energie termica.
Sistemul omogen este acela care are o distributie uniforma a proprietatilor in tot spatiul ocupat de mediul continuu - de exemplu densitatea, temperatura etc.
Sistemul eterogen este acel mediu continuu la care distributia proprietatilor nu mai este uniforma in tot domeniul.
Stare termodinamica reprezinta starea unui sistem definita prin marimile macroscopice la un moment dat - ansamblul valorilor temperaturii T, a volumului V, presiunii p si masei m a corpului.
Marimile de stare se refera la starea termodinamica a unui corp. Parametri de stare folositi in termodinamica sunt:
a) fizici: temperatura T, volumul V, presiunea p;
b) calorici: energie interna, entalpie si entropie.
Orice stare macroscopica este rezultatul starilor microscopice dependente de miscarile globale, haotice ale moleculelor, atomilor in cadrul miscarii browniene - denumita agitatie termica. Starea microscopica se poate schimba fara ca acest fapt sa se reflecte in starea macroscopica. Apare astfel notiunea de probabilitate termodinamica. Probabilitatea termodinamica se refera la probabilitatea de realizare a unei stari microscopice care se reflecta la un moment dat intr-o stare macroscopica.
Starea de echilibru - se realizeaza atunci cand conditiile exterioare sunt constante si se caracterizeaza prin repartizarea uniforma a presiunii, temperaturii si densitatii in toate punctele unui sistem, temperatura si presiunea fiind identice cu cele ale mediului ambiant.
Starea de echilibru termodinamica este starea de echilibru in care nu se realizeaza schimb de energie intre partile componente ale unui sistem, iar starea sistemului ramane constanta in timp. Modificarea conditiilor exterioare va produce intotdeauna modificarea starii sistemului. De aceea in interiorul unui sistem se va produce un schimb de energie pentru restabilirea repartizarii uniforme a parametrilor respectivi.
Timp de relaxare - timpul necesar restabilirii repartitiei uniforme a parametrilor de stare; acest timp este dependent de starea si natura corpului.
Transformarea termodinamica - trecerea sistemului de la o stare termodinamica la alta. Dupa modul cum se parcurge transformarea acestea pot fi:
a) reversibile - transformarea se realizeaza spontan in ambele sensuri cu parcurgerea acelorasi stari intermediare care intotdeauna sunt stari de echilibru;
b) ireversibile - transformarea se realizeaza intr-un singur sens cu modificarea parametrilor de stare.
In masinile termice agentul de lucru este un gaz. Dupa modul cum se considera comportarea lor gazele sunt perfecte sau reale. De cele mai multe ori, pentru simplitate, gazele se considera perfecte.
Gazul perfect - este format din molecule sferice, perfect elastice, lipsit de forte de coeziune moleculara,cu molecule monoatomice in miscare de translatie si cu distributia ciocnirilor dintre molecule stationara. In general, legile stabilite pentru gazele perfecte dau rezultate satisfacatoare in calculele termodinamice pentru domeniul presiunilor si temperaturilor scazute si medii. Pentru gazul perfect 1 kmol are intotdeauna numarul de molecule dat de Avogadro NA = 6,023 1026 molecule/kmol.
Pentru
gazl perfect este valabila legea ![]() (1)
(1)
unde VN este volumul molar normal, iar k este constanta lui Boltzman.
Deoarece
volumul molar la o presiune si temperatura data nu depinde de
natura gaului s epoate scrie legea ![]() (2) in care Rm este constanta
gazelor perfecte cu valoare unica pentru toate gazele.
(2) in care Rm este constanta
gazelor perfecte cu valoare unica pentru toate gazele.
Starea normala fizica a uni gaz este definita prin valorile pN = p0 = 760 mmHg = 1 At = 101325 N/m2, tN = t0 = 00 C. In aceste conditii de presiune si temperatura 1 kmol din orice gaz perfect ocupa un volum egal cu volumul molar normal VN = 22,414 Nm3/kmol. Cu aceste valori rezulta constanta gazelor perfecte Rm= 8315 J/kmol si grad Kelvin. Ea reprezinta lucrul mecanic pe care-l efectueaza un kmol de gaz in cursul careia temperatura variaza cu un grad Kelvin.
Pentru
o masa de 2 kg de gaz perfect relatia 1 rezulta sub forma ![]() (3) ecuatia lui Clapeyron care face
legatura intre principalele marimi de stare. Constanta gazelor
perfecte este R = Rm/M [J/kg K], unde R este constanta
unui gaz anume - cu valori dependente de natura gazului, iar M este masa
moleculara aparenta a gazului M[kg/kmol]. Constanta R
repreziinta lucrul mecanicefectuat de 1 kg de gaz pentru a-si varia
temperatura cu un grad Kelvin.
(3) ecuatia lui Clapeyron care face
legatura intre principalele marimi de stare. Constanta gazelor
perfecte este R = Rm/M [J/kg K], unde R este constanta
unui gaz anume - cu valori dependente de natura gazului, iar M este masa
moleculara aparenta a gazului M[kg/kmol]. Constanta R
repreziinta lucrul mecanicefectuat de 1 kg de gaz pentru a-si varia
temperatura cu un grad Kelvin.
Daca
se considera intreaga cantitate de gaz m perfecta se poate scrie o
alta forma a relatiei 2 de forma ![]() (4) care reprezinta ecuatia de
stare pentru intreaga cantitate de gaz ce evolueaza in procesul
termodinamic. In relatia de mai sus apare volumul specific
(4) care reprezinta ecuatia de
stare pentru intreaga cantitate de gaz ce evolueaza in procesul
termodinamic. In relatia de mai sus apare volumul specific ![]() [m3/kg] dat
de
[m3/kg] dat
de ![]() - inversul
densitatii.
- inversul
densitatii.
TERMODINAMICA GENERALA
Coeficienti termodinamici
In
termodinamica se lucreaza cu trei parametri de stare fizica:
presiune, volum, temperatura. Pentru o masa de 1 kg de gaz perfect
parametrii de stare se pot exprima sub forma literelor p, ![]() , T. Se poate considera ca exista o functie
implicita care face legatura intre cei trei parametri rezultand o
ecuatie de stare de forma
, T. Se poate considera ca exista o functie
implicita care face legatura intre cei trei parametri rezultand o
ecuatie de stare de forma ![]() - ce se poate
reprezenta intr-un spatiu cu trei dimensiuni - o suprafata
spatiala. Ca urmare se pot considera functiile de doua
variabile cu care se poate lucra mult mai usor deoarece reprezentarea
grafica se realizeaza in spatiul bidimensional
- ce se poate
reprezenta intr-un spatiu cu trei dimensiuni - o suprafata
spatiala. Ca urmare se pot considera functiile de doua
variabile cu care se poate lucra mult mai usor deoarece reprezentarea
grafica se realizeaza in spatiul bidimensional ![]() ;
; ![]() ;
; ![]() ; aceste functii admit diferentiale totale exacte.
Prin derivarea lor se obtine
; aceste functii admit diferentiale totale exacte.
Prin derivarea lor se obtine
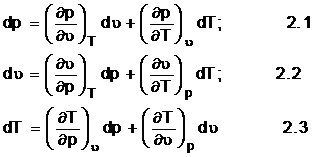
Toate marimile de stare admit diferentiale totale exacte pentru ca ele se refera la un mediu continuu. Derivatele partiale din 2.1, 2.2, 2.3 au semnificatii fizice - viteza de variatie a marimii respective in raport cu marimea de derivare.
In
general, intr-o transformare de stare se produce variatia a unui sau a doi
parametri, exceptand cazul special al evolutiei simultane a tuturor celor
trei parametri p, ![]() , T. Daca se considera pe rand constanta unui
parametru de stare se poate deduce semnificatia fizica a derivatelor
partiale pentru care va rezulta apoi semnificatia coeficientilor.
, T. Daca se considera pe rand constanta unui
parametru de stare se poate deduce semnificatia fizica a derivatelor
partiale pentru care va rezulta apoi semnificatia coeficientilor.
Transformarea izocora.
Transformarea apare atunci cand volumul de gaz este constant ![]() = constant de unde
rezulta diferentiala d
= constant de unde
rezulta diferentiala d![]() = 0. Din diferentiala totala 2.1 se obtine
= 0. Din diferentiala totala 2.1 se obtine 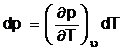 . Se raporteaza variatia presiunii la presiunea
initiala p0, corespunzatoare temperaturii
initiale T0 si rezulta coeficientul
. Se raporteaza variatia presiunii la presiunea
initiala p0, corespunzatoare temperaturii
initiale T0 si rezulta coeficientul 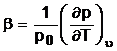 (2.4) denumit coeficient izocor de variatie a presiunii.
(2.4) denumit coeficient izocor de variatie a presiunii.
Transformarea izobara. Transformarea
izobara apare atunci cand presiunea in volumul de gaz este constanta
p = constant, cu derivata dp = 0. Din diferentiala totala exacta
2.2 se obtine 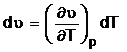 . Se raporteaza variatia volumului la volumul
initial
. Se raporteaza variatia volumului la volumul
initial ![]() 0, corespunzator temperaturii initiale T0
si rezulta coeficientul
0, corespunzator temperaturii initiale T0
si rezulta coeficientul 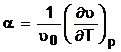 (2.5) denumit coeficient izobar de dilatare volumica. Valorile acestui
coeficient sunt dependente de temperatura si mai ales de natura
gazului care este supus transformarii izobare.
(2.5) denumit coeficient izobar de dilatare volumica. Valorile acestui
coeficient sunt dependente de temperatura si mai ales de natura
gazului care este supus transformarii izobare.
Transformarea izoterma. Transformarea
izoterma este caracterizata prin mentinerea temperaturii
constante in timpul modificarii parametrilor de stare. Deoarece T =
constant, deci dT = 0 din 2.3 se obtine 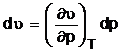 . Prin impartirea variatiei de volum la
volumul initial
. Prin impartirea variatiei de volum la
volumul initial ![]() 0, corespunzator temperaturii T0 rezulta
coeficientul
0, corespunzator temperaturii T0 rezulta
coeficientul 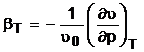 (2.5) care se denumeste coeficient de
compresibilitate izoterma. Semnul minus este introdus deoarece
variatia volumului cu presiunea este negativa - cresterea
presiunii conduce la scaderea volumului - iar coeficientul bT
trebuie sa fie pozitiv.
(2.5) care se denumeste coeficient de
compresibilitate izoterma. Semnul minus este introdus deoarece
variatia volumului cu presiunea este negativa - cresterea
presiunii conduce la scaderea volumului - iar coeficientul bT
trebuie sa fie pozitiv.
Intre
cei trei coeficienti exista relatia ![]() .
.
Energia.
Energia unnui corp sau a unui
sistem de corpuri este definita prin capacitatea acestora de a efectua un
lucru mecanic prin modificarea starii lor. Dupa natura
transformarii de la o stare la alta energia poate fi mecanica,
termica, electrica, hidraulica etc. a caror suma
reprezinta energia totala a corpului considerat. Pentru un sistem
termodinamic energia totala Et este suma dintre energia Ec
- energia cinetica, Ep - anergia potentiala si U
- energia interna. Se poate scrie expresia ![]() .
.
Energia cinetica - Ec - este o parte din energia totala care depinde exclusiv de marimile ce caracterizeaza starea sistemelor de miscare.
Energia potentiala - Ep - este energia pe care o are un sistem de particule, un corp, datorita pozitiei acestora fata de o configuratie de referinta - de exemplu in campul fortelor gravitationale.
Energia interna - U - potential termodinaic exprimat in functie de variabilele de stare. Este o marime de stare calorica cu valori bine determnata la fiecare stare termodinamica pe care o poate avea sistemul.
Legea conservarii energiei exprima ca intr-un sistem de corpuri care formeaza un tot izolat energia totala - suma tuturor formelor de energie - ramane constanta oricare ar fi natura modificarilor de stare care intervin in sistemul considerat. Pentru studiul proprietatilor unui corp sau sistem este comod sa se izoleze acesta de celelalte corpuri sau sisteme, denumite generic drept mediu exterior. Legea conservarii energiei devine: in cursul trecerii unui corp dintr-o stare in alta intervine un schimb de energie intre acesta si mediul exterior astfel incat suma energiilor corpului si mediului exterior ramane constanta.
Se
defineste drept caldura scimbul de energie dintre un corp
si mediul exterior care se manifesta prin modificarea starii
termice a corpului considerat ceea ce corespunde, in general, incalzirii
sau racirii acestuia. Matematic schiimbul de energie dintre un corp
si mediul exterior, in urma trecerii dintr-o stare (1) in alta (2), se
exprima prin diferenta ![]() dintre valorile
energiei corpului in cele doua stari.
dintre valorile
energiei corpului in cele doua stari.
Obiectul termodinamicii il constituie stabilirea relatiilor cantitative si calitative dintre caldura si lucru mecanic va urmare a schimbului de energie.
Lucrul mecanic - este reprezentatprintr-o schimbare a formei de miscare, analizata din punct de vedere cantitativ, proces in decursul careia o anumita forma de miscare trece in alta forma de miscare.
Pentru
o miscare de translatie lucrul mecanic este produsul dintre
forta aplicata unui corp F si deplasarea acestuia l sub actiunea
acestei forte: L = Fl. In
cazul unei particule care se deplaseaza pe o traiectorie curbilinie intre
punctele A ,i B lucrul mecanic este dat de integrala curbilinie ![]() , unde
, unde ![]() este lucrul mecanic
elementar reprezentat prin produsul scalr al fortei
este lucrul mecanic
elementar reprezentat prin produsul scalr al fortei ![]() si
deplasarii elementare
si
deplasarii elementare ![]() a punctului de
aplicatie a fortei F.
a punctului de
aplicatie a fortei F.
Forta
![]() genereaza pe o
suprafata a o presiune data de p = F/A si deci F = pA. Se introduce
expresia in lucrul mecanic elementar
genereaza pe o
suprafata a o presiune data de p = F/A si deci F = pA. Se introduce
expresia in lucrul mecanic elementar ![]() , dV fiind o variatie a volumului elementar. Ca urmare
lucrul mecanic este
, dV fiind o variatie a volumului elementar. Ca urmare
lucrul mecanic este ![]() .
.
|
1 dL L12 p 2 V 1 dV 2 Fig. 1. Definirea lucrului mecanic |
Lucrul mecanic de dislocare - de deplasare izobara a unui fluid. Notiunea respectiva este utilizata la sisteme deschise prin care se deplaseaza un fluid si este necesar deplasarii unei mase de fluid dintr-o parte a sistemului in alta (de exemplu conducte). Ca urmare Ld = pV fiind un lucru mecanic primit de masa de fluid din spate si cedat pentru deplasarea fluidului din fata.
Lucrul mecanic absolut - total. Intr-o
transformare de stare se realizeaza o deplasare oarecare de
substanta. Se cauta sa se determine lucrul mecanic care
sa descrie intreg procesul fiind consumat sau cedat de catre gaz. Se
considera un proces care evolueaza intre punctele 1 si 2 pe
diagrama din figura 1 in coordonate p si V. Se ia un volum elementar dV la
care se poate considera ca presiunea este constanta, deoarece dV este
foarte mic. Se obtine lucrul mecanic absolut 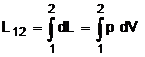 . Ca urmare, in conformitate cu definitia integralei
definite marimea ariei de sub curba reprezinta lucrul mecnaic
corespunzator transformarii.
. Ca urmare, in conformitate cu definitia integralei
definite marimea ariei de sub curba reprezinta lucrul mecnaic
corespunzator transformarii.
Conventional se considera lucrul mecanic produs de o masina ca fiind pozitiv, iar cel consumat sau primit ca negativ.
Terminologie.
Transformare termodinamica - trecerea unui sistem de la o stare de echilibru la alta; caracteristic este factorul timp.
Transformarea in cursul careia apare o crestere a volumului se numeste destindere, iar cea in care are loc o reducere a volumului se numeste compresiune.
Transformarea caracterizata prin mentinerea constanta a volumului este transformarea izocora.
Transformarea care apare prin mentinerea constanta a presiunii este denumita izobara.
Transformarea caracterizata de mentinerea constanta a temperaturii este transformarea izoterma.
Transformarile care apar intr-o incinta cu invelis de izolare termica ce nu permite schimb de energie termica cu exteriorul este transformarea adiabata la care apar modificari simultane ale celor trei parametri.
Caldura
Caldura
reprezinta schimbul de energie cu mediul datorat nivelului termic diferit
al sistemulu si mediului. Caldura si lucrul mecaniic sunt
marimi de proces sau marimi de transformare astfel incat din punct de
vedere matematic nu admit diferentiale totale exacte. Schimbul de
caldura este dat de relatia ![]() in care [Q] = J -
Joule, iar 1 kcal = 4,1868 kJ, unde c reprezinta caldura
specifica a procesului considerat pentru agentul de lucru intre
temperaturile de desfasurare ale procesului.
in care [Q] = J -
Joule, iar 1 kcal = 4,1868 kJ, unde c reprezinta caldura
specifica a procesului considerat pentru agentul de lucru intre
temperaturile de desfasurare ale procesului.
Pentru caldura, conventional, se adopta semnele: Q 0 in cazul in care o masina termica primeste caldura si Q 0 in procese de racire cand DT
Caldura specifica - cantitatea de caldura care se da unitatii de cantitate de substanta pentru a-si varia temperatura cu un grad. Caldura specifica depinde de: a) temperatura; b) natura transformarii la care este supus gazul in timpul procesului de incalzire sau racire; c) unitatea de cantitate de substanta; d) natura corpului.
Dependenta de presiune - pana la presiuni de 60 bari variatia caldurii specifice cu presiunea este redusa si deci, practic, se poate considera constanta.
Dependenta de natura transformarii. Se considera o cantitate de 1 kg de gaz perfect care se incalzeste de la T1 la T2 o data la volum constant si apoi la presiune constanta.
Volum constant. Prin incalzire de
la T1 la T2 se mareste agitatia
termica a moleculelor fapt care se traduce prin variatia energiei
interne; ca atare se considera caldura specifica la volum
constant cv si deci cantitatea de caldura este ![]() .
.
Presiune constanta. Gazul care se
incalzeste in acelasi ecart de temperatura ![]() se va dilata pentru a
mentine presiunea constanta - el va executa un lucru mecanic.
Asadar, este necesara o cantitate de caldura mai mare decat
in cazul precedent. Cantitatea de caldura se determina cu
expresia
se va dilata pentru a
mentine presiunea constanta - el va executa un lucru mecanic.
Asadar, este necesara o cantitate de caldura mai mare decat
in cazul precedent. Cantitatea de caldura se determina cu
expresia ![]() . Deoarece
. Deoarece ![]()
![]() rezulta ca cp
cv. Raportul celor doua marimi cp / cv
= k este denumit exponent adiabatic cu valori orientative: a) in cazul gazelor
monoatomice k = 1,66; b) gaze biatomice k = 1,4; c) gaze poliatomice k =
1,21,3.
rezulta ca cp
cv. Raportul celor doua marimi cp / cv
= k este denumit exponent adiabatic cu valori orientative: a) in cazul gazelor
monoatomice k = 1,66; b) gaze biatomice k = 1,4; c) gaze poliatomice k =
1,21,3.
Caldura specifica depinde de natura gazului prin numarul de atomi din molecula, starea in care se afla gazul, modul de obtinere a gazului si puritatea lui.
Principiile termodinamicii
|
I II III Fig. 2. Primul principiu al termodinamicii |
Principiul zero. Cronologic acest principiu a fost formulat mult mai tarziu dupa ce a fot cunoscute celelalte doua principii 1si 2. Doua sisteme in echilibru termic, considerate pe rand cu un al treilea sistem se afla, simultan, in echilibru termic unul cu altul.
Principiul zero subliniaza faptul ca temperatura este o marime caracteristica a echilibrului termic a corpurilor. Temperatura este o marime intensiva pentru fiecare stare a echilibru a sistemelor. Asadar, toate sistemele care se afla in echilibru termic au aceiasi temperatura si invers - sistemele care nu sunt in schilibru termic unele cu altele vor avea temperaturi diferite. Temperatura este omasura a incalzirii corpurilor si se stabileste totdeauna directia naturala de transmitere a caldurii intre corpuri.
Principiul unu al termodinamicii sau principiul echivalentei energiilor - echivalenta caldurii cu lucrul mecanic.. Primul principiu al termodinamicii reprezinta legea conservarii energiei aplicata la fenomenele care comporta schimburi de energie. In cazul unui sistem termodinamic izolat in care apar numai lucru mecanic si schimburile de caldura primul principiu al termodinamicii arata ca intre acestea exista o perfecta egalitate astfel ca unei anumite cantitati de caldura ii corespunde totdeauna acelasi lucru mecanic. Suma energiilor unui sistem termodinamic izolat este constanta oricare ar fi procesele care se desfasoara in afara sistemului.
Expresia matematica a primului principiu al termodinamcii este Q = AL, unde Q reprezinta schimburile de caldura, L - lucrul mecanic, A este echivalentul mecanic al kcal; relatia este valabila daca [Q] = kcal, [L] = kgfm, A = 1/427 [kcal/kgfm]. In sistemul international in care toate formele de energie se exprima in unitatea de masura Joule relatia se scrie direct sub forma Q = L [J].
Clasius a formulat ca: o masina termica nu poate produce continuu lucru mecanic fara a consuma o cantitate de caldura echivalenta din exterior.
Ostwald a formulat ca: perpetuum mobile de speta intai nu este posibil.
Energia interna si entalpia
Exista trei forme de energie Epot - potentiala, Ecin - cinetica, U - energia interna. Avand in vedere caracterul ei aditiv rezulta ca energia totala E este suma E = Epot + Ecin + U in care Epot este datorata interactiunii dintre sistem si mediul exterior ca urmare a pozitiei sistemului intr-un camp de forte exterioare (forte masice exterioare sistemului - de exemplu campul fortelor masice gravitationale, centrifugale etc.), Ecin - se datoreste starii de miscare a corpului ca un tot unitar si intr-o parte care nu depinde de conditiile exterioare, ci numai de cele interioareale sistemului considerat.
In
cazul unei transformari deschise se poate scrie expresia ![]() .
.
In
starea de repaus a corpului considerat in sistemul de forte - sau cand nu
se tine seama de miscare, caz concret in termodinamica -
relatia de mai sus se reduce la ![]() ; asadar, se poate scrie U2 - U1 =
Q12 - AL12. Termenul Q12 - AL12 sau
cel exprimat in sistemul international Q12 - L12 nu
depinde de natura transformarii respective, ci numai de starile
initiala si finala; energia interna este asadar
un parametru de stare derivat care este folosita la caracterizarea unei
stari de echilibru.
; asadar, se poate scrie U2 - U1 =
Q12 - AL12. Termenul Q12 - AL12 sau
cel exprimat in sistemul international Q12 - L12 nu
depinde de natura transformarii respective, ci numai de starile
initiala si finala; energia interna este asadar
un parametru de stare derivat care este folosita la caracterizarea unei
stari de echilibru.
Energia interna a unui corp omogen se descompune in energia potentiala Upot - datorata actiunii reciproce a particulelor elementare, energia cinetica Ucin - datorata miscarii termice a particulelor la care se adauga energia de zero U0; asadar, se poate scrie U = Upot + Ucin + U0.
Pentru studiul sistemelor termodinamice si a functionarii masinilor termice se dovedeste utila definirea functiei H = U + pV denumita entalpia termodinamica sau pe scurt entalpia sistemului J. Entalpia este un parametru derivat.
In caz general variatia entalpiei este DH = DU + D(pV), iar pentru o transformare oarecare deschisa variatia entalpiei este DH =(U2 + p2V2) - (U1 + p1V1) = H2 - H1.
Pentru o masa unitara, m = 1 kg, de gaz perfect se defineste entalpia specifica h = u + pn [J/kg].
Entalpia fiind o marime calorica de stare va admite diferentiala totala exacta si se constata ca este functie de temperatura H = H(T).
Entalpia ia in considerare energia interna U si lucrul mecanic de dislocare pV. Ca urmare la trecerea unui sistem dintr-o stare in alta variatia entalpiei va tine cont de variatia energiei interne DH cat si de diferenta lucrurilor mecanice de dislocare in cele doua stari D(pV).
Ecuatia caracteristica
Intr-un sistem termodinamic intervin mai multe marimi: G - greutatea gazului, p - presiunea, V - volumul, T - temperatura. Variatia unei marimi oarecare, la trecerea sistemului de la o stare la alta, va atrage modificarea celorlalte. Ca urmare exista o lege care leaga toti acesti parametri sub forma functiei f(G, p, V, T) = 0 ce poate caracteriza univoc sistemul termodinamic denumita ecuatia caracteristica a sistemului.
In cazul sistemelor termodinamice omogene (simple) marimea G este corelata cu volumul V prin relatia G = g V si ca uramre se poate reduce functia de mai sus la f(p, V, T) = 0.
Ecuatiile caracteristice exprima particularitatile individuale ale sistemului considerat.
Reprezentarea grafica a expresiei de mai sus conduce la o suprafata in spatiu - de evolutie a starilor sistemului.
Expresiile matematice ale primului principiu al termodinamicii
|
2 p2, V2, T2 p1, V1, T1 1 L12 w1 w2 z2 z1 Fig. 3. Sistem deschis |
Sisteme deschise. Sistemul descris este acela care schimba energie cu mediul exterior sub forma de caldura si lucru mecanic si prin care se deplaseaza o cantitate de substanta.
Se
considera un sistem deschis prin care trece o cantitate de
substanta. In sistem se schimba o cantitate de caldura
Q12 si lucru mecanic L12, figura . In sectiunea
de intrare agentul de lucru are parametrii p1, V1, T1
si viteza w1 cu energia E1, iar la iesire in
punctul 2 are p2, V2, T2 respectiv viteza w2
si energia E2. Bilantul energetic arata ca E2
- E1 = aEs - suma energiilor schimbate cu
mediul exterior in care acestea au expresiile ![]() si
si ![]() Termenul
aEs
reprezinta caldura primita si cedata prin
interactiunile agentului de lucru cu exteriorul de forma aEs = Q12
- L12 + (p1V1 - p2V2).
Asadar, ecuatia de bilant energetic este
Termenul
aEs
reprezinta caldura primita si cedata prin
interactiunile agentului de lucru cu exteriorul de forma aEs = Q12
- L12 + (p1V1 - p2V2).
Asadar, ecuatia de bilant energetic este
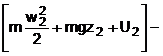
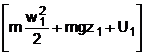 = Q12 - L12 +
(p1V1 - p2V2)
= Q12 - L12 +
(p1V1 - p2V2)
sau daca se pune sub alta forma din punct de vedere matematic rezulta
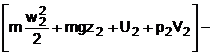
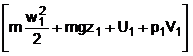 = Q12 - L12.
= Q12 - L12.
Deoarece termenii de
entalpie sunt dati de H = U + pV rezulta H1 = U1
+ p1V1 si respectiv H2 = U2 +
p2V2. Ca urmare ecuatia energiei devine 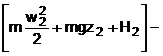
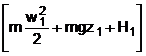 = Q12 - L12 sau
pusa sub alta forma
= Q12 - L12 sau
pusa sub alta forma ![]() care constituie expresia
matematica a primului principiu a termodinamicii pentru sistemele
deschise.
care constituie expresia
matematica a primului principiu a termodinamicii pentru sistemele
deschise.
Sisteme inchise. Este cazul acelor sisteme la care agentul de lucru nu face schimb de energie si masa cu mediul exterior - agentul de lucru ramane inchis si masina - sau se schimba - cazul unui cilindru cu piston care inchide o cantitate de gaz. Din ecuatia energiei de mai sus dispare primul termen deoarece w1 = w2 ( nu apare proces de curgere) si cotele z1 = z2. Ca urmare se obtine H2 -H1 = Q12 - L12 sau Q12 = H2 - H1 + L12. Deoarece H = U + pV rezulta expresia Q12 = (U2 + p2V2) - (U1 + p1V1).
Transformari simple de stare, reversibile
Pentru studiul proceselor care se desfasoara in masinile termice se impun anumite ipoteze care conduc la studiul a cinci transformari de stare:
transformarea izocora p = constant, legea Gay-Lussac;
transformarea izocora u = constant, legea Charles;
transformarea izoterma T = constant, legea Boyle-Mariotte;
transformarea adiabata;
transformarea politropa - transfomarea in care variaza concomitent toti parametri de stare si se regasesc toate formele de energie.
Transformarile sunt reversibile daca se pot produce in ambele sensuri; sistemul trece, in ambele cazuri prin aceleasi stari intermediare, cu aceleasi conditii exterioare.
Transformarea izobara.
|
2 p2 = p1 V2, T2 p1, V1, T1 Fig. 4. Schema transformarii la presiune constanta |
Transformarea se petrece la presiune constanta, p = constant, astfel incat intre ceilalti doi parametri se stabileste corelatia u/T = constant, sau deoarece u r rezulta rT = constant - legea Gay - Lussac.
Conditiile in care se realizeaza o transformare izobara sunt mentionate mai jos. Se considera un cilindru care se incalzeste si in care s epoate deplasa un piston, figura 4. In cillindru se introduce un kilogram de gaz perfect si apoi se incalzeste cilindrul. Prin incalzire creste temperatura gazului care se dilata, expandeaza si pentru a mentine presiunea constanta se deplaseaza pistonul de la pozitia 1 la cota 2 astfel incat p1 = p2 = p = constant.
|
1 p1 = p2 2 L12 u u u Fig. 5. Diagrama transformarii izobare |
Transfomarea izobara este caracteristica proceselor de ardere in care o masina primeste caldura pentru efectuarea unui lucru mecanic sau cedeaza caldura in procesele de racire. Prezentarea grafica a transformarii izobare este data in figura 5 in coordonate p u
Lucrul
mecanic absorbit este dat de integrala lucrului
elementar dL = p du si deci se obtine 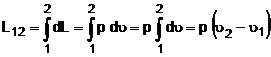 [J].
[J].
Se face observatia ca masinile termice nu pot lucra in conditii izobare, ci numai pe baz unei transformarii care implica o variatie a presiunii.
Schimbul de caldura cu mediul exterior este Q12 = m Cp (t2 - t1 [J] egal cu variatia entalpiei. Cantitatea de caldura primita in timpul acestei transformari se foloseste atat pentru variatia energiei interne cat si pentru efectuarea unui lucru mecanic necesar mentinerii constante a presiunii.
Transformarea izocora
|
V1 = V2 Fig. 6. Schema transformarii izocore |
Aceasta
transformare se caracterizeaza prin mentinerea
Transformarea izocora este caracteristica proceselor de ardere la valoare constanta si proceselor de racire. Cantitatea de caldura este Q = m Cv (t2 - t1) [J].
|
Fig. 7. Diagrama transformarii izocore |
Lucrul
mecanic elementar este dL = p dV si deci se obtine 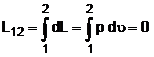 , conform figurii 7. Transformarea izocora se realizeaza fara
efectuare de lucru mecanic.
, conform figurii 7. Transformarea izocora se realizeaza fara
efectuare de lucru mecanic.
In cazul transformarii izocore schimbul de caldura cu mediul este egal cu variatia energiei interne. Caldura primita de gaz este folosita doar pentru variatia energiei interne. Transformarea produsa in sensul cresterii presiunii, deci a temperaturii Dp > 0 reprezinta o incalzireLt < 0 - lucrul mecanic tehnic. Transformarea ce apare prin reducerea presiunii corespunde scaderii temperaturii - proces de racire Dp < 0.
Transformarea izocora apare atunci cand se incalzeste un gaz cuprins intr-o incinta inchisa.
Transformare izoterma.
|
p2, V2 p1, V1, T1 Fig.8. Schema cilindrului in transformarea izoterma |
Transformarea izocora este acea transformare caracterizata prin mentinerea temperaturii constante in cursul evolutiei gazului din incinta, T = constant. Ecuatia de stare este T(p, V) = constant.
Se considera un cilindru in care se deplaseaza un piston, figura 8. Pentru mentinerea constanta a temperaturii cilindrul este prevazut cu un sistem de termostatare care sa preia sau sa dea caldura, primita respectiv cedata, in timpul variatiei presiiunii. In masinile termice mentinerea constanta a temperaturii este un deziderat ce nu poate fi tehnic realizat.
Legea transformarii izoterme este pV = constant, p1V1 = p2V2 = = pV= constant. Ca urmare se obtine legea pV = mRT, reprezentata grafic in figura 9.
|
p1 1 L12 2 P2 V1 V2 Fig. 9. Schema transformarii izoterme |
Lucrul
mecanic se determina din integrala lucrului mecanic elementar dL = p dV.
Se obtine 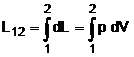 . Din expresia transformarii izoterme p1V1 = pV
rezulta legea de variatie a presiunii p = p1 V1/V
care se inlocuieste in integrala si se obtine
. Din expresia transformarii izoterme p1V1 = pV
rezulta legea de variatie a presiunii p = p1 V1/V
care se inlocuieste in integrala si se obtine 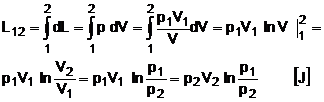
Grafic transformarea izoterma este o hiperbola echilatera pV = constant, figura 9. Lucrul mecanic este dat de aria hasurata de sub curba din figura 9. Cand transformarea se efectueaza in sensul cresterii volumelor DV > 0 se produce lucru mecanic L > 0 - proces de destindere. Cand transformarea se face in sensul reducerii volumului DV < 0 se obtine L < 0 se absoarbe lucru mecanic - proces de comprimare. In transformarea izoterma a unui gaz perfect schimbul de caldura se regaseste integral in lucru mecanic.
Energia interna - variatia ei este data de dU = m cv dT = 0 - nu apare variatie a energiei interne si nu se realizeaza variatia entalpiei.
Transformarea adiabata.
Prin definitie transformarea adiabata a unui gaz perfect are loc intr-o incinta cu invelis adiabatic care nu permite schimb de caldura cu mediul exterior si in care variaza toti parametrii de stare p, V, T. Transformarea adiabata poate fi reversibila sau ireversibila. O transformare adiabata ireversibila este destinderea unui gaz, in vid, intr-o incinta izolata, din punct de vedere termic; in acest caz lucrul mecanic este nul si deci U = constant. Daca gazul este suficient de rarefiat atunci el se comporta ca un gaz perfect - experienta Gay-Lussac.
|
starea 2 p2, V2, T2 izoterma 1 adiabata V T 1 L12 2 V Fig. 10. Suprafata caracteristica, sistemul incinta si piston, diagrama de functionare in coordonate p, V. |
In spatiul p, V, T apare o suprafata caracteristica si prin intersectia cu diverse plane rezulta curbele caracteristice.
In
coordonate p,V se obtine o curba similara cu cea a izotermei
(figura 9), dar amplasata sub aceasta curba. Suprafata
caracteristica hasurata din diagrama de functionare
reprezinta lucrul mecanic L12. Din diagrama rezulta
ca adiabata are o panta mai mare decat cea corespunzatoare
transformarii izoterme, deci curba caracteristica este tot o
hiperbola cu un coeficient k superior. Daca in transformarea
izoterma este valabila legea pV = constant, pentru transformarea adiabata
apare legea pVk = constant sau p/rk
= constant. In coordonate p, T este valabila legea ![]() = constant.
= constant.
Lucrul
mecanic este dat de integrala 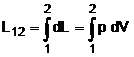 . Pentru a efectua integrala se scrie legea adiabatei sub forma
. Pentru a efectua integrala se scrie legea adiabatei sub forma ![]() din care rezulta expresia
presiunii
din care rezulta expresia
presiunii 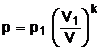 care se introduce in integrala.
Rezulta expresia lucrului mecanic de forma
care se introduce in integrala.
Rezulta expresia lucrului mecanic de forma 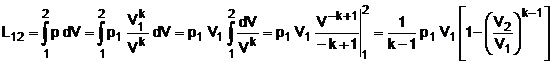
Din
legea de variatie a transformarii rezulta ![]() din care se obtine raportul
volumelor
din care se obtine raportul
volumelor 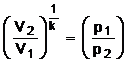 din care se obtine
din care se obtine 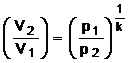 sau
sau 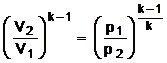 care se inlocuieste in expresia
lucrului mecanic. Rezulta, asadar expresia lucrului mecanic de forma
care se inlocuieste in expresia
lucrului mecanic. Rezulta, asadar expresia lucrului mecanic de forma 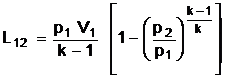
In transformarea adiabata lucrul mecanic este L12 = U1 - U2 si ca urmare in cazul unei destinderi adiabate lucrul mecanic se realizeaza in detrimentul energiei interne a gazului care evolueaza. In cazul comprimarii gazului energia interna a gazului va creste. Se poate da astfel o noua formulare a primului principiu al termodinamicii: la trecerea unui sistem termodinamic dintr-o stare in alta in conditii adiabate lucrul mecanic depinde numai de starile initiala si finala.
Transformarea politropa.
Similar transformarilor izoterma si adiabata si in acest caz variaza toate marimile de stare simultan p, V, T. Se numeste transformarea politropa transformarea in cursul careia capacitatea calorica - respectiv caldura specifica a sistemului - ramane nemodificata. In sistemul triortogonal se obtine o suprafata a carei puncte sunt determinate de valorile p, V, T. Prin sectionare cu plane paralele planelor de coordonate se obtin legile:
In coordonate p, V rezulta p Vn = constant;
In
coordonate T, V se tine cont de legea fundamentala pV = mRT sau ![]() sau
sau ![]() constant din care rezulta
constant din care rezulta ![]() constant;
constant;
|
izoterma
L12 politropa 1 2 V Fig. 11. Reprezentarea transformarii politrope |
In
coordonate p,T din legea fundamentala
rezulta 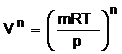 din care se obtine p Vn = constant, din care
din care se obtine p Vn = constant, din care 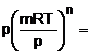 constant sau
constant sau ![]() constant ce poate fi scrisa sub forma
constant ce poate fi scrisa sub forma 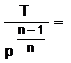 constant, in care n este exponentul politropic.
constant, in care n este exponentul politropic.
Lucrul
mecanic rezulta din integrala 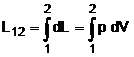 reprezentat de aria de sub
curba hasurata in figura 11. Prin integrare se obtine o
expresie similara celei calculata pentru transformarea adiabatei
reprezentat de aria de sub
curba hasurata in figura 11. Prin integrare se obtine o
expresie similara celei calculata pentru transformarea adiabatei 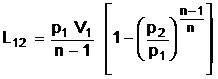 sau daca se tine cont de
legea generala a gazelor perfecte p V = m R T se obtine expresia
sau daca se tine cont de
legea generala a gazelor perfecte p V = m R T se obtine expresia 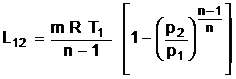
Transformarea politropa se reprezinta in planul p,V prin hiperbola p Vn = constant care se amplaseaza sub curba izotropei si deasupra adiabatei, deoarece 1 < n < k.
Valoarea
exponentului politropic n variaza in cursul transformarii politropice
si el depinde de natura gazului. In diagrama politropa se
situeaza intre izoterma si adiabata care pleaca din acelasi
punct 1, figura 11. Exponentul politropic este dat de expresia ![]() sau
sau ![]() , in care Cn este caldura specifica din transformarea
politropica, cu 1 < n < k.
, in care Cn este caldura specifica din transformarea
politropica, cu 1 < n < k.
|
izoterma izoterma adiabata politropa a adiabata b V V Fig. 12. Transformarile simple pentru procesul de destindere (a) si comprimare (b) |
Transformarile simple sunt cazuri particulare ale politropei: a) izobara Cn = Cp; b) izocora Cn = Cv; c) izoterma Cn , cu n = 1; d) adiabata Cn = 0 pentru n = k.
Masini si instalatii termice
Instalatiile termice se impart in doua categorii: Instalatii de forta si instalatii de lucru. O instalatie termica este un ansamblu de elemente mecanice cu miscari relative intre ele care realizeaza conversia energiei termice in energia mecanica.
Instalatiile termice de forta produc lucru mecanic prin arderea unui combustibil. Aceste instalatii desemneaza motoarele cu ardere interna, turbinele cu gaze, motoarele cu reactie si instalatiile de forta cu abur.
Masinile termice de lucru sunt acele mecanisme care utilizeaza o energie mecanica, electrica etc. pentru a mari capacitatea de lucru a unui gaz. Exemplele sunt: compresoarele, suflantele, turbosuflantele, turbocompresoarele, ejectoarele etc.
Compresoare
Masinile de lucru care transforma energia mecanica de la arbore in energie a unui gaz comprimat. Compresoarele pot fi construite sub forma unor masini cu piston, masini rotative sau de tip turbomasini.
|
4 3 izoterma
adiabata 1 2 p1 PMS PMI V Vc Fig. 13. Diagrama de lucru a unui compresor cu piston p1 - presiune de aspiratie p2 - presiune de refulare Vc - volumul cilindrului 1-2 - aspiratie la presiune constanta 2-3 - faza de comprimare 3-4 -refulare la presiune constanta 4-1 - faza fictiva de destindere |
Compresoarele cu piston pot realiza presiuni la cerere, masina se poate adapta la orice cerere a instalatiei pe care o deserveste. Astfel, ele pot asigura presiuni de 1000 bari la debite de 450 m3/min.
Diagrama de functionare este data in figura 13. Ipotezele de lucru sunt:
a) pistonul etanseaza perfect in cilindru fapt care nu permite pierderi de gaz pe langa organele de etansare (in special segmenti);
b) b) pistonul se lipeste perfect de capacul cilindrului fara a lasa un spatiu mort;
c) presiunea din colectoarele de admisie si refulare se pastreaza constanta in tot timpul efectuarii unui ciclu complet - timpul necesar trasarii unei diagrame indicate ca in figura 13;
d) in cilindrul compresorului evolueaza un gaz perfect care nu schimba faza in timpul efectuarii unei diagrame, a unui ciclu cmplet;
e) in fazele de aspiratie si refulare se admite ca parametrii gazlui nu se schimba.
Pentru calculul compresorului cu piston se defineste raportul de comprimare q = p2/p1 prin raportul presiunilor de refulare respectiv aspiratie. Intr-o singura treapta raportul de comprimare este limitat din considerente constructive, deoarece compresorul intr-o treapta poate realiza o presiune de p2 = 510 bari.
Lucrul mecanic este reprezentat
de spatiul interior cuprins in interiorul diagramei trasate, 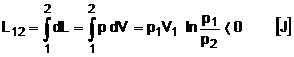 , calculat cu formula lucrului mecanic in ipoteza unei transformari
izoterme; este un lucru mecanic consumat, deci el trebuie furnizat din
exteriorul masinii de la un grup de antrenare.
, calculat cu formula lucrului mecanic in ipoteza unei transformari
izoterme; este un lucru mecanic consumat, deci el trebuie furnizat din
exteriorul masinii de la un grup de antrenare.
Deoarece singura posibilitate reala de functionare este in trasfomare pollitropa rezulta ca trebuie adoptate masuri tehnice, practice, pentru reducerea exponentului politrop in sensul apropierii de valoarea 1 - valoare caracteristica izotermei. Totodata se mentioneaza ca prin comprimarea gazului se produce o ridicare a temperaturii acestuia care nu trebuie sa atinga valoarea de autoaprindere a uleiului de ungere; in caz contrar se produce explozia masinii si distrugerea acesteia - compresorul se transforma intr-un motor cu autoaprindere prin comprimare de tip Diesel.
|
4 3 p2 C B p1 D A V Va Vc Fig. 14. Diagrama indicata a compresorului cu piston |
Compresorul tehnic cu piston mentine un volum mort necesar inchiderii si deschiderii supapelor, dilatarii reperelor, acoperirii abaterilor ale tolerantelor de executie etc. fapt care face ca pistonul sa nu se lipeasca de capacul cilindrului. In punctul 4, din diagrama data in figura 14, se inchide SR supapa de refulare si ramane o cantitate de gaz la presiune ridicata care se destinde ca urmare a miscarii pistonului. Nu toata cursa pistonului este utilizata pentru aspiratie; o parte din ea este folosita pentru necesitati functiionale de reluare a procesului. Intre punctele 1, 2 se realizeaza aspiratia in cilindru ca urmare a deschiderii supapei de aspiratie in punctul 1. Prin inchiderea acestei supape, in punctul 2, si deplasarea pistonului de la punctul mort exterior la cel interior se realizeaza compresia gazului aspirat. In punctul 3 datorita presiunii ridicate se deschide supapa de refulare, in mod automat, si se refuleaza gazul in conducta de refulate.
Puterea
consumata de compresor este puterea utila data de expresia 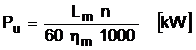 , unde Lm este lucrul mecanic consumat de
compresorul teoretic [J/diagrama], n - turatia arborelui masinii
[rot/min], hm - randamentul mecanic al compresorului
care ia in considerare toate pierderile mecanice prin frecarea pistonului in
cilindru, supape, lagare etc. cu hm
, unde Lm este lucrul mecanic consumat de
compresorul teoretic [J/diagrama], n - turatia arborelui masinii
[rot/min], hm - randamentul mecanic al compresorului
care ia in considerare toate pierderile mecanice prin frecarea pistonului in
cilindru, supape, lagare etc. cu hm
Puterea
motorului electric de antrenare a compresorului este ![]() , unde htr este randamentul
transmisiei de la motorul electric la compresor cu htr > 0,9, iar k = 1,11,2 coeficient de rezerva de putere.
, unde htr este randamentul
transmisiei de la motorul electric la compresor cu htr > 0,9, iar k = 1,11,2 coeficient de rezerva de putere.
Debitul compresorului. Debitul aspirat
in compresorul ideal este dat de expresia ![]() [m3/s],
unde D estediametrul pistonului - cilindrului, c - cursa pistonului ( c = 2r -
cursa pistonului este dublul razei butonului manivelei), n - turatia
arborelui compresorului, i - numarul de cilindri ai compresorului. Debitul
real este
[m3/s],
unde D estediametrul pistonului - cilindrului, c - cursa pistonului ( c = 2r -
cursa pistonului este dublul razei butonului manivelei), n - turatia
arborelui compresorului, i - numarul de cilindri ai compresorului. Debitul
real este ![]() , in care hv este randamentul volumic
care ia in considerare pierderile de debit datorita neumplerii complete
si corecte a cilindrului compresorului, precum si pierderile datorate
incalzirii gazului in urma procesului de comprimare.
, in care hv este randamentul volumic
care ia in considerare pierderile de debit datorita neumplerii complete
si corecte a cilindrului compresorului, precum si pierderile datorate
incalzirii gazului in urma procesului de comprimare.
Deoarece un compresor cu piston are un raport de comprimare limitat, pentru obtinerea unor presiuni ridicate este necesar sa se fractioneze raportul de presiuni in mai multe trepte. Apar astfel compresoarele cu mai multe trepte de comprimare cu cilindrii dispusi in serie prin care gazul trece succesiv. Pentru a realiza conditiile de ungere si a mari gradul de umplere intre trepte gazul se poate raci in schimbatoare de caldura exterioare prin care trece gazul comprimat intre etajele compresorului.
Motoare termice cu ardere interna
Acestea sunt masini termice in interiorul carora arderea unui gaz combustibil conduce la obtinerea unei cantitati de caldura cu realizarea unui lucru mecanic util la arborele masinii. Pentru studiul unei astfel de masini se utilizeaza ipotezele urmatoare:
Dupa modul in care se realizeaza procesul de ardere a combustibilului motoarele cu ardere interna se clasifica in:
cu ardere la volum constant - se aspira un amestec format din aer si vapori de combustibili care dupa comprimare se aprinde prin declansarea unei scantei electrice MAS - motoare cu aprindere prin scanteie;
cu ardere la presiune constanta - se aspira aer care se comprima si la sfarsitul comprimarii se injecteaza combustibil care se autoaprinde datorita faptului ca aerul comprimat are o temperatura inalta peste cea de aprindere a combustibilului - MAC - motor cu aprindere prin comprimare.
Dupa numarul de curse simple ale pistonului motoarele pot fi: a) motor in doi timpi - un ciclu de functionare se realizeaza la doua curse simple; b) motor in patru timpi - un ciclu de ardere se realizeaza la patru curse simple ale pistonului.
Motorul cu ardere la volum constant in patru timpi - MAS - motorul OTTO
|
3 ardere 2 Destindere scanteie Lc comprimare 4 0 aspiratie 1 evacuare V PMS Vs PMI Vc Fig. 15. Diagrama motorului termic cu aprindere prin scanteie |
Se definesc marimile:
Raport de comprimare - raportul dintre volumul cilindrului si volumul camerei de ardere e = Vc/V0 cu e < 10;
Raport de crestere a presiunilor - raportul dintre presiunea de la sfarsitul arderii si presiunea de la inceputul arderii l = p3/p2 cu l < 3,5;
Volumul cursei pistonului denumit si cilindree.
Functionare.
Pistonul se deplaseaza in cilindru de la PMS la PMI, intr-o miscare rectilinie alternativa, realizand admisia unui amestec format din aer si benzina. Introducerea vaporilor de benzina in aer se realizeaza prin aspiratie - in carburator - sau prin injectie - cu pompa si injectoare care pulverizeaza benzina la mare presiune. La cursa pistonului dintre PMI catre PMS se realizeaza comprimarea amestecului. Inainte de a ajunge la PMS - avansul la aprindere - se declanseaza o scanteie electrica, datorita unui sistem de inalta tensiune, care provoaca arderea combustibilului in amestec.Ca urmare a arderii se produce o crestere rapida a presiunii, practic la volum constant 2-3, si se degaja o mare cantitate de caldura. Gazele se destind intre 3-4 cand apare faza de destindere singura faza producatoare de lucru mecanic care conduce la impingerea pistonului in jos. Inainte de punctul 4 se deschide supapa de evacuare astfel ca, practic la volum constant, scade foarte repede presiunea; ca urmare 4-1 este o transformare izocora deoarece volumul scade foarte putin, dar presiunea variaza foarte mult intr-un interval foarte scurt de timp. Intre 1 si 0 se evacueaza gazele arse si la cursa inversa 0-1 se realizeaza admisia amestecului si se reia ciclul.
In principiu, motorul cu aprindere prin scanteie este similar constructiv cu pompa cu piston cu deosebirea ca in acest caz supapele sunt comandate prin sisteme de ax cu came si tacheti cu miscare corelata cu cea a pistonului (in cazul pompelor cu piston supapele au o miscare automata comandata prin diferenta de presiune de pe cele doa fete ale talerului).
Asadar,apar urmatoarele faze identificate pe diagrama din figura 15:
a) faza I 0 - 1 admisia amestecului de aer si benzina intr-o proportie care permite arderea in incinta inchisa formata din cilindru si piston; b) faza a II-a 1 - 2 comprimarea amestecului; c) faza a III-a 2 - 3 arderea amstecului aer-benzina cu aprinderea data de o scanteie comandata si corelata cu miscarea pistonului in cilindru; d) faza a IV-a 3 - 4 destinderea gazelor arse cu evacuarea caldurii in exteriorul incintei si deplasarea pistonului sub actiunea fortei de presiune; e) faza a V-a 4 - 1 evacuarea libera a gazelor arse datorita presiunii mari din cilindru superioara celei atmosferice in care se realizeaza refularea acestora; f) faza a VI-a 1 - 0 evacuarea fortata a gazelor arse datorita miscarii pistonului catre punctul mort superior.
In diagrama din figura 15 apar transformarile simple de izocora, izobara si adiabata. Ca urmare pentru fiecare dintre ele se aplica formulele stabilite la capitolul transformarilor simple. Astfel se pot stabili relatiile:
a) raport de comprimare ![]() din care rezulta
din care rezulta ![]() ;
;
b) transformarea
adiabata ![]() de unde se obtine expresia
presiunii
de unde se obtine expresia
presiunii 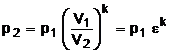
c) in transformarea izocora exista
expresia ![]() , dar
, dar ![]() din care presiunea in
punctul 3 este
din care presiunea in
punctul 3 este ![]() ;
;
d) transformarea
adiabata 3 - 4 conduce la valoarea presiunii in punctul 4 ![]() din care rezulta
din care rezulta 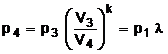 .
.
Motorul primeste caldura numai in faza de ardere 2 - 3 izocora stabilita prin relatia Q23 = m Cv (T3 - T2) [J/ciclu].
|
e Fig. 16. Variatia randamentului termic |
Cantitatea de
caldura pe care o primeste gazul pe un ciclu este 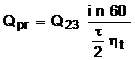 [kJ/ora], unde i
reprezinta numarul de cilindri ai motorului, Q23 -
cantitatea de caldura cedata prin arderea amestecului
combustibil pe un ciclu, t - numarul de timpi
ai motorului, ht randamentul transformarii
caldurii cu valori de peste 90%. Daca in formula de mai sus nu se
introduce randamentul de transformare a caldurii se obtine cantitatea
de caldura teoretica.
[kJ/ora], unde i
reprezinta numarul de cilindri ai motorului, Q23 -
cantitatea de caldura cedata prin arderea amestecului
combustibil pe un ciclu, t - numarul de timpi
ai motorului, ht randamentul transformarii
caldurii cu valori de peste 90%. Daca in formula de mai sus nu se
introduce randamentul de transformare a caldurii se obtine cantitatea
de caldura teoretica.
Elementele fundamentale ce caracterizeaza un motor termic sunt: a) cilindreea - volumul total de lucru al cilindrilor; b) forma camerei de ardere; c) raportul de comprimare; d) randamentul termic al arderii; e) consumul orar de combustibil; f) fiabilitatea si durabilitatea motorului termic.
Randamentul
termic al motorului este functie de raportul de comprimare e si de exponentul adiabat k, figura 16, conform expresiei ![]() .
.
Motorul cu ardere interna la presiune constanta MAC - Diesel
|
PMI C P PME B Fig. 17. Schema motorului de tip MAC SA - supapa de aspiratie SR - supapa de evacuare In - injector pulverizare PMI - punct mort interior PME - punct mort exterior C - cilindru P - piston B - biela |
Schema constructiei motorului in patru timpi, precum si functionarea este identica cu cea a motorului cu aprindere prin scanteie. Deosebirea intre cele doua motoare este in modul de umplere a cilindrului. La motorul Otto umplerea se realizeaza cu un amestec de aer-combustibil in timp ce la motorul Diesel se aspira aer curat care se comprima si se injecteaza apoi combustibilul pulvarizat la finele fazei de comprimare. Avantajul acestui tip de motor este ca se pot folosi hidocarburi grele, mai putin volatile: motorina, gudroane, uleiuri de parafina sau chiar pacura.
Motoarele MAC functioneaza cu rapoarte mari de compresie e = 1430 pentru a realiza prin comprimarea aerului curat, la finele fazei, temperaturile de 6307500 C care permit autoaprinderea combustibilului injectat in spatiul mort de deasupra pistonului.
Functionare.
|
2 Q 3 p2 = p3 Injectie In destindere comprimare evacuare 0 aspiratie 1 PMI PME V Vs V0 Vc Fig. 18. Diagrama de lucru a motorului cu aprindere prin comprimare |
In cursa pistonului de la PMI la PME, 0 - 1 in figura 18, se aspira aer curat in cilindru, faza in care supapa de aspiratie este deschisa. In aceasta etapa presiunea este cea atmosferica sau chiar putin mai mare decat aceasta la motoarele cu supraalimentare la care aerul este introdus fortat in cilindru cu ajutorul unei turbosuflante. La cursa inversa a pistonului, de la PME la PMI se comprima aerul, scade volumul si corespunzator se majoreaza presiunea si temperatura. Inainte ca pistonul sa ajunga in PMI, avansul corespunzator constructiei si turatiei motorului, se injecteaza in cilindru, la presiune mare, o cantitate precisa de combustibil. Avansul la aprindere, care se face si la motorul cu aprindere prin scanteie,trebuie sa compenseze durata de intarziere a frontului flacarii (2,02,5) 10-3 secunde in functie de gradul de turbulenta din spatiul de ardere. Datorita presiunii ridicate de injectie (1502000 bari) combustibilul este pulverizat foarte fin, ca o ceata, astfel incat se poate realiza un amestec bifazic omogen care poate arde usor si integral. Aprinderea amestecului se realizeaza automat ca urmare a temperaturii ridicate a aerul comprimat. Initierea arderii se face spre periferie (circa 10%) cand arderea are loc in conditii practic izocore provocad o crestere brusca a presiunii si temperaturii in spatiul de ardere. Acest surplus de energie de activare face ca restul combustibilului acumulat si injectat (circa 90%) sa arda practic instantaneu, fara intarziere la aprindere. In aceasta faza, cu pondere mult mai mare, presiunea creste foarte putin sau chiar scade putin fapt care justifica denumirea de motor cu ardere la presiune constanta.
Arderea se considera izobara intre punctele 2 si 3 si pistonul se deplaseaza pe o portiune dintre PMI si PME. In continuare gazele se destind - curba 3 -4 - destinderea se considera o transformare adiabata care constituie faza motoare a ciclului.
Inainte de punctul 4 se deschide supapa de evacuare permitand astfel scaderea presiunii din cilindru pana la valoarea presiunii de evacuare din sistemul de esapament. In ultima cursa a pistonului de la PME la PMI pistonul impinge gazele arse in exteriorul cilindrului. Dupa aceasta faza se reia ciclul celor patru timpi ai motorului.
Asadar, in motorul cu aprindere prin comprimare, apar mai multe faze:
Marimile caracteristice pentru motorul Diesel
Raport de comprimare
definit prin raportul volumelor ![]() ;
;
Coeficient sau grad de
injectie - raportul de crestere a volumelor in procesul de ardere
egal cu raportul dintre volumul la sfarsitul arderii si volumul
camerei de ardere ![]() .
.
Elementele de calcul ale motorului sunt precizate mai jos.
Pentru
adiabata 1-2 este valabila legea ![]() din care se poate obtine
expresia presiunii
din care se poate obtine
expresia presiunii 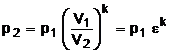 deoarece
deoarece ![]() .
.
Presiunea
in punctul p3 se determina in baza transformarii izobare
sub forma ![]() - valoarea presiunii
de la sfarsitul arderii.
- valoarea presiunii
de la sfarsitul arderii.
Gradul
de injectie definit mai sus conduce la volumul V3 conform
expresiei ![]() .
.
Pentru
izobara 2 - 3 la presiune constanta rezulta temperatura ![]() din care se
obtine
din care se
obtine ![]() cu V4 = V1.
cu V4 = V1.
In
cazul transformarii adiabate 3 - 4 se poate scrie ![]() din care rezulta
din care rezulta 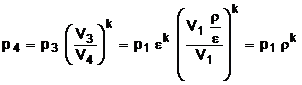 ; asadar
; asadar ![]()
|
3 4 ardere destindere 2 injectie 5 comprimare pr evacuare 0 1 pas admisie V V0 Vc Fig. 19. Ciclul mixt de ardere in motorul MAC |
Schimbul
de caldura cu mediul exterior este dat de
expresia bine cunoscuta Q = m Cp DT. Motorul primeste caldura
numai in faza de ardere izobara Q23 = m Cp (T3
- T2) = ![]() > 0
masurata in [Joule/ciclu].
> 0
masurata in [Joule/ciclu].
Lucrul mecanic se determina cu relatia L = L12 + L23 + L34 + L41 si este reprezentat prin aria hasurata din figura 18.
Pentru motorul cu aprindere prin comprimare se poate imagina, prin considerarea mecanismului arderii combustibilului, si un ciclu mixt cu arderi succesive in care prima este o izocora si a doua faza este izobara. In acest mod ciclul se apropie mai mult de realitatea functionarii motorului MAC.
In cazul diagramelor precizate pentru motoarele cu ardere interna se precizeaza ca presiunea de aspiratie este de regula (fara supraalimentare) pas = 0,9 patm, iar cea de evacuare pev = 1,1 patm. Randamentele termice ale motoarelor cu ardere interna sunt: a) motoare cu scanteie dotate cu carburator h .0,35; b) in cazul motoarelor cu gaze h = 0,28.0,33; c) pentru motoarele cu aprindere prin comprimare h
Turbine cu gaze
|
4 7 10 13 1 2 3 8 9 posibil 11 12 Fig.20. Schema instalatiei de generare a energiei electrice dotata cu turbina cu gaz 1 - motor electric; 2 - cuplaj; 3 - compresor de aer; 4 - aer comprimat; 5 - gaze combustibile; 6 - camera de ardere; 7 - gaze arse; 8 - cuplaj mecanic; 9 - generator electric trifazat; 10 - retea electrica; 11 - evacuare gaze calde;12 - CAF; 13 - cos evacuare gaze. |
Instalatia care functioneaza cu o turbina cu gaze este deosebit de complicata si ea este alcatuita din mai multe componente deoarece in turbina propriu-zisa are loc o singura faza deoarece celelalte procese se desfasoara in echipamente separate de turbina.Conectarea turbinei se face in doua variante posibile: a) clasic; b) in sistem de cogenerare. In sistemul clasic instalatia este alcatuita din motorul electric 1 care prin intermediul cuplajului mecanic 2 antreneaza turbocompresorul 3, figura 20.
|
2 p1 3 p0 1 4 v Fig. 21. Ciclul instalatiei de forta cu turbina cu gaze cu camera de ardere deschisa |
|
2 4 3 Fig. 22. Schema turbinei cu gaz 1 - arborele turbinei; 2 - admisia gazelor; 3 - rotor montat pe arbore; 4 - stator paletat pentru dirijarea gazelor spre urmatorul rotor; 5 - evacuarea gazelor din turbina |
Necesitatea turbocompresorului deriva din faptul ca arderea combustibilului gazos trebuie sa se faca cu exces de aer. Aerul comprimat este dirijatspre instalatia de ardere 6 in care vine in contact cu combustibilul injectat si pulverizat (cel lichid) cat mai fin pentru o ardere completa. In camera de ardere se poate introduce orice tip de combustibil de exemplu solid - praf de carbune, lichid - motorina, pacura, petrol, kerosen etc., gazos - gaz metan, gaz de fermentatie. Procesele de ardere se pot desfasura, teoretic, fie izobar, fie izocor. Instalatiile de ardere la regim izocor sunt mai putin folosite deoarece aduc complicatii constructive prin necesitatea mentinerii volumului constant - supapa cu inchidere si etanseitate corecta si rezistente la mare presiune. Gazele arse 7 au la intrarea in turbina 7008000C si ele trec prin turbina cu gaze antrenand rotorul in miscarea de rotatie. Rotorul, prin intermediul cuplajului mecanic 8 - figura 20, antreneaza generatorul electric 9 dupa care gazele arse sunt evacuate pe cosul 13 in atmosfera. Asadar,in varianta clasicadintr-o forma de energie primara se obtine o singura forma de energie - cea electrica prin intermediul energiei calorice. Este evident ca gazele arse au inca o incarcare termica care se poate recupera si folosi.
In varianta moderna se aplica principiul cogenerarii in care dintr-o forma de energie primara (combustibilul fosil) se obtin doua forme de energie: cea electrica prin intermediul generatorului electric si respectiv calorica la trecerea gazelor arse, dupa iesirea din turbina, printr-un cazan de apa calda - CAF. In acest mod se creeaza solutii rationale de utilizare a energiei primare cu un randament global de peste 95%.
|
Fig. 23. Schema amplasarii paletelor rotorice si statorice din turbina cu gaze 1 - admisia gazelor; 2 - ajutaje; 3 - rotor; 4 - stator paletat; 5 - evacuare gaze |
In instalatiile de forta cu camera de ardere deschisa - izobare - se realizeaza arderea in conditii de curent turbulent prin formarea unui front stabil al flacarii. Reprezentarea grafica a transformarilor de stare suferite de agentul motor in timpul scurgerii prin instalatie conduce la conturul 1234 din figura 21. In ciclu apar: 1-2 comprimarea adiabata, 2-3 arderea izocora, 3-4 destinderea adiabata a gazelor arse. Apare logic ca este necesara racirea gazelor de ardere dupa destindere pana la presiunea p0 in sensul transformarii izobare 4-1 - instalatia de cogenerare.
Rotorul turbinei cu gaze are mai multe etaje cu diametre diferite pe masura cedarii energiei si a reducerii presiunii, figura 22. Gazele trec prin ajutaje destinate sa transforme energia de presiune in energie cinetica; in acest mod creste viteza de curgere a gazelor prin masina. Cu aceasta viteza marita gazele trec printre paletele rotorului, profilate aerodinamic, cedand o parte din energie pe care o transforma in lucru mecanic de invartire a rotorului. Intre rotoare exista statoare cu palete profilate care dirijeaza gazele la urmatoarele palete rotorice, figura 23.
Se introduc doi coeficienti functionali:
a) raportul de crestere a presiunii in compresor b = p1/p0 = 67 - actual la constructiile moderne 11;
b) gradul de crestere al temperaturii in sistem a = T2/T0 - rapportul temperaturii gazelor la intrarea in turbina si la intrarea in compresor, cu a = 33,5 pentru o treapta.
Prin interpretarea liniilor de transformare din diagrama data in figura 21 se poate scrie:
a) comprimarea adiabata pe linia 12, ![]() din care rezulta valoarea
volumului din punctul 1 sub forma
din care rezulta valoarea
volumului din punctul 1 sub forma 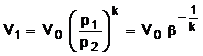
b) cresterea temperaturii se obtine prin
legea 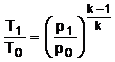 din care rezulta temperatura
din care rezulta temperatura ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5460
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved