| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Fie reactia de echilibru generala care decurge in faza omogena gazoasa:
aA + bB Û cC + dD
Guldberg si Waage (1867) au stabilit legea actiunii maselor conform careia la echilibru raportul dintre produsul concentratiilor produsilor de reactie si produsul concentratiilor reactantilor este constant. Matematic, legea se scrie astfel:
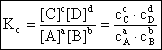 (6.1)
(6.1)
unde: Kc = constanta de echilibru a reactiei exprimata prin concentratii molare.
Pentru reactia chimica caracterizata prin gradul de avansare sau de conversie infinitezimal dξ avem:
![]() (6.2)
(6.2)
Din sirul de egalitati (6.2) rezulta:
dni = id (6.3)
unde: + i = coeficientii stoechiometrici ai produsilor de reactie;
- i = coeficientii stoechiometrici ai reactantilor.
La echilibru, in conditii izoterm-izobare, dG = 0.
Conform relatiei (4.191):
dG = -SdT + Vdp + ![]()
Rezulta ca:
![]() (6.4)
(6.4)
Cum insa d ≠ 0, avem:
![]() (6.5)
(6.5)
In acord cu egalitatea (6.5):
A = Gr = = c C + d D - (a A + b B (6.6)
Considerand ca reactia are loc intr-un sistem de gaze
perfecte si inlocuind valorile potentialelor chimice prin relatia (4.201) sub
forma ![]() , se
obtine din expresia (6.6) dupa rearanjarea termenilor:
, se
obtine din expresia (6.6) dupa rearanjarea termenilor:
![]() (6.7)
(6.7)
unde: pA, pB, pC, pD = presiunile partiale ale reactantilor si produsilor de reactie.
Relatia (6.7) poate fi scrisa sub forma:
![]() (6.8)
(6.8)
respectiv
![]() (6.9)
(6.9)
Deoarece = const., rezulta ca:
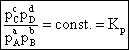 (6.10)
(6.10)
unde: Kp = constanta de echilibru a reactiei exprimata prin presiuni partiale.
Relatia (6.10) reprezinta o alta forma a legii actiunii maselor sau legea echilibrului chimic.
Ecuatia (6.8) poate fi scrisa sub forma:
![]() (6.11)
(6.11)
unde: ![]() = entalpia libera standard a reactiei;
= entalpia libera standard a reactiei;
R = constanta generala a gazelor.
Ecuatia (6.11) se numeste izoterma de reactie van't Hoff.
La echilibru, Gr = 0, adica ecuatia (6.11) devine:
![]() (6.12)
(6.12)
Constanta de echilibru poate fi exprimata si cu ajutorul fractiilor molare:
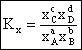 (6.13)
(6.13)
unde: Kx = constanta de echilibru exprimata prin fractii molare.
Daca reactia la echilibru are loc intre gaze reale atunci pentru a exprima constanta de echilibru se folosesc activitatile:
![]() (6.14)
(6.14)
unde: f = factor de activitate ce reprezinta corectia concentratiei molare;
a = activitate practica;
K = constanta termodinamica de echilibru.
respectiv:
![]() (6.15)
(6.15)
unde: a = activitate rationala;
= factor de activitate ce reprezinta corectia fractiei molare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3529
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved