| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Do the Laws of
Introduction
There is a view about laws of nature that is so deeply entrenched that it does not even have a name of its own. It is the view that laws of nature describe facts about reality. If we think that the facts described by a law obtain, or at least that the facts that obtain are sufficiently like those described in the law, we count the law true, or true-for-the-nonce, until further facts are discovered. I propose to call this doctrine the facticity view of laws. (The name is due to John Perry.)
It is customary to take the fundamental explanatory laws of physics as the ideal. Maxwell's equations, or Schroedinger's, or the equations of general relativity, are paradigms, paradigms upon which all other lawslaws of chemistry, biology, thermodynamics, or particle physicsare to be modelled. But this assumption confutes the facticity view of laws. For the fundamental laws of physics do not describe true facts about reality. Rendered as descriptions of facts, they are false; amended to be true, they lose their fundamental, explanatory force.
To understand this claim, it will help to contrast biology with physics. J. J. C. Smart argues that biology has no genuine laws of its own.1 It resembles engineering. Any general claim about a complex system, such as a radio or a living organism, will be likely to have exceptions. The generalizations of biology, or engineering's rules of thumb, are not true laws because they are not exceptionless. Many (though not Smart himself) take this to mean that biology is a second-rate science. If this is good reasoning, it must be physics that is the second-rate science. Not only do the laws of physics have exceptions; unlike biological laws, they are not even true for the most part, or approximately true.
end p.54
The view of laws with which I beginLaws of nature describe facts about realityis a pedestrian view that, I imagine, any scientific realist will hold. It supposes that laws of nature tell how objects of various kinds behave: how they behave some of the time, or all of the time, or even (if we want to prefix a necessity operator) how they must behave. What is critical is that they talk about objectsreal concrete things that exist here in our material world, things like quarks, or mice, or genes; and they tell us what these objects do.
Biological laws provide good examples. For instance, here is a generalization taken from a Stanford text on chordates:
The gymnotoids [American knife fish] are slender fish with enormously long anal fins, which suggest the blade of a knife of which the head is a handle. They often swim slowly with the body straight by undulating this fin. They [presumably always or for the most part] are found in Central and South America . . . Unlike the characins they [usually?] hide by day under river banks or among roots, or even bury themselves in sand, emerging only at night.2
The fundamental laws of physics, by contrast, do not tell what the objects in their domain do. If we try to think of them in this way, they are simply false, not only false but deemed false by the very theory that maintains them. But if physics' basic, explanatory laws do not describe how things behave, what do they do? Once we have given up facticity, I do not know what to say. Richard Feynman, in The Character of Physical Law, offers an idea, a metaphor. Feynman tells us There is . . . a rhythm and a pattern between the phenomena of nature which is not apparent to the eye, but only to the eye of analysis; and it is these rhythms and patterns which we call Physical Laws . . . 3 Most philosophers will want to know a lot more about how these rhythms and patterns function. But at least Feynman does not claim that the laws he studies describe the facts.
I say that the laws of physics do not provide true descriptions of reality. This sounds like an anti-realist doctrine. Indeed it is, but to describe the claim in this way may be misleading. For anti-realist views in the philosophy of science are traditionally of two kinds. Bas van Fraassen4 is a modern advocate of one of these versions of anti-realism; Hilary Putnam5 of the other. Van Fraassen is a sophisticated instrumentalist. He worries about the existence of unobservable entities, or rather, about the soundness of our grounds for believing in them; and he worries about the evidence which is supposed to support our theoretical claims about how these entities behave. But I have no quarrel with theoretical entities; and for the moment I am not concerned with how we know what they do. What is troubling me here is that our explanatory laws do not tell us what they do. It is in fact part of their explanatory role not to tell.
Hilary Putnam in his version of internal realism also maintains that the laws of physics do not represent facts about reality. But this is because nothingnot even the most commonplace claim about the cookies which are burning in the ovenrepresents facts about reality. If anything did, Putnam would probably think that the basic equations of modern physics did best. This is the claim that I reject. I think we can allow that all sorts of statements represent facts of nature, including the generalizations one learns in biology or engineering. It is just the fundamental explanatory laws that do not truly represent. Putnam is worried about meaning and reference and how we are trapped in the circle of words. I am worried about truth and explanation, and how one excludes the other.
Explanation by Composition of Causes, and the Trade-Off of Truth and Explanatory Power
Let me begin with a law of physics everyone knowsthe law of universal gravitation. This is the law that Feynman
end p.56
uses for illustration; he endorses the view that this law is the greatest generalization achieved by the human mind.6
In words, Feynman tells us:
The Law of Gravitation is that two bodies exert a force between each other which varies inversely as the square of the distance between them, and varies directly as the product of their masses.7
Does this law truly describe how bodies behave?
Assuredly not. Feynman himself gives one reason why. Electricity also exerts forces inversely as the square of the distance, this time between charges . . . 8 It is not true that for any two bodies the force between them is given by the law of gravitation. Some bodies are charged bodies, and the force between them is not Gmm′/r2. Rather it is some resultant of this force with the electric force to which Feynman refers.
For bodies which are both massive and charged, the law of universal gravitation and Coulomb's law (the law that gives the force between two charges) interact to determine the final force. But neither law by itself truly describes how the bodies behave. No charged objects will behave just as the law of universal gravitation says; and any massive objects will constitute a counterexample to Coulomb's law. These two laws are not true; worse, they are not even approximately true. In the interaction between the electrons and the protons of an atom, for example, the Coulomb effect swamps the gravitational one, and the force that actually occurs is very different from that described by the law of gravity.
There is an obvious rejoinder: I have not given a complete statement of these two laws, only a shorthand version. The Feynman version has an implicit ceteris paribus modifier in front, which I have suppressed. Speaking more carefully, the law of universal gravitational is something like this:
end p.57
If there are no forces other than gravitational forces at work, then two bodies exert a force between each other which varies inversely as the square of the distance between them, and varies directly as the product of their masses.
I will allow that this law is a true law, or at least one that is held true within a given theory. But it is not a very useful law. One of the chief jobs of the law of gravity is to help explain the forces that objects experience in various complex circumstances. This law can explain in only very simple, or ideal, circumstances. It can account for why the force is as it is when just gravity is at work; but it is of no help for cases in which both gravity and electricity matter. Once the ceteris paribus modifier has been attached, the law of gravity is irrelevant to the more complex and interesting situations.
This unhappy feature is characteristic of explanatory laws. I said that the fundamental laws of physics do not represent the facts, whereas biological laws and principles of engineering do. This statement is both too strong and too weak. Some laws of physics do represent facts, and some laws of biologyparticularly the explanatory lawsdo not. The failure of facticity does not have so much to do with the nature of physics, but rather with the nature of explanation. We think that nature is governed by a small number of simple, fundamental laws. The world is full of complex and varied phenomena, but these are not fundamental. They arise from the interplay of more simple processes obeying the basic laws of nature. (Later essays will argue that even simple isolated processes do not in general behave in the uniform manner dictated by fundamental laws.)
This picture of how nature operates to produce the subtle and complicated effects we see around us is reflected in the explanations that we give: we explain complex phenomena by reducing them to their more simple components. This is not the only kind of explanation we give, but it is an important and central kind. I shall use the language of John Stuart Mill, and call this explanation by composition of causes.9
It is characteristic of explanations by composition of
end p.58
causes that the laws they employ fail to satisfy the requirement of facticity. The force of these explanations comes from the presumption that the explanatory laws act in combination just as they would act separately. It is critical, then, that the laws cited have the same form, in or out of combination. But this is impossible if the laws are to describe the actual behaviour of objects. The actual behaviour is the resultant of simple laws in combination. The effect that occurs is not an effect dictated by any one of the laws separately. In order to be true in the composite case, the law must describe one effect (the effect that actually happens); but to be explanatory, it must describe another. There is a trade-off here between truth and explanatory power.
How Vector Addition Introduces Causal Powers
Our example, where gravity and electricity mix, is an example of the composition of forces. We know that forces add vectorially. Does vector addition not provide a simple and obvious answer to my worries? When gravity and electricity are both at work, two forces are produced, one in accord with Coulomb's law, the other according to the law of universal gravitation. Each law is accurate. Both the gravitational and the electric force are produced as described; the two forces then add together vectorially to yield the total resultant force.
The vector addition story is, I admit, a nice one. But it is just a metaphor. We add forces (or the numbers that represent forces) when we do calculations. Nature does not add forces. For the component forces are not there, in any but a metaphorical sense, to be added; and the laws that say they are there must also be given a metaphorical reading. Let me explain in more detail.
The vector addition story supposes that Feynman has left something out in his version of the law of gravitation. In the way that he writes it, it sounds as if the law describes the resultant force exerted between two bodies, rather than a component forcethe force which is produced between the two bodies in virtue of their gravitational
end p.59
masses (or, for short, the force due to gravity). A better way to state the law would be
Two bodies produce a force between each other (the force due to gravity) which varies inversely as the square of the distance between them, and varies directly as the product of their masses.
Similarly, for Coulomb's law
Two charged bodies produce a force between each other (the force due to electricity) which also varies inversely as the square of the distance between them, and varies directly as the product of their masses.
These laws, I claim, do not satisfy the facticity requirement. They appear, on the face of it, to describe what bodies do: in the one case, the two bodies produce a force of size Gmm′/r2; in the other, they produce a force of size qq′/r2. But this cannot literally be so. For the force of size Gmm′/r2 and the force of size qq′/r2. are not real, occurrent forces. In interaction a single force occursthe force we call the resultantand this force is neither the force due to gravity nor the electric force. On the vector addition story, the gravitational and the electric force are both produced, yet neither exists.
Mill would deny this. He thinks that in cases of the composition of causes, each separate effect does existit exists as part of the resultant effect, just as the left half of a table exists as part of the whole table. Mill's paradigm for composition of causes is mechanics. He says:
In this important class of cases of causation, one cause never, properly speaking, defeats or frustrates another; both have their full effect. If a body is propelled in two directions by two forces, one tending to drive it to the north, and the other to the east, it is caused to move in a given time exactly as far in both directions as the two forces would separately have carried it . . .10
Mill's claim is unlikely. Events may have temporal parts, but not parts of the kind Mill describes. When a body has moved along a path due north-east, it has travelled neither due north nor due east. The first half of the motion can be a part of the total motion; but no pure north motion can be a part of a motion that always heads northeast. (We learn this from Judith Jarvis Thomson's Acts and Other Events.) The lesson is even clearer if the example is changed a little: a body is pulled equally in opposite directions. It does not budge, but in Mill's picture it has been caused to move both several feet to the left and several feet to the right. I realize, however, that intuitions are strongly divided on these cases; so in the next section I will present an example for which there is no possibility of seeing the separate effects of the composed causes as part of the effect which actually occurs.
It is implausible to take the force due to gravity and the force due to electricity literally as parts of the actually occurring force. Is there no way to make sense of the story about vector addition? I think there is, but it involves giving up the facticity view of laws. We can preserve the truth of Coulomb's law and the law of gravitation by making them about something other than the facts: the laws can describe the causal powers that bodies have.
Hume taught that the distinction, which we often make betwixt power and the exercise of it, is . . . without foundation.11 It is just Hume's illicit distinction that we need here: the law of gravitation claims that two bodies have the power to produce a force of size Gmm′/r2. But they do not always succeed in the exercise of it. What they actually produce depends on what other powers are at work, and on what compromise is finally achieved among them. This may be the way we do sometimes imagine the composition of causes. But if so, the laws we use talk not about what bodies do, but about the powers they possess.
The introduction of causal powers will not be seen as a very productive starting point in our current era of moderate empiricism. Without doubt, we do sometimes think in terms of causal powers, so it would be foolish to maintain that the facticity view must be correct and the use of causal powers a total mistake. But facticity cannot be given up easily. We need an account of what laws are, an account that connects them, on the one hand, with standard scientific methods
end p.61
for confirming laws, and on the other, with the use they are put to for prediction, construction, and explanation. If laws of nature are presumed to describe the facts, then there are familiar, detailed philosophic stories to be told about why a sample of facts is relevant to their confirmation, and how they help provide knowledge and understanding of what happens in nature. Any alternative account of what laws of nature do and what they say must serve at least as well; and no story I know about causal powers makes a very good start.
The Force Due to Gravity
It is worth considering further the force due to gravity and the force due to electricity, since this solution is frequently urged by defenders of facticity. It is one of a class of suggestions that tries to keep the separate causal laws in something much like their original form, and simultaneously to defend their facticity by postulating some intermediate effect which they produce, such as a force due to gravity, a gravitational potential, or a field.
Lewis Creary has given the most detailed proposal of this sort that I know. Creary claims that there are two quite different kinds of laws that are employed in explanations where causes composelaws of causal influence and laws of causal action. Laws of causal influence, such as Coulomb's law and the law of gravity, tell us what forces or other causal influences operate in various circumstances, whereas laws of causal action tell us what the results are of such causal influences, acting either singly or in various combinations.12 In the case of composition of forces, the law of interaction is a vector addition law, and vector addition laws permit explanations of an especially satisfying sort because the analysis not only identifies the different component causal influences at work, but also quantifies their relative importance.13 Creary also describes less satisfying kinds of composition, including reinforcement, interference,
end p.62
and predomination. On Creary's account, Coulomb's law and the law of gravity come out true because they correctly describe what influences are producedhere, the force due to gravity and the force due to electricity. The vector addition law then combines the separate influences to predict what motions will occur.
This seems to me to be a plausible account of how a lot of causal explanation is structured. But as a defence of the truth of fundamental laws, it has two important drawbacks. First, in many cases there are no general laws of interaction. Dynamics, with its vector addition law, is quite special in this respect. This is not to say that there are no truths about how this specific kind of cause combines with that, but rather that theories can seldom specify a procedure that works from one case to another. Without that, the collection of fundamental laws loses the generality of application which Creary's proposal hoped to secure. The classical study of irreversible processes provides a good example of a highly successful theory that has this failing. Flow processes like diffusion, heat transfer, or electric current ought to be studied by the transport equations of statistical mechanics. But usually, the model for the distribution functions and the details of the transport equations are too complex: the method is unusable. A colleague of mine in engineering estimates that 90 per cent of all engineering systems cannot be treated by the currently available methods of statistical mechanics. We analyze them by whatever means seem appropriate for the problem at hand, he adds.14
In practice engineers handle irreversible processes with old
fashioned phenomenological laws describing the flow (or flux) of the quantity
under study. Most of these laws have been known for quite a long time. For
example there is Fick's law, dating from 1855, which relates the diffusion
velocity of a component in a mixture to the gradient of its density (J m
= − D∂c/∂x). Equally simple laws describe other
processes: Fourier's law for heat flow,
end p.63
in t (e.g. the J m in Fick's law cited above is dm/dt), giving the time rate of change of the desired quantity (in the case of Fick's law, the mass). Hence a solution at one time completely determines the quantity at any other time. Given that the quantity can be controlled at some point in a process, these equations should be perfect for determining the future evolution of the process. They are not.
The trouble is that each equation is a ceteris paribus law. It describes the flux only so long as just one kind of cause is operating. More realistic examples set different forces at play simultaneously. In a mixture of liquids, for example, if both the temperatures and the concentrations are non-uniform, there may be a flow of liquid due not only to the concentration gradients but also to the temperature gradients. This is called the Soret effect.
The situation is this. For the several fluxes J we have laws of the form,
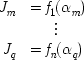
Each of these is appropriate only when its α is the only relevant variable. For cross-effects we require laws of the form.
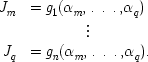
This case is structurally just like the simple causal examples that I discussed in the last essay. We would like to have laws that combine different processes. But we have such laws only in a few special cases, like the Soret effect. For the Soret effect we assume simple linear additivity in our law of action, and obtain a final cross-effect law by adding a thermal diffusion factor into Fick's law. But this law of causal action is highly specific to the situation and will not work for combining arbitrary influences studied by transport theory.
end p.64
Are there any principles to be followed in modifying to allow for cross-effects? There is only one systematic account of cross-effect modification for flow processes. It originated with Onsager in 1931, but was not developed until the 1950s. Onsager theory defines force-flux pairs, and prescribes a method for writing cross-effect equations involving different forces. As C. A. Truesdell describes it, Onsagerism claims to unify and correlate much existing knowledge of irreversible processes.15 Unfortunately it does not succeed. Truesdell continues:
As far as concerns heat conduction, viscosity, and diffusion . . . this is not so. Not only does Onsagerism not apply to any of these phenomena without a Procrustean force-fit, but even in the generous interpretation of its sectaries it does not yield as much reduction for the theory of viscosity as was known a century earlier and follows from fundamental principles. . . .16
Truesdell claims that the principles used in Onsager theory are vacuous. The principles must sometimes be applied in one way, sometimes in another, in an ad hoc fashion demanded by each new situation. The prescription for constructing laws, for example, depends on the proper choice of conjugate flux-force pairs. Onsager theory offers a general principle for making this choice, but if the principle were followed literally, we would not make the proper choice in even the most simple situations. In practice on any given occasion the choice is left to the physicist's imagination. It seems that after its first glimmer of generality the Onsager approach turns out to be a collection of ad hoc techniques.
I have illustrated with statistical mechanics; but this is not a special case. In fact classical mechanics may well be the only discipline where a general law of action is always available. This limits the usefulness of Creary's idea. Creary's scheme, if it works, buys facticity, but it is of little benefit to realists who believe that the phenomena of nature flow from a small number of abstract, fundamental laws. The fundamental laws will be severely limited in scope. Where the laws of action go case by case and do not fit a general scheme, basic laws of influence, like Coulomb's law and the law of gravity, may give true accounts of the influences that are produced; but the work of describing what the influences do, and what behaviour results, will be done by the variety of complex and ill-organized laws of action: Fick's law with correction factors, and the like. This fits better with my picture of a nature best described by a vast array of phenomenological laws tailored to specific situations, than with one governed in an orderly way from first principles.
The causal influences themselves are the second big draw-back to Creary's approach. Consider our original example. Creary changes it somewhat from the way I originally set it up. I had presumed that the aim was to explain the size and direction of a resultant force. Creary supposes that it is not a resultant force but a consequent motion which is to be explained. This allows him to deny the reality of the resultant force. We are both agreed that there cannot be three forces presenttwo components and a resultant. But I had assumed the resultant, whereas Creary urges the existence of the components.
The shift in the example is necessary for Creary. His scheme works by interposing an intermediate factorthe causal influencebetween the cause and what initially looked to be the effect. In the dynamic example the restructuring is plausible. Creary may well be right about resultant and component forces. But I do not think this will work as a general strategy, for it proliferates influences in every case. Take any arbitrary example of the composition of causes: two laws, where each accurately dictates what will happen when it operates in isolation, say C causes E and C′ causes E′'; but where C and C′ in combination produce some different effect, E″. If we do not want to assume that all three effectsE, E′, E″occur (as we would if we thought that E and E′ were parts of E″), then on Creary's proposal we must postulate some further occurrences, F and F′, as the proper effects of our two laws, effects that get combined by a law of action to yield E″ at the end. In some concrete cases the strategy will work, but in general I see no reason to think that these intermediate influences
end p.66
can always be found. I am not opposed to them because of any general objection to theoretical entities, but rather because I think every new theoretical entity which is admitted should be grounded in experimentation, which shows up its causal structure in detail. Creary's influences seem to me just to be shadow occurrences which stand in for the effects we would like to see but cannot in fact find.
A Real Example of the Composition of Causes
The ground state of the carbon atom has five distinct energy levels (see Figure 3.1). Physics texts commonly treat this phenomenon sequentially, in three stages. I shall follow the discussion of Albert Messiah in Volume II of Quantum Mechanics.17 In the first stage, the ground state energy is calculated by a central field approximation; and the single line (a) is derived. For some purposes, it is accurate to assume that only this level occurs. But some problems
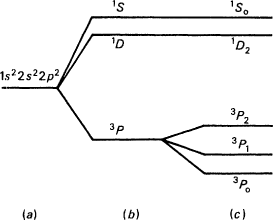
Fig. 3.1. The levels of the ground state of the carbon atom; (a) in the central field approximation (V 1 =V 2 =0); (b) neglecting spinorbit coupling (V 2 =0); (c) including spinorbit coupling. (Source: Messiah, Quantum Mechanics.)
end p.67
require a more accurate description. This can be provided by noticing that the central field approximation takes account only of the average value of the electrostatic repulsion of the inner shell electrons on the two outer electrons. This defect is remedied at the second stage by considering the effects of a term which is equal to the difference between the exact Coulomb interaction and the average potential used in stage one. This corrective potential splits the single line (a) into three lines depicted in (b).
But the treatment is inaccurate because it neglects spin effects. Each electron has a spin, or internal angular momentum, and the spin of the electron couples with its orbital angular momentum to create an additional potential. The additional potential arises because the spinning electron has an intrinsic magnetic moment, and an electron moving in [an electrostatic] potential sees a magnetic field.18 About the results of this potential Messiah tells us, Only the 3P state is affected by the spin-orbit energy term; it gets split into three levels: 3P 0 , 3P 1 and 3P 2 .19 Hence the five levels pictured in (c).
The philosophic perplexities stand out most at the last stage. The five levels are due to a combination of a Coulomb potential, and a potential created by spin-orbit coupling splits the lowest of these again into three. That is the explanation of the five levels. But how can we state the laws that it uses?
For the Coulomb effect we might try
Whenever a Coulomb potential is like that in the carbon atom, the three energy levels pictured in (b) occur.
(The real law will of course replace like that in the carbon atom by a mathematical description of the Coulomb potential in carbon; and similarly for the three energy levels pictured in (b).) The carbon atom itself provides a counter-example to this law. It has a Coulomb potential of the right kind; yet the five levels of (c) occur, not the three levels of (b).
end p.68
We might, in analogy with the vector addition treatment of composite forces, try instead
The energy levels produced by a Coulomb potential like that in the carbon atom are the three levels pictured in (b).
But (as with the forces produced by gravity in our earlier example) the levels that are supposed to be produced by the Coulomb potential are levels that do not occur. In actuality five levels occur, and they do not include the three levels of (b). In particular, as we can see from Messiah's diagram, the lowest of the three levelsthe 3Pis not identical with any of the five. In the case of the composition of motions, Mill tried to see the component effects as parts of the actual effect. But that certainly will not work here. The 3P level in (b) may be split and hence give rise to, the 3P 0 , 3P 1 , and 3P 2 levels in (c); but it is certainly not a part of any of these levels.
It is hard to state a true factual claim about the effects of the Coulomb potential in the carbon atom. But quantum theory does guarantee that a certain counterfactual is true; the Coulomb potential, if it were the only potential at work, would produce the three levels in (b). Clearly this counterfactual bears on our explanation. But we have no model of explanation that shows how. The covering-law model shows how statements of fact are relevant to explaining a phenomenon. But how is a truth about energy levels, which would occur in quite different circumstances, relevant to the levels which do occur in these? We think the counterfactual is important; but we have no account of how it works.
5. Composition of Causes Versus Explanation by Covering Law
The composition of causes is not the only method of explanation which can be employed. There are other methods, and some of these are compatible with the facticity view of laws. Standard covering-law explanations are a prime example.
Sometimes these other kinds of explanation are available
end p.69
even when we give an explanation which tells what the component causes of a phenomenon are. For example, in the case of Coulomb's law and the law of gravity, we know how to write down a more complex law (a law with a more complex antecedent) which says exactly what happens when a system has both mass and charge. Mill thinks that such super laws are always available for mechanical phenomena. In fact he thinks, This explains why mechanics is a deductive or demonstrative science, and chemistry is not.20
I want to make three remarks about these super laws and the covering explanations they provide. The first is familiar from the last essay: super laws are not always available. Secondly, even when they are available, they often do not explain much. Thirdly, and most importantly, even when other good explanations are to hand, if we fail to describe the component processes that go together to produce a phenomenon, we lose a central and important part of our understanding of what makes things happen.
|
(1) |
There are a good number of complex scientific phenomena which we are quite proud to be able to explain. As I urged in the last essay, for many of these explanations, super covering laws are not available to us. Sometimes we have every reason to believe that a super law exists. In other cases we have no good empirical reason to suppose even this much. Nevertheless, after we have seen what occurs in a specific case, we are often able to understand how various causes contributed to bring it about. We do explain, even without knowing the super laws. We need a philosophical account of explanations which covers this very common scientific practice, and which shows why these explanations are good ones. |
|
(2) |
Sometimes super laws, even when they are available to cover a case, may not be very explanatory. This is an old complaint against the covering-law model of explanation: Why does the quail in the garden bob its head up and down in that funny way whenever it walks? . . . Because they all do. In the example of spin-orbit coupling |
|
it does not explain the five energy levels that appear in a particular experiment to say All carbon atoms have five energy levels. |
|
|
(3) |
Often, of course, a covering law for the complex case will be explanatory. This is especially true when the antecedent of the law does not just piece together the particular circumstances that obtain on the occasion in question, but instead gives a more abstract description which fits with a general body of theory. In the case of spin-orbit coupling, Stephen Norman remarks that quantum mechanics provides general theorems about symmetry groups, and Hamiltonians, and degeneracies, from which we could expect to derive, covering-law style, the energy levels of carbon from the appropriate abstract characterization of its Hamiltonian, and the symmetries it exhibits. |
Indeed we can do this; and if we do not do it, we will fail to see that the pattern of levels in carbon is a particular case of a general phenomenon which reflects a deep fact about the effects of symmetries in nature. On the other hand, to do only this misses the detailed causal story of how the splitting of spectral lines by the removal of symmetry manages to get worked out in each particular case.
This two-faced character is a widespread feature of explanation. Even if there is a single set of super laws which unifies all the complex phenomena one studies in physics, our current picture may yet provide the ground for these laws: what the unified laws dictate should happen, happens because of the combined action of laws from separate domains, like the law of gravity and Coulomb's law. Without these laws, we would miss an essential portion of the explanatory story. Explanation by subsumption under super, unified covering laws would be no replacement for the composition of causes. It would be a complement. To understand how the consequences of the unified laws are brought about would require separate operation of the law of gravity, Coulomb's law, and so forth; and the failure of facticity for these contributory laws would still have to be faced.
end p.71
6. Conclusion
There is a simple, straightforward view of laws of nature which is suggested by scientific realism, the facticity view: laws of nature describe how physical systems behave. This is by far the commonest view, and a sensible one; but it does not work. It does not fit explanatory laws, like the fundamental laws of physics. Some other view is needed if we are to account for the use of laws in explanation; and I do not see any obvious candidate that is consistent with the realist's reasonable demand that laws describe reality and state facts that might well be true. There is, I have argued, a trade-off between factual content and explanatory power. We explain certain complex phenomena as the result of the interplay of simple, causal laws. But what do these laws say? To play the role in explanation we demand of them, these laws must have the same form when they act together as when they act singly. In the simplest case, the consequences that the laws prescribe must be exactly the same in interaction, as the consequences that would obtain if the law were operating alone. But then, what the law states cannot literally be true, for the consequences that would occur if it acted alone are not the consequences that actually occur when it acts in combination.
If we state the fundamental laws as laws about what happens when only a single cause is at work, then we can suppose the law to provide a true description. The problem arises when we try to take that law and use it to explain the very different things which happen when several causes are at work. This is the point of The Truth Doesn't Explain Much. There is no difficulty in writing down laws which we suppose to be true: If there are no charges, no nuclear forces, . . . then the force between two masses of size m and m′ separated by a distance r is Gmm′/r2. We count this law truewhat it says will happen, does happenor at least happens to within a good approximation. But this law does not explain much. It is irrelevant to cases where there are electric or nuclear forces at work. The laws of physics, I concluded, to the extent that they are true, do
end p.72
not explain much. We could know all the true laws of nature, and still not know how to explain composite cases. Explanation must rely on something other than law.
But this view is absurd. There are not two vehicles for explanation: laws for the rare occasions when causes occur separately; and another secret, nameless device for when they occur in combination. Explanations work in the same way whether one cause is at work, or many. Truth Doesn't Explain raises perplexities about explanation by composition of causes; and it concludes that explanation is a very peculiar scientific activity, which commonly does not make use of laws of nature. But scientific explanations do use laws. It is the laws themselves that are peculiar. The lesson to be learned is that the laws that explain by composition of causes fail to satisfy the facticity requirement. If the laws of physics are to explain how phenomena are brought about, they cannot state the facts.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1995
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved