| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
How the Measurement Problem Is an Artefact of the Mathematics
0. Introduction
Von Neumann's classic work of 1932 set the measurement problem in quantum mechanics.1 There are two kinds of evolution in the quantum theory, von Neumann said. The first kind is governed by Schroedinger's equation. It is continuous and deterministic. The second, called reduction of the wave packet, is discontinuous and indeterministic. It is described by von Neumann's projection postulate.
The terminology arises this way: classical systems have well-defined values for both position and momentum. Quantum systems, on the other hand, may have no well-defined value for either. In this case they are said to be in a superposition of momentum states, or of position states. Consider position. An electron will frequently behave not like a particle, but like a wave. It will seem to be spread out in space. But when a measurement is made we always find it at a single location. The measurement, we say, reduces the wave packet; the electron is projected from a wave-like state to a particle-like state.
But what is special about measurement? Most of the time systems are governed by the Schroedinger equation. Reductions occur when and only when a measurement is made. How then do measurements differ from other interactions between systems? It turns out to be very difficult to find any difference that singles out measurements uniquely. Von Neumann postulated that measurements are special because they involve a conscious observer. Eugene Wigner concurred and I think this is the only solution that succeeds in picking measurements from among all other interactions.
It is clearly not a very satisfactory solution. The measurement problem is one of the long-standing philosophical difficulties that troubles the quantum theory.
I will argue here that the measurement problem is not a real problem. There is nothing special about measurement. Reductions of the wave packet occur in a wide variety of other circumstances as well, indeterministically and on their own, without the need for any conscious intervention. Section 1 argues that reductions occur whenever a system is prepared to be in a given microscopic state. Section 2 urges that reductions occur in other transition processes as well, notably in scattering and in decay. There is good reason for attending to these transition processes. On the conventional interpretation, which takes position probabilities as primary, quantum propositions have a peculiar logic or a peculiar probability structure or both. But transition processes, where reductions of the wave packet occur, have both a standard logic and a standard probability. They provide a non-problematic interpretation for the theory.
The proposal to develop an interpretation for quantum mechanics based on transition probabilities seems to me exactly right. But it stumbles against a new variation of the measurement problem. Two kinds of evolution are postulated. Reductions of the wave packet are no longer confined to measurements, but when do they occur? If there are two different kinds of change, there must be some feature which dictates which situations will be governed by Schroedinger's law and which by the projection postulate. The very discipline that best treats transitions suggests an answer. Quantum statistical mechanics provides detailed treatments of a variety of situations where reduction seems most plausibly to occur. This theory offers not two equations, but one. In general formulations of quantum statistical mechanics, Schroedinger's evolution and reduction of the wave packet appear as special cases of a single law of motion which governs all systems equally. Developments of this theory offer hope, I urge in Section 4, for eliminating the measurement problem and its variations entirely. The two evolutions are not different in nature; their difference is an artefact of the conventional notation.
1. In Defence of Reduction of the Wave Packet
In 1975 I wrote Superposition and Macroscopic Observation. Here is the problem that I set in that paper:
Macroscopic states, it appears, do not superpose. Macroscopic bodies seem to possess sharp values for all observable quantities simultaneously.
But in at least one well-known situationthat of measurementquantum mechanics predicts a superposition. It is customary to try to reconcile macroscopic reality and quantum mechanics by reducing the superposition to a mixture. This is a program that von Neumann commenced in 1932 and to which Wigner, Groenewold, and others have contributed. Von Neumann carried out his reduction by treating measurement as a special and unique case that is not subject to the standard laws of quantum theory. Subsequent work has confirmed that a normal Schroedinger evolution cannot produce the required mixture. This is not, however, so unhappy a conclusion as is usually made out. Quantum mechanics requires a superposition: the philosophical problem is not to replace it by a mixture, but rather to explain why we mistakenly believe that a mixture is called for.3
These are the words of a committed realist: the theory says that a superposition occurs; so, if we are to count the theory a good one, we had best assume it does so.
Today I hold no such view. A theory is lucky if it gets some of the results right some of the time. To insist that a really good theory would do better is to assume a simplicity and uniformity of nature that is belied by our best attempts to deal with it. In quantum mechanics in particular I think there is no hope of bringing the phenomena all under the single rule of the one Schroedinger equation. Reduction of the wave packet occurs as well, and in no systematic or uniform way. The idea that all quantum evolutions can be cast into the same abstract form is a delusion. To understand why, it is important to see how the realist programme that I defended in 1975 fails.
Quantum systems, we know, are not supposed to have
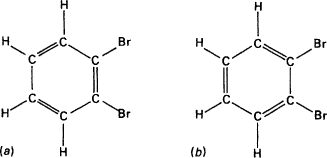
Fig 9.1. Orthodibromobenzene (Source: Feynman, Lectures on Physics.)
well-defined values for all of their variables simultaneously. A system with a precise momentum will have no position. It will behave like a wave, and be distributed across space. This is critical for the explanations that quantum mechanics gives for a variety of phenomena. The famous case of the bonding energy in benzene is a good example. This energy is much lower than would be expected if there were double bonds where they should be between the carbon atoms. The case is easier to see if we look at orthodibromobenzenethat is, benzene with two bromines substituted for two hydrogens. There are two possible structures (see Figure 9.1).
In fact all the forms in nature are the same. Do they have a single bond separating the bromines, as in 9.1a, or a double bond, as in 9.1b? Neither. The energy is in between that predicted from one bond and that predicted from two. It is as if there is a bond and a half. Linus Pauling said that each molecule resonates between the first arrangement and the second, and that is not far off the quantum answer. According to quantum mechanics the molecule is in a superposition of the two configurations. That means that it is neither in configuration 9.1a entirely, nor in 9.1b entirely, but in both simultaneously. Where then are the electrons that form the bonds? On a classical particle picture they must be located at one point or another. Quantum mechanics says that, like waves, they are smeared across the alternative locations.
This behaviour is not too disturbing in electrons. After all, they are very small and we do not have very refined intuitions about them. But it is not a correct account for macroscopic objects, whose positions, velocities, and such are narrowly fixed. How can we prevent smearing in macroscopic objects? First, we notice that smearing across one variable, like position, occurs only when an incompatible quantity, like momentum, is precisely defined. This suggests that all macroscopic observables are compatible. We can arrange this in the following way: admittedly, the real quantities that describe macroscopic systems will not all be compatible. But we do not actually observe the real value of a quantity at a time. Instead what we see is a long-time average over these valueslong compared to relaxation times in the objects themselves. By a coarse-grained averaging, we can construct new quantities that are all compatible. We then claim that these new quantities, and not the originals, are the macroscopic observables that concern us.
But this is not enough. The construction ensures that it is possible for macroscopic objects to be in states with well-defined values for all macroscopic observables. It is even possible that they would always evolve from one such state into another if left to themselves. But interactions with microscopic objects bring them into superpositions. That is what happens in a measurement according to the Schroedinger equation. The electron starts out in a superposition, with the apparatus in its ground state. Together the composite of the two finishes after the measurement in a superposition, where the pointer of the apparatus has no well-defined position but is distributed across the dial.
This is why von Neumann postulated that measurement is special. In the end measurement interactions are not governed by the Schroedinger equation. After the measurement has ceased, a new kind of change occurs. The superposed state of the apparatus-plus-object reduces to one of the components of the superposition. This kind of change is called reduction of the wave packet, and the principle that governs it is the projection postulate. The process is indeterministic: nothing decides which of the final states will occur, although the probabilities for each state are antecedently determined. In an ensemble of similar measurement interactions, there will be a mix of final states. So we sometimes say that a reduction of the wave packet takes superpositions into mixtures. But it is important to remember that this is a description entirely at the level of the ensemble. Individually, reduction of the wave packet takes superpositions into components of the superposition.
There are two obvious tests to see if von Neumann is right, and both tell in favour of reduction of the wave packet. The first looks at individuals. If the pointer is indeed in a superposition after a measurement, it should somehow be distributed across space. But in fact we always observe the pointer at a definite place. The second looks at ensembles. Mixtures and superpositions generate different statistical predictions about the future behaviour of the ensemble. Collections of macroscopic systems always behave, statistically, as if they were in mixtures. In Superposition and Macroscopic Observation I defend the superposition against both of these difficulties.
The first defence consists in breaking the eigenvalueeigenvector link. The discussion so far has assumed that the electron has no position value because it is in a superposition of position states. We have thus been adopting the principle: S has a value for a given observable (an eigenvalue) if and only if S is in the corresponding state (the eigenstate). To deny the inference in the direction from state to value would require serious revision of our understanding of quantum theory, which teaches that the probability in a given eigenstate for a system to exhibit the corresponding eigenvalue is one. But there is no harm in breaking the inference in the other direction. One must be careful not to run foul of various no-hidden-variable proofs, like those of Kochen and Specker4 and of J. S. Bell.5 But there are a variety of satisfactory ways of assigning values to systems in superpositions.6
Let us turn to the second difficulty. Why are physicists not much concerned with the measurement problem in practice? Here is a common answer: macroscopic objects have a very large number of degrees of freedom with randomly distributed phases. The effect of averaging over all of these degrees of freedom is to eliminate the interference terms that are characteristic of superpositions. In a very large system with uncorrelated phases the superposition will look exactly like a mixture. This argument is just like the one described in Essay 6 for deriving the exponential decay law. The atom is in interaction with the electromagnetic field. If it interacted with only one mode, or a handful of modes, it would oscillate back and forth as if it were in a superposition of excited and de-excited states. (There is a very nice discussion of this in P. C. W. Davies, The Physics of Time Asymmetry.)7 In fact it is in interaction with a quasi-continuum of modes, and averaging over them, as we do in the WeisskopfWigner approximation, eliminates the terms that represent the interference. An ensemble of such atoms evolving over time will look exactly as if it is in a mixture of excited and de-excited states, and not in a superposition.
There have been various attempts to apply these ideas more rigorously to measurement situations. The most detailed attempt that I know is in the work of Danieri, Loinger, and Prosperi.8 This is what I describe in Superposition and Macroscopic Observation. Daneri, Loinger, and Prosperi propose an abstract model of a measurement situation, and consider what happens in this model as the macroscopic apparatus comes to equilibrium after the interaction. They conclude that the superposition that the Schroedinger equation predicts will be statistically indistinguishable from the mixture predicted by the projection postulate. This is not to say that the superposition and the mixture are the same. There is no way under the Schroedinger equation for the system to end up in a genuine mixture. The claim of Daneri, Loinger, and Prosperi is weaker. Superpositions and mixtures make different statistical predictions. But in this case, the two will agree on predictions about all macroscopic observables. The superposition and the mixture are different, but the difference is not one we can test directly with our macroscopic instruments.
Formally, there is an exact analogue between measurement in the treatment of Daneri, Loinger, and Prosperi and the case of exponential decay. In deriving the exponential decay law, we do not produce, in approximation, a mixture as the final state. Rather we show that the superposition is indistinguishable from a mixture with respect to a certain limited set of test variables.
Jeffrey Bub9 and Hilary Putnam10 have both attacked the Daneri, Loinger, and Prosperi programme. They do not object to the details of the measurement model. Their objection is more fundamental. Even if the model is satisfactory, it does not solve the problem. A superposition is still a superposition, even if it dresses up as a mixture. We want to see a mixture at the conclusion of the measurement. It is no credit to the theory that the superposition which it predicts looks very much like a mixture in a variety of tests. I now argue that a correct account will produce a mixture for the final state. But in 1975 I thought that Bub and Putnam had the situation backwards. Theirs is exactly the wrong way for a realist to look at the work of Daneri, Loinger, and Prosperi. The theory predicts a superposition, and we should assume that the superposition occurs. The indistinguishability proof serves to account for why we are not led into much difficulty by the mistaken assumption that a mixture is produced.
That was the argument I gave in 1975 in defence of the Schroedinger equation. Now I think that we cannot avoid admitting the projection postulate, and for a very simple reason: we need reduction of the wave packet to account for the behaviour of individual systems over time. Macroscopic systems have orderly histories. A pointer that at one instant rests in a given place is not miraculously somewhere else the next. That is just what reduction of the wave packet guarantees. After the measurement the pointer is projected onto an eigenstate of position. Its behaviour will thereafter be governed by that stateand that means it will behave over time exactly as we expect.
There is no way to get this simple result from a superposition. Following the lines of the first defence above, we can assign a location to the pointer even though it is in a superposition. An instant later, we can again assign it a position. But nothing guarantees that the second position will be the time-evolved of the first. The Daneri, Loinger, and Prosperi proof, if it works, shows that the statistical distributions in a collection of pointers will be exactly those predicted by the mixture at any time we choose to look. But it does not prove that the individuals in the collection will evolve correctly across time. Individuals can change their values over time as erratically as they please, so long as the statistics on the whole collection are preserved.
This picture of objects jumping about is obviously a crazy picture. Of course individual systems do not behave like that. But the assumption that they do not is just the assumption that the wave packet is reduced. After measurement each and every individual system behaves as if it really is in one or another of the components and not as if it is in a superposition. There are in the literature a few treatments for some specific situations that attempt to replicate this behaviour theoretically but there is no good argument that this can be achieved in general. One strategy would be to patch up the realist account by adding constraints: individual values are to be assigned in just the right way to guarantee that they evolve appropriately in time. But if the superposition is never again to play a role, and in fact the systems are henceforth to behave just as if they were in the component eigenstates, to do this is just to admit reduction of the wave packet without saying so. On the other hand what role can the superposition play? None, if macroscopic objects have both well-defined values and continuous histories.
So far we have been concentrating on macroscopic objects and how to keep them out of superpositions. In fact we need to worry about microscopic objects as well. Quantum systems, we have seen, are often in superpositions. The electron is located neither on one atom nor on another in the benzene molecule. In the next section we will see another example. When an electron passes a diffraction grating, it passes through neither one or another of the openings in the grating. More like a wave, it seems to go through all at once. How then do we get microsystems out of superpositions and into pure states when we need them? To study the internal structure of protons we bombard them at high velocity with electrons. For this we need a beam, narrowly focused, of very energetic electrons; that is, we need electrons with a large and well-defined momentum. The Stanford Linear Accelerator (SLAC) is supposed to supply this need. But how does it do so?
Here is a simple model of a linear accelerator (a drift tube linac)see Figure 9.2. The drift tube linac consists of two major parts: an injector and a series of drift tubes hooked up to an alternating voltage. The injector is a source of well-collimated electronsthat is, electrons which have a narrow spread in the direction of their momentum. We might get them this way: first, boil a large number of electrons off a hot wire. Then accelerate them with an electrostatic fieldfor example in a capacitor. Bend them with a magnet and screen all but a small range of angles. The resulting beam can be focused using a solenoid or quadrature magnets before entering the drift tube configuration for the major part of the particle's acceleration.

Fig 9.2. Model of a linear accelerator
172
Inside the drift tubes the electric field is always zero. In
the gaps it alternates with the generator frequency. Consider now a particle of
charge e that crosses the first gap at a time when the accelerating
field is at its maximum. The length L of the next tube is chosen so that
the particle arrives at the next gap when the field has changed sign. So again
the particle experiences the maximum accelerating voltage, having already
gained an energy 2eV To do this,
L must be equal to ![]() where
v is particle velocity and T the period of oscillation. Thus L
increases up to the limiting value: for
where
v is particle velocity and T the period of oscillation. Thus L
increases up to the limiting value: for ![]() .
.
The electron in the linac is like a ball rolling down a series of tubes. When it reaches the end of each tube, it drops into the tube below, gaining energy. While the ball is rolling down the second tube, the whole tube is raised to the height of the first. At the end the ball drops again. While it traverses the tube the ball maintains its energy. At every drop it gains more. After a two-mile acceleration at SLAC, the electrons will be travelling almost at the speed of light.
Imagine now that we want to bring this whole process under the Schroedinger equation. That will be very complicated, even if we use a simple diagrammatic model. Quantum systems are represented by vectors in a Hilbert space. Each system in the process is represented in its own Hilbert spacethe emitting atoms, the electrostatic field, the magnetic field, the absorbing screen, and the fields in each of the separate drift tubes. When two systems interact, their joint state is represented in the product of the Hilbert spaces for the components. As we saw in the discussion of measurement, the interaction brings the composite system into a superposition in the product space for the two. When a third system is added, the state will be a superposition in the product of three spaces. Adding a fourth gives us a superposition in a four-product space, and so on. At the end of the accelerator we have one grand superposition for the electrons plus capacitor plus magnet plus field-in-the-first-tube plus field-in-the-second, and so forth.
The two accounts of what happens are incompatible. We want an electron travelling in a specified direction with a well-defined energy. But the Schroedinger equation predicts a superposition for an enormous composite, in which the electron has neither a specific direction nor a specific energy. Navely, we might assume that the problem is solved early in the process. A variety of directions are represented when the electrons come off the wire or out of the capacitor, but the unwanted angles are screened out at the absorbing plate. If the formal Schroedinger treatment is followed, this solution will not do. The absorbing screen is supposed to produce a state with the momentum spread across only a very small solid angle. On the Schroedinger formalism there is no way for the absorbing screen to do this job. Interaction with the screen produces another superposition in a yet bigger space. If we are to get our beam at the end of the accelerator, Schroedinger evolution must give out. Reduction of the wave packet must occur somewhere in the preparation process.
This kind of situation occurs all the time. In our laboratories we prepare thousands of different states by hundreds of different methods every day. In each case a wave packet is reduced. Measurements, then, are not the only place to look for a failure of the Schroedinger equation. Any successful preparation will do.
2. Why Transition Probabilities Are Fundamental
Position probabilities play a privileged role in the interpretation of quantum mechanics. Consider a typical text. In the section titled The Interpretation of Ψ and the Conservation of Probability Eugen Merzbacher tells us, about the wave-function, Ψ:
Before going into mathematical details it would, however, seem wise to attempt to say precisely what Ψ is. We are in the paradoxical situation of having obtained an equation [the Schroedinger equation] which we believe is satisfied by this quantity, but of having so far given only a deliberately vague interpretation of its physical significance. We have regarded the wave function as a measure of the probability of finding the particle at time t at the position r. How can this statement be made precise?
Ψ itself obviously cannot be a probability. All hopes we might have entertained in that direction vanished when Ψ became a complex function, since probabilities are real and positive. In the face of this dilemma the next best guess is that the probability is proportional to |Ψ|2, the square of the amplitude of the wave function . . .
Of course, we were careless when we used the phrase probability of finding the particle at position r. Actually, all we can speak of is the probability that the particle is in a volume element d3r which contains the point r. Hence, we now try the interpretation that |Ψ(r, t 2d3r is proportional to the probability that upon a measurement of its position the particle will be found in the given volume element. The probability of finding the particle in some finite region of space is proportional to the integral of Ψ*Ψ over this region.11
So |Ψ(r 2 is a probability. That is widely acknowledged. But exactly what is |Ψ(r 2d3r the probability of? What is the event space that these quantum mechanical probabilities range over? There is no trouble-free answer. Merzbacher makes the conventional proposal, that |Ψ(r, t 2d3r is proportional to the probability that upon a measurement of its position the particle will be found in the given volume element. But why must we refer to measurement? We should first rehearse the difficulties that beset the far simpler proposal that |Ψ(r 2d3r represents the probability that the particle is located in the region around r, measured or not. This answer supposes that the events which quantum probabilities describe are the real locations of quantum objects. It has a hard time dealing with situations where interference phenomena are significantfor instance, the bonding of atoms in benzene molecule, or the wavelike patterns which are observed in a diffraction experiment.
The two-slit experiment is the canonical example. A beam of electrons passes through a screen with two holes and falls onto a photographic plate. Imagine that, at the time of passing the screen, each electron is located either at slit 1 (r = s or at slit 2 (r = s 2 ). Then we may reason as follows. An electron lands at a point y on the screen if and only if it lands at y and either passes through slit one or slit two, i.e.
So
It follows that
and, since s 1 and s 2 are disjoint
Now do the quantum mechanical calculation. If the source is
equidistant from both slit 1 and slit 2, the probability of passing through
slit 1 = probability of passing through slit ![]() ,
and the state of the electrons at the screen will be Ψ(y) =
1/√2φ 1 (y) + 1/√2φ 2 (y),
where φ 1 (y) is the state of an electron beam which has
passed entirely through slit 1; φ 2 (y), a beam
passing entirely through slit 2. So, using the quantum mechanical rule
,
and the state of the electrons at the screen will be Ψ(y) =
1/√2φ 1 (y) + 1/√2φ 2 (y),
where φ 1 (y) is the state of an electron beam which has
passed entirely through slit 1; φ 2 (y), a beam
passing entirely through slit 2. So, using the quantum mechanical rule
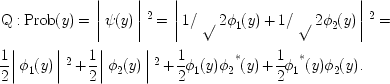
But identifying
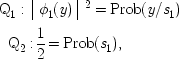
and similarly for s 2
, we see that the classical calculation C for the probability of landing at y,
and the quantum mechanical calculation Q do not give the same results. They
differ by the interference terms ![]() .
The C calculation is the one that supposes that the electrons have a definite
location at the screen and its consequences are not borne out in experiment.
.
The C calculation is the one that supposes that the electrons have a definite
location at the screen and its consequences are not borne out in experiment.
There are various ways to avoid the conclusion C well-rehearsed by now. The first insists that quantum mechanical propositions have a funny logic. In particular they do not obey the distributive law. This blocks the argument at the move between C 1 and C This solution was for a while persuasively urged by Hiliary Putnam.12 Putnam has now given it up because of various reflections on the meaning and use of the connective or; but I am most impressed by the objections of Michael Gardner13 and Peter Gibbins14 that the usual quantum logics do not in fact give the right results for the two-slit experiment.
The second well-known place to block the C derivation is between the third and the fourth steps. The first attempt maintained that quantum propositions have a peculiar logic; this attempt insists that they have a peculiar probability structure. It is a well-known fact about quantum mechanics that the theory does not define joint probabilities for non-commuting (i.e. incompatible) quantities. Position and momentum are the conventional examples. But the different positions of a single system at two different times are also incompatible quantities, and so their joint probabilities are also not defined. (The incompatibility of r at t and r at t′ is often proved on the way to deriving the theorem of Ehrenfest that, in the mean, quantum mechanical processes obey the classical equations of motion.) So Prob(y & s and Prob(y & s 2 ) from C 4 do not exist. If Prob(y) is to be calculated it must be calculated in some different waynotably, as in the Q derivation.
What does it mean in a derivation like this to deny a joint probability? After all, by the time of C 3 we have gone so far as to admit that each electron, individually, has a well-defined position at both the screen and at the plate. What goes wrong when we try to assign a probability to this conjunctive event? Operationally, the failure of joint distributions must show up like this. We may imagine charting finite histograms for the joint values of r at t and r at t′, but the histograms forever bounce about and never converge to a single curve. There is by hypothesis some joint frequency in every finite collection, but these frequencies do not approach any limit as the collections grow large. This may not seem surprising in a completely chaotic universe, but it is very surprising here where the marginal probabilities are perfectly well defined: in the very same collections, look at the frequencies for r at t or r′ at t separately. These frequencies can always be obtained by summing over the joint frequencies: e.g., in any collection the frequency (y) = frequency(y & s + frequency(y & s 2 ). As the collections grow larger, the sum approaches a limit, but neither of the terms in the sum do. This is peculiar probabilistic behaviour for a physical system. (Though since, as I remarked in the last essay, I am suspicious even of the corresponding probabilities in classical statistical mechanics, my own view is that it is considerably less peculiar than quantum logic.)
Before proceeding, it is important to notice that both attempts to begin with C 1 and to block the inference to C 4 depend on incompatibility. It is the incompatibility of location-when-passing-the-screen and location-at-the-plate that stops the inference from C 1 to C In conventional quantum logics, the distributive law holds if all the propositions are compatible. Similarly, the theory will always give a joint distribution for any two quantities that commute.
We began with the question, what are quantum probabilities probabilities of? Practitioners of quantum theory have been reluctant to adopt either non-standard logics or non-standard probabilities. They have rejected the first proposal altogether. Quantum probabilities are not probabilities that the system is located at r, but rather, as Merzbacher says, that it will be found at r in a position measurement. This answer is no more trouble-free than the first. It supposes that the electron passes through neither one slit nor the other when we are not looking. When we do look, there, suddenly, it is, either at the top slit or at the bottom. What is special about looking that causes objects to be places where they would not have been otherwise? This is just another version of the notorious measurement problem, which we first discussed in the last section.
I find neither of these two conventional answers very satisfactory, and I propose a more radical alternative. I want to eliminate position probabilities altogether, and along with them the probabilities for all the classic dynamic quantities. The only real probabilities in quantum mechanics, I maintain, are transition probabilities. In some circumstances a quantum system will make a transition from one state to another. Indeterministically and irreversibly, without the intervention of any external observer, a system can change its state: the quantum number of the new state will be different and a quantum of some conserved quantityenergy, or momentum, or angular momentum, or possibly even strangenesswill be emitted or absorbed. When such a situation occurs, the probabilities for these transitions can be computed; it is these probabilities that serve to interpret quantum mechanics.
I shall illustrate with a couple of examples: the first, exponential decay; and the second, the scattering of a moving particle by a stationary target. Whether in an atom when an outer shell electron changes orbit and a photon in given off, or in a nucleus resulting in α, β, or γ radiation, decay is the classic indeterministic process. Consider a collection of non-interacting atoms, each in an excited state. The number of atoms that continue to be in the excited state decreases exponentially in time. One by one the atoms decay, and when an atom decays, something concrete happensa photon is given off in a specific direction, the energy of the electromagnetic field is increased, and its polarization is affected. Which atom will decay, or when, is completely indeterministic. But the probability to decay is fixed, and this transition probability is the probability on which I want to focus.
The second example is from scattering theorya theory of critical importance in high energy physics, where fundamental particles are studied almost entirely through their behaviour in collisions. Consider a beam which traverses a very long tube of very small diameter and then collides with a target of massive particles and is scattered. If we ring the target with detectors, we will find that many of the incoming particles miss the target and continue in the forward direction. But a number of others will be scattered through a variety of angles. If the scattering is elastic, the incoming particles will change only their direction; in inelastic scattering the moving particles will exchange both momentum direction and energy with the target. The transition probabilities in this case are the probabilities for a particle whose momentum was initially in the forward direction to be travelling after scattering in another specific direction, and with a well-defined energy.
The transition probabilities that occur in scattering have a venerable history: they are the first to have been introduced into quantum mechanics. Max Born's preliminary paper of 1926 is generally agreed to provide the original proposal for interpreting the wave function probabilistically. The abstract of that paper reads: By means of an investigation of collision processes the viewpoint is developed that quantum mechanics in Schrdinger's form can be used to describe not only stationary states but also quantum jumps.15 Born treats a collision between a moving electron and an atom. In the middle of the paper he says
If one now wishes to understand this result in corpuscular
terms, then only one interpretation is possible: ![]() defines
the probability1 that the electron coming from the z-direction
will be projected in the direction defined by (α, β, γ) (and
with phase change δ), where its energy I has increased by a quantum
defines
the probability1 that the electron coming from the z-direction
will be projected in the direction defined by (α, β, γ) (and
with phase change δ), where its energy I has increased by a quantum
![]() at
the expense of the atomic energy.16
at
the expense of the atomic energy.16
The footnote is famous:
1. Remark added in proof corrections: More precise analysis
shows that the probability is proportional to the square of ![]() .17
.17
So probability entered quantum mechanics not as a position probability or a momentum probability, but rather as the transition probability that the electron coming from the z-direction will be projected in the direction defined by (α, β, γ).
I am urging that we give up position probabilities, momentum probabilities, and the like, and concentrate instead on transition probabilities. The advantage of transition probabilities is that they have a classical structure, and the event space over which they range has an ordinary Boolean logic. To understand why, we need for a moment to look at the formal treatment of transitions. Transitions occur in situations where the total Hamiltonian H is naturally decomposed into two partsH the free Hamiltonian in the situation, and V, a disturbing potential: H = H 0 + V. The system is assumed to begin in an eigenstate of H Supposing, as is the case in examples of transitions, that H 0 does not commute with V and hence does not commute with H, the eigenvalue of H 0 will not be conserved. Formally, the initial eigenstate of H 0 will evolve into a new state which will be a superposition of H 0 eigenstates: t) = Σc i (t)φ i where H 0 = Σα i |φ i ⟩⟨φ i |. The transition probabilities are given by the |c i (t 2. In the old language, they are the probabilities for a system initially in a given φ 0 to be or be found later, at t, in some one or another of the eigenstates φ i . The probabilities and the event space they range over are classical just because we look at no incompatible observables. It is as if we were dealing with the possessed values for H All observables we can generate from H 0 will be mutually compatible, and the logic of compatible propositions is classical. So too is the probability.
The primary consideration that has made philosophers favour quantum logic is the drive towards realism (though Alan Stairs18 lays out other, more enduring grounds). They want to find some way to ensure that a quantum system will possess values for all the classic dynamic quantitiesposition, momentum, energy, and the like. But this motivation is ill founded. If we want to know what properties are real in a theory, we need to look at what properties play a causal role in the stories the theory tells about the world. This is a point I have been urging throughout this book, and it makes a crucial difference here. Judged by this criterion, the classical dynamic quantities fare badly. The static values of dynamic variables have no effects; it is only when systems exchange energy or momentum, or some other conserved quantity, that anything happens in quantum mechanics. For example, knowing the position of a bound electron tells us nothing about is future behaviour, and its being located wherever it is brings about nothing. But if the electron jumps orbitsthat is, if the atom makes an energy transitionthis event has effects that show up in spectroscopic lines, in the dissolution of chemical bonds, in the formation of ions, and so on. This is true even for measurements of position. The detector does not respond to the mere presence of the system but is activated only when an exchange of energy occurs between the two. We need to consider an example that shows how transitions play a causal role in quantum mechanics which the conventional dynamic quantities do not. This seems a good one to use.
Henry Margenau19 has long urged that all quantum measurements are ultimately measures of position. But position measurements themselves are basically records of scattering interactions. Position measurements occur when the particle whose position is to be measured scatters from a detector. The scattering is inelastic: energy is not conserved in the particle and the detector is activated by the energy that the particle gives up as it scatters. In the common position-measuring devicescloud chambers, scintillation counters, and photographic platesthe relevant scattering interaction is the same. The particle scatters from a target in the detector, and the energy that is given up by the particle causes the detector to ionize. The devices differ in how they collect or register the ions; but in each case the presence of the particle is registered only if the appropriate ionization interaction occurs. So, at best, the probability of a count in the detecting device is equal to the probability of the designated ionization interaction.
Matters may be much worse. General background radiation may produce ionization when no particle is present. Conversely, the ion-collecting procedure may be inefficient and ions that are produced by the scattered particle may fail to register. Photographic emulsions are highly efficient in this sense; efficiencies in some cases are greater than 98 per cent. But other devices are not so good. In principle it is possible to correct for these effects in calculating probabilities. For simplicity I shall consider only devices that are ideally efficientthat is, I shall assume that all and only ions that are produced by the scattered particle are collected and counted.
I have urged that a real detector cannot respond to the mere presence of a particle, but will react only if the particle transfers energy to it. If the amplification process is maximally efficient so that the counter registers just in case the appropriate energy is transferred, then a particle will register in the detector if and only if the appropriate energy interchange occurs. This could create a serious consistency problem for the theory: a particle will be found at r in a position measurement just in case a detector located at r undergoes some specific energy interaction with the particle. As we have been discussing, the probability of the first event is supposed to be |ψ(r 2d3r. But the probability of the second is calculated in a quite different way, by the use of the methods of scattering theory. Quantum mechanics is consistent only if the two probabilities are equal, or approximately so. Otherwise |ψ(r 2 will not give the probability that the system will be found at r in a real physical measurement.
In fact this is stronger than necessary, for we are not interested in the absolute values of the probabilities, but merely in their relative values. Consider, for example, the photographic plate, which is the device best suited for determining densities of particles at fairly well-defined positions. In a photographic plate we are not concerned that the number of spots on the plate should record the actual number of particles, but rather that the pattern on the plate should reflect the distribution of particles. This requires establishing not an equality, but merely a proportionality:
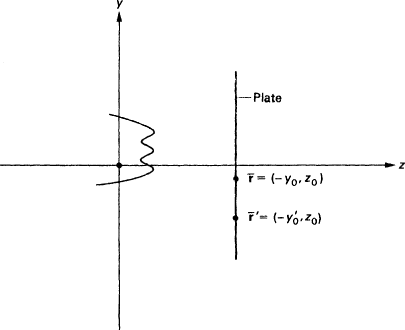
Fig 9.3. Origin located at source of wave
For a general justification, (9.1) should be true for any state function ψ for which the problem is well defined. For simplicity I will treat a two-dimensional example, in which a row of detectors is arrayed in a line perpendicular to the z axis. We may think of the detectors as the active elements in a photographic plate. In this case ψ(r, t) should be arbitrary in shape, except that at t = 0 it will be located entirely to the left of the plate (see Figure 9.3). It is easiest to establish (9.1) not in its immediate form, but rather by inverting to get

Thus, the aim is to show that the ratio in (9.2) is a constant independent of r. A shift of coordinates will help. We think of fixing the centre of the wave and varying the location of
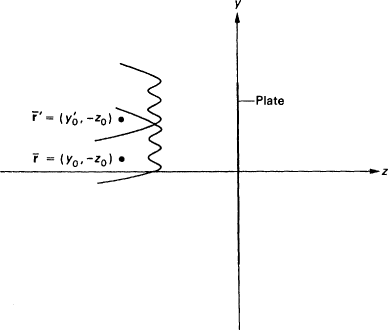
Fig 9.4. Origin located at detector
the detector across the plate (Figure 9.3). But the same effect is achieved by fixing the location of the detector and varying the centre of the wave (Figure 9.4). Looked at in this way, the consistency result can be seen as a trivial consequence of a fundamental theorem of scattering theory. This theorem states that the scattering cross section, both total and differential, is a constant independent of the shape or location of the incoming wave packet. The total scattering cross section is essentially the ratio of the total probability for the particle to be scattered, divided by the probability for crossing the detector. Roughly, the theorem assures that the probability of scattering from the detector for a wave centred at r divided by the probability for being at the detector, is a constant independent of r 0 . This is just what is required by (9.2).
There is one difficulty. Standard textbook proofs of this theorem do not establish the result for arbitrary waves, but only for wave packets that have a narrow spread in the direction of the momentum. This is not enough to ensure consistency. In a previous paper I have calculated (9.2) directly and shown it to hold for arbitrary initial states.20
I have been urging that the interpretation of quantum mechanics should be seen entirely in terms of transition probabilities. Where no transitions occur, ψ must remain uninterpreted, or have only a subjunctive interpretation: if the system were subject to a perturbing potential of the right sort, the probability for a transition into statewould be . This makes the theory considerably less picturesque. We think in terms of where our microsystems are located, and all our instincts lead us to treat these locations as real. It is a difficult matter to give up these instincts; but we know from cases like the two-slit experiment that we must, if our talk is to be coherent.
We should consider one more example in detail, to see exactly how much of our reasoning in quantum mechanics relies on picturing the positions of quantum systems realistically, and what further steps we must take if we are going to reject this picture. Dipole radiation is one of the clearest examples where position seems to count. Recall from Essay 7 that the atoms in a laser behave very much like classical electron oscillators. I will use the treatment in Sargent, Scully, and Lamb to make it easy for the reader to follow, but the basic approach is quite old. Dipole radiation is one of the very first situations to which Schroedinger applied his new wave mechanics. Sargent, Scully and Lamb tell us:
It is supposed that quantum electrons in atoms effectively behave like charges subject to the forced, damped oscillation of an applied electromagnetic field. It is not [at] all obvious that bound electrons behave in this way. Nevertheless, the average charge distribution does oscillate, as can be understood by the following simple argument. We know the probability density for the electron at any time, for this is given by the electron wave function as ψ*(r, t (r, t). Hence, the effective charge density is
For example, consider a hydrogen atom initially in its ground state with [a] spherical distribution . . . Here the average electron charge is concentrated at the center of the sphere. Application of an electric field forces this distribution to shift with respect to the positively charged nucleus . . . Subsequent removal of the field then causes the charged sphere to oscillate back and forth across the nucleus because of Coulomb attraction. This oscillating dipole acts something like a charge on a spring.21
Fig 9.5. Oscillating charge distribution in a hydrogen atom (Source: Siegman, Lasers).
Consider as a concrete example a hydrogen atom in its ground state (the 1s state, which I shall designate by U a (r)). If the atom is subject to an external electric field, it will evolve into a superposition of excited and de-excited states,
as we have seen before. (Here I will take the excited state to be the 2p state, with m = 0, designated by U b (r).) So at t the state of the hydrogen atom in an electric field is
If we chart the charge density e|ψ(r, t 2 at intervals ![]() apart,
we see from Figure 9.5 that the charge distribution moves in space like a
linear dipole, and hence has a dipole moment.22 The dipole
moment for the atom is given by
apart,
we see from Figure 9.5 that the charge distribution moves in space like a
linear dipole, and hence has a dipole moment.22 The dipole
moment for the atom is given by
The brackets, ⟨er⟩, on the left indicate that we are taking the quantum mechanical expectation. As Sargent, Scully, and Lamb say, The expectation value of the electric dipole moment ⟨er⟩ is given by the average value of er with respect to this probability density [the density ψ*(r (r)].23 The location of the electron is thus given a highly realistic treatment here: the dipole moment at a time t is characterized in terms of the average position of the electron at t.
Classically an oscillating dipole will radiate energy. The quantum analogue of this dipole radiation is central to the Lamb theory of the laser. In a laser an external field applied to the cavity induces a dipole moment in the atoms in the lasing medium. The calculation is more complicated, but the idea is the same as in the case of the hydrogen atom that we have just looked at. Summing each of the microscopic dipole moments gives the macroscopic moment, or polarization, of the medium. This in turn acts as a source in Maxwell's equations. A condition of self-consistency then requires that the assumed field must equal the reaction field. Setting the two equal, we can derive a full set of equations to describe oscillation in a laser.
I have two comments about the realistic use of electron position in the Lamb theory. The first is fairly instrumentalist in tone. The principal equations we derive in this kind of treatment are rate equations either for the photons or for the atoms. These are equations for the time rate of change of the number of photons or for the occupation numbers of the various atomic levels: that is, they are equations for transition probabilities. As with scattering or simple decay, these probabilities are completely classical. The equations are just the ones that should result if the atoms genuinely make transitions from one state to another. Louisell, for instance, in his discussion of Lamb's treatment derives an equation for the occupation number N a , of the excited state:
He tells us:
The physical meaning of these equations should be quite
clear. Equation (8.3.21) gives the net rate of change at which atoms are
entering and leaving state |a⟩. The R a
term gives the rate at which atoms are being pumped into level |a⟩.
The −Γ a N a
term represents the incoherent decay of atoms from level |a⟩ to
lower levels. We could also add a term +W ab N b
to represent incoherent transitions from |b⟩ to |a⟩,
but we omit this for simplicity. The ![]() is
the lifetime of the atom in level |a⟩ in the absence of [a]
driving field. These first terms are incoherent since they contain no phase
information. . .
is
the lifetime of the atom in level |a⟩ in the absence of [a]
driving field. These first terms are incoherent since they contain no phase
information. . .
The last term i(PE*−P*E) represents the net induced population change in level |a⟩ due to the presence of a driving field.24
What is important to notice is that the change in the number of excited atoms is just equal to the number of atoms going into the excited state minus the number going out. There are no terms reflecting interference between the excited and the de-excited states.
Recall that in Essay 6 we showed that the exponential decay law can be derived by a Markov approximation, which assumes that there is no correlation among the reservoir variables. Exactly the same device is used to eliminate the non-classical interference terms here. For example, in deriving the photon rate equation, H. Haken remarks:
We shall neglect all terms with ![]() .
This can be justified as follows. . . The phases of the b*'s
fluctuate. As long as no phase locking occurs the phase fluctuations of the
different b's are uncorrelated. The mixed terms on the right hand side
of 134 [i.e. the interference terms in the photon rate equation] vanish if an
average over the phases is taken.25
.
This can be justified as follows. . . The phases of the b*'s
fluctuate. As long as no phase locking occurs the phase fluctuations of the
different b's are uncorrelated. The mixed terms on the right hand side
of 134 [i.e. the interference terms in the photon rate equation] vanish if an
average over the phases is taken.25
The classical character of the rate equations leaves us in a peculiar position. On the one hand, the superposition of excited and de-excited states is essential to the theoretical account. There is no dipole moment without the superpositionthe charge density e|ψ(r 2 does not oscillate in space in either the excited state alone or in the de-excited state alone. Without the dipole moments, there is no macroscopic polarization produced by the medium, and hence no grounds for the self-consistency equations with which Lamb's derivations begin. On the other hand, the classical character of the rate equations suggests that the atoms genuinely change their states. If so, this is just like the picture I have sketched for simple decay cases: the atom makes a transition, Schroedinger evolution stops and reduction of the wave packet takes over. The very formalism that allows us to predict that this will occur does not apply throughout the entire process.
This leads me to suppose that the whole account is an explanatory fiction, including the oscillating dipoles, whose role is merely to motivate us to write down the correct starting equation. The account is best seen as a simulacrum explanation. The less radical response is to notice that Lamb and others describe e|ψ(r 2 as the charge distribution. In this very simple case, we need not see it as a probability distribution at all, but as a genuine charge density in space. This of course will not do as a general interpretation of ψ*ψ. (Generally ψ must be taken as a function in a phase space. Where more than one electron is involved, ψ will be a function of the position of all of the electrons; and in general ψ*ψ in the phase space will not reduce to a simple distribution in real space for the charges involved.) But for any case where we want to claim that the dipole moment arises from a genuine oscillation, this must be possible. Otherwise the correct way to think about the process is not in terms of probabilities at all, but rather this way: the field produced by the atoms contributes to the macroscopic polarization. ⟨er⟩ is the quantity in the atoms responsible for the micro-polarization it produces. We learn to calculate this quantity by taking e|ψ(r 2, and this calculation is formally analogous to computing a moment or an average. But the analogy is purely formal. e|ψ(r 2 is a quantity which gives rise to polarization in the field; it has no probabilistic interpretation. This way of viewing expectations is not special to this case. Whenever an expectation is given a real physical role, it must be stripped of its probabilistic interpretation. Otherwise, how could it do its job? ⟨er⟩ certainly is not the average of actual possessed positions, since electrons in general do not possess positions. The conventional alternative would have it be the average of positions which would be found on measurement. But that average can hardly contribute to the macroscopic polarization in the unmeasured cavity.
In this section I have argued that two independent reasons suggest interpreting quantum mechanics by transition probabilities and not by position probabilities or probabilities for other values of classic dynamic quantities. First, transition events play a causal role in the theory which is not matched by the actual positions, momenta, etc. of quantum systems. The second is that transition probabilities are classical, and so too are their event spaces, so there is no need for either a special logic or a special probability. Both of these arguments suppose that transitions are events which actually occur: sometime, indeterministically, the system does indeed change its state. This is the view that Max Born defended throughout his life. We find a modern statement of it in the text of David Bohm:
We conclude that |C m |2 yields the probability that a transition has taken place from the sth to the mth eigenstate of H since the time t = t 0 . Even though the C m 's change continuously at a rate determined by Schrdinger's equation and by the boundary conditions at t = t 0 , the system actually undergoes a discontinuous and indivisible transition from one state to the other. The existence of this transition could be demonstrated, for example, if the perturbing potential were turned off a short time after t = t while the C m 's were still very small. If this experiment were done many times in succession, it would be found that the system was always left in some eigenstate of H In the overwhelming majority of cases, the system would be left in its original state, but in a number of cases, proportional to |C m |2, the system would be left in the mth state. Thus, the perturbing potential must be thought of as causing indivisible transitions to other eigenstates of H 0 .26
But this view is not uncontroversial. To see the alternative views, consider radioactive decay. There are two ways to look at it, one suggested by the old quantum theory, the other by the new quantum theory. The story told by the old quantum theory is just the one with which most of us are familiar and which I adopt, following Bohm. First, radioactive decay is indeterministic; second, the activity decreases exponentially in time; and third, it produces a chemical change in the radioactive elements. Henri Becquerel reported the first observations of radioactivity from uranium in a series of three papers in 1886. Marie Curie did a systematic study of uranium and thorium beginning in 1898, for which she and Pierre Curie shared a Nobel prize with Becquerel. But it was not until the work of Rutherford and Soddy in 1902 that these three important facts about radioactivity were recognized. The first and second facts come together. The probability for the material to remain in its excited state decreases exponentially in time, and no external influence can affect this probability, either to increase it or to decrease it. Rutherford and Soddy report:
It will be shown later that the radioactivity of the emanation produced by thorium compounds decays geometrically with the time under all conditions, and is not affected by the most drastic chemical and physical treatment. The same has been shown by one of us to hold for the excited radioactivity produced by the thorium emanation.
This decays at the same rate whether on the wire on which it is originally deposited, or in the solution of hydrochloric or nitric acid. The excited radioactivity produced by the radium emanation appears analogous.27
The third fact is the one of relevance to us. From
Contrast this with the new-quantum-theory story. This is the story we read from the formalism of the developed mathematical theory. On this story nothing happens. In atomic decay the atom begins in its excited state and the field has no photons in it. Over time the composite atom-plus-field evolves continuously under the Schroedinger equation into a superposition. In one component of the superposition the atom is still in the excited state and there are no photons present; in the other, the atom is de-excited and the field contains one photon of the appropriate frequency. The atom is neither in its outer orbit nor in its inner orbit, and the photon is neither there in the field travelling away from the atom with the speed of light, nor absent. Over time the probability to be found in the state with an excited atom and no photons decays exponentially. In the limit as t → ∞, the probability goes to zero. But only as t → ∞! On the new-quantum-theory story, never, at any finite time, does an atom emit radiation. Contrary to Bohr's picture, the system may never be regarded as passing from one state to another.
The situation with scattering is no better. A particle with a fixed direction and a fixed energy bombards a target and is scattered. The state of the scattered particle is represented by an outgoing spherical wave (see Figure 9.6 in the Appendix). After scattering the particle travels in no fixed direction; its outgoing state is a superposition of momentum states in all directions. We may circle the target with a ring of detectors. But as we saw in discussing the problem of preparation, this is of no help. If we look at the detectors, we will find the particle recorded at one and only one of them. We are then cast into a superposition; each component self sees the count at a different detector. It is no wonder that von Neumann says that here at least reduction of the wave packet occurs. But his reduction comes too late. Even without the detectors, the particle must be travelling one way or another far away from the target.
So on my view, as in the old quantum theory, reduction of the wave packet occurs in a variety of situations, and independent of measurement. Since I have said that super-positions and mixtures make different statistical predictions, this claim ought to be subject to test. But direct statistical test will not be easy. For example, to distinguish the two in the case of atomic decay, we would have to do a correlation experiment on both the atom and its associated photon, and we would have to measure some observable which did not commute with either the energy levels of the atom or the modes of the perturbed field. (This is laid out formally, in Superposition and Macroscopic Observation.) But these kinds of measurements are generally inaccessible to us. That is what the work of Daneri, Loinger, and Prosperi exploits. Still, with ingenuity, we might be able to expose the effects of interference in some more subtle way.
P. H. Eberhard has proposed some experiments which attempt to do so.31 Vandana Shiva proposes a test as well.32 Not all tests for interferences will be relevant, of course, for reductions occur, but not all of the time. Otherwise there would be no interference pattern on the screen in the two-slit experiment, and the bonding energy of benzene would be different. But there is one experiment that Eberhard proposes which I would count as crucial. This is a test to look for reduction of the wave packet in one of the very cases we have been consideringin scattering. I will discuss Eberhard's experiment in the Appendix.
3. How the Measurement Problem Is an Artefact of the Mathematics
Von Neumann claimed that reduction of the wave packet occurs when a measurement is made. But it also occurs when a quantum system is prepared in an eigenstate, when one particle scatters from another, when a radioactive nucleus disintegrates, and in a large number of other transition processes as well. That is the lesson of the last two sections. Reductions of the wave packet go on all of the time, in a wide variety of circumstances. There is nothing peculiar about measurement, and there is no special role for consciousness in quantum mechanics.
This is a step forward. The measurement problem has disappeared. But it seems that another has replaced it. Two kinds of evolution are still postulated: Schroedinger evolution and reduction of the wave packet. The latter is not restricted to measurement type situations, but when does it occur? What features determine when a system will evolve in accord with the Schroedinger equation and when its wave packet will be reduced? I call this problem the characterization problem. I am going to argue that it is no real problem: it arises because we mistakenly take the mathematical formulation of the theory too seriously. But first we should look at a more conventional kind of answer.
There is one solution to the characterization problem that
is suggested by the formal Schroedinger attempts to minimize interference
terms: reduction of the wave packet occurs when and only when the system in
question interacts with another which has a very large number of independent
degrees of freedom. Recall the derivations of exponential decay discussed
in Essay 6. In the WeisskopfWigner treatment we assume that the atom couples
to a quasi-continuum of modes of the electromagnetic field. If instead it
coupled to only one, or a few, the probability would not decay in time, but
would oscillate back and forth forever between the excited and de-excited
states. This is called Rabi-flopping. I mentioned before the discussion by P.
C. W. Davies.33 Davies's derivation shows clearly how
increasing the number of degrees of freedom eliminates the interference terms
and transforms the Rabi oscillation into an exponential decay. Similarly, the
DaneriLoingerProsperi proof that I described in Section 1 of this chapter
relies on the large number of degrees of freedom of the measuring apparatus.
This is the ground for their assumption (corresponding to assumption A 2
in Superposition and Macroscopic Observation) that there will be no
correlation in time between systems originating in different microstates of the
same macro-observable. This is exactly analogous to Haken's assumption, quoted
in the last section, that ![]() ,
and b λ are uncorrelated over time, and it plays an
analogous role. For that is just the assumption that allows Haken to eliminate the
interference terms for the photons and to derive the classical rate equations.
,
and b λ are uncorrelated over time, and it plays an
analogous role. For that is just the assumption that allows Haken to eliminate the
interference terms for the photons and to derive the classical rate equations.
The most general proofs of this sort I know are in derivations of the quantum statistical master equation, an equation analogous to the evolution equations of classical statistical mechanics. The Markov treatment of radioactive decay from Essay 6 is a special case of this kind of derivation. In deriving the master equation the quantum system is coupled to a reservoir. In theory the two should evolve into a superposition in the composite space; but the Markov approximation removes the interference terms and decouples the systems. Again the Markov approximation, which treats the observation time as infinitely long, is justified by the large number of independent degrees of freedom in the reservoir, which gives rise to short correlation times there.
There are two difficulties with these sorts of proofs as a way of solving the characterization problem. The first is practical. It is a difficulty shared with the approach I shall defend in the end. Reduction of the wave packet, I have argued, takes place in a wide variety of circumstances. But treatments of the sort I have been describing have been developed for only a small number of cases, and, with respect to measurement in particular, treatments like that of Daneri, Loinger, and Prosperi are very abstract and diagrammatic. They do not treat any real measurement processes in detail.
The second difficulty is one in principle. Even if treatments like these can be extended to cover more cases, they do not in fact solve the characterization problem. That problem arises because we postulate two different kinds of evolution in nature and we look for a physical characteristic that determines when one occurs rather than the other. Unfortunately the characteristic we discover from these proofs holds only in models. It is not a characteristic of real situations. To eliminate the interference the number of relevant degrees of freedom must be infinite, or correlatively, the correlation time zero. In reality the number of degrees of freedom is always finite, and the correlation times are always positive.
Conceivably one could take the opposite tack, and urge that all real systems have infinitely many degrees of freedom.
That leaves no ground to distinguish the two kinds of evolution either. The fact that this view about real systems is intrinsically neither more nor less plausible than the first suggests that the concept relevant number of degrees of freedom is one that applies only in models and not in reality. If we are to apply it to reality I think we had best admit that real systems always have a finite number of degrees of freedom.
A real system may be very largelarge enough to model it as having infinitely many degrees of freedom, or zero time correlationsbut this does not solve the characterization problem. That problem requires one to separate two very different kinds of change, and size does not neatly divide the world in pieces. This is a familiar objection: if bigness matters, how big is big enough? Exactly when is a system big enough for nature to think it is infinite?
Sheer size cannot solve the characterization problem as I have laid it out. But I now think that what I have laid out is a pseudo-problem. The characterization problem is an artefact of the mathematics. There is no real problem because there are not two different kinds of evolution in quantum mechanics. There are evolutions that are correctly described by the Schroedinger equation, and there are evolutions that are correctly described by something like von Neumann's projection postulate. But these are not different kinds in any physically relevant sense. We think they are because of the way we write the theory.
I have come to see this by looking at theoretical frame-works recently developed in quantum statistical mechanics. (E. B. Davies's Quantum Theory of Open Systems34 probably represents the best abstract formalization.) The point is simple and does not depend on details of the statistical theory. Von Neumann said there were two kinds of evolutions. He wrote down two very different looking equations. The framework he provides is not a convenient one for studying dissipative systems, like lasers or radiating atoms. As we have seen, the Schroedinger equation is not well able to handle these; neither is the simple projection postulate given by von Neumann. Quantum statistical mechanics has developed a more abstract formalism, better suited to these kinds of problems. This formalism writes down only one evolution equation; the Schroedinger equation and the projection postulate are both special cases of this single equation.
The evolution prescribed in the quantum statistical formalism is much like Schroedinger evolution, but with one central difference: the evolution operators for quantum statistical processes form a dynamical semi-group rather than a dynamical group. The essential difference between a group and a semi-group is that the semi-group lacks inverses and can thereby give rise to motions which are irreversible. For instance, the radiating atom will decay irreversibly instead of oscillating forever back and forth as it would in Rabi-flopping. Correlatively, the quantum statistical equation for evolution looks in abstract like a Schroedinger equation, except that the operation that governs it need not be represented by a unitary operator. A unitary operator is one whose adjoint equals its inverse. The effect of this is to preserve the lengths of vectors and the angles between them. There are other mathematical features associated with unitarity as well, but in the end they all serve to block reduction of the wave packet. So it is not surprising that the more general quantum statistical framework does not require a unitary operator for evolution.
From this new point of view there are not two kinds of evolution described by two kinds of equation. The new formalism writes down only one equation that governs every system. Is this too speedy a solution to the characterization problem? Perhaps there is only one equation, but are there not in reality two kinds of evolution? We may agree that Schroedinger's equation and reduction of the wave packet are special cases of the quantum statistical law: a Schroedinger-like equation appears when a unitary operator is employed; a reduction of the wave packet when there is a non-unitary operator. Does this not immediately show how to reconstruct the characterization problem? Some situations are described by a unitary operator and others by a non-unitary operator. What physical difference corresponds to this?
There is a simple, immediate reply, and I think it is the right reply, although we cannot accept it without considering some questions about determinism. The reply is that no physical difference need explain why a unitary operator is used in one situation and why a non-unitary one is required in another. Unitarity is a useful, perhaps fundamental, characteristic of operators. That does not mean that it represents a physical characteristic to be found in the real world. We are misled if we take all mathematics too seriously. Not every significant mathematical distinction marks a physical distinction in the things represented. Unitarity is a case in point.
How, we may still ask, does nature know in a given situation whether to evolve the system in a unitary or a non-unitary way? That is the wrong question. The right, but trite, question is only, How does nature know how to evolve the system? Well, nature will evolve the system as the quantum statistical equation dictates. It will look at the forces and configurations and at the energies these give rise to, and will do what the equation requires when those energies obtain. Imagine that nature uses our methods of representation. It looks at the energies, writes down the operator that represents those energies, solves the quantum statistical equation, and finally produces the new state that the equation demands. Sometimes a unitary operator will be written down, sometimes not.
I reject the question, How does nature know in a given situation whether to use a unitary or non-unitary operator? That question presupposes that nature first looks at the energies to see if the operator will be unitary or not, and then looks to see which particular operator of the designated kind must be written down. But there is no need for the middle step. The rules that assign operators to energies need not first choose the kind of operator before choosing the operator. They just choose the operator.
I write as if unitarity has no physical significance at all. It has only mathematical interest. Is this so? No, because unitarity is just the characteristic that precludes reduction of the wave packet; and, as we have seen, reduction of the wave packet is indeterministic, whereas Schroedinger evolution is deterministic. This, according to the quantum theory, is a genuine physical difference. (Deterministic motions are continuous; indeterministic are discontinuous.) I do not want to deny that there is this physical difference; but rather to deny that there must be some general fact about the energies that accounts for it. There need be no general characteristic true of situations in which the evolution is deterministic, and false when the evolution is indeterministic. The energies that obtain in a given situation determine how the system will evolve. Once the energies are fixed, that fixes whether the evolution is deterministic or indeterministic. No further physical facts are needed.
If this interpretation is adopted, determinism becomes for quantum mechanics a genuine but fortuitous physical characteristic. I call it fortuitous by analogy with Aristotle's meeting in the market place. In the Physics, Book II, Chapter 5, Aristotle imagines a chance encounter between two men. Each man goes to the market place for motives of his own. They meet there by accident. The meeting is fortuitous because the scheme of motives and capacities explains the presence of each man separately, but it does not explain their meeting. This does not mean that the meeting was not a genuine physical occurrence; nor that anything happened in the market place that could not be predicted from the explanatory factors at handin this case the motions and capacities of the individuals. It means only that meetings as meetings have no characteristic cause in the scheme of explanation at hand. This does not show that there is some mistake in the scheme, or that it is incomplete. We may be very interested in meetings, or for that matter, determinism, or the money cycle; but this does not guarantee that these features will have characteristic causes. A theory is not inadequate just because it does not find causes for all the things to which we attend. It can be faulted only if it fails to describe causes that nature supplies.
Professor Florence Leibowitz suggests another way to understand the place of determinism in the interpretation I propose. She says, Your claim about unitarity is in effect an assertion that indeterministic evolutions ought to be seen as primitive for quantum mechanics, in the sense that behaving according to the law of inertia is a primitive for post-scholastic mechanics.35 The conventional von Neumann-based view of evolution sees deterministic evolution as the natural situation, Leibowitz suggests. Indeterministic evolution is seen as a departure from what would naturally occur, and hence requires a causean interaction with a reservoir, perhaps, or with a conscious observer. But on my understanding of the quantum statistical formalism, indeterministic motions are natural too. They are not perturbations, and hence do not require causes. This is exactly analogous to what happens to inertial motion in the shift from Scholastic to Newtonian mechanics. For the Scholastic, continued motion in a straight line was a perturbation and a cause was required for it. In the Newtonian scheme the continued motion is natural or, as Leibowitz says, primitive. Likewise quantum mechanics does not need a physical property to which unitarity corresponds: even if there were such a property, Leibowitz points out, it would not have any explanatory work to do.
Throughout these essays I have urged that causality is a clue to what properties are real. Not all predicates that play a significant role in a theory pick out properties that are real for that theory. Many, for example, represent only properties in models, characteristics that allow the derivation of sound phenomenological laws, but which themselves play no role in the causal processes described by those laws. Unitarity is a different kind of example.
To understand what role unitarity plays in the theory, first look at another property that evolution operators may have: invariance under some group of transformations. In Schroedinger theory, the Hamiltonian describes the energies in the situation and thereby determines the evolution operator. Whenever the Hamiltonian is invariant under a group of transformations, there will be some constant of the motion which exhibits degeneracies; that is, different, incompatible states will have the same value for that quantity. Rotational invariance is a simple example. Rotational invariance in a Hamiltonian corresponds to spherical symmetry in the energies and forces represented by that Hamiltonian. The spherical symmetry produces degeneracies in the energy levels, and disturbing the symmetry eliminates the degeneracies. If a small non-symmetric field is added, a number of closely spaced lines will appear in the spectroscope where before there was only one. The rotational invariance of the Hamiltonian is a sign of a genuine physical characteristic of the situation.
Unitarity is different. We are often interested in whether the motion in a given kind of situation will be deterministic or indeterministic. There is a long way to find this out: consider the energies in the situation; write down the operator that represents them; solve the quantum statistical equation; and look to see if the consequent change is continuous. This is cumbersome. We would like some way to read from the operator itself whether the solutions will be continuous or not. Unitarity is a mark we can use, and it is one of the strengths of the particular mathematical structure we have that it gives us such a mark. Unitarity and rotational invariance are both significant features of the evolution operator, features that we single out for attention. But they play very different roles. Rotational invariance marks a genuine characteristic of the energy, a characteristic that is postulated as the source of a variety of physical consequences; unitarity provides an important mathematical convenience. To demand a physical correlate of unitarity is to misunderstand what functions it serves in the quantum theory.
I do not want to insist that unitarity does not represent a genuine property, but rather that the failure to find such a property is not a conceptual problem for the theory. Larry Laudan's description of a conceptual problem fits here. Laudan says, Such problems arise for a theory, T, . . . when T makes assumptions about the world that run counter to . . . prevailing metaphysical assumptions.36 Under von Neumann's proposal that quantum systems evolve under two distinct laws, some feature was required to signal which law should operate where. No physical characteristic could be found to serve, and the theory seemed driven to metaphysically
203
suspicious characteristicsfictional properties like infinite degrees of freedom or zero correlation times, or, even worse, interaction with conscious observers. But if the quantum statistical formalism can be made to work, no such property is required and the theory will not run counter to the prevailing metaphysical assumptions' that neither sheer size nor consciousness should matter to physics.
The if here presents an important condition. The comments of Jeremy Butterfield about my proposal seem to me right. Butterfield says,
Quantum statistical mechanics has provided a general theory of evolution of quantum states (pure and mixed) that encompasses [von Neumann's] two sorts of evolution, and many others, as special cases. Nor is this just a mathematical umbrella. It allows us to set up detailed models of phenomena that cannot be treated easily, if at all with the traditional formalism's two sorts of evolution.37
Quantum optics is one place these detailed models have been developed, especially in the study of lasers. But we have seen that a broad range of cases make trouble for the traditional Schroedinger accountscattering, for example, or any situation in which pure states are prepared, and finally the issue that started us offmeasurement. Much later Butterfield continues:
I do not want to pour cold water on this programme [of Cartwright's]; I find it very attractive. But I want to stress that it is a programme, not a fait accompli. To succeed with it, we need to provide detailed analyses of measurement situations, showing that the right mixtures are forthcoming. We need not of course cover all measurement situations, but we need to make it plausible that the right mixtures are generally obtained. (And here generally need not mean universally; it is the pervasiveness, not necessarily universality, of definite values that needs to be explained.) Only when we have such detailed analyses will the measurement problem be laid to rest.38
Butterfield gives good directions for what to do next.
I recommended the book of E. B. Davies as a good source for finding out more about the quantum statistical approach.
I should mention that Davies himself does not use the formalism in the way that I urge; for he is at pains to embed the non-unitary evolutions he studies into a Schroedinger evolution on a larger system. This goes along with his suggestion that non-unitarity is a mark of an open system, one which is in interaction with another. Open systems are presumably parts of larger closed systems, and these in Davies's account always undergo unitary change. I think this view is mistaken, for the reasons I have been urging throughout this essay. If the wave packet is not reduced on the larger system, it is not in fact reduced on the smaller either. The behaviour of the smaller system at best looks as if a reduction has occurred, and that is not good enough to account for measurements or for preparations.
I have been urging that, if the quantum statistical programme can work, the measurement problem becomes a pseudo-problem. But other, related, problems remain. These are the problems of how to pick the right operators, unitary or no, to represent a given physical situation. This is the piece by piece work of everyday physics, and it is good to have our philosophical attentions focused on it again. This is what on-going physics is about, and it knows no general procedure. In quantum mechanics the correspondence principle tells us to work by analogy with classical mechanics, but the helpfulness of this suggestion soon runs out. We carry on by using our physical intuitions, analogies we see with other cases, specializations of more general considerations, and so forth. Sometimes we even choose the models we do because the functions we write down are ones we can solve. As Merzbacher remarks about the Schroedinger equation:
Quantum dynamics contains no general prescription for the construction of the operator H whose existence it asserts. The Hamiltonian operator must be found on the basis of experience, using the clues provided by the classical description, if one is available. Physical insight is required to make a judicious choice of the operators to be used in the description of the system . . . and to construct the Hamiltonian in terms of these variables.39
As I argued in Essays 7 and 8, not bridge principles, but physical insights, are required to choose the right operators. But at least the quantum statistical programme offers hope that this mundane, though difficult, job of physics is all that there is to the measurement problem.
Appendix; An Experiment to Test Reduction of the Wave Packet
In 1972 P. H. Eberhard considered non-unitary theories of the kind I endorse here and proposed four types of tests for them. I shall discuss in detail his tests involving the optical theorem of scattering theory, since this is the case I understand best, and it is a case that fits nicely with the discussion earlier in this essay. Eberhard tells us, about the theory he discusses, Our non-unitary theory resembles the description of quantic systems in interaction with a measurement apparatus, but no apparatus is involved in the physical processes that our theory is applied to.40 Eberhard calls theories that respect unitarity class-A theories. He will be concerned with a particular class of non-unitary theoriesclass-B theories. These are theories which model change in quantum systems on what happens in a complete measurement. Specifically, for an observable M = Σm|φ m ⟩⟨φ m |, a B-type interaction takes the state D into D′:
B-type theories are thus exactly the kind of theory I have urged, in which transitions genuinely occur into eigenstates , and the final state for the ensemble is a classical mixture in which the φ m do not interfere.
Eberhard tests type-B theories with the optical theorem. He tells us,
The optical theorem is derived from the principle that the wave scattered in the forward direction interferes with the incident wave in such a way as to conserve probabilities. If the forward scattering contained a mixture, i.e., non-interfering components, the test of the
optical theorem would fail. That test involves measurements of the differential cross section in the forward direction, including the interference region between Coulomb and strong interaction scatterings. The results can then be compared to the measurements of the total cross section.41
Eberhard looks at elastic scattering in a π−p interaction at 1.015, 1.527 and 2.004 GeV. The results agree with the prediction of the optical theorem within 3%, when averaged over the three momenta.42 This agreement is good enough. If Eberhard's analysis is correct, class-B theories are ruled out for scattering interactions, and if they do not hold for scattering, they are not very plausible anywhere.
Fig 9.6. Scattering from a stationary target
The optical theorem is an obvious place to look for a test of non-unitary evolution. Consider a typical textbook presentation of the formal theory of scattering. I use Eugen Merzbacher's Quantum Mechanics. Merzbacher tells us The scattering matrix owes its central importance to the fact that it is unitary43 and later From the unitary property of the scattering matrix, we can derive an important theorem
for the scattering amplitudes44 the optical theorem. Nevertheless the optical theorem does not rule out class-B theories. The optical theorem, I will argue, holds good in just the kind of class-B theory I have described for scattering.
In the case of elastic scattering, where the bombarding particle neither loses nor gains energy, the asymptotic state for large r for an outgoing particle whose initial momentum is k, is given by
This state is a superposition of the original momentum eigenstate exp(ikr) and an outgoing spherical wave 1/r exp(ikr) as in Figure 9.6. The quantity f k (r) is called the scattering amplitude. It is the imaginary part of the scattering amplitude in the forward directionImf k (0)which enters the optical theorem. As we can see from Figure 9.6, in the forward direction the original unscattered wave and the outgoing spherical wave interfere. The interference subtracts from the probability of the incoming wave in the forward direction. This is as we would expect, since the beam in the forward direction will be depleted by the particles that strike the target and are scattered.
It is easiest to calculate the interference if we switch to the formal theory of scattering. Equation (1) is the wave function version, for large r, of the Lippman-Schwinger equation:
Here the momentum states are eigenstates of the unperturbed Hamiltonian, H 0
, and it is understood that the limit α → 0 is to be taken at the
end of the calculation. The transition matrix T nk is
proportional to the scattering amplitude. We are interested in what proportion
of the beam will be travelling in the forward direction after scattering, so we
must calculate the probability ![]() .
Substituting
.
Substituting
and using the fact that
and that
we get
Now we may repeat the kind of classical argument that we considered for the two-slit experiment. A particle travelling in the forward direction after passing the target was either scattered from the target, or passed the target unscattered:
Since S and 7S are disjoint events
But equation (2) shows that this classical reasoning will not do. The first two terms in equations (2) and (3) are identical, but, as in the two-slit experiment, the quantum mechanical calculation differs from the classical one by the interference terms, which are responsible in the two-slit case for the troughs in the diffraction pattern, and in scattering for the shadow cast by the target. We see that the amount of interference depends on the imaginary part of the forward scattering amplitude.
The optical theorem relates the total cross section, σ, to Imf k (0):
The cross section, σ, measures the total probability for
209
scattering into any angle. Recall that Eberhard reported, The optical theorem is derived from the principle that the wave scattered in the forward direction interferes with the incident wave in such a way as to conserve probabilities. We can now see why this is so. The optical theorem says that the loss in the beam in the forward direction, which we have seen comes from the interference term, Im f k (0), is equal to the total number of particles scattered. Interference is thus an essential part of the optical theorem. How then can I maintain that reduction of the wave packet after scattering is consistent with the optical theorem?
The key to the answer is that one must be careful about what final states the system is supposed to enter when reduction occurs. I suggested, following Bohm, that after scattering each particle will be travelling in a specific direction, and with a specific energy. The reduction takes place into the eigenstates of momentum. The optical theorem precludes only a reduction into the pair scatteredunscattered. But the momentum probabilities already contain the interference between the incoming plane wave and the scattered spherical wave.
We can see this by looking back to the LippmanSchwinger equation. It follows from that equation (taking the limit as α → 0) that the amplitude for a system with initial momentum k at t = −∞ to have momentum k′ at t = +∞, is given by
Here I have identified this amplitude with the k, k′th element of the scattering matrix, S, as we learn we can do from the formal theory of scattering. The total amplitude is thus a superposition of the amplitude from the scattered wave plus the amplitude from the unscattered wave, so the interference between the two is present right in the momentum amplitudes. When the complex conjugate is taken, equation (2) will result as required. It is no surprise then that the optical theorem still holds for the kind of reduction I propose.
Formally, I imagine that after reduction the state of particles in the beam is given by D′:
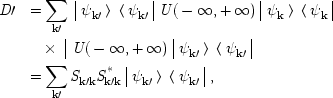
where U(t, t′) is the normal unitary evolution operator supplied by Schroedinger theory. (It is conventional to take the limits as t→∞ since the times involved before detection are very long on the microscopic scale.) Since D → D′ is a measurement-type interaction on the momentum eigenstates, the momentum probabilities after reduction will be the same as before reduction. But the optical theorem is a trivial consequence of the conservation of total probability among the momentum states. Here is where the unitarity of the scattering matrix, which Merzbacher stresses, plays its role. Because S is unitary, the probabilities to be in one or another of the momentum eigenstates sum to one
not only in the unreduced state but in the reduced state as well. This is enough to guarantee that the optical theorem holds. The proof is simple, and I shall omit it here. (It is set as exercise 19.5 in Merzbacher: Derive the optical theorem from the conservation of probability and (19.12) where equation (19.12) gives the amplitude for the k′th momentum state at t.) Thus, the optical theorem is consistent with a class-B interaction in which the wave packet is reduced into momentum eigenstates after the particle has been scattered.
What then of Eberhard's claims? To see how to reconcile what Eberhard says with the facts I have just noted, we need to look more closely at the kind of class-B theory which Eberhard considers. Eberhard notes that a non-unitary evolution like D → D′ can always be written as a sum of unitary evolutions. This gives rise to something like a hidden
211
variable theory: where we see a single physical process which appears to follow a non-unitary rule, there are in fact a mixture of different processes each manifesting a unitary Schroedinger evolution. Or, alternatively: take the final pure states produced by Eberhard's set of component unitary evolutions and wind them backwards by using the inverse of the original unitary scattering matrix. Then, the Eberhard style hidden variable theory says that, contrary to the normal assumption, the incoming state is not pure, but instead a mixture of these wound-backward states. Each state behaves exactly as the Schroedinger equation predicts. We end with a mixture, but only because we begin with one.
Even though he does not explicitly say so, Eberhard's calculations take this hidden variable theory very seriously. Eberhard's test uses two theorems from scattering theory. The first relates the differential cross-section in the forward direction to the scattering amplitude in that direction:
Using R and J as Eberhard does to refer to the real and imaginary parts of f k (0), we get Eberhard's equation (4.2).46
The second theorem is the optical theorem, which Eberhard writes as
As Eberhard remarks, R can be calculated from J, or it can be determined from the interference with Coulomb scattering. Since σ and dσ(0)/dΩ can be measured in independent experiments, a test of the optical theorem is at hand.
Let us now look to see how Eberhard turns this into a test of class-B evolutions using his earlier theorem that any non-unitary evolution of B-type is equivalent to a weighted average of unitary changes. Eberhard claims:
In a class B theory, there are pseudo-states j that correspond to weights w j and unitary matrices S j . Each unitary matrix S j corresponds to a class A theory, therefore to a σ j , to a dσ j /dΩ, to a R j (E) and to a J j (E)
212
satisfying eq. (4.1) to (4.5). The effective probability distributions are the weighted averages of those class A predictions and the effective cross sections σ and dσ/dΩ are the weighted averages of the σ j 's and of the dσ j /dΩ respectively.47
So, says Eberhard,
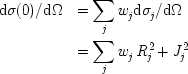
and
Using E(4.8), R2 + J2 = (Σw j R j )2 + (Σw j J j )2. But in general
So, if E(4.7) is correct, E(4.2) will be violated.
It remains to substantiate that equations E(4.7) and E(4.8) are true for class-B theories. E(4.7) is straightforward. Letting W represent the total transition rate into a solid angle dΩ, from B
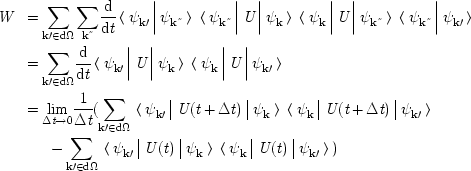
213
From Eberhard's earlier theorem that class-B evolutions are equivalent to weighted averages of unitary evolution U j ,
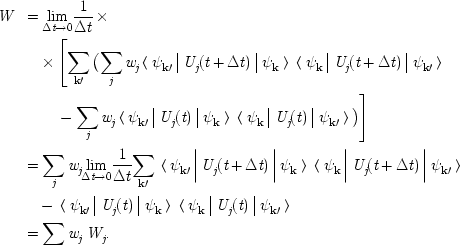
But
where ![]() is
the probability that a particle is incident on a unit area perpendicular to the
beam per unit time. Hence,
is
the probability that a particle is incident on a unit area perpendicular to the
beam per unit time. Hence,
So equation E(4.7) holds.
But what of E(4.8)? E(4.8) is justified only if we insist on an Eberhard-style
hidden variable theory. Eberhard shows that the non-unitary evolution B
can always be mathematically decomposed as an average over unitary evolutions.
The hidden variable version of the class-B theory supposes that this
mathematical decomposition corresponds to a physical reality: scattering is
really a mix of physical processes, each process governed by one of the unitary
operators, U j , which make
up the mathematical decomposition. In this case, we have a variety of different
scattering processes, each with its own scattering amplitude ![]() ,
and its own
,
and its own
214
cross-sections, σ j , and E(4.8) is a reasonable constraint on the real and imaginary parts of the scattering amplitudes.
But is this physically robust hidden variable version of a class-B theory a reasonable one from our point of view? No, it is not. For it does not solve the problem of preparation that motivated our class-B theory to begin with. Scattering interactions prepare beams in momentum eigenstates: particles which appear in a particular solid angle dΩ at one time are expectedthose very same particlesto be travelling in exactly the same solid angle later, unless they are interfered with. So we look for physical processes whose end-states are eigenstates of momentum. But the end-states of the processes U j are nothing like that.
From Eberhard's decomposition proof there are as many hidden processes as there are dimensions to the space needed to treat the system. In the case of scattering, a quasi-continuum of states is required. Each hidden process turns out to be itself a scattering-type interaction. The end-state of the first hidden process is just the normal outgoing spherical wave of conventional scattering theory. This conventional state will have the weight 1/n, when n is the dimension of the space. So, too, will each of the remaining states. The end-state of the second process will be much like the first, except that the amplitude of the second momentum eigenstate will be rotated by 180. Similarly, the third process rotates the amplitude of the third momentum eigenstate by 180; the fourth rotates the fourth amplitude; and so on. In average, the effect of these rotations is to cancel the interference among the momentum states and to produce a final mixture whose statistical predictions are just like those from a mixture of momentum states. But in truth, when the hidden variable account is taken seriously, the final state is a mixture of almost spherical waves, each itself a superposition of momentum eigenstates; and it is not in fact a mixture of momentum eigenstates as we had hoped. But if we do not take the hidden variable theory seriously and give a physical interpretation to the decomposition into unitary processes, there is no ground for equations E(4.8)a and E(4.8)b, and the optical theorem is no test of B-type evolutions.
The Eberhard inequality E.I. is based on equations E(4.8)a and E(4.8)b, which I claim are plausible for an
Eberhardstyle hidden variable theory, but which do not hold for a class-B
theory which takes each incoming particle into a momentum eigenstate. We should
now confirm this last claim. The process which produces a mixture of momentum
eigenstates is itself composed of a mixture of processes, each of which
produces one or another of the eigenstates of momentum as its final product.
(Note: each of these processes is non-unitary, because it shrinks the
vector. Nor can we reconstruct it as a unitary evolution by taking the
shrinking factor, as Eberhard does, as a weight with which a unitary change
into a momentum eigenstate might occur, because the weights for the various
processes would depend not on the nature of the interaction but on the
structure of the incoming state.) We need to be sure that E.I. does not follow
equally on my account as on the hidden scattering account. But this is easy.
The weights here are each 1. Each interaction scatters entirely into a single
direction, and it is entirely responsible for all the scattering that occurs
into that direction. So ![]() and
hence
and
hence
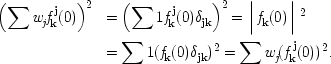
So E.I. does not plague the view that combines reductions into different momentum eigenstates to get the mixture D′, though it does plague the composition of hidden scattering processes, as Eberhard shows. But this latter view is not one I would incline to, since it is not one that allows for the preparation of momentum eigenstates in scattering interactions.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2500
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved