| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Essay 1 Causal Laws and Effective Strategies
Introduction
There are at least two kinds of laws of nature: laws of association and causal laws. Laws of association are the familiar laws with which philosophers usually deal. These laws tell how often two qualities or quantities are co-associated. They may be either deterministicthe association is universalor probabilistic. The equations of physics are a good example: whenever the force on a classical particle of mass m is f the acceleration is f/m. Laws of association may be time indexed, as in the probabilistic laws of Mendelian genetics, but, apart from the asymmetries imposed by time indexing, these laws are causally neutral. They tell how often two qualities co-occur; but they provide no account of what makes things happen.
Causal laws, by contrast, have the word causeor some causal surrogateright in them. Smoking causes lung cancer; perspiration attracts wood ticks; or, for an example from physics, force causes change in motion: to quote Einstein and Infeld, The action of an external force changes the velocity . . . such a force either increases or decreases the velocity according to whether it acts in the direction of motion or in the opposite direction.1
Bertrand Russell argued that laws of association are all the laws there are, and that causal principles cannot be derived from the causally symmetric laws of association.2 I shall here argue in support of Russell's second claim, but against the first. Causal principles cannot be reduced to laws of association; but they cannot be done away with.
The argument in support of causal laws relies on some facts about strategies. They are illustrated in a letter which
end p.21
I recently received from TIAACREF, a company that provides insurance for college teachers. The letter begins:
It simply wouldn't be true to say,
|
Nancy L. D. Cartwright . . . if you own a TIAA life insurance policy you'll live longer. |
But it is a fact, nonetheless, that persons insured by TIAA do enjoy longer lifetimes, on the average, than persons insured by commercial insurance companies that serve the general public.
I will take as a starting point for my argument facts like
those reported by the TIAA letter: it wouldn't be true that buying a
TIAA policy would be an effective strategy for lengthening one's life. TIAA
may, of course, be mistaken; it could after all be true. What is important is
that their claim is, as they suppose, the kind of claim which is either true or
false. There is a pre-utility sense of goodness of strategy; and what is and
what is not a good strategy in this pre-utility sense is an objective fact.
Consider a second example. Building the canal in
The reason for beginning with some uncontroversial examples of effective and ineffective strategies is this: I claim causal laws cannot be done away with, for they are needed to ground the distinction between effective strategies and ineffective ones. If indeed, it isn't true that buying a TIAA policy is an effective way to lengthen one's life, but stopping smoking is, the difference between the two depends on the causal laws of our universe, and on nothing weaker. This will be argued in Part 2. Part 1 endorses the first of Russell's claims, that causal laws cannot be reduced to laws of association.
1. Statistical Analyses of Causation
I will abbreviate the causal law, C causes E
by C ![]() E.
Notice that C and E are to be filled in by general terms,
E.
Notice that C and E are to be filled in by general terms,
end p.22
and not names of particulars; for example, Force causes motion or Aspirin relieves headache. The generic law C causes E is not to be understood as a universally quantified law about particulars, even about particular causal facts. It is generically true that aspirin relieves headache even though some particular aspirins fail to do so. I will try to explain what causal laws assert by giving an account of how causal laws relate on the one hand to statistical laws, and on the other to generic truths about strategies. The first task is not straightforward; although causal laws are intimately connected with statistical laws, they cannot be reduced to them.
A primary reason for believing that causal laws cannot be reduced to probabilistic laws is broadly inductive: no attempts so far have been successful. The most notable attempts recently are by the philosophers Patrick Suppes3 and Wesley Salmon4 and, in the social sciences, by a group of sociologists and econometricians working on causal models, of whom Herbert Simon and Hubert Blalock5 are good examples.
It is not just that these attempts fail, but rather why they fail that is significant. The reason is this. As Suppes urges, a cause ought to increase the frequency of its effect. But this fact may not show up in the probabilities if other causes are at work. Background correlations between the purported cause and other causal factors may conceal the increase in probability which would otherwise appear. A simple example will illustrate.
It is generally supposed that smoking causes heart disease (S
![]() H.
Thus we may expect that the probability of heart disease on smoking is greater
than otherwise. (We can write this as either Prob(H/S) > Prob(H),
or Prob(H/S) > Prob(H/┐S), for the two are
equivalent.) This expectation is mistaken. Even if it is true that smoking
causes heart disease, the expected increase in probability will not appear if
smoking is correlated with a sufficiently strong preventative, say
H.
Thus we may expect that the probability of heart disease on smoking is greater
than otherwise. (We can write this as either Prob(H/S) > Prob(H),
or Prob(H/S) > Prob(H/┐S), for the two are
equivalent.) This expectation is mistaken. Even if it is true that smoking
causes heart disease, the expected increase in probability will not appear if
smoking is correlated with a sufficiently strong preventative, say
end p.23
exercising. (Leaving aside some niceties, we can render
Exercise prevents heart disease as X ![]() ┐H.)
To see why this is so, imagine that exercising is more effective at preventing
heart disease than smoking at causing it. Then in any population where smoking
and exercising are highly enough correlated,6 it can be true
that Prob(H/S) = Prob(H), or even Prob(H/S)
< Prob(H). For the population of smokers also contains a good many
exercisers, and when the two are in combination, the exercising tends to
dominate.
┐H.)
To see why this is so, imagine that exercising is more effective at preventing
heart disease than smoking at causing it. Then in any population where smoking
and exercising are highly enough correlated,6 it can be true
that Prob(H/S) = Prob(H), or even Prob(H/S)
< Prob(H). For the population of smokers also contains a good many
exercisers, and when the two are in combination, the exercising tends to
dominate.
It is possible to get the increase in conditional probability to reappear. The decrease arises from looking at probabilities that average over both exercisers and non-exercisers. Even though in the general population it seems better to smoke than not, in the population consisting entirely of exercisers, it is worse to smoke. This is also true in the population of non-exercisers. The expected increase in probability occurs not in the general population but in both sub-populations.
This example depends on a fact about probabilities known as Simpson's paradox,7 or sometimes as the CohenNagelSimpson paradox, because it is presented as an exercise in Morris Cohen's and Ernest Nagel's text, An Introduction to Logic and Scientific Method.8 Nagel suspects that he learned about it from G. Yule's An Introduction to the Theory of Statistics (1904), which is one of the earliest textbooks written on statistics; and indeed it is discussed at length there. The fact is this: any associationProb(A/B) = Prob(A); Prob(A/B) > Prob(A); Prob(A/B) < Prob(A)between two variables which holds in a given population can be reversed in the sub-populations by finding a third variable which is correlated with both.
In the smoking-heart disease example, the third factor is a preventative factor for the effect in question. This is just one possibility. Wesley Salmon9 has proposed different examples to show that a cause need not increase the probability of its effect. His examples also turn on Simpson's
end p.24
paradox, except that in his cases the cause is correlated, not with the presence of a negative factor, but with the absence of an even more positive one.
Salmon considers two pieces of radioactive material, uranium 238 and polonium 214. We are to draw at random one material or the other, and place it in front of a Geiger counter for some time. The polonium has a short half-life, so that the probability for some designated large number of clicks is .9; for the long-lived uranium, the probability is .1. In the situation described, where one of the two pieces is drawn at random, the total probability for a large number of clicks is (.9) + (.1) = .5. So the conditional probability for the Geiger counter to click when the uranium is present is less than the unconditional probability. But when the uranium has been drawn and the Geiger counter does register a large number of clicks, it is the uranium that causes them. The uranium decreases the probability of its effect in this case. But this is only because the even more effective polonium is absent whenever the uranium is present.
All the counter examples I know to the claim that causes increase the probability of their effects work in this same way. In all cases the cause fails to increase the probability of its effects for the same reason: in the situation described the cause is correlated with some other causal factor which dominates in its effects. This suggests that the condition as stated is too simple. A cause must increase the probability of its effects; but only in situations where such correlations are absent.
The most general situations in which a particular factor is not correlated with any other causal factors are situations in which all other causal factors are held fixed, that is situations that are homogeneous with respect to all other causal factors. In the population where everyone exercises, smoking cannot be correlated with exercising. So, too, in populations where no-one is an exerciser. I hypothesize then that the correct connection between causal laws and laws of association is this:
C causes E if and only if C increases the probability of E in every situation which is otherwise causally homogeneous with respect to E.
Carnap's notion of a state description10
can be used to pick out the causally homogeneous situations. A complete set of
causal factors for E is the set of all C i such
that either C i ![]() +EorC
i
+EorC
i ![]() ┐E.
(For short C i
┐E.
(For short C i ![]() E.)
Every possible arrangement of the factors from a set which is complete except
for C picks out a population homogeneous in all causal factors but C.
Each such arrangement is given by one of the 2n state
descriptions K j =
E.)
Every possible arrangement of the factors from a set which is complete except
for C picks out a population homogeneous in all causal factors but C.
Each such arrangement is given by one of the 2n state
descriptions K j = ![]() C
i over the set (i
ranging from 1 to n) consisting of all alternative causal factors. These
are the only situations in which probabilities tell anything about causal laws.
I will refer to them as test situations for the law C
C
i over the set (i
ranging from 1 to n) consisting of all alternative causal factors. These
are the only situations in which probabilities tell anything about causal laws.
I will refer to them as test situations for the law C ![]() E.
E.
Using this notation the connection between laws of association and causal laws is this:
CC: C ![]() E
iff Prob(E/C.K j ) > Prob(E/K
j ) for all state descriptions K j
over the set where satisfies
E
iff Prob(E/C.K j ) > Prob(E/K
j ) for all state descriptions K j
over the set where satisfies
|
(i) |
C i |
|
(ii) |
C |
|
(iii) |
|
|
(iv) |
C i |
Condition (iv) is added to ensure that the state descriptions do not hold fixed any factors in the causal chain from C to E. It will be discussed further in the section after next.
Obviously CC does not provide an analysis of the
schema C ![]() E,
because exactly the same schema appears on both sides of the equivalence. But
it does impose mutual constraints, so that given sets of causal and
associational laws cannot be arbitrarily conjoined. CC is, I believe,
the strongest connection that can be drawn between causal laws and laws of
association.
E,
because exactly the same schema appears on both sides of the equivalence. But
it does impose mutual constraints, so that given sets of causal and
associational laws cannot be arbitrarily conjoined. CC is, I believe,
the strongest connection that can be drawn between causal laws and laws of
association.
1.1 Two Advantages for Scientific Explanation
C. G. Hempel's original account of inductive-statistical explanation11 had two crucial features which have been given up in later accounts, particularly in Salmon's: (1) an
end p.26
explanatory factor must increase the probability of the fact to be explained; (2) what counts as a good explanation is an objective, person-independent matter. Both of these features seem to me to be right. If we use causal laws in explanations, we can keep both these requirements and still admit as good explanations just those cases that are supposed to argue against them.
(i) Hempel insisted that an explanatory factor increase the probability of the phenomenon it explains. This is an entirely plausible requirement, although there is a kind of explanation for which it is not appropriate. In one sense, to explain a phenomenon is to locate it in a nomic pattern. The aim is to lay out all the laws relevant to the phenomenon; and it is irrelevant to this aim whether the phenomenon has high or low probability under these laws. Although this seems to be the kind of explanation that Richard Jeffrey describes in Statistical Explanation vs. Statistical Inference,12 it is not the kind of explanation that other of Hempel's critics have in mind. Salmon, for instance, is clearly concerned with causal explanation.13 Even for causal explanation Salmon thinks the explanatory factor may decrease the probability of the factor to be explained. He supports this with the uraniumplutonium example described above.
What makes the uranium count as a good explanation for the clicks in the Geiger counter, however, is not the probabilistic law Salmon cites (Prob(clicks/uranium) < Prob(clicks)), but rather the causal lawUranium causes radioactivity. As required, the probability for radioactive decay increases when the cause is present, for every test situation. There is a higher level of radioactivity when uranium is added both for situations in which polonium is present, and for situations in which polonium is absent. Salmon sees the probability
end p.27
decreasing because he attends to a population which is not causally homogeneous.
Insisting on increase in probability across all test situations not only lets in the good cases of explanation which Salmon cites; it also rules out some bad explanations that must be admitted by Salmon. For example, consider a case which, so far as the law of association is concerned, is structurally similar to Salmon's uranium example. I consider eradicating the poison oak at the bottom of my garden by spraying it with defoliant. The can of defoliant claims that the spray is 90 per cent effective; that is, the probability of a plant's dying given that it is sprayed is .9, and the probability of its surviving is .1. Here in contrast to the uranium case only the probable outcome, and not the improbable, is explained by the spraying. One can explain why some plants died by remarking that they were sprayed with a powerful defoliant; but this will not explain why some survive.14
The difference is in the causal laws. In the favourable example, it is true both that uranium causes high levels of radioactivity and that uranium causes low levels of radioactivity. This is borne out in the laws of association. Holding fixed other causal factors for a given level of decay, either high or low, it is more probable that that level will be reached if uranium is added than not. This is not so in the unfavourable case. It is true that spraying with defoliant causes death in plants, but it is not true that spraying also causes survival. Holding fixed other causes of death, spraying with my defoliant will increase the probability of a plant's dying; but holding fixed other causes of survival, spraying with that defoliant will decrease, not increase, the chances of a plant's surviving.
(ii) All these explanations are explanations by appeal to causal laws. Accounts, like Hempel's or Salmon's or Suppes's, which instead explain by appeal to laws of association, are plagued by the reference class problem. All these accounts allow that one factor explains another just in case some privileged statistical relation obtains between them. (For
end p.28
Hempel the probability of the first factor on the second must be high; for Suppes it must be higher than when the second factor is absent; Salmon merely requires that the probabilities be different.) But whether the designated statistical relation obtains or not depends on what reference class one chooses to look in, or on what description one gives to the background situation. Relative to the description that either the uranium or the polonium is drawn at random, the probability of a large number of clicks is lower when the uranium is present than it is otherwise. Relative to the description that polonium and all other radio-active substances are absent, the probability is higher.
Salmon solves this problem by choosing as the privileged description the description assumed in the request for explanation. This makes explanation a subjective matter. Whether the uranium explains the clicks depends on what information the questioner has to hand, or on what descriptions are of interest to him. But the explanation that Hempel aimed to characterize was in no way subjective. What explains what depends on the laws and facts true in our world, and cannot be adjusted by shifting our interest or our focus.
Explanation by causal law satisfies this requirement. Which causal laws are true and which are not is an objective matter. Admittedly certain statistical relations must obtain; the cause must increase the probability of its effect. But no reference class problem arises. In how much detail should we describe the situations in which this relation must obtain? We must include all and only the other causally relevant features. What interests we have, or what information we focus on, is irrelevant.
I will not here offer a model of causal explanation, but certain negative theses follow from my theory. Note particularly that falling under a causal law (plus the existence of suitable initial conditions) is neither necessary nor sufficient for explaining a phenomenon.
It is not sufficient because a single phenomenon may be in the domain of various causal laws, and in many cases it will be a legitimate question to ask, Which of these causal factors actually brought about the effect on this occasion? This problem is not peculiar to explanation by causal law,
end p.29
however. Both Hempel in his inductivestatistical model and Salmon in the statistical relevance account sidestep the issue by requiring that a full explanation cite all the possibly relevant factors, and not select among them.
Conversely, under the plausible assumption that singular causal statements are transitive, falling under a causal law is not necessary for explanation either. This results from the fact that (as CC makes plain) causal laws are not transitive. Hence a phenomenon may be explained by a factor to which it is linked by a sequence of intervening steps, each step falling under a causal law, without there being any causal law that links the explanans itself with the phenomenon to be explained.
1.2 Some Details and Some Difficulties
Before carrying on to Part 2, some details should be noted and some defects admitted.
(a) Condition (iv). Condition (iv) is added to the
above characterization to avoid referring to singular causal facts. A test
situation for C ![]() E
is meant to pick out a (hypothetical, infinite) population of individuals which
are alike in all causal factors for E, except those which on that occasion
are caused by C itself. The test situations should not hold fixed
factors in the causal chain from C to E. If it did so, the
probabilities in the populations where all the necessary intermediate steps
occur would be misleadingly high; and where they do not occur, misleadingly
low. Condition (iv) is added to except factors caused by C itself from
the description of the test situation. Unfortunately it is too strong. For
condition (iv) excepts any factor which may be caused by C even
on those particular occasions when the factor occurs for other reasons. Still,
(iv) is the best method I can think of for dealing with this problem, short of
introducing singular causal facts, and I let it stand for the nonce.
E
is meant to pick out a (hypothetical, infinite) population of individuals which
are alike in all causal factors for E, except those which on that occasion
are caused by C itself. The test situations should not hold fixed
factors in the causal chain from C to E. If it did so, the
probabilities in the populations where all the necessary intermediate steps
occur would be misleadingly high; and where they do not occur, misleadingly
low. Condition (iv) is added to except factors caused by C itself from
the description of the test situation. Unfortunately it is too strong. For
condition (iv) excepts any factor which may be caused by C even
on those particular occasions when the factor occurs for other reasons. Still,
(iv) is the best method I can think of for dealing with this problem, short of
introducing singular causal facts, and I let it stand for the nonce.
(b) Interactions. One may ask, But might it not happen
that Prob(E/C) > Prob(E) in all causally fixed
circumstances, and still C not be a cause of E? I do not know. I
am unable to imagine convincing examples in which it occurs; but that is hardly
an answer. But one kind of example is clearly taken account of. That is the
problem of spurious correlation (sometimes called the problem of joint
effects). If two factors E 1 and E 2 are
both effects of a third factor C, then it will frequently happen that
the probability of the first factor is greater when the second is present than
otherwise, over a wide variety of circumstances. Yet we do not want to assert E
1 ![]() E
2 . According to principle CC, however, E 1
E
2 . According to principle CC, however, E 1
![]() E
2 only if Prob(E 1 /E 2 ) >
Prob(E 1 ) both when C obtains, and also when C
does not obtain. But the story that E 1 and E 2
are joint effects of C provides no warrant for expecting either of these
increases.
E
2 only if Prob(E 1 /E 2 ) >
Prob(E 1 ) both when C obtains, and also when C
does not obtain. But the story that E 1 and E 2
are joint effects of C provides no warrant for expecting either of these
increases.
One may have a worry in the other direction as well. Must a cause increase the probability of its effect in every causally fixed situation? Might it not do so in some, but not in all? I think not. Whenever a cause fails to increase the probability of its effect, there must be a reason. Two kinds of reasons seem possible. The first is that the cause may be correlated with other causal factors. This kind of reason is taken account of. The second is that interaction may occur. Two causal factors are interactive if in combination they act like a single causal factor whose effects are different from at least one of the two acting separately. For example, ingesting an acid poison may cause death; so too may the ingestion of an alkali poison. But ingesting both may have no effect at all on survival.
In this case, it seems, there are three causal truths: (1) ingesting acid without ingesting alkali causes death; (2) ingesting alkali without ingesting acid causes death; and (3) ingesting both alkali and acid does not cause death. All three of these general truths should accord with CC.
Treating interactions in this way may seem to trivialize the analysis; anything may count as a cause. Take any factor that behaves sporadically across variation of causal circumstances. May we not count it as a cause by looking at it separately in those situations where the probability increases, and claim it to be in interaction in any case where the probability does not increase? No. There is no guarantee that this can always be done. For interaction is always interaction with some other causal factor; and it is not always possible to find some other factor, or conjunction of factors,
end p.31
which obtain just when the probability of E on the factor at issue decreases, and which itself satisfies principle CC relative to all other causal factors.15 Obviously, considerably more has to be said about interactions; but this fact at least makes it reasonable to hope they can be dealt with adequately, and that the requirement of increase in probability across all causal situations is not too strong.
(c) 0, 1 probabilities and threshold effects.
Principle CC as it stands does not allow C ![]() E
if there is even a single arrangement of other factors for which the
probability of E is one, independent of whether C occurs or not.
So CC should be amended to read:
E
if there is even a single arrangement of other factors for which the
probability of E is one, independent of whether C occurs or not.
So CC should be amended to read:
It is a consequence of the second conjunct that something that occurs universally can be the consequent of no causal laws. The alternative is to let anything count as the cause of a universal fact.
There is also no natural way to deal with threshold effects, if there are any. If the probability of some phenomenon can be raised just so high, and no higher, the treatment as it stands allows no genuine causes for it.
(d) Time and causation. CC makes no mention of time. The properties may be time indexed; taking aspirins at t causes relief at t + Δt, but the ordering of the indices plays no part in the condition. Time ordering is often introduced in statistical analyses of causation to guarantee the requisite asymmetries. Some, for example, take increase in conditional probability as their basis. But the causal arrow is asymmetric, whereas increase in conditional probability is symmetric: Prob(E/C) > Prob(E) iff Prob(C/E) > Prob(C). This problem does not arise for CC, because the set of alternative causal factors for E will be different from the set of alternative causal factors for C. I take it to be an advantage that my account leaves open the question of backwards causation. I doubt that we shall ever find compelling examples of it; but if there
end p.32
were a case in which a later factor increased the probability of an earlier one in all test situations, it might well be best to count it a cause.
2. Probabilities in Decision Theory
Standard versions of decision theory require two kinds of information. (1) How desirable are various combinations of goals and strategies and (2) how effective are various strategies for obtaining particular goals. The first is a question of utilities, which I will not discuss. The second is a matter of effectiveness; it is generally rendered as a question about probabilities. We need to know what may roughly be characterized as the probability that the goal will result if the strategy is followed. It is customary to measure effectiveness by the conditional probability. Following this custom, we could define
!S is an effective strategy for G iff Prob(G/S) > Prob(G).
I have here used the volative mood marker ! introduced by H. P. Grice,16 to be read let it be the case that. I shall refer to S as the strategy state. For example, if we want to know whether the defoliant is effective for killing poison oak, the relevant strategy state is a poison oak plant is sprayed with defoliant. On the above characterization, the defoliant is effective just in case the probability of a plant's dying, given that it has been sprayed, is greater than the probability of its dying given that it has not been sprayed. Under this characterization the distinction between effective and ineffective strategies depends entirely on what laws of association obtain.
But the conditional probability will not serve in this way, a fact that has been urged by Allan Gibbard and William Harper.17 Harper and Gibbard point out that the increase in conditional probability may be spurious, and
end p.33
that spurious correlations are no grounds for action. Their own examples are somewhat complex because they specifically address a doctrine of Richard Jeffrey's not immediately to the point here. We can illustrate with the TIAA case already introduced. The probability of long life given that one has a TIAA policy is higher than otherwise. But, as the letter says, it would be a poor strategy to buy TIAA in order to increase one's life expectancy.
The problem of spurious correlation in decision theory leads naturally to the introduction of counterfactuals. We are not, the argument goes, interested in how many people have long lives among people insured by TIAA, but rather in the probability that one would have a long life if one were insured with TIAA. Apt as this suggestion is, it requires us to evaluate the probability of counterfactuals, for which we have only the beginnings of a semantics (via the device of measures over possible worlds)18 and no methodology, much less an account of why the methodology is suited to the semantics. How do we test claims about probabilities of counterfactuals? We have no answer, much less an answer that fits with our nascent semantics. It would be preferable to have a measure of effectiveness that requires only probabilities over events that can be tested in the actual world in the standard ways. This is what I shall propose.
The Gibbard and Harper example, an example of spurious correlation due to a joint cause, is a special case of a general problem. We saw that the conditional probability will not serve as a mark of causation in situations where the putative cause is correlated with other causal factors. Exactly the same problem arises for effectiveness. For whatever reason the correlation obtains, the conditional probability is not a good measure of effectiveness in any populations where the strategy state is correlated with other factors causally relevant to the goal state. Increase in conditional probability is no mark of effectiveness in situations which are causally heterogeneous. It is necessary, therefore, to make the same
end p.34
restrictions about test situations in dealing with strategies that we made in dealing with causes:
!S is an effective strategy for obtaining G in situation L iff Prob(G/S.K L ) > Prob(G/K L ).
Here K L is the state description true in L, taken over the complete set of causal factors for G, barring S. But L may not fix a unique state description. For example L may be the situation I am in when I decide whether to smoke or not, and at the time of the decision it is not determined whether I will be an exerciser. In that case we should compare not the actual values Prob(G/S.K L ) and Prob(G/K L ), but rather their expected values:
SC: !S is an effective strategy for obtaining G in L iff
where j ranges over all K j consistent with L.19
This formula for computing the effectiveness of strategies has several desired features: (1) it is a function of the probability measure, Prob, given by the laws of association in the actual world; and hence calculable by standard methods of statistical inference. (2) It reduces to the conditional probability in cases where it ought. (3) It restores a natural connection between causes and strategies.
(1) SC avoids probabilities over counterfactuals. Implications of the arguments presented here for constructing a semantics for probabilities for counterfactuals will be pointed out in section 2.2.
(2) Troubles for the conditional probability arise in cases like the TIAA example in which there is a correlation between the proposed strategy and (other) causal factors for the goal in question. When such correlations are absent, the conditional probability should serve. This follows immediately: when there are no correlations between S and other causal factors, Prob(K j /S) = Prob(K j ); so the left-hand side of SC reduces to Prob(G/S) in the situation L and the right-hand side to Prob(G) in L.
(3) There is a natural connection between causes and
strategies that should be maintained; if one wants to obtain a goal, it is a
good (in the pre-utility sense of good) strategy to introduce a cause for that
goal. So long as one holds both the simple view that increase in conditional
probability is a sure mark of causation and the view that conditional
probabilities are the right measure of effectiveness, the connection is
straightforward. The arguments in Part 1 against the simple view of causation
break this connection. But SC re-establishes it, for it is easy to see
from the combination of CC and SC that if X ![]() G
is true, then !X will be an effective strategy for G in any
situation.
G
is true, then !X will be an effective strategy for G in any
situation.
2.1. Causal Laws and Effective Strategies
Although SC joins causes and strategies, it is not this connection that argues for the objectivity of sui generis causal laws. As we have just seen, one could maintain the connection between causes and strategies, and still hope to eliminate causal laws by using simple conditional probability to treat both ideas. The reason causal laws are needed in characterizing effectiveness is that they pick out the right properties on which to condition. The K j which are required to characterize effective strategies must range over all and only the causal factors for G.
It is easy to see, from the examples of Part 1, why the K j must include all the causal factors. If any are left out, cases like the smoking-heart disease example may arise. If exercising is not among the factors which K j fixes, the conditional probability of heart disease on smoking may be less than otherwise in K j , and smoking will wrongly appear as an effective strategy for preventing heart disease.
It is equally important that the K j not include too much. partitions the space of possible situations. To partition too finely is as bad as not to partition finely enough. Partitioning on an irrelevancy can make a genuine cause look irrelevant, or make an irrelevant factor look like a cause. Earlier discussion of Simpson's paradox shows that this is
end p.36
structurally possible. Any association between two factors C and E can be reversed by finding a third factor which is correlated in the right way with both. When the third factor is a causal factor, the smaller classes are the right ones to use for judging causal relations between C and E. In these, whatever effects the third factor has on E are held fixed in comparing the effects of C versus those of ┐C. But when the third factor is causally irrelevant to Ethat is, when it has no effects on Ethere is no reason for it to be held fixed, and holding it fixed gives wrong judgements both about causes and about strategies.
I will illustrate from a real life case.20
The graduate school at
This analysis seems to exonerate
end p.37
applicants were partitioned according to their roller skating ability that would count as no defence.22 Why is this so?
The difference between the two situations lies in our
antecedent causal knowledge. We know that applying to a popular department (one
with considerably more applicants than positions) is just the kind of thing
that causes rejection. But without a good deal more detail, we are not prepared
to accept the principle that being a good roller skater causes a person to be
rejected by the
The
2.2. Alternative Accounts Which Employ True Probabilities Or Counterfactuals
One may object: once all causally relevant factors have been fixed, there is no harm in finer partitioning by causally irrelevant factors. Contrary to what is claimed in the remarks about roller skating and admission rates, further partitioning will not change the probabilities. There is a difference between true probabilities and observed relative frequencies. Admittedly it is likely that one can always find some third, irrelevant, variable which, on the basis of estimates from finite data, appears to be correlated with both the cause and effect in just the ways required for Simpson's paradox. But we are concerned here not with finite frequencies, or estimates from them, but rather with true probabilities. You misread the true probabilities from the finite data, and think that correlations exist where they do not.
end p.38
For this objection to succeed, an explication is required of the idea of a true probability, and this explication must make plausible the claim that partitions by what are pre-analytically regarded as non-causal factors do not result in different probabilities. It is not enough to urge the general point that the best estimate often differs from the true probability; there must in addition be reason to think that that is happening in every case where too-fine partitioning seems to generate implausible causal hypotheses. This is not an easy task, for often the correlations one would want to classify as false are empirically indistinguishable from others that ought to be classified true. The misleading, or false, correlations sometimes pass statistical tests of any degree of stringency we are willing to accept as a general requirement for inferring probabilities from finite data. They will often, for example, be stable both across time and across randomly selected samples.
To insist that these stable frequencies are not true probabilities is to give away too much of the empiricist programme. In the original this programme made two assumptions. First, claims about probabilities are grounded only in stable frequencies. There are notorious problems about finite versus infinite ensembles, but at least this much is certain: what probabilities obtain depends in no way, either epistemologically or metaphysically, on what causal assumptions are made. Secondly, causal claims can be reduced completely to probabilistic claims, although further empirical facts may be required to ensure the requisite asymmetries.
I attack only the second of these two assumptions. Prior causal knowledge is needed along with probabilities to infer new causal laws. But I see no reason here to give up the first, and I think it would be a mistake to do so. Probabilities serve many other concerns than causal reasoning and it is best to keep the two as separate as possible. In his Grammar of Science Karl Pearson taught that probabilities should be theory free, and I agree. If one wishes nevertheless to mix causation and probability from the start then at least the arguments I have been giving here show some of the constraints that these true probabilities must meet.
Similar remarks apply to counterfactual analyses. One
end p.39
popular kind of counterfactual analysis would have it that
|
!S is effective strategy for G in L iff Prob(S □→ G/L) > Prob(┐ S □→ G/L)23 |
The counterfactual and the causal law approach will agree, only if
|
A: Prob(α □→ G/X) = Prob(G/α.K x ) |
where K x is the maximal causal description (barring α) consistent with X. Assuming the arguments here are right, condition A provides an adequacy criterion for any satisfactory semantics of counterfactuals and probabilities.
How Some Worlds Could not Be Hume Worlds24
The critic of causal laws will ask, what difference do they make? A succinct way of putting this question is to consider for every world its corresponding Hume worlda world just like the first in its laws of association, its temporal relations, and even in the sequences of events that occur in it. How does the world that has causal laws as well differ from the corresponding Hume world? I have already argued that the two worlds would differ with respect to strategies.
Here I want to urge a more minor point, but one that might go unnoticed: not all worlds could be turned into Hume worlds by stripping away their causal laws. Given the earlier condition relating causal laws and laws of association, many worlds do not have related Hume worlds. In fact no world whose laws of association provide any correlations could be turned into a Hume world. The demonstration is trivial. Assume that a given world has no causal laws for a particular kind of phenomenon E. The earlier condition tells us to test for causes of E by looking for factors that increase the probability of E in maximal causally homogeneous sub-populations. But in the Hume world there are no causes, so every sub-population is homogeneous in all causal factors, and the maximal homogeneous population is the whole population. So if there is any C such that Prob(E/C) > Prob(E), it will be true that C causes E, and this world will not be a Hume world after all.
Apparently the laws of association underdetermine the causal
laws. It is easy to construct examples in which there are two properties, P
and Q, which could be used to partition a population. Under the
partition into P and ┐ P, C increases the
conditional probability of E in both sub-populations; but under the
partition into Q and ┐ Q, Prob(E/C) = Prob(E).
So relative to the assumption that P causes E, but Q does
not, C causes E is true. It is false relative to the assumption
that Q ![]() E,
and P
E,
and P ![]() E.
This suggests that, for a given set of laws of association, any set of causal
laws will do. Once some causal laws have been settled, others will
automatically follow, but any starting point is as good as any other. This
suggestion is mistaken. Sometimes the causal laws are underdetermined by the
laws of association, but not always. Some laws of association are compatible
with only one set of causal laws. In general laws of association do not entail
causal laws: but in particular cases they can. Here is an example.
E.
This suggests that, for a given set of laws of association, any set of causal
laws will do. Once some causal laws have been settled, others will
automatically follow, but any starting point is as good as any other. This
suggestion is mistaken. Sometimes the causal laws are underdetermined by the
laws of association, but not always. Some laws of association are compatible
with only one set of causal laws. In general laws of association do not entail
causal laws: but in particular cases they can. Here is an example.
Consider a world whose laws of association cover three properties, A, B, and C; and assume that the following are implied by the laws of association:
|
(1) |
Prob(C/A) > Prob(C) |
|
(2) |
Prob(C/B & A > Prob(C/A); Prob(C/B & ┐ A) > Prob(C/┐A) |
|
(3) |
Prob(C/B) = Prob(C) |
In this world, B ![]() C.
The probabilities might for instance be those given in Chart 1. From just the
probabilistic facts (1), (2), and (3), it is possible to infer that both A
and B are causally relevant to C. Assume B
C.
The probabilities might for instance be those given in Chart 1. From just the
probabilistic facts (1), (2), and (3), it is possible to infer that both A
and B are causally relevant to C. Assume B ![]() C.
Then by (1), A
C.
Then by (1), A ![]() C,
since the entire population is causally homogeneous (barring A) with
respect to C and hence counts as a test population for A's
effects on C. But if
C,
since the entire population is causally homogeneous (barring A) with
respect to C and hence counts as a test population for A's
effects on C. But if
end p.41
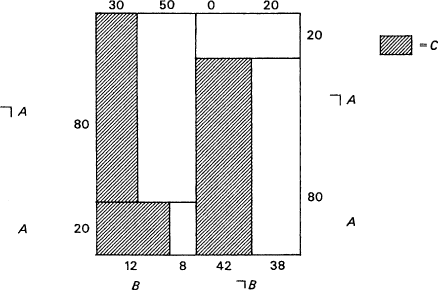
Chart 1
A ![]() C,
then by (2), B
C,
then by (2), B ![]() C.
Therefore B
C.
Therefore B ![]() C.
But from (3) this is not possible unless A is also relevant, either positively
or negatively, to C. In the particular example pictured in the chart, A
and B are both positively relevant to C.
C.
But from (3) this is not possible unless A is also relevant, either positively
or negatively, to C. In the particular example pictured in the chart, A
and B are both positively relevant to C.
This kind of example may provide solace to the Humean. Often Humeans reject causal laws because they have no independent access to them. They suppose themselves able to determine the laws of association, but they imagine that they never have the initial causal information to begin to apply condition C. If they are lucky, this initial knowledge may not be necessary. Perhaps they live in a world that is not a Hume world; it may nevertheless be a world where causal laws can be inferred just from laws of association.
4. Conclusion
The quantity Prob(E/C.K j ), which appears in both the causal condition of Part 1 and in the measure of effectiveness from Part 2, is called by statisticians the partial conditional probability of E on C, holding K j fixed; and it is used in ways similar to the ways I have used it here. It forms the foundation
end p.42
for regression analyses of causation and it is applied by both Suppes and Salmon to treat the problem of joint effects. In decision theory the formula SC is structurally identical to one proposed by Brian Skyrms in his deft solution to New-comb's paradox; and elaborated further in his book Causal Necessity.25 What is especially significant about the partial conditional probabilities which appear here is the fact that these hold fixed all and only causal factors.
The choice of partition, , is the critical feature of the measure of effectiveness proposed in SC. This is both (a) what makes the formula work in cases where the simple conditional probability fails; and (b) what makes it necessary to admit causal laws if you wish to sort good strategies from bad. The way you partition is crucial. In general you get different results from SC if you partition in different ways. Consider two different partitions for the same space, K 1 , . . . , K n and I 1 , . . . I s , which cross-grain each otherthe K i are mutually disjoint and exhaustive, and so are the I j . Then it is easy to produce a measure over the field (G, C, K i , I j ) such that
What partition is employed is thus essential to whether a strategy appears effective or not. The right partitionthe one that judges strategies to be effective or ineffective in accord with what is objectively trueis determined by what the causal laws are. Partitions by other factors will give other results; and, if you do not admit causal laws, there is no general procedure for picking out the right factors. The objectivity of strategies requires the objectivity of causal laws.
end p.43
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2833
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved