| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The Simulacrum Account of Explanation
Introduction
We saw in the last chapter that the bridge principles in a theory like quantum mechanics are few in number, and they deal primarily with highly fictionalized descriptions. Why should this be so? Some work of T. S. Kuhn suggests an answer. In his paper, A Function for Measurement in the Physical Sciences, and in other papers with the word function in the title, Kuhn tries something like functional explanations of scientific practice. Anthropologists find a people with a peculiar custom. The people themselves give several or maybe no reasons for their custom. But the anthropologist conjectures that the custom remains among these people not only for their avowed reasons, but also because other customs or ecological conditions make it very difficult for their society to survive without it. This then is the function of the custom in question, even though it is not practised with any conscious awareness of that function. Naturally all functional explanations have a dubious logic, but they do often bring out instructive aspects of the custom in question.
Now let us ask what function might be served by having relatively few bridge principles to hand when we are engaged in constructing models of phenomena. Kuhn concludes his paper on measurement by saying he believes that the nineteenth century mathematization of physical science produced vastly refined professional criteria for problem selection and that it simultaneously very much increased the effectiveness of professional verification procedures.1 I think that something similar is to be said about having a rather small number of bridge principles. The phenomena to be described are endlessly complex. In order to pursue any collective research, a group must be able to delimit the kinds of models that are even contenders. If there were endlessly many possible ways for a particular research community to hook up phenomena with intellectual constructions, model building would be entirely chaotic, and there would be no consensus of shared problems on which to work.
The limitation on bridge principles provides a consensus within which to formulate theoretical explanations and allows for relatively few free parameters in the construction of models. This in turn provides sharp criteria for problem selection. Naturally there may be substantial change in the structure of bridge principles if nothing works; but we hang on to them while we can. It is precisely the existence of relatively few bridge principles that makes possible the construction, evaluation, and elimination of models. This fact appears also to have highly anti-realist side effects. As we have seen, it strongly increases the likelihood that there will be literally incompatible models that all fit the facts so far as the bridge principles can discriminate.
This is just a sketch of a Kuhnian account, but one which I believe is worth pursuing. Borrowing a term from the historians of science, it might be called an external account of why bridge principles need to be limited in number. But it fits nicely with a parallel internal account, one that holds that the limitation on bridge principles is crucial to the explanatory power of the theory. I will argue for this internal account in section 1 of this essay. In section 2 I propose a model of explanation that allows for the paucity of bridge principles and makes plain the role of fictionalized descriptions.
1. Bridge Principles and Realistic Models
A good theory aims to cover a wide variety of phenomena with as few principles as possible. That includes bridge principles. It is a poor theory that requires a new Hamiltonian for each new physical circumstance. The great explanatory power of quantum mechanics comes from its ability to deploy a small number of well-understood Hamiltonians to cover a broad range of cases, and not from its ability to match each situation one-to-one with a new mathematical representation. That way of proceeding would be crazy.
This is an obvious fact about what theories must be like if they are to be manageable at all. But it has the anti-realist consequences that we have seen. Why have realists not been more troubled by this fact? The answer, I think, is that many realists suppose that nature conspires to limit the number of bridge principles. Only a few bridge principles are needed because only a small number of basic interactions exist in nature. An ideal theory will represent each of the basic interactions; new cases will not require new bridge principles because the representation for complex situations can be constructed from the representations for the basic components.
I think that this is a radically mistaken point of view. First, it is a model of a physics we do not have. That is a familiar point by now. Much worse, it is a model of a physics we do not want. The piecing-together procedure would be unbearably complex. It goes in exactly the wrong direction. The beauty and strength of contemporary physics lies in its ability to give simple treatments with simple models, where at least the behaviour in the model can be understood and the equations can not only be written down but can even be solved in approximation. The harmonic oscillator model is a case in point. It is used repeatedly in quantum mechanics, even when it is difficult to figure out exactly what is supposed to be oscillating: the hydrogen atom is pictured as an oscillating electron; the electromagnetic field as a collection of quantized oscillators; the laser as a van der Pol oscillator; and so forth. The same description deployed again and again gives explanatory power.
It is best to illustrate with a concrete case. In the last essay we looked to elementary texts for examples of bridge principles. Here I will present a more sophisticated example: a quantum theoretical account of a laser. Recall from Essay that there are a variety of methods for treating lasers in quantum mechanics. One is the quantum statistical approach in which a master equation (or a Langevin equation) is derived for the system. This kind of approach is familiar from our discussion in Essay 6 of the Markov approximation for radiating atoms, so this is a good example to choose.
There is a thorough development of this method in William Louisell's Quantum Statistical Properties of Radiation.2 The treatment there is most suitable for a gas laser, such as the early helium-neon laser. Louisell proposes what he calls a block diagram. (See Figure 8.1.) He imagines that the laser consists of three-level atoms in interaction with a quantized electromagnetic field. Before the quantum statistical approach, treatments of lasers were generally semi-classical: the atoms were quantized but the field was not. Louisell also explicitly includes the interaction of both the atoms and the field with a damping reservoir. These two features are important for they allow the derivation of correlations among the emitted photons which are difficult to duplicate in the earlier semi-classical approaches.
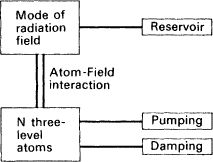
Fig. 8.1. Block diagram of laser model. (Source: Louisell, Quantum Statistical Properties of Radiation.)
In Essay 6 I talked briefly about idealizations that are hard to eliminate at the theoretical level. Here is a good illustration. Louisell supposes that the atoms are uniformly distributed, N per unit volume, and that they do not interact with each other: They are coupled to each other only through their atom-field interaction.3 In reality the atoms do interact, though this does not have much effect on the performance of the laser. The missing effects can sometimes be corrected for, but this is done piece-meal when the theory is applied and not by adding terms to the fundamental Hamiltonian given in the theoretical treatment.
Louisell's equation for the system represented by his block diagram consists of three parts. I will write it here just for reference:
He tells us of this equation that the first terms describe the causal behavior. The second term describes the interaction of the field mode with its reservoir . . . The last term describes the interaction of the atoms with their pumping and damping reservoirs.4 This equation is deceptively simple because it is still just a schema. We do not yet know how W, (∂S/∂t) F , and so forth are to be represented for the block laser. This is where bridge principles enter. A page and a half later when these variables have been filled in, this simple-seeming equation will take twelve lines of text for Louisell to write.
The first term is supposed to represent the causal behaviour, in contrast with the last two terms. Another common way of expressing this contrast would be to say: the atom-field interaction is represented realistically, but the terms for the reservoir interactions are just phenomenological. Louisell's method of expression is better because it is narrower. Physicists use realistic in a variety of senses. One common sense contrasts realistic with idealized. This sense concerns the relation between the model and the situation depicted in the model: how well do the prepared and the unprepared descriptions match? We have seen that Louisell's treatment of the atoms is highly idealized. So too are other aspects of his block diagram. In this sense, Louisell's model for the causal behaviour is not very realistic.
There is another, different way in which physicists use the word realistic. I will illustrate with three examples. The first example comes from the laser engineering course I referred to in the last essay.5 After several lectures on classical electron oscillators, Professor Anthony Siegman announced that he was ready to talk about the lasing medium in a real laser. I thought he was going to teach about ruby rodsthat ruby is chromium doped sapphire, that the 3+ chromium ions are interspersed randomly at low densities throughout the sapphire lattice, and that an ordinary electric discharge is used to excite the chromium ions and bring about a population inversion. Instead he began, Consider a collection of two-level atoms. In a sense he started to talk about real lasersa laser medium is indeed composed of quantized systems like atoms, and not of the fictitious electron oscillators. But in another sense he did not: two-level atoms are but a crude stand-in for the intricate and variegated structure of real laser materials.
The second example comes from a conversation with my
colleague Francis Everitt, an experimental physicist whom I have mentioned
before in connection with his historical work on James Clerk Maxwell. In the
last essay we saw that a laser can be treated by van der Pol's equation: in a
variety of ways the laser will behave like a triode oscillator in a
The third example gives an explicit clue. In the text Quantum Optics John Klauder and E. C. G. Sudarshan report, A number of authors have treated idealized interacting systems as models for lasers.6 Louisell is an example. Although highly idealized, the Louisell model is still realistic in a way in which the models of Klauder and Sudarshan are not. They themselves describe their models as phenomenological. What do they mean? They say that their models are phenomenological because the models work directly on the state . . . as a function of time and do not derive it as a solution to a Hamiltonian.7 Recall that the Hamiltonian goes into the Schroedinger equation and determines the time evolution of the state. It represents the energies which guide the behaviour of the system. Sudarshan and Klauder aim to get the right state; but they write down this state directly, post hoc, with an eye to the behaviour it is supposed to predict. They do not write down a Schroedinger equation and derive the state as a solution to it; and thus they do not show what energies produce the state. Their treatment is unrealistic from the point of view of the explanatory theory. It gives a theoretical description of the behaviour, but nothing in the model shows what gives rise to this behaviour.
Look back now to the damping reservoir, and recall our discussion of atomic radiation in Essay 6. The effect of a damping reservoir is to bring about an irreversible change in the system which couples to it. Information which goes into the reservoir gets lost there, and the memory of the system is erased. The reservoir is a way of representing the walls of the cavity and of the surrounding environment. But it is like the proverbial black box. It generates the effects that the walls are supposed to have, but there is no representation of the method by which the walls produce these effects. No description is given of how the walls are made up, or of what gives rise to the formal characteristics that reservoirs must have to bring about damping. This contrasts with Siegman's treatment of the lasing medium. Two-level atoms are not very much like chromium ions in a ruby laser. But they do give rise to equations in accord with established explanatory principles and not in an ad hoc way.
The two senses of realistic act at different levels. The first bears on the relation between the model and the world. The model is realistic if it presents an accurate picture of the situation modelled: it describes the real constituents of the systemthe substances and fields that make it upand ascribes to them characteristics and relations that actually obtain. The second sense bears on the relation between the
149
model and the mathematics. A fundamental theory must supply a criterion for what is to count as explanatory. Relative to that criterion the model is realistic if it explains the mathematical representation.
The two senses of realistic are nicely illustrated in Louisell's treatment. We have already seen that Louisell's model is only quasi-realistic in the first sense. It describes the significant components, but the features it ascribes to them are a caricature of those in reality. The model is both realistic and unrealistic in the second sense as well. The first term in Louisell's equation represents the potential arising from the atom-field interaction which he sets down in the model. That is what he means by saying that it represents the causal behaviour. The reservoir terms are different. They give rise to the right solutions but no concrete mechanisms are supplied in the model to explain them.
The two ways in which a model may be unrealistic are related. Louisell's modelling of the reservoir is unrealistic in the first sense as well as in the second, in part because he does not intend to use the detailed structure of the reservoir to generate his equation. But that is not all there is to it. We say in Essay 6 that if the reservoir is really to do its job in getting the atoms to decay, the time correlations there must be exactly zero. This is an assumption that Louisell makes; but it is highly unrealistic in the first sense. This case is just like the infinite potentials in the last section of the last essay. The conventional Schroedinger theory cannot be fitted exactly to the situation, so we deal with the problem by distorting the situation. But we put the distortion as far away from the system of immediate concern as possible. If we are interested in the atoms only, we can put the distortion in the description of the field, assigning it an infinite number of degrees of freedom. But if we want to study the field as well, the infinite degrees of freedom or the zero time correlations are put into the walls of the cavity and the surrounding environment. And so on.
We learn an important lesson about bridge principles from these considerations. A treatment that is more realistic in the second sense will employ more bridge principles. The quantum statistical approach is a highly sophisticated method for predicting fine details about photon statistics in laser light. Even in an advanced treatment like this, a large part of the work is done by phenomenological terms which minimize the number of bridge principles needed. For example, the phenomenological terms that Louisell employs are from his general theory of damped systems and can be employed again and again independent of how the damping is brought about.
The first term of Louisell's equation also illustrates this point about bridge principles. In the last essay I raised the worry that the bridge principles I discussed there were too elementary to be instructive. Louisell's equation shows that this is not so. Only the first term is a genuine Hamiltonian term matched by a conventional bridge principle with a description of the potential. What Hamiltonian is it? It is just the Hamiltonian for the interaction of an atom with a radiation field, which appeared on our list in Essay 7 and which was developed in a classic paper by Enrico Fermi in 1932. The only change that Louisell makes is to sum the Hamiltonian over all the atoms in the cavity. This bears out my general claim about bridge principles. The success of the quantum statistical treatment does not depend on using novel principles that are highly involved, but rather in using some well-known and well-understood principles in a novel way.
The Simulacrum Account of Explanation
The conventional D-N account supposes that we have explained a phenomenon when we have shown how it follows from a more fundamental law. This requires that the treatments we give for phenomena in physics must certainly be realistic in the first sense, and preferably in the second as well, if they are to serve as explanations. I propose an alternative to the D-N model that brings the philosophic account closer to explanatory practices in physics as I have pictured them. It is based on Duhem's view of explanation, which I sketched in Essay 5, and follows immediately from the discussion of the last section.
151
The primary aim of this book is to argue against the facticity of fundamental laws. As we saw in the very first essay, one of the chief arguments that realists use in favour of their facticity is their broad explanatory and predictive success. I have been arguing here that the vast majority of successful treatments in physics are not realistic. They are not realistic in the first sense of picturing the phenomena in an accurate way; and even in the second sense, too much realism may be a stop to explanatory power, since the use of phenomenological terms rather than a more detailed causal construction may allow us more readily to deploy known solutions with understood characteristics and thereby to extend the scope of our theory.
If what I say is correct, it calls for a new account of explanation. Recall the discussion of Essay 6. To explain a phenomenon is to find a model that fits it into the basic framework of the theory and that thus allows us to derive analogues for the messy and complicated phenomenological laws which are true of it. The models serve a variety of purposes, and individual models are to be judged according to how well they serve the purpose at hand. In each case we aim to see the phenomenon through the mathematical framework of the theory, but for different problems there are different emphases. We may wish to calculate a particular quantity with great accuracy, or to establish its precise functional relationship to another. We may wish instead to replicate a broader range of behaviour, but with less accuracy. One important thing we sometimes want to do is to lay out the causal processes which bring the phenomena about, and for this purpose it is best to use a model that treats the causally relevant factors as realistically as possible, in both senses of realistic. But this may well preclude treating other factors realistically. We should not be misled into thinking that the most realistic model will serve all purposes best.
In order to stress this anti-realistic aspect of models, I call my view of explanation a simulacrum account. The second definition of simulacrum in the Oxford English Dictionary says that a simulacrum is something having merely the form or appearance of a certain thing, without
152
without possessing its substance or
proper qualities.8 This is just what I have been urging that
models in physics are like. Is a helium-neon laser really a van der Pol
oscillator? Well, it is really a mix of helium and neon atoms, in about the
ratio nine to one, enclosed in a cavity with smooth walls and reflecting
mirrors at both ends, and hooked up to a device to pump the neon atoms into
their excited state. It is not literally a triode oscillator in a
A model is a work of fiction. Some properties ascribed to objects in the model will be genuine properties of the objects modelled, but others will be merely properties of convenience. The term properties of convenience was suggested by H. P. Grice, and it is apt. Some of the properties and relations in a model will be real properties, in the sense that other objects in other situations might genuinely have them. But they are introduced into this model as a convenience, to bring the objects modelled into the range of the mathematical theory.
Not all properties of convenience will be real ones. There are the obvious idealizations of physicsinfinite potentials, zero time correlations, perfectly rigid rods, and frictionless planes. But it would be a mistake to think entirely in terms of idealizationsof properties which we conceive as limiting cases, to which we can approach closer and closer in reality. For some properties are not even approached in reality. They are pure fictions.
I would want to argue that the probability distributions of classical statistical mechanics are an example. This is a very serious claim, and I only sketch my view here as an illustration. The distributions are essential to the theorythey are what the equations of the theory governand the theory itself is extremely powerful, for example in the detailed treatment of fluid flow. Moreover, in some simple special cases the idea of the probability distribution can be
153
operationalized; and the tests support the distributions ascribed by the theory.9
Nevertheless, I do not think these distributions are real. Statistical mechanics works in a massive number of highly differentiated and highly complex situations. In the vast majority of these it is incredible to think that there is a true probability distribution for that situation; and proofs that, for certain purposes, one distribution is as good as another, do not go any way to making it plausible that there is one at all. It is better, I think, to see these distributions as fictions, fictions that have a powerful organizing role in any case and that will not mislead us too much even should we take them to be real in the simple cases.
We can illustrate with Maxwell's treatment of the radio-meter, described in the introduction to this book. Maxwell begins with Boltzmann's equation (equation 1, Introduction), which governs the evolution of the velocity distribution of the gas molecules. (This distribution gives the probability, for every possible combination of values for v, w, x . . , that the first molecule has velocity v; the second, velocity w; the third velocity x; etc.) Maxwell writes down one of the many functions which solve Boltzmann's equation and he claims that this function is the distribution for a medium in which there are inequalities of temperature and velocity and in which the viscosity varies as the first power of the absolute temperature.10
I claim that the medium which Maxwell describes is only a model. It is not the medium which exists in any of the radiometers we find in the toy department of Woolworth's. The radiometers on the shelves in Woolworth's do not have delicate well-tuned features. They cost $2.29. They have a host of causally relevant characteristics besides the two critical ones Maxwell mentions, and they differ in these characteristics from one to another. Some have sizeable convection currents; in others the currents are negligible; probably the co-efficients of friction between vanes and
154
gases differ; as do the conduction rates, the densities of the enclosed gases, and the make-up of the gas itself.
We may be inclined to think that this does not matter much. Maxwell has made a harmless idealization: the effects of the other factors are small, and the true distribution in each Woolworth radiometer is close enough for the purposes at hand to the one Maxwell proposes. A simulacrum account is unnecessary, the standard covering-law story will do. But this is not so. For on the covering-law theory, if Maxwell's treatment is to explain the rotation in a Woolworth radiometer, the radiometer must have a specific distribution function and that function must be nomologically linked to the conditions that obtain. But Maxwell's theory records no such laws. The conditions in these radiometers are indefinitely varied and indefinitely complex, so that a multitude of highly complicated unknown laws must be assumed to save Maxwell's explanation. I think these laws are a complete fiction. We cannot write them down. We certainly cannot construct experiments to test them. Only the covering-law model of explanation argues for their existence.
Recall Hempel's worries about bridge principles, which I discussed in the last essay. Hempel was concerned that bridge principles do not have the proper exceptionless character to ensure deductive connections between explanans and explanandum. Hempel illustrated with magnets and iron filings. But Maxwell's radiometer is as good an example. Not all radiometers that meet Maxwell's two descriptions have the distribution function Maxwell writes down; most have many other relevant features besides. This will probably continue to be true no matter how many further corrections we add. In general, as Hempel concluded, the bridge law between the medium of a radiometer and a proposed distribution can hold only ceteris paribus.
This, however, is a difficult position for a covering-law theorist to take. As I argued early on, in the second essay, a law that holds only in restricted circumstances can explain only in those circumstances. The bulk of the radiometers in Woolworth's are untouched by Maxwell's explanation. The idealization story with which we began supposes that each Woolworth radiometer has some distribution function true of it and that the distribution functions in question are sufficiently close to Maxwell's. In this case Maxwell's explanation for the ideal medium serves as a proxy to the proper explanations for each of the real radiometers. But these last are no explanations at all on the covering-law view unless the Book of Nature is taken up with volumes and volumes of bridge laws.
I say there are no such bridge laws, or, more cautiously, we have no reason to assume them. But without the bridge laws, the distribution functions have no explanatory power. Thus our chief motivation for believing in them vanishes, and rightly so. The distribution functions play primarily an organizing role. They cannot be seen; they cause nothing; and like many other properties of convenience, we have no idea how to apply them outside the controlled conditions of the laboratory, where real life mimics explanatory models. What is the distribution function for the molecules in this room? Or the value of the electric field vector in the region just at the tip of my pencil? These questions are queer. They are queer because they are questions with no answers. They ask about properties that only objects in models have, and not real objects in real places.
I think we are often misled by a piece of backwards reasoning here. Sometimes for a given model, it is possible to contrive (or to find) a real situation in which the principal features relevant to the phenomenology are just the features mentioned in the model, and no others. Low density helium, for example, is an almost ideal gas from the point of view of the billiard ball model of statistical mechanics. In these cases, we are inclined to think of the model as an exact replica of reality, and to attribute to the objects modelled not only the genuine properties of the model, but also the properties of convenience. By continuity, we then argue, the properties of convenience must apply to more complex cases as well. But this is just backwards. With a good many abstract theoretical properties, we have no grounds for assigning them to complex, realistic cases. By continuity, they do not apply to the ideal cases either.
Returning to models, it may help to recall a disagreement
156
between Mary Hesse11
and Wilfrid Sellars.12
I share Sellars's stress on the relations among properties, for the point of the kind of models I am interested in is to bring the phenomenon under the equations of the theory. But Sellars and I are opposed over realism. He sees that phenomenological laws are hard to get right. If we want regular behaviour, the description of the circumstances must grow more and more complicated, the laws have less and less generality, and our statements of them will never be exceptionless. Fundamental laws, by contrast, are simple, general, and without exception. Hence for Sellars they are the basic truths of nature.
In opposition to Sellars, I have been arguing that their generality and exceptionlessness is mere appearance, appearance which arises from focusing too much on the second stage of theory entry. The fundamental equations may be true of the objects in the model, but that is because the models are constructed that way. To use the language I introduced in the last essay, when we present a model of a phenomenon, we prepare the description of the phenomenon in just the right way to make a law apply to it.
The problem for realism is the first stage of theory entry. If the models matched up one-to-one, or at least roughly
157
so, with the situations we study, the laws which govern the model could be presumed to apply to the real situations as well. But models are almost never realistic in the first sense; and I have been arguing, that is crucial to how physics works. Different incompatible models are used for different purposes; this adds, rather than detracts, from the power of the theory. We have had many examples already but let me quote one more text describing the variety of treatments available for lasers:
A number of authors have treated idealized interacting systems as models for lasers. Extensive studies have been carried out by Lax, Scully and Lamb, Haken, Sauerman, and others. Soluble models have been examined by Schwable and Therring. Several simplified dynamical models for devices of various sorts are given in the last chapter of Louisell's book.13
And so on.
There has been a lot of interest in models among
philosophers of science lately. It will help to compare the use I make of
models with other accounts. First, Redhead and Cushing: both Michael Redhead14
and James Cushing15 have recently done very nice
investigations of models in mathematical physics, particularly in quantum
mechanics and in quantum field theory. Both are primarily concerned not with
158
correspondence which simulacra
share with both
Secondly, the semantical view of theories: on the simulacrum account, models are essential to theory. Without them there is just abstract mathematical structure, formulae with holes in them, bearing no relation to reality. Schroedinger's equation, even coupled with principles which tell what Hamiltonians to use for square-well potentials, two-body Coulomb interactions, and the like, does not constitute a theory of anything. To have a theory of the ruby laser, or of bonding in a benzene molecule, one must have models for those phenomena which tie them to descriptions in the mathematical theory. In short, on the simulacrum account the model is the theory of the phenomenon. This sounds very much like the semantic view of theories, developed by Suppes16 and Sneed17 and van Fraassen.18 But the emphasis is quite different. At this stage I think the formal set-theoretic apparatus would obscure rather than clarify my central points. It is easiest to see this by contrasting the points I want to make with the use to which van Fraassen puts the semantic view in The Scientific Image.19
Van Fraassen holds that we are only entitled to believe in what we can observe, and that we must remain agnostic about theoretical claims which we cannot confirm by observation. This leads him to require that only the observable substructure of models permitted by the laws of a theory should map onto the structure of the situations modelled. Only that part of a theory which is supposed to represent observable facts, and not the parts that represent theoretical facts, need be an accurate representation of how things really are.
Van Fraassen's book takes a firm stand against realism. Sellars, I have mentioned, is a profound realist. But they
159
have in common a surprising respect for theory. Both expect that theories will get the facts right about the observable phenomena around us. For van Fraassen, the theoretical claims of a good theory need not match reality, but the claims about observables should. In a good theory, the observable substructure prescribed by the theory should match the structure of reality. This is not how I see good theories working. The observational consequences of the theory may be a rough match to what we suppose to be true, but they are generally not the best we can do. If we aim for descriptive adequacy, and do not care about the tidy organization of phenomena, we can write better phenomenological laws than those a theory can produce. This is what I have tried to show, beginning with Truth Doesn't Explain Much and ending with the prepared, but inaccurate descriptions discussed in the last essay.
There is also a second important difference with van Fraassen that does not fit readily into the semantic formalism. I have talked about observational substructures in order to contrast my views with van Fraassen's. But unlike van Fraassen, I am not concerned exclusively with what can be observed. I believe in theoretical entities and in causal processes as well. The admission of theoretical entities makes my view much closer to Sellars than it earlier sounded. All sorts of unobservable things are at work in the world, and even if we want to predict only observable outcomes, we will still have to look to their unobservable causes to get the right answers.
I want to focus on the details of what actually happens in concrete situations, whether these situations involve theoretical entities or not, and how these differ from what would happen if even the best of our fundamental laws played out their consequences rigorously. In fact, the simulacrum account makes the stronger claim: it usually does not make sense to talk of the fundamental laws of nature playing out their consequences in reality. For the kind of antecedent situations that fall under the fundamental laws are generally the fictional situations of a model, prepared for the needs of the theory, and not the blousy situations of reality. I do not mean that there could never be situations to which the fundamental laws apply. That is only precluded if the theory employs properties or arrangements which are pure fictions, as I think classical statistical mechanics does. One may occur by accident, or, more likely, we may be able to construct one in a very carefully controlled experiment, but nature is generally not obliging enough to supply them freely.
Let me repeat a point I have made often before. If we are going to argue from the success of theory to the truth of theoretical laws, we had better have a large number and a wide variety of cases. A handful of careful experiments will not do; what leads to conviction is the widespread application of theory, the application to lasers, and to transistors, and to tens of thousands of other real devices. Realists need these examples, application after application, to make their case. But these examples do not have the right structure to support the realist thesis. For the laws do not literally apply to them.
The simulacrum account is not a formal account. It says that
we lay out a model, and within the model we derive various laws which match
more or less well with bits of phenomenological behaviour. But even inside the
model, derivation is not what the D-N account would have it be, and I do not
have any clear alternative. This is partly because I do not know how to treat
causality. The best theoretical treatments get right a significant number of
phenomenological laws. But they must also tell the right causal stories.
Frequently a model which is ideal for one activity is ill-suited to the other,
and often, once the causal principles are understood from a simple model, they
are just imported into more complex models which cover a wider variety of
behaviour. For example, Richard Feynman, when he deals with light refraction in
Volume II of his famous
We want now to discuss the phenomenon of the refraction of light . . . by dense materials. In chapter 31 of Volume I we discussed a theory of the index of refraction, but because of our limited mathematical abilities at that time, we had to restrict ourselves to finding the index only for materials of low density, like gases. The physical principles that produced the index were, however, made clear . . . Now, however,
161
we will find that it is very easy to treat the problem by the use of differential equations. This method obscures the physical origin of the index (as coming from the re-radiated waves interfering with the original waves), but it makes the theory for dense materials much simpler.20
But what is it for a theoretical treatment to tell a causal story? How does Feynman's study of light in Volume I make clear the physical principles that produce refraction? I do not have an answer. I can tell you what Feynman does in Volume I, and it will be obvious that he succeeds in extracting a causal account from his model for low density materials. But I do not have a philosophic theory about how it is done. The emphasis on getting the causal story right is new for philosophers of science; and our old theories of explanation are not well-adapted to the job. We need a theory of explanation which shows the relationship between causal processes and the fundamental laws we use to study them, and neither my simulacrum account nor the traditional covering-law account are of much help.
Causal stories are not the only problem. Even if we want to derive only pure Humean facts of association, the D-N account will not do. We have seen two ways in which it fails in earlier chapters. First, from Essay 6, the fundamental laws which start a theoretical treatment frequently get corrected during the course of the derivation. Secondly, many treatments piece together laws from different theories and from different domains, in a way that also fails to be deductive. This is the theme of Essay 3.
These are problems for any of our existing theories of explanation, and nothing I have said about simulacra helps to solve them. Simulacra do a different job. In general, nature does not prepare situations to fit the kinds of mathematical theories we hanker for. We construct both the theories and the objects to which they apply, then match them piecemeal onto real situations, derivingsometimes with great precisiona bit of what happens, but generally not getting all the facts straight at once. The fundamental laws do not govern reality. What they govern has only the appearance of reality and the appearance is far tidier and more readily regimented than reality itself.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1605
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved