| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
EXTREME RELATIVE
Fie ![]() si functia
si functia ![]() .
.
Definitia V.3.1 (punct de extrem local)
Punctul x0IA se numeste
punct de extrem local (relativ) al
functiei f, daca ![]() a.i.
a.i. ![]() , diferenta
, diferenta
![]() (1)
(1)
pastreaza
semn constant ![]() .
.
Daca ![]() se spune ca x0 este punct de maxim (minim) local al functiei
f.
se spune ca x0 este punct de maxim (minim) local al functiei
f.
In continuare vom presupune ca A este o multime deschisa.
Definitia V.3.2 (punct critic)
Punctul x0IA se numeste
punct critic al functiei ![]() , daca f
este diferentiabila in x0 si
, daca f
este diferentiabila in x0 si ![]() (functionala liniara identic nula), adica
(functionala liniara identic nula), adica ![]() .
.
Teorema V.3.3 (Fermat)
Fie ![]() si x0IA. Daca x0 este punct de extrem local al functiei f si f
este diferentiabila in x0 atunci x0 este punct critic al
functiei f.
si x0IA. Daca x0 este punct de extrem local al functiei f si f
este diferentiabila in x0 atunci x0 este punct critic al
functiei f.
Demonstratie:
Presupunem ca x0IA este un
punct de maxim local al functiei f, deci ![]() a.i.
a.i. ![]() , diferenta
, diferenta
![]() .
.
Deoarece ![]() si A este o multime deschisa,
si A este o multime deschisa, ![]() . Fie
. Fie ![]() , h¹0Rp si
, h¹0Rp si ![]() . Atunci,
. Atunci, ![]() punctul
punctul ![]() , deci
putem defini functia
, deci
putem defini functia
![]() prin
prin ![]() . Cum
pentru
. Cum
pentru ![]()
![]() , rezulta ca t=0 este un punct de maxim local al functiei g si deci,
conform Teoremei lui Fermat (pentru functii reale de o variabila reala),
, rezulta ca t=0 este un punct de maxim local al functiei g si deci,
conform Teoremei lui Fermat (pentru functii reale de o variabila reala), ![]() . Dar
. Dar
![]()
Cum ![]() , rezulta
ca
, rezulta
ca ![]() este
functionala liniara identic nula, deci x0 este un punct critic al
functiei f.
este
functionala liniara identic nula, deci x0 este un punct critic al
functiei f.
Observatia V.3.4
Conditia ca f sa fie diferentiabila in x0 si ![]() nu este suficienta pentru ca x0 sa
fie punct de extrem local al functiei f.
nu este suficienta pentru ca x0 sa
fie punct de extrem local al functiei f.
Intr-adevar, pentru functia ![]() , punctul
, punctul ![]() este punct critic, insa cum in orice
vecinatate
este punct critic, insa cum in orice
vecinatate ![]() puncte
pentru care
puncte
pentru care ![]() , cat si
puncte pentru care
, cat si
puncte pentru care ![]() , rezulta
ca p0 nu este un punct de extrem local.
, rezulta
ca p0 nu este un punct de extrem local.
Teorema V.3.5
Fie ![]() si x0IA. Daca x0 este punct de minim (maxim) local al functiei f,
atunci pentru
si x0IA. Daca x0 este punct de minim (maxim) local al functiei f,
atunci pentru ![]() ,
, ![]() (respectiv
(respectiv ![]() ).
).
Demonstratie:
Conform formulei lui Taylor-Young si Observatiei V.2.6, variatia
functiei f pe un disc ![]() se poate exprima sub formula:
se poate exprima sub formula:
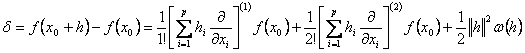 (2)
(2)
unde
w este continua si nula in ![]() .
.
Deoarece x0 este punct de minim local al functiei f:
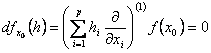
si
din relatia (2) devine pentru ![]() :
:
![]() (3)
(3)
Fie hIS, unde S este sfera unitate.
Atunci, ![]() si din (3) rezulta
si din (3) rezulta
![]()
adica
![]()
![]() (4)
(4)
Trecand la limita in (4) pentru t 0, rezulta ca ![]() .
.
Fie ![]() si
si ![]() .
.
Deoarece 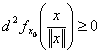 si
si 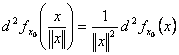 , rezulta
, rezulta ![]() .
.
Analog se demonstreaza cazul cand x0 este punct de maxim local.
Observatia V.3.6
Reciproca Teoremei V.3.5 nu este adevarata.
In cazul cand ![]() este nedegenerata (adica matricea Hesse, Hj(x0),
este nesingulara), se poate da o conditie suficienta pentru ca x0 sa
fie punct de extrem local.
este nedegenerata (adica matricea Hesse, Hj(x0),
este nesingulara), se poate da o conditie suficienta pentru ca x0 sa
fie punct de extrem local.
Teorema V.3.7
Fie ![]() si x0IA un punct critic al functiei f.
si x0IA un punct critic al functiei f.
Daca forma patrata ![]() este pozitiv (negativ) definita, atunci x0
este punct de minim (maxim) local al functiei f.
este pozitiv (negativ) definita, atunci x0
este punct de minim (maxim) local al functiei f.
Demonstratie:
Cum am vazut ca formula lui Taylor-Young ne permite sa exprimam
variatia functiei f pe un disc ![]() sub forma:
sub forma:
![]() (5)
(5)
Sa presupunem ca ![]() este pozitiv definita, deci
este pozitiv definita, deci ![]() pentru
pentru ![]() .
.
Sa aratam ca atunci m>0 a.i. ![]() are loc:
are loc:
![]() (6)
(6)
Observam ca functia ![]() , definita
prin:
, definita
prin:
![]()
pentru
![]() este continua pe Rp.
este continua pe Rp.
Deoarece ![]() este continua pe S si S este compacta, rezulta
ca
este continua pe S si S este compacta, rezulta
ca ![]() este marginita pe S si isi atinge marginile.
este marginita pe S si isi atinge marginile.
Fie ![]() si
si ![]() a.i.
a.i. ![]() .
.
Cum ![]() este pozitiv definita si
este pozitiv definita si ![]() , rezulta
ca m>0.
, rezulta
ca m>0.
Atunci, ![]() si prin urmare
si prin urmare 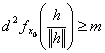 .
.
Dar 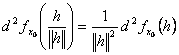
si
din inegalitatea ![]() rezulta ca
rezulta ca ![]() .
.
Cum inegalitatea este verificata si pentru ![]() , relatia
(6) este demonstrata. Din relatiile (5) si (6) rezulta ca pentru
, relatia
(6) este demonstrata. Din relatiile (5) si (6) rezulta ca pentru ![]()
![]() (7)
(7)
Deoarece w este continua si nula in ![]() ,
, ![]() a.i.
a.i. 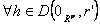 are loc:
are loc:
![]() (8)
(8)
Din (7) si (8) rezulta ca pentru 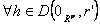
![]()
deci x0 este punct de minim local al functiei f.
Cazul cand ![]() este negativ definita se trateaza analog.
este negativ definita se trateaza analog.
Observatia V.3.8
Pentru a arata ca un punct stationar x0 al functiei ![]() , este un
punct de extrem local al functiei f, este suficient sa aratam ca:
, este un
punct de extrem local al functiei f, este suficient sa aratam ca:
a) ![]() (respectiv
(respectiv ![]() ),
), ![]() ;
;
b) ![]() este nesingulara.
este nesingulara.
Teorema V.3.9
Fie ![]() . Daca x0IA este un punct stationar al functiei f si
. Daca x0IA este un punct stationar al functiei f si ![]() nu este definita, atunci x0 nu este
punct de extrem local al functiei f.
nu este definita, atunci x0 nu este
punct de extrem local al functiei f.
Demonstratie:
Daca ![]() este nedefinita, atunci
este nedefinita, atunci ![]() a.i.
a.i. ![]() si
si ![]() .
.
Cum intr-un disc ![]() variatia lui f este data prin:
variatia lui f este data prin:
![]()
rezulta
ca d are acelasi semn cu ![]() , care,
prin ipoteza, nu are semn constant. Deci x0 nu este punct de extrem
local.
, care,
prin ipoteza, nu are semn constant. Deci x0 nu este punct de extrem
local.
Pentru aplicatii sunt utile:
Propozitia V.3.10 (Teorema lui Sylvester)
Fie forma patratica ![]() , care are
in baza canonica
, care are
in baza canonica ![]() matricea
matricea ![]() sunt minorii principali de ordinul i ai
matricei FB
sunt minorii principali de ordinul i ai
matricei FB
Urmatoarele afirmatii sunt adevarate:
i) F este pozitiv (negativ) definita;
ii)
![]() (respectiv,
(respectiv, ![]() .
.
Propozitia V.3.11
Conditia necesara si suficienta ca forma patratica ![]() sa fie
pozitiv (negativ) definita este ca matricea formei patratice sa aiba toate
valorile proprii strict pozitive (strict negative).
sa fie
pozitiv (negativ) definita este ca matricea formei patratice sa aiba toate
valorile proprii strict pozitive (strict negative).
Din cele prezentate mai sus
rezulta regula practica de determinare a punctelor de extrem relativ ale unei
functii ![]() .
.
i) Punctele de extrem local se afla, conform teoremei V.3.3. printre solutiile sistemului:
![]() (9)
(9)
ii)
Daca x0IA este un punct critic al functiei f, atunci se verifica daca forma
patratica ![]() este pozitiv (negativ) definita sau nu este
definita.
este pozitiv (negativ) definita sau nu este
definita.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1610
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved