| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
Campul gravific
Un punct material P situat pe suprafata Pamantului este supus actiunii unor forte multiple:
v
gravitatia sau forta de atractie 
indreptata spre centrul de masa ala Pamantuui;
v
forta centrifuga 
provocata de miscarea de rotatie a Pamantului si care este indreptata catre exteriorul
Pamantului;
v fortele de atractie exercitate de alte corpuri ceresti (dintre care fortele de atractie ale Soarelui, datorita masei sale si, respectiv ale Lunii, datorita apropierii sale de Pamant, sunt cele mai impotante). Se poate arata ca:
(2.7)
Datorita acestei relatii, punctele, obiectele si persoanele isi mentin
pozitia pe Pamant. Asupra punctului P actioneaza, in principiu, toate
planetele din Univers, dar pe masura ce distanta
creste, se micsoreaza forta de atractie a acestora. De aceea, de regula se iau in consideratie doar:
este forta de atractie a Soarelui;
este forta de atractie a Lunii.
Suma tuturor fortelor care actioneaza asupra
punctului P se numeste gravitate 
sau greutate:
+ + . 
(2.8)
Pamantul este un corp elastic, care isi modifica forma in timp, diametrul sau ( 13000 km) are variatii, in zonele cele mai elastice, de maxim 30 cm. Abordarea acestei probleme fiind foarte dificila, in Geodezie Pamantul se considera un corp rigid.
Sensul gravitatii este sensul directiei firului cu plumb. Toate instrumentele
(topografice, geodezice etc.) sunt orientate in timpul masurarii dupa directia
gravitatii, prin calare. Deoarece Pamantul are structura
diferita, fortele 
si nu sunt paralele pe suprafata Pamantului. Dupa un calaj parfect, axa principala a
instrumentului notata, de obicei, cu V - V este orientata dupa (verticala locului sau a punctului de statie).
Regiunea din spatiu in care se extinde influenta complexa a atractiei gravitationale si a rotatiei Pamantului constituie campul gravitatii sau campul gravific (Constantinescu, 1964, Ghitau, 1983).
Deoarece activitatea geodezica (cu toate ramurile sale - topografia, cadastrul s.a.) se desfasoara in campul gravific, fiind influentata efectiv de acesta, este necesara studierea (teoretica) a componentelor sale. Din aceste studii vor rezulta insa concluzii deosebit de importante pentru geodezia aplicativa.
1.
Forta de atractie (gravitatia). Potrivit cu
legea atractiei universale a lui Newton forta de atractie reciproca 
dintre 2 mase
punctiforme m1 si m2, situate la distanta d este data de
relatia:
(2.9)
unde - d0 este versorul directiei care uneste masele m1 si m2;
- G este constanta atractiei universale. Recomandarile Asociatiei Internationale de Geodezie (AIG) din anul 1995 prevad pentru aceasta constanta valoarea:
G = (6672,59 0,30) 10-14 m3s-2kg-1 (2.10)
in Sistemul International (SI).
Constanta atractiei universale este numeric egala cu forta cu care se atrag intre ele doua corpuri cu masele egale cu unitatea, situate unul fata de celalalt la o distanta egala cu unitatea.
Aceste notiuni indica faptul ca dimensiunile, respectiv masa corpului considerat (de exemplu un punct geodezic situat pe suprafata Pamantului) sunt neglijabile fata de dimensiunile, respectiv masa sistemelor cu care acel corp este in interactiune (Pamantul in exemplul considerat).
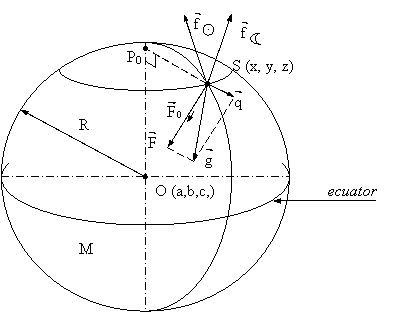
Fig. 2.5. Fortele care actioneaza asupra punctelor (in ipoteza Pamant sfera).
Daca se introduc urmatoarele aproximatii:
Ø Pamantul este un corp rigid;
Ø forma Pamantului este sferica;
Ø Pamantul
este omogen de densitate fie
se poate concluziona ca masa Pamantului poate fi concentrata in centrul sferei O (punct greu). Aceste aproximatii se pot scrie si sub forma:
, (2.11)
de unde:
. (2.12)
Analog cu (2.9) se poate scrie:
(2.13)
fiind versorul fortei de atractie 
Semnul ( ) in
formula (2.13) este datorat sensului diferit al fortei de atractie in raport cu sensul axelor
de coordonate.
Forta de atractie este descrisa complet prin proiectiile sale:
(2.14)
Acestea se obtin cu relatiile cunoscute din geometria analitica:
(2.15)
si analog:
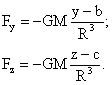(2.16)
Marimea GM este denumita constanta gravitationala geocentrica, pentru care recomandarile AIG 1980 prevad:
GM = (39860047 107m3s-2 , (2.17)
in anul 1995:
GM = (398600441,8 106m3s-2. (2.18)
Se pot deduce unele valori cu caracter de orientare generala:
Ø masa Pamantului M:
M 5 1024 kg (2.19)
si, in ipoteza formei sferice a Pamantului cu
R 6378 103 m (pentru latitudinea B = 45 ); (2.20)
Ø densitatea medie a Pamantului:
kgm-3. (2.21)
In ipoteza formei elipsoidale a Pamantului rezulta densitatea medie:
kgm-3
Caracterul aproximativ al formulei (2.12) este generat de imprecizia cu care se cunosc sau se pot determina elementele componente. Aceasta remarca este valabila in mod deosebit pentru masa Pamantului, notata M, care depinde in primul rand de densitatea r a acestuia. La randul sau, densitatea maselor este o functie de mai multi parametri, dintre care cel mai important este adancimea fata de suprafata terestra.
Fara a intra in detaliile care intereseaza in mod deosebit geofizica se prezinta unele informatii privind variatia in marimea densitatii ce se pot urmari in figura urmatoare (Socolescu s.a., 1975).
Fig. 2.6. Variatia densitatii
catre interiorul Pamantului.
Intr-o prima zonare, de ordinul I, structura interna a Pamantului este reprezentata de 3 geosfere: scoarta, mantaua si nucleul. Limitele dintre aceste sfere se numesc discontinuitati de ordinul I: discontinuitatea Mohorovii (denumita curent discontinuitatea Moho) si respectiv discontinuitatea Oldham ori Gutenberg. Se apreciaza ca discontinuitatea Moho se afla la o distanta medie de 33 km, punctandu-se, insa, si variatiile concave de 40-50 km, sub blocurile continentale, si ondulatiile convexe de pana la 5 km, sub zonele oceanice.
Scoarta terestra este constituita din doua strate: stratul bazaltic continuu si stratul granitic discontinuu, ambele de grosimi variabile. Deasupra acestor strate urmeaza depozitele stratului sedimentar, care are, de asemenea, grosimi variabile.
Pentru stratul granitic se accepta densitatea rg = 2,7 g/cm3, iar pentru calcule mai precise 2,67 g/cm3.
In continuare pot fi mentionate si subimpartiri, respectiv discontinuitati de ordinul II, a caror pozitionare pe verticala in raport cu scoarta terestra nu este unanim acceptata in lucrarile de specialitate.
2. Forta centrifuga.
Datorita
miscarii de rotatie a Pamantului in jurul axei sale, punctul P este supus unei
forte centrifuge 
care este situata intr-un plan paralel cu
planul ecuatorului terestru al punctului P.
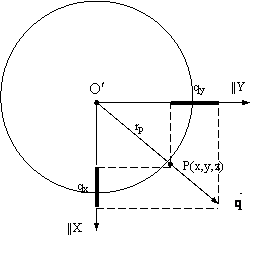
Fig. 2.7. Forta centrifuga.
Particularizand expresia cunoscuta, din mecanica, pentru forta centrifuga in cazul punctului P, cu masa egala cu unitatea, in functie de viteza liniara pe traiectorie, v, se obtine:
(2.23)
Folosind relatia de legatura dintre viteza liniara si viteza unghiulara w
v = rpw , (2.24)
rezulta
(2.25)
unde - rp este raza paralelului;
este versorul razei paralelului;
w este viteza de rotatie a Pamantului.
Viteza unghiulara medie, in cazul Pamantului, recomandata de AIG 1980 este:
w 10-11 rad s-1. (2.26)
Din relatia (2.26) se observa ca forta centrifuga este variabila pe suprafata Pamantului, avand o valoare maxima pentru punctele situate pe ecuator si fiind nula pentru poli, unde r = 0. Pentru a puncta ordinul de marime, se poate retine raportul:
. (2.27)
Componentele fortei centrifuge 
vor
fi:
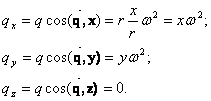(2.28)
3. Gravitatea (greutatea). Asa cum s-a aratat anterior, gravitatea este componenta tuturor fortelor care actioneaza asupra punctului P (relatia (2.8)). Daca ne marginim in aproximatia primelor doua forte (principale ca marime) se poate scrie:
(2.29)
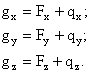(2.30)
4. Potentialul gravitatii. Laplace (sec. XVIII) a introdus notiunea de potential, ce poate fi definit atat matematic cat si prin semnificatiile sale fizice.
Potentialul este o functie continua si derivabila, atasata unui camp de forte, ale carei derivate, dupa o directie oarecare (x, y, z, s) sunt egale cu componentele campului respectiv pe directia considerata.
Deoarece am admis aproximatia:
(2.31)
se poate scrie: W = V + Q, (2.32)
unde W = potentialul gravitatii; V = potentialul de atractie (al fortei de atractie); Q = potentialul fortei centrifuge.
4.1. Potentialul de atractie (newtonian). Potentialul campului fortei de atractie (al gravitatiei) numit si potential de atractie sau potentialul newtonian, se noteaza cu V si are expresia:
(2.33)
in cazul aproximtiei formei sferice a Pamantului.
Prin particularizare, in cazul punctului atras
de masa egala cu unitatea, potentialul de atractie al unui punct sursa de masa
m, situat la distanta 
, va fi:
(2.34)
Pentru demonstrarea relatiei (2.23) se exprima raza R in raport de coordonatele punctelor P (x, z, y) si respectiv O (a, b, c) din Fig. 2.5:
(2.35)
Derivata partiala in raport de x a functiei (2.33) este:
(2.36)
Din (2.35) rezulta:
si prin urmare:
astfel incat relatia (2.36) devine:
(2.38)
si analog
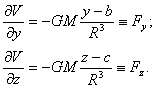(2.39)
Ultimele trei relatii reprezinta exprimarea matematica a definitiei date pentru potentialul de atractie.
Semnificatia fizica a potentialului. Elementul diferential dV al potentialului de atractie, in cazul a doua puncte infinit apropiate P(x,y,z) si P(x + Dx, y + Dy, z + Dz) de mase egale cu unitatea, situate la distanta ds este:
(2.40)
unde
(2.41)
unde 
reprezinta o directie oarecare din spatiul garafic.
Considerand relatiile:
(2.42)
si
(2.43)
rezulta
(2.44)
adica
sau mai prescurtat:
(2.46)
unde 
reprezinta
proiectia gravitatiei pe directia s oarecare.
Aceasta relatie scrisa sub forma: 
, (2.47)
reprezinta proprietatea fundamentala a scalarului potential (in general) si anume: derivata potentialului dupa o anumita directie este egala cu proiectia campului dupa acea directie. Relatiile (2.42) sunt, prin urmare, cazuri particulare ale formulei (2.48).
Din expresia (2.46) rezulta ca elementul infinit mic de
potential gravitational dV reprezinta lucrul mecanic pe care il efectueaza
forta de atractie 
pentru deplasarea
punctului P, de masa egala cu unitatea, in punctul R, situat la distanta ds.
Observatie. Pentru doua puncte P (de masa egala cu unitatea) si respectiv S (punct sursa, de masa m), situate la o distanta D oarecare, potentialul campului de atractie va fi reprezentat de lucrul mecanic:
(2.48)
Presupunand ca P ¥ (D ¥), atunci VP 0, conform cu Observtia de sub
relatia (2.34), rezulta prin urmare : 
(2.49)
Potentialul campului fortei de atractie intr-un punct este egal cu lucrul mecanic efectuat de forta de atractie pentru deplasarea unitatii de masa de la infinit in punctul dat.
Aceasta proprietate este specifica potentialului gravitational, si nu in general; in particular, aceasta nu este valabila nici pentru potentialul campului gravitatii W.
4.2. Potentialul fortei centrifuge. Potentialul din care deriva forta centrifuga este reprezentat de urmatoarea functie:
(2.50)
In adevar, se observa ca:
(2.51)
4.3. Potentialul gravitatii. In aproximatia folosita:
W = V +Q, (2.52)
rezulta 
(2.53)
(2.54)
5. Gravitatea (greutatea) masurata (g). Asa cum s-a aratat anterior, gravitatea este componenta tuturor fortelor care actioneaza asupra punctului P. In acest manual, se vor lua in consideratie doar componentele principale mentionate anterior.
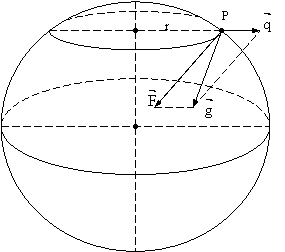
Greutatea 
(in ipoteza formei sferice a Pamantului).
(2.55)
Lucrandu-se cu puncte de masa egala cu unitatea, gravitatea este numeric egala cu acceleratia sa. Unitatea de masura in sistemul CGS este galul (1 gal = 1 cms-2), denumire adoptata in memoria marelui invatat italian Galileo Galilei. Deoarece la pol marimea gravitatiei este aprximativ egala cu 983 gal, iar la ecuator 978 gal ar rezulta o variatie mult prea putin semnificativa in aceasta unitate de masura. De aceea in geodezia fizica se lucreaza in miligali (1 mgal = 10-3 gal), instrumentele de masura actuale avand o precizie de ordinul a 0,01 mgal sau chiar si mai buna.
Marimile care formeaza obiectul determinarilor gravimetrice sunt:
acceleratia gravitatii g;
variatii ale acceleratiei gravitatii Dg;
derivate de ordinul 2 ale geopotentialului Wyy - Wxx, Wxy - Wyz, Wzz.
Asa cum s-a mentionat, acceleratia gravitatii prezinta variatii locale si temporale, care depind de o mutitudine de factori, dintre care cei mai importanti sunt urmatorii:
Ø Forma Pamantului. Considerandu-se valorile normale ale acceleratiei gravitatii (care va fi definita ulterior, in acest capitol):
g mgal; g = 983218,66 mgal, (2.56)
se inregistreaza o variatie intre ecuator si pol de aproximativ + 5185,96 mgal.
Ø Distributia si densitatea maselor in interiorul Pamantului. Variatiile de gravitate generate de acesti factori se pot constata prin masuratori gravimetrice efectuate pe apa si apoi, in apropiere, pe uscat, respectiv pe o vale si pe dealul apropiat etc. Diferentele dintre valorile masurate si reduse la suprafata geoidului, notate g si valorile normale g ale acceleratiei gravitatii (considerate pe elipsoid) nu sunt constante, diferentele maxime g - g putand atinge valori de ordinul 200 mgal.
Ø Influentele diverse exercitate de corpurile ceresti. Variatiile temporale, inregistrate in puncte stationare, datorate in mod deosebit Lunii si Soarelui, sunt mai mici de 0,3 mgal.
Ø Gradientul vertical al gravitatii. Variatia gravitatii in functie de cota H este de aproximativ 0,0848 mgal/m.
Ø Modificari in potentialul gravitatii. Acestea sunt datorate circuitului apei in atmosfera, miscarilor maselor in interiorul Pamantului, deplasarilor polului mecanic s.a., influenta lor ajungand pentru un punct dat, la marimi de ordinul a 0,01 mgal pentru un deceniu.
Dupa cum se vede, variatiile gravitatii sunt caracterizate prin ordine de marime cu totul diferite si, ca atare, aparatele si metodele de masurare trebuie sa asigure o precizie corespunzatoare acestei variatii, in functie de scopul urmarit.
In prezent determinarile gravimetrice au atins parametri foarte inalti de precizie:
masuratorile in puncte stationare, in conditii deosebite de lucru in laborator, destinate etalonarilor sau determinarilor mareelor terestre au precizia situata sub limita 0,001 mgal;
masuratorile de teren sunt caracterizate, in general, de erori cuprinse intre 0,01 mgal si 0,05 mgal. In unele publicatii se comunica si pentru astfel de lucrari obtinerea unei precizii foarte inalte, de circa 0,003 mgal, realizata cu aparate perfectionate.
Determinarile acceleratiei gravitatii in puncte stationare (puncte de baza), efectuate independent, se numesc determinari absolute, iar determinarile de variatii ale acceleratiei gravitatii, in raport de un punct de baza se numesc determinari relative. Masuratorile de gravitate se bazeaza in prezent, pe utilizarea fenomenelor de oscilatie, de cadere libera a corpurilor si de modificare a echilibrului unui sistem deformabil, existand urmatoarea clasificare uzuala:
Metoda dinamica, in care masurarea gravitatii se realizeaza prin urmarirea in timp a unor corpuri in miscare. Aparatul clasic pentru acest grup de metode este pendulul. Dupa masurarea perioadei de oscilatie si a altor parametri necesari, se calculeaza valoarea gravitatii in punctul de observatie.
In ultimele doua decenii au fost perfectionate si metode de determinari absolute ale acceleratiei gravitatii, bazate pe legea miscarii rectilinii uniform accelerate in caderea libera a corpurilor.
Metoda statica, folosita la evaluarea variatiei gravitatii din punct in punct sau in timp, pentru un acelasi loc, consta in examinarea starii de echilibru a unui sistem deformabil, asupra caruia actioneaza simultan gravitatea (ca forta independenta sau intr-un cuplu de forte) si un factor antagonist de natura elastica (forta sau cuplu de forte). Instrumentul tipic pentru aceasta metoda este gravimetrul static.
Determinarea unor derivate de ordinul 2 ale potentialului se bazeaza, in principiu, pe utilizarea unei metode statice, care consta in urmarirea starii de echilibru a unei parghii suspendata de un fir de torsiune. Actiunea este reprezentata de un cuplu gravitational (in care intervin derivatele de ordinul 2 ale potentialului), iar reactiunea de cuplul de torsiune al firului de suspensie. Presupunand constant coeficientul de torsiune al firului sau cunoscand legea sa de variatie, modificarea starii de echilibru dintr-un punct in altul este datorata, in primul rand, variatiilor derivatelor de ordinul 2 ale potentialului. Acestea au dimensiunile unui gradient, de exemplu:
gradient orizontal, in directia x al gravitatii.
Gradientul vertical al gravitatii Wzz nu este masurabil, putand fi determinat doar indirect. Unitatea de masura pentru aceste derivate de ordinul 2 ale potentialului este reprezentata de variatia de 0,1 mgal pe distanta de 1 km:
(2.57)
fiind numita Etvs, in onoarea savantului maghiar care a realizat aparatul pentru masurarea acestei marimi, numit balanta de torsiune.
5.1. Determinari absolute de acceleratie a gravitatii (g)
Pendulul matematic este reprezentat de un punct material suspendat intr-un punct fix (prin intermediul unui fir inextensibil de masa neglijabila) care executa o miscare de oscilatie in planul vertical al punctului de suspensie, exclusiv sub influenta gravitatii (Fig. 2.9).
Continutul acestui capitol fiind relativ independent, in raport cu celelalte capitole, se vor folosi notatii care in restul manualului au alta semnificatie, deoarece notiunile respective nu sunt utilizate simultan. Astfel, se vor folosi ca notatii principale:
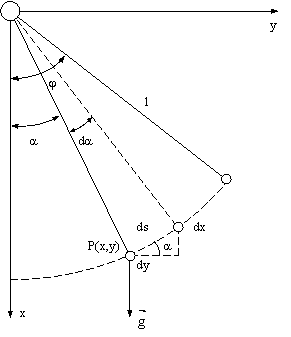
Fig. 2.9. Pendulul matematic.
m - masa pendulului;
j - amplitudinea, respectiv unghiul care caracterizeaza pozitia extrema a pendului;
a - elongatia, respectiv unghiul care caracterizeaza pozitia curenta, la un moment dat a pendulului;
T - perioada completa a oscilatiei, respectiv timpul necesar pendulului pentru a trece dintr-o pozitie extrema (- j) in cealalta (+ j) si inapoi;
l - lungimea pendului.
Se poate demonstra ca perioada T a pendulului matematic poate fi exprimata in cadrul amplitudinilor j mici, cu formula:
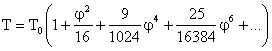(2.58)
unde j trebuie exprimat in radiani, iar T0 - perioada completa pentru amplitudini infinit mici (j
(2.59)
Pendulul matematic este imposibil de realizat practic, avand in definitia sa ipoteze simplificatoare, care nu au echivalent in realitate.
Pendulul fizic este reprezentat de un corp material, nedeformabil, care oscileaza in vid, in jurul unei axe fixe, orizontale, sub influenta gravitatii. Conditia de oscilatie a pendulului fizic este ca axa de suspensie sa nu treaca prin centrul de greutate G (xG, yG) al corpului, ci sa fie situata deasupra lui (Fig. 2.10).
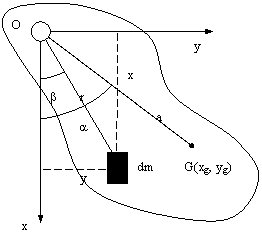
Fig. 2.10. Pendulul fizic.
Se noteaza cu Lr lungimea redusa a pendulului fizic:
(2.60)
unde k este o valoare medie pentru distanta r dintre un punct curent al elementului de masa dm si centrul de greutate G. Pastrand si ipoteza amplitudinilor mici, se poate demonstra ca perioada pendulului fizic se exprima analog cu (2.59):
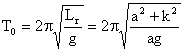(2.61)
Determinarea constantelor a si k este dificila si putin precisa, astfel incat expresiile de calcul ale acceleratiei gravitatii care le contin nu asigura precizia necesara.
Perioada T0 se poate determina cu mai multa exactitate, astfel incat in ipoteza cunoasterii lungimii reduse Lr, se ofera posibiliatea principiala pentru determinarea acceleratiei gravitatii:
(2.62)
Dificultatile de ordin practic rezida, in special, in
determinarea cu o precizie convenabila, a lungimii reduse. Pentru rezolvarea acestei probleme se presupune ca in acelasi punct se efectueaza simultan
si in conditii identice determinari gravimetrice cu un pendul cu lungimea
redusa 
cunoscuta.
Masurand, cu precizia necesara, cele doua perioade 
si 
se pot calcula, in
ipoteza g = constant, lungimea redusa a primului
pendul:
(2.63)
Pendulul reversibil este un pendul care are doua axe paralele de suspensie, respectiv de oscilatie, care sunt intersanjabile.
Perioada T a pendulului reversibil se determina cu relatia:
(2.64)
fiind dedusa in urmatoarele ipoteze, realizabile constructiv:
perioadele T1 si T2 corespondente celor doua pozitii de oscilatie, sunt mici, astfel incat (T1 - T2)
centrele de oscilatie sunt dispuse asimetric in raport cu centrul de greutate, astfel incat diferenta dintre distantele corespondente a1 si a2 este mare.
(2.65)
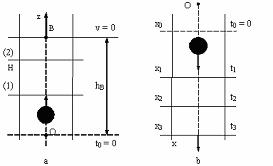
Fig. 2.11. Lansarea pe verticala si caderea libera, in vid, a corpurilor.
Deoarece in ecuatie intervin trei necunoscute x0, v0, g, pentru o rezolvare matematica sunt necesare trei determinari. Din acestea rezulta:
iar dupa eliminarea necunoscutei v0, se obtine valoarea acceleratiei gravitatii in functie de elementele cunoscute:
(2.66)
Deoarece in expresia de calcul intervin numai diferente de timp si spatiu, erorile de determinare sunt micsorate. In practica se efectueaza un numar n de determinari, prelucrarea rezultatelor realizandu-se prin metoda celor mai mici patrate.
Procedeul de determinare efectiv este realizat
in vid inaintat, pe o inaltimie de sub 1 m, cand masuratorile au loc in
laborator. Precizia anuntata este situata sub 
mgal (Groten
1980).
5.2. Masuratori relative de gravitate (dg Variatiile acceleratiei gravitatii sunt determinate cu ajutorul aparatelor pendulare si respectiv al gravimetrelor.
Determinari relative cu aparate pendulare. In punctele P1 (initial), unde acceleratia gravitatii g1 este cunoscuta si in punctul P2, unde urmeaza sa se determine g2 se masoara perioadele T1 si respectiv T2 cu un anumit pendul. Relatia (2.61) pentru aceste doua situatii fiind:
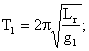
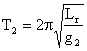(2.67)
se obtine marimea cautata: 
(2.68)
In relatia (2.68) nu intervine lungimea redusa Lr, ceea ce determina simplificari remarcabile in masuratorile absolute.
Principiile de constructie a gravimetrelor. Gravimetrele moderne sunt gravimetre mecanice, al caror sistem de functionare se bazeaza pe posibilitatea de constatare a unor modificari in starea de echilibru a unui sistem deformabil (resorturi, sisteme de resorturi sau sisteme de torsiune), in functie de variatiile acceleratiei gravitatii.
Variatia deformarii sistemului elastic (deci implicit variatia acceleratiei gravitatii) este pusa in evidenta de un sistem indicator. Exigentele de determinare cu un gravimetru sunt reflectate de erori de masurare de ordinul a 0,01 mgal sau si mai mici (erori relative mai mici de 1 10-8). Aceasta precizie de masurare deosebita este insotita si de alte calitati remarcabile: constructie robusta, greutate mica, usurinta de manipulare chiar in puncte greu accesibile si in conditii dificile de exploatare.
Una dintre clasificarile uzuale ale gravimetrelor este urmatoarea:
gravimetre neastatizate, care contin sisteme deformabile a caror variatie de la pozitia de echilibru este direct proportionala cu variatia gravitatii;
gravimetre astatizate, care sunt astfel realizate incat sa contina un element suplimentar (denumit labilizator) care intervine la modificarea starii de echilibru, adaugand actiunea sa la actiunea gravitatii.
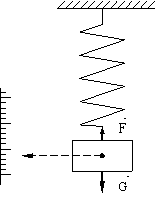
Fig. 2.12. Sistem neastatizat.
Intr-un punct in care se presupune un resort sprijinit de un suport actioneaza urmatoarele forte:
actiunea, reprezentata de greutatea sistemului: G = mg;
reactiunea, reprezentata de forta elastica a resortului, proportionala cu deformarea sa x:
F = Sx
Conditia de echilibru, intr-un punct dat, va fi prin urmare:
(2.69)
Din relatia anterioara rezulta modalitatea de functionare a unui gravimetru construit pe sistemul descris:
(2.70)
unde Dx = x2 - x1, valoare determinata pe o rigla gradata odata cu trecerea din punctul P1 in punctul P2.
Pentru a se obtine precizia de determinare 
este
necesar ca eroarea in determinrea citirilor x sa nu depaseasca valoarea:
(2.71)
Daca
m, rezulta 
mm, conditie
care este extrem de difcil de realizat in conditii de teren.
Sisteme astatizate. Pe langa amplificari exterioare exista si posibilitati de marire a sensibilitatii gravimetrelor pe cale interioara, prin asa-numitul proces de astatizare, in care intervine un element care are rolul de a accentua deformarea.
Se mentioneaza aici inca un criteriu de clasificare uzuala a gravimetrelor si anume:
gravimetre cu miscare de translatie;
gravimetre cu deformare de rotatie.
Expunerea principiilor de functionare a unor
asemenea sisteme gravimetrice depaseste cadrul manualului. Este de mentionat ca
sistemele astatizate sunt
caracterizate de erori absolute 
situate
sub 0,001mgal, fiind cele mai perfectionate
sisteme gravimetrice de teren.
5.3. Retele gravimetrice
Punctul fundamental in reteaua gravimetrica. Reteaua gravimetrica a tarii noastre are ca reper fundamental statia de pendul Surlari, din cadrul Observatorului geomagnetic al Academiei Romane, punctul gravimetric fiind cunoscut fie sub numele de Surlari, fie sub numele de Caldarusani. Determinarile au fost efectuate in anii 1947 si 1948 cu un aparat tetrapendular Askania, de catre M. Socolescu obtinandu-se valoarea 980542,90 mgl in sistemul vechi Potsdam (Khnen-Furtwngler) bazat pe masuratori cu aparate pendulare, efectuate intre anii 1898-1906.
In gravimetrie este de remarcat, mult mai pregnant decat in cazul triangulatiei sau nivelmentului, definirea unui sistem international de referinta, la care urmeaza sa se racordeze retelele nationale.
De mentionat ca la nivel international au intervenit modificari importante in intervalul de timp scurs.
=
981260 mgal. (2.72)
Astfel, la a XV-a Adunare generala a UIGG din anul 1971, desfasurata la Moscova, s-a hotarat adoptarea unui sistem international de referinta a carui denumire in limba engleza este International Gravity Standardization Net 1971 (IGSN71). Acest nou sistem de referinta, la care ar trebui racordate retelele gravimetrice nationale, inlocuieste sistemul Potsdam, fiind reprezentat de 1854 statii gravimetrice. Sistemul este caracterizat printr-o precizie de ordinul 0,1 mgal, chiar de 0,01 mgal.
Retelele gravimetrice pot fi clasificate in:
retele gravimetrice de sprijin;
retele gravimetrice de prospectiuni.
Dintre retelele gravimetrice de sprijin trebuie mentionata in primul rand reteaua gravimetrica internationala la care se racordeaza retelele nationale gravimetrice, sistemul international astfel creat avand o importanta deosebita in studierea formei si dimensiunilor Pamantului.
Liniile si bazele gravimetrice etalon au fost create de catre Uniunea Internationala de Geodezie si Geofizica pentru asigurarea unei bune racordari a lucrarilor gravimetrice internationale. Acestea au fost determinate cu cea mai mare precizie posibila si la ele se racordeaza lucrarile gravimetrice nationale.
Pentru
scopuri nationale, fiecare
mgal 
mgal. (2.73)
6. Gravitatea normala (g Pentru numeroase scopuri, geodezia foloseste, de foarte mult timp si notiunea de gravitate normala care se obtine prin calcul, cu un efort infinit mai mic decat gravitatea masurata. Formulele de calcul sunt recomandate de AIG la diferite intervale de timp. Astfel, in 1980 se recomanda:
g = 978032,7(1+0,0053024 sin2B - 0,00000058 sin22B), (2.74)
unde B este latitudinea punctului.
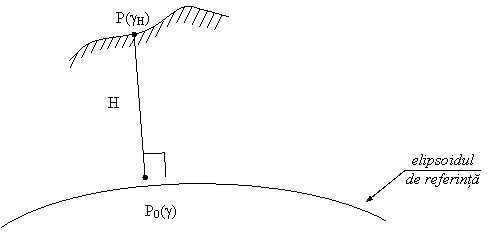
Fig. 2.13. Variatia gravitatii normale deasupra elipsoidului.
In geofizica si in geodezie se considera de multe ori ca intre suprafata elipsoidului si suprafata fizica este aer liber iar oamenii de stiinta au determinat o formula de calcul a gravitatii normale la nivelul terenului.
In aceasta ipoteza gravitatea normala la nivelul terenului se determina cu relatia:
(2.75)
unde
turtirea elipsoidului (geometrica); (2.76)
turtirea gravimetrica. (2.77)
La lucrarile practice se vor folosi: a=6378137,000mm; f=1:298,3; m=0,003449786
Cu 
s-a notat o
valoare aproximativa pentru altitudine, exprimata in metri.
In numeroase cazuri este suficienta si aproximatia:
Se noteaza si celebra legatura dintre turtirea geometrica si turtirea gravimetrica (teorema Clairaut, 1738):
m. (2.79)
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 5758
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
