Masurarea puterii in retele

Masurarea puterii in retele

Acest capitol este destinat (1) prezentarii diferitelor modalitati de masurare a puterii pe care un actor x, o detine in cadrul unei retele, si a (2) conditiile care influenteaza puterea detinuta.

Potrivit lui Karen S. Cook,[1] exista doua categorii de indicatori de masurare a puterii in cadrul unei retele (R). Este vorba despre indicatori structurali de masurare si indicatorii relationali de masurare. In cele ce urmeaza imi propun sa discut validitatea si capacitatea de masurare a fiecarei categorii de indicatori de masurare a puterii, nu inainte de a face cateva precizari de ordin conceptual cu privire la reteaua de schimb (Rsch).

Rsch trebuie gandita in relatie un urmatorul set de constante conceptuale:

a) Un set de actori (indivizii, grupurile etc. care participa in relatiile de schimb);

b) O distributie de resurse valorizate intre actori;

c) Pentru fiecare actor exista un set de oportunitati de schimb cu alti actori in R;

d) Relatii de schimb - subset al oportunitatilor de schimb. Membrii unei relatii de schimb se presupune ca au un anumit grad de angajament fata de relatie.

Conexiunile si tipuri de conexiuni

Prin Rsch intelegem structura sociala specifica formata din relatii de schimb stabilite intre actori conectati. Un concept esential in cadrul TSR este reprezentat de conexiune.

Cook identifica si defineste doua tipuri de conexiuni, conexiunile pozitive si conexiunile negative. CONEXIUNEA POZITIVA apare atunci cand schimbul de resurse valorizate dintr-o relatie de schimb este influentat de schimbul de resurse care are loc in cealalta relatie.

Spre exemplu, schimbul in relatia A-B, se realizeaza doar in situatia in care se realizeaza schimbul in relatia A-C. Intr-o astfel de situatie, putem vorbi despre o Rsch minimala B-A-C conectata pozitiv. Sau, cu alte cuvinte, in Rsch B-A-C, exista conexiune pozitiva pentru A, daca A beneficiaza de pe urma relatiei de schimb cu B, atata timp cat isi pastreaza relatia de schimb cu C. O astfel de conexiune mai este denumita in limbaj economic drept conexiune "complementara": schimbul de resurse al lui A cu B, creste cererea lui A de schimb de resurse cu C.

CONEXIUNEA NEGATIVA exista daca schimbul dintr-o relatie genereaza lipsa schimbului in alta relatie. Cu alte cuvinte, in Rsch B-A-C exista o conexiune negativa pentru A, daca resursele disponibile de la B si C sunt substituibile reciproc (deci, B si C sunt parteneri de schimb alternativi ai lui A). O astfel de conexiune este definita in limbajul economic drept conexiune "aproape" substituibila ("closely substitutable"), adica schimbul de resurse pe care A il realizeaza cu B, scade cererea lui A de resurse de la C. Cererea de bunuri valorizate implica faptul ca alegerea lui A dintre B si C depinde de: 1. interesul relativ al lui A fata de B si C (valoarea bunului), 2. costul relativ al lui A in achizitia aceleiasi cantitati de bun. Tendinta lui A de a alege intre B si C, alternativa pe baza raportului interes relativ / cost relativ scade pe masura ce gradul de substitutie a bunurilor oferite de B si C creste.

Indiferent daca discutam de conexiuni pozitive sau negative, trebuie subliniat faptul ca orice conexiune variaza in intensitate. Faptul ca doua relatii de schimb, A-B si A-C, au un membru comun, A, nu implica in mod necesar faptul ca B-A-C ar forma o retea minimala si ca cele doua legaturi ar fi conectate, intr-o retea de trei actori. Pentru o Rsch, calitatea de membru nu este suficienta ca principiu de conectare. Pentru a putea discuta de retele de schimb, trebuie sa avem in vedere existenta conexiunilor pozitive, negative sau mixte intre diferitele legaturi diadice existente. In AR, distinctia dintre conexiunile pozitive si conexiunile negative este foarte importanta deoarece tipul de conexiune este produs de conditii sociale.

Walker, Thye si Simpson (2000) dezvolta o alta tipologie a conexiunilor de retea, considerand ca poate fi vorba despre trei tipuri de conexiuni primare si doua secundare.

Primul tip de conexiune primara este denumit drept CONEXIUNE EXCLUSIVA. Astfel, intr-o retea A-B-C, se poate spune ca reteaua este exclusiv conectata la B, daca B-A sau B-C, dar NU B-A si B-C; aceasta retea reprezentand o structura de putere "tare" (unde N > M >= Q = 1).

Pentru o retea A-B-C-D exclusiv conectata la nodurile B si C, resursele castigate de B sunt inferioare celor castigate de B in prima retea (A-B-C); aceasta fiind o structura de putere "slaba". O retea de tipul A-B-C-D, poate fi o retea exclusiv conectata la B si C, cu structura de putere "egala", daca resursele castigate de B sunt egale cu resursele castigate de C.

Al doilea tip de conexiune primara este CONEXIUNEA INCLUSIVA. A-B-C este o retea conectata inclusiv, daca pozitiile din R sunt nevoite sa indeplineasca doua sau mai multe schimburi, pentru a castiga beneficii. A-B-C este o retea conectata inclusiv la B, daca B trebuie sa schimbe si cu A si cu C pentru a obtine beneficii.

Al treilea tip de conexiune primara este CONEXIUNEA NULA. A-B-C este o retea conectata nul la B, daca B poate schimba si castiga beneficii de pe urma unuia sau ambilor parteneri. Adica, N=M>Q=1.

Primul tip de conexiune secundara este CONEXIUNEA INCLUSIV-EXCLUSIVA. B este conectat inclusiv-exclusiv, daca trebuie sa schimbe cu un Ai dintr-un set de A si cu un Ci dintr-un set de C. Adica, N>M>=Q>1. B nu este dezavantajat intr-o conexiune inclusiv-exclusiva, deoarece conexiunea exclusiva elimina efectele conexiunii inclusive.

Al doilea tip de conexiune secundara este CONEXIUNEA INCLUSIV-NULA. B isi transforma reteaua de conexiuni intr-una inclusiv - nula, daca isi sporeste numarul de categorii de noduri cu care sa faca legaturile (face legaturi de schimb cu mai multi Ai si cu mai multi Ci).

Conceptul de pozitie in Rsch

TSR si AR prelucreaza si analizeaza diferitele seturi de date folosind graph-uri (in cazul retelelor cu un numar mic de noduri) si matrici (in cazul retelelor mari, cu un numar mare de noduri ce nu permite reprezentarea acestora in graph-uri).

Intr-un graph, spre exemplu, punctele reprezinta atat actori individuali, cat si actori agregati. Liniile reprezinta relatii de schimb care se stabilesc intre diferite noduri. POZITIA intr-un graph sau intr-o retea este un set de unul sau mai multe puncte / noduri echivalente structural (care ocupa locatii similare din puncte de vedere structural), al carui graph rezidual este isomorfic (prin graph rezidual intelegandu-se graph-ul sau matricea obtinuta prin indepartarea unui anumit punct / nod din graph-ul parental (initial)).

Conceptul de pozitie este extrem de util deoarece simplifica analiza unor Rsch mai complexe. Despre conceptul de pozitie in literatura de specialitate se spune ca este un determinant important al comportamentelor in Rsch.

Oportunitati si relatii de schimb

Intre structurile de oportunitati de schimb si setul de relatii de schimb exista o diferentiere importanta. Structura de oportunitati de schimb ale unui nod (pozitie) reprezinta numarul maxim de relatii de schimb in care nodul respectiv poate intra. Setul de relatii de schimb este un sub-set al structurii de oportunitati de schimb si reprezinta numarul de relatii in care un nod a intrat si pe care le-a ales din structura de oportunitati de schimb. In cele ce urmeaza, voi prezenta diferite forme de retele de schimb, in care sunt puse in evidenta structurile de oportunitati de schimb si seturile de relatii de schimb ale diferitelor noduri (unde liniile solide sunt de 3 ori mai profitabile decat liniile intrerupte).

Relatiile de schimb conectate apar din "oportunitatile de schimb". Conexiunile care apar sunt negative, in cazul de fata. Daca un actor are 2 linii solide (oportunitati de schimb), cei 2 parteneri din cele doua conexiuni sunt pefect intersanjabili ca surse de beneficii.

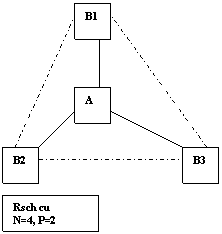R1. Reteaua de 4 persoane si 2 pozitii

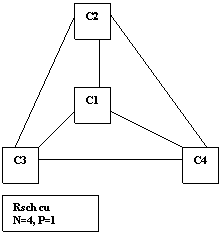
R2. Reteaua de 4 persoane si 1 pozitie

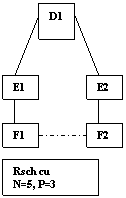
R3. Reteaua de 5 persoane si 3 pozitii

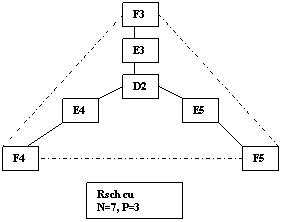
R4. Reteaua de 7 persoane si 3 pozitii

R5. Reteaua de 10 persoane si 3 pozitii

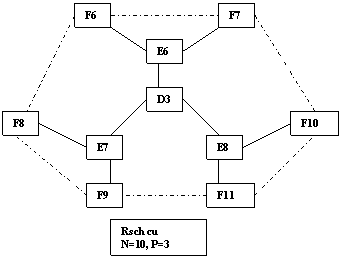
R6. Reteaua de 13 persoane si 3 pozitii

Distributia de putere in retelele de schimb cu conexiuni negative si pozitive

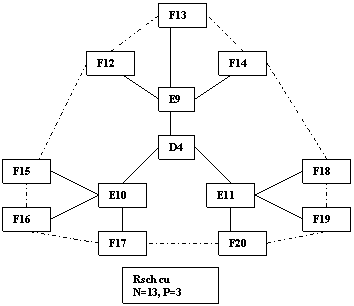
Distributia de putere poate fi studiata ca o functie a pozitiei intr-o structura de oportunitate. Daca cantitatea de resurse tranzactionata, in orice tranzactie, este determinata de negociere, astfel incat beneficiul reciproc este inegal, utilizarea puterii poate fi masurata in termeni de beneficii obtinute prin negociere.

Centralitate si putere in relatiile de schimb conectate negativ Puterea este o functie a pozitiei in R, chiar si atunci cand ocupantii pozitiilor ignora structura de fapt a R si propria pozitie pe care o ocupa in aceasta structura.

Sa luam spre exemplu, R1 si R2. In R1 puterea se concentreaza in pozitia A (cea mai centrala pozitie) si este relativ absenta in pozitiile de periferie B1, B2 si B3. Adica, A este mai putin dependent decat Bx (oricare dintre B1, B2 sau B3). In R2, puterea este distribuita egal intre pozitiile C1, C2, C3 si C4. Reteaua C1-C2-C3-C4 este o retea de putere echilibrata, C1, C2,C3 si C4 fiind egal dependenti.

Pentru a se putea determina pozitia care concentraza cea mai mare putere s-au utilizat in exemplul de mai sus doua criterii: a) gradul de dependenta a unei pozitii X in raport cu celelalte si b) centralitatea fiecarei pozitii in Rsch. Aplicarea fiecarui criteriu in cele doua Rsch R1 si R2 a generat acelasi rezultat. Problema estimarilor cu privire la identificarea pozitiilor care concentraza indici de putere cu valori mari poate fi definita in urmatorii termeni: aplicarea notiunilor teoriei puterii dependenta si a celor bazate doar pe centralitatea structurala genereaza aceleasi rezultate si in retele conectate negativ?Adica, cu alte cuvinte, indicatorii structurali de masurare a puterii (spre exemplu, centralitatea), estimeaza corect modul in care se concentreaza puterea in Rsch conectate negativ, sau este nevoie de alti indicatori de masurare a puterii, cum ar fi indicatorii procesuali de masurare a puterii, de tipul "vulnerabilitatii Rsch in pozitia x"?

Indicatorii structurali de masurare a puterii in Rsch. Punctul de centralitate

Centralitatea structurala este o proprietate a Rsch, care cauta sa testeze existenta unei legaturi intre punctul de centralitate al unei Rsch si locatia de concentrare a puterii in Rsch. Freeman[3] propune trei indicatori de masurare a punctului de centralitate al unei Rsch.

a) indicatorul de masurare a punctului de centralitate bazat pe grade (numarul de legaturi pe care un punct x dintr-o Rsch le are). Punctul slab al acestui indicator ar consta in faptul ca ia in considerare numai legaturile directe, ignorand legaturile indirecte sau efectele indirecte. De asemenea, acest indicator nu ia in calcul intreaga structura a Rsch, fapt cel il face inadecvat pentru masurarea puterii in R.

b) indicatorul de masurare a punctului de centralitate "betweeness" (frecventa cu care un punct cade intre perechi de alte puncte, pe calea cea mai scurta, conectandu-le - este de fapt vorba despre distanta geodezica in R). Acest indicator mai masoara si controlul potential, deoarece identifica punctul care are o localizare strategica, dat fiind faptul ca leaga perechi de puncte (acest indicator a fost utilizat in retelele de comunicare pentru ca determina punctul care avand o asezare strategica, poate distorsiona sau intrerupe comunicarea).

c) Indicatorul de masurare a punctului de centralitate bazat pe apropiere ("closeness") furnizeaza un index al gradului de apropiere al fiecarui punct dintr-o R, de toate celelalte. In acest caz, punctul de centralitate este punctul care are cel mai mic scor in calcularea distantei de la acesta la toate celelalte.

Avantajul ultimilor doi indicatori ai punctului de centralitate in comparatie cu primul indicator consta in faptul ca acestia iau in calcul intreaga structura a Rsch, centrandu-se pe caracteristicile legaturilor sau pe distantele geodezice care leaga toate punctele din retea sau dintr-un graph care descrie o retea.

Exista doua abordari concurente care isi propun sa faca estimari cu privire identificarea puterii in cadrul unei Rsch: abordarea structurala si abordarea puterii dependenta. Prima abordare (a), cea structurala, ai carei indicatori tocmai i-am prezentat, pot fi aplicati pe retele mari, complexe si pot lua in calculul punctului de centralitate intreaga structura de retea. A doua abordare (b), cea relationala (identificabila prin teoria puterii dependenta), este aplicabila la nivelul micro-retelelor si opereaza cu relatii diadice. In acest context, desi aparent pentru nivelul macro-retelelor ar fi indicat calculul indicatorilor structurali de masurare a puterii, la nivelul cercetarilor empirice realizate si prezentate in articolele stiintifice pe care le-am consultat, s-a dovedit ca estimarile realizate prin calculul indicatorilor structurali de masurare a centralitatii nu sunt foarte precise. Mai mult decat atat, acesti indicatori structurali de masurare intalnesc serioase probleme in cazul retelelor de schimb cu conexiuni negative.

Concluzia analizelor realizate la nivelul diferitelor categorii de indicatori de masurare a puterii in Rsch ar fi aceea ca estimarile facute de indicatorii relationali de masurare a puterii sunt mult mai probabile decat cele facute de indicatorii structurali, cel putin pentru Rsch cu conexiuni negative. Asadar, Marsen si Laumann[5], spre exemplu, au ajuns la ideea ca indicatorii de masurare a punctului de centralitate in Rsch cu conexiuni negative, nu fac predictii sau fac predictii slabe, ceea ce arata ca fie centralitatea nu este legata de putere, fie masuratorile sunt limitate numai la un anumit tip de retele. Richard M. Emerson (1983) demonstreaza caracterul limitat al indicatorilor structurali de masurare a puterii in Rsch, pornind de la reteaua de schimb conectata negativ R3.

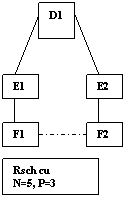
Daca vom calcula punctul de centralitate pentru Rsch 3, prin "betweeness" si "closeness", vom descoperi urmatoarea relatie: D>Ei>Fi. Aceasta relatie ne spune ca persoanele de la centrul R, de care actorii mai periferici sunt dependenti, sunt cei mai puternici din sistem. Adica, in Rsch3, D este punctul cel mai puternic.

Investigand Rsch3, din perspectiva abordarii relationale, vom descoperi ca punctul / pozitia D nu este cea mai importanta, intr-o Rsch cu conexiune negativa.

Putere si dependenta

Dupa cum precizam mai sus, abordarea relationala a puterii in Rsch ofera predictii mult mai puternice decat cele oferite de indicatorii abordarii structurale, desi aceasta se centreaza doar la un nivel de analiza diadic, ce nu integreaza intreaga structura a retelei.

Aducand in discutie abordarea relationala, consider ca se impun a fi facute o serie de referiri la teoria puterii dependenta si la conceptul de dependenta (aceasta teorie apartinand abordarii relationale). Exista doua definiri propuse in acest context de catre Richard M. Emerson (1983):

Din perspectiva celor doua definitii, Richard M. Emerson, lanseaza spre discutie doua ipoteze construite din perspectiva abordarii relationale a puterii in Rsch si raportate la nivelul Rsch3,4,5,6:

Din perspectiva abordarii relationale a distributiei puterii in Rsch 3,4,5 si 6, ordinea estimata a pozitiilor din punctul de vedere al puterii, la momentul de echilibru, va fi E>D=F. Aceasta estimare, asa cum vedem infirma estimarea facuta pe baza indicatorilor structurali de masurare a puterii, D>E=F.

Emerson explica constructia acestei estimari, plecand de la urmatoarele premise:

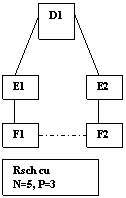Rsch3

Asa cum se poate observa, E1 si E2 au cate un partener de schimb foarte dependent (F1, respectiv, F2) si de la care vor obtine beneficii consistente, daca isi vor folosi puterea rational. Prin folosire rationala a puterii trebuie sa intelegem faptul ca fiecare actor in cadrul Rsch exploreaza sursele alternative de beneficii prin a) extinderea ofertelor catre alte puncte ale Rsch, b) prin compararea ofertelor si contra-ofertelor facute de catre ceilalti. Fiecare actor isi va maximiza beneficiul prin: a) acceptarea celei mai bune oferte din cel putin doua, pe care le are, b) micsorarea ofertei atunci cand contra-ofertele devin inacceptabile, c) asteptarea unei oferte mai bune atunci cand are posibilitatea de a face acest lucru.

Aparenta de egalitate de putere intre pozitiile D si E este de scurta durata. Pentru accesul la E1 si E2, D1 trebuie sa lupte cu F1 si F2 care nu au alta alternativa. Deci, F-E-D este o Rsch cu conexiune negativa, in care ocupantul pozitiei D este la fel de slab ca si actorii periferici F1 si F2, iar ocupantii pozitiei E (E1 si E2), devin din ce in ce mai puternici, pe masura ce relatiile de schimb evolueaza in decursul timpului, ajungand in cele din urma la punctul de echilibru.

Rezulta ca: (1) pozitia in retea determina gradul de disponibilitate al resurselor pentru fiecare pozitie; (2) daca stimulentele ce orienteaza comportamentul punctelor din Rsch catre schimb sunt mari (resursele tranzactionate sunt inalt valorizate) de-alungul Rsch, atunci pozitia va crea diferente in gradele de disponibilitate a resurselor, aceasta determinand dependenta si, deci, putere; (3) daca stimulentele ce orienteaza comportamentul punctelor din Rsch catre schimb sunt scazute uniform, nici un actor din Rsch nu va fi foarte dependent de ceilalti, iar potentialele inegalitati de putere vor fi reduse, atenuate de-alungul R, indiferent de pozitie.

Puterea ca potential, utilizarea puterii si punctul de echilibru in Rsch

Puterea ca potential este definita, din perspectiva teoriei puterii dependenta, ca: potential de a castiga beneficii mai mari, pe cheltuiala altora in relatiile de schimb diadice.

Structura Rsch ajuta la determinarea potentialului de putere pentru fiecare pozitie in Rsch, dar ocupantii acestor pozitii pot folosi puterea in grade si rate variabile. Daca puterea este folosita la limitele sale teoretice, atunci actorul mai putin puternic nu va mai obtine beneficii de la actorul mai puternic. Pentru Rsch3, situatia de echilibru este definita in urmatorul model de distributie a resurselor:

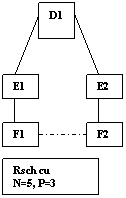
Rsch3 la punctul de echilibru

(daca consideram ca liniile solide indica tranzactionarea

a maxim 24 de unitati valorice, iar liniile intrerupte

maxim 8 unitati valorice, atunci la punctul de echilibru,

in conditiile de folosire rationala a puterii in Rsch,

vom avea urmatoarea negociere de resurse

D1 - E1 4:20, D1 - E2 4:20

E1 - F1 20:4, E2 - F2 20:4

F1 - F2

In Rsch 4,5 si 6, punctul de echilibru in distributia resurselor este identic, chiar daca marimea retelelor variaza, gradul de disponibilitate a resurselor pentru Di si Ej variaza in timp. Ceea ce rezulta ar fi ca gradul de disponibilitate a resurselor din surse alternative determina dependenta pozitionala relativa si ca dependenta pozitionala relativa de-alungul Rsch conectate negativ determina gradul de putere al ocupantilor fiecarei pozitii. Desi pozitiile D si E au un numar egal de surse alternative, gradul de disponibilitate relativa a resurselor pentru D de la E se atenueaza o data cu trecerea timpului, functie a dependentei pozitiei F de E. Marsden considera ca numarul de alternative impreuna cu valoarea resurselor tranzactionate sunt principalii determinanti ai dependentei.

Trebuie sa fac in acest context precizarea ca gradul de disponibilitate al resurselor pentru un actor X nu este acelasi lucru cu numarul de alternative pe care actorul X le are. Acest lucru poate fi redefinit in forma; nu conteaza cate alternative proste de furnizare a resurselor are o pozitie, ci gradul de disponibilitate a resurselor respective. Concret, in Rsch3, atat pozitia D, cat si pozitia E au acelasi numar de alternative, insa grade de disponibilitate a resurselor diferite.

Dependenta si vulnerabilitatea de retea

Asa cum am precizat mai sus, abordarea puterii prin indicatori structurali de masurare a punctului de centralitate al unei Rsch, desi ia in calcul intraga structura a Rsch, specificand gradul de centralitate al fiecarei pozitii din retea, nu reuseste sa sustina puternic legatura dintre centralitate si putere. Din acest motiv, abordarea relationala a puterii in Rsch, propune un indicator de masurare a puterii in Rsch mult mai puternic. Acest indicator este definit drept vulnerabilitatea unei Rsch X in punctul y. Acest indicator masoara de fapt volumul de pierderi pe care Rsch le suporta prin indepartarea unui punct x din Rsch. Pentru a calcula indicatorul de vulnerabilitate, se construieste un graph rezidual pe baza graph-ului initial. Graph-ul rezidual se obtine indepartand punctul x din graph-ul initial. Prin "indepartare" se defineste orice forma de retragere din relatia de schimb a punctului x. Comparand graph-ul initial (G) cu graph-ul rezidual GRx, se poate constata daca structura GRx este slabita in ceea ce priveste fluxul de resurse tranzactionate. Definind pozitia ca un set de puncte de Rsch ale caror GR sunt izomorfice, este nevoie sa existe doar atatea G - GRx comparatii cate pozitii sunt in structura Rsch (GR pentru puncte care ocupa aceeasi pozitie in Rsch sunt identice). Ceea ce se poate calcula dupa indepartarea unui punct din graph este reductia din fluxul maxim (RFM). Iata cum ar arata procedeul de calcul al RFM, deci a indicatorului de vulnerabilitate al Rsch X in punctul y, pentru Rsch3:

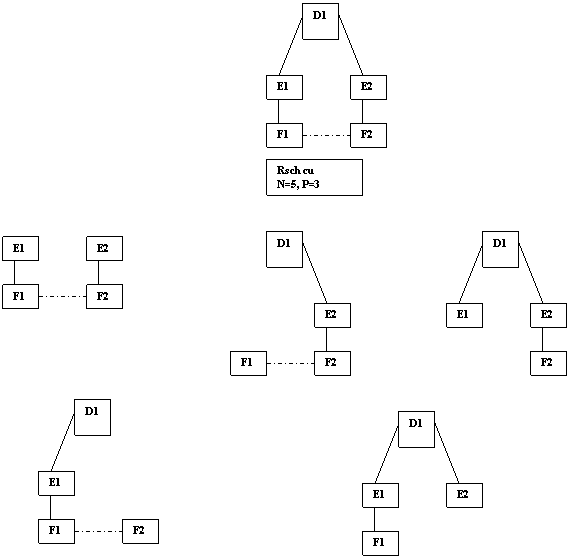
Graful initial al Rsch 3 se regaseste in

forma din partea dreapta

Grafurile reziduale pentru fiecare punct al Rsch 3 arata in felul urmator:

GR(D1) - pentru punctul D1

GR(E1) GR (F1)

GR (E2) GR (F2)

Dupa indepartarea succesiva a punctelor din Rsch3, trecem la compararea G cu GR obtinute:

Asa cum se poate constata din tabelul comparativ de mai sus, Rsch3 este vulnerabila in punctele E1 si E2 sau, altfel spus, in pozitia E. Daca Rsch 3 ar fi lipsita de una dintre pozitiile F sau D, rata de flux maxim nu ar suferi pierderi. Daca insa Rsch 3 ar fi lipsita de pozitia E, reductia de flux maxim ar fi de 16; deci Rsch 3 ar suferi pierderi importante. Calculand RFM, descoperim, deci, ca Rsch3 este vulnerabila in punctele E1 si E2.

Prin calcularea RFM, am descoperit ca dependenta minima este localizata la nivelul punctelor E1 si E2, deci in pozitia E. De asemenea, am masurat dependenta intregii retele Rsch3 de fiecare din punctele sale. Ceea ce se poate observa ar fi faptul ca Rsch 3 este vuilnerabila sau dependenta doar de pozitia E.

Dependenta si centralitatea la nivel de retea

In retelele de schimb conectate negativ, am observat ca indicatorii structurali de masurare a puterii sunt limitati in a oferi predictii "tari". In al doilea rand, am observat ca "vulnerabilitatea unei retele de schimb x intr-un punct y" este un indicator destul de eficient in masurarea puterii si in analizarea distributiei puterii, pentru Rsch sensibile la tipul de conexiune existent intre relatiile de schimb.

Rsch3, cu conexiuni pozitive

Daca Rsch3 ar fi fost o retea de schimb conectata pozitiv la E (adica E1- F1 este dependenta de E1-D), atunci "indepartarea" lui D din Rsch3, ar fi redus considerabil capacitatea retelei de a schimba resurse si, deci, Rsch3 ar fi fost vulnerabila in punctul D1. Astfel, pentru ca E sa continue sa primeasca "resurse valorizate" de la F, in Rsch3, E ar fi devenit dependent de D, pentru a mentine fluxul resurselor la pozitia E. Deci, fluxul de resurse in Rsch3 ar fi inalt dependent de pozitia D, reorientand puterea la "centru", intr-o Rsch3 cu conexiuni pozitive. Intr-o astfel de situatie, indicatorul structural de masurare a "punctului de centralitate" ar fi consistent in valorile si predictiile generate cu indicatorul vulnerabilitatii unei retele de schimb la un punct din retea.

Consideratii finale cu privire la abordarile concurente structurala si relationala

Din analiza modului in care puterea se distribuie intr-o Rsch cu conexiuni negative, se poate formula "principiul descentralizarii": Rsch cu conexiuni negative tind sa determine sisteme de schimb organizate in jurul unor nuclee de putere multipli concentrati in punctele Ej (in pozitia E).

Punctele definite ca "centrale" (prin indicatorii structurali de masurare a "punctelor de centralitate") nu sunt identice cu punctele "centrale" definite prin reductia de flux maxim (indicatorul de vulnerabilitate a Rsch x in punctul y). Acest lucru ne arata faptul ca indicatorii structurali de masurare a puterii nu pot opera eficient in Rsch conectate negativ.

Spre deosebire de limitele pe care le au indicatorii structurali de masurare a puterii in Rsch, RFM (reductia de flux maxim ca masura a "vulnerabilitatii Rsch x in punctul y") poate fi aplicat si in retele de schimb cu conexiune pozitiva. In astfel de situatii, rezultatele generate de RFM corespund rezultatelor generate de indicatorul structural de masurare a punctului de centralitate "betweeness".

Alti indicatori de maurare a puterii in Rsch

Intr-o relatie de schimb de tip diadic, puterea lui A asupra lui B (PAB) este egala cu dependenta lui B fata de A (DBA), unde DBA creste o data cu cresterea interesului lui B fata de resursa oferita de A si scade o data cu cresterea numarului de resurse alternative de a obtine resursa lui A, pe care B le are[9].

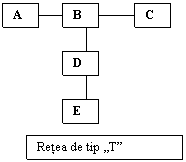
Indicatorul structural de masurare a puterii GPI Markovsky, Willer si Patton[10] pentru a aborda puterea structurala, au dezvoltat graph-ul indexului de putere teoretica (GPI). Acest GPI este suma numarului de legaturi care nu se intersecteaza de marime variabila, unde legaturile de marime impara sunt masurate prin (+1), iar cele de marime para sunt masurate prin (-1). De la nodul A, in reteaua de tip "T", porneste o legatura de marime 1 (A-B), o legatura care nu intersecteaza de marime 2 (A-B-C sau A-B-D, care au comun/isi impart marginea A-B) si o legatura de marime 3 (A-B-D-E). Din acestea rezulta ca puterea lui A (sau a lui C) este egala cu 1-1+1=1. Puterea lui B este egala cu 3-1=2. D are doua legaturi de marime 1 (D-E si D-B) si o legatura de marimea 2 (D-B-A sau D-B-C, care au comun/isi impart marginea D-B). Deci, puterea lui D este 2-1=1. GPI-ul lui E este 1-1+1=1. Deci, potrivit GPI, B are cea mai puternica pozitie in cadrul retelei.

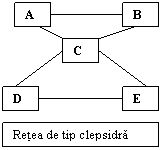
Indicatorul structural de masurare a "puterii slabe" Markovsky, Skvoretz, Willer, Lovaglia si Erger[11] propun un nou model pentru "puterea slaba" (weak power) in retea (probabilitatile de putere slaba). Intr-o retea de tip "clepsidra", sa presupunem ca toti partenerii de schimb sunt completi, adica daca doi actori au intrat intr-o relatie de schimb, acestia nu mai sunt disponibili pentru a intra in alte relatii de schimb. Exista cinci modele (AB/CD, AB/CE, AC/DE, BC/DE, AB/DE), si fiecare dintre aceste modele exclude o pozitie. In final, drept urmare, reteaua de tip clepsidra ar trebui sa evidentieze diferente de putere slaba. Diferentele de putere care pot fi estimate in retele de putere slaba se bazeaza pe calculul probabilitatii de incluziune: cu cat probabilitatea de incluziune intr-o relatie de schimb este mai mare, cu atat puterea este mai mare. Probabilitatile de incluziune se bazeaza pe asumptia ca nodurile se aleg intamplator in relatia de schimb si ca o relatie de schimb este completa daca doua noduri se aleg intamplator. Astfel, in reteaua clepsidra, de exemplu, s-a calculat probabilitatea de incluziune pentru C (0,8205) si probabilitatea de incluziune pentru celelalte noduri (0,7949). Concluzia este ca C ar trebui sa aiba cea mai mare putere in relatiile sale de schimb.

Determinantii puterii in retelele de schimb

Kazuo Yamagushi[12] considera ca setul de constrangeri ale retelei care actioneaza asupra schimbului fac ca puterea unui actor sa depinda in parte de pozitia ocupata in retea. Puterea este o caracteristica a relatiilor de schimb si nu o proprietate a fiecarui actor individual. Interdependenta dintre relatiile de schimb ale fiecarui actor cu partenerii sai, genereaza situatii in care puterea emerge ca un rezultat al schimburilor rationale facute de actori cu partenerii sai.

Spre deosebire de profesorul japonez al Univeristatii din Chicago, James Coleman considera ca puterea este o proprietate a actorului dat fiind faptul ca valoarea resurselor si, in consecinta, puterea actorilor care controleaza resursele nu se schimba, cand actorii tranzactioneaza resurse pentru maximizarea utilitatii. Coleman sustine ca actiunea fiecarui actor de maximizare a utilitatii afecteaza puterea partenerilor. Schimbarea care are loc drept consecinta in distributia puterii face necesar ca toti actorii sa-si ajusteze actiunile de maximizare a utilitatii. Acest lucru genereaza un punct de echilibru, in care puterea actorilor, cat si actiunile lor de maximizare a utilitatii nu se mai schimba. Ajustarile catre actiuni ce maximizeaza utilitatea determina o stare de echilibru in Rsch.

Asadar, puterea este o proprietate atat de relatie, cat si de structura a schimbului si indica valoarea totala a tuturor resurselor controlate de fiecare actor intr-un punct de echilibru.

Yamagushi admite totusi faptul ca trebuie sa se faca o diferentiere teoretica intre determinantii structurali si cei relationali ai puterii in Rsch. Facand referire la conexiunile pozitive si negative ale unei Rsch, acesta considera ca trebuie sa se tina cont, pe de o parte, de structura de retea a schimbului (daca A are relatii de schimb cu B sau C), si, pe de cealalta parte, de relatiile de schimb interdependente (daca relatiile de schimb ale lui A cu B si C sunt "aproape substituibile", "complementare" sau independente. Deci, indicatorii de masurare a puterii trebuie sa tina cont, atat de cauzele structurale ale exploatabilitatii (cum ar fi dependenta de cativa actori), cat si de cauza relationala a exploatabilitatii (gradul inalt de substitutabilitate a relatiilor de schimb).

In concluzie, trebuie retinut faptul ca o masurare cat mai buna a puterii in Rsch trebuie sa tina cont atat de factorii structurali, cat si de cei relationali. Asa cum am vazut mai sus, puterea in Rsch trebuie sa fie masurata prin indicatori de natura mixta (structurali si relationali), in caz contrar, predictiile obtinute fiind foarte slabe (a se vedea limita indicatorilor structurali de a estima puterea in Rsch cu conexiune negativa).