| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The properties of matrix addition and multiplication depend on the properties of the underlying number system. In this section, we define three different kinds of underlying number systems: quasirings, rings, and fields. We can define matrix multiplication over quasirings, and Strassen s matrix-multiplication algorithm works over rings. We then present a simple trick for reducing boolean matrix multiplication, which is defined over a quasiring that is not a ring, to multiplication over a ring. Finally, we discuss why the properties of a field cannot naturally be exploited to provide better algorithms for matrix multiplication.
Let ![]() denote a number
system, where S is a set of elements,
denote a number
system, where S is a set of elements, ![]() and
and ![]() are binary
operations on S (the addition and multiplication operations,
respectively), and
are binary
operations on S (the addition and multiplication operations,
respectively), and ![]() are distinct
distinguished elements of S. This system is a quasiring if
it satisfies the following properties:
are distinct
distinguished elements of S. This system is a quasiring if
it satisfies the following properties:
1. ![]() is a monoid:
is a monoid:
![]() S is closed
under
S is closed
under ![]() ; that is, a
; that is, a
![]() b
b ![]() S for all
a, b
S for all
a, b ![]() S.
S.
![]()
![]() is associative;
that is, a
is associative;
that is, a ![]() (b
(b ![]() c) = (a
c) = (a
![]() b)
b) ![]() c for all
a, b, c
c for all
a, b, c ![]() S.
S.
![]()
![]() is an identity
for
is an identity
for ![]() ; that is,
; that is, ![]() for all a
for all a
![]() S.
S.
Likewise, ![]() is a monoid.
is a monoid.
2. ![]() is an annihilator,
that is,
is an annihilator,
that is, ![]() for all a
for all a
![]() S.
S.
3. The operator ![]() is commutative;
that is, a
is commutative;
that is, a ![]() b = b
b = b ![]() a for all
a, b
a for all
a, b ![]() S.
S.
4. The operator ![]() distributes
over
distributes
over ![]() ; that is,
; that is, ![]() and
and ![]() for all a,b,c
for all a,b,c
![]() S.
S.
Examples of quasirings include the
boolean quasiring (, ![]()
![]() , 0, 1), where
, 0, 1), where ![]() denotes logical OR and
denotes logical OR and ![]() denotes logical AND, and the natural number system (N, +,
denotes logical AND, and the natural number system (N, +, ![]() , 0, 1), where +
and
, 0, 1), where +
and ![]() denote ordinary
addition and multiplication. Any closed semiring (see Section 26.4) is also a
quasiring; closed semirings obey additional idempotence and infinite-sum
properties.
denote ordinary
addition and multiplication. Any closed semiring (see Section 26.4) is also a
quasiring; closed semirings obey additional idempotence and infinite-sum
properties.
We can extend ![]() and
and ![]() to matrices as
we did for + and
to matrices as
we did for + and ![]() in Section 1.
Denoting the n
in Section 1.
Denoting the n ![]() n
identity matrix composed of
n
identity matrix composed of ![]() we find that
matrix multiplication is well defined and the matrix system is itself a
quasiring, as the following theorem states.
we find that
matrix multiplication is well defined and the matrix system is itself a
quasiring, as the following theorem states.
Theorem 7
If ![]() is a quasiring
and n
is a quasiring
and n ![]() 1, then
1, then ![]() is a quasiring.
is a quasiring.
Proof The proof is left as Exercise 3-3.
Subtraction is not defined for quasirings, but it is
for a ring, which is a quasiring ![]() that satisfies
the following additional property:
that satisfies
the following additional property:
5. Every element in S has
an additive inverse; that is, for all a ![]() S, there
exists an element b
S, there
exists an element b ![]() S such
that
S such
that ![]() . Such a b
is also called the negative of a and is denoted (-a).
. Such a b
is also called the negative of a and is denoted (-a).
Given that the negative of any element is defined, we can define subtraction by a - b = a + (-b).
There are many examples
of rings. The integers (Z, +, ![]() , 0, 1) under
the usual operations of addition and multiplication form a ring. The integers
modulo n for any integer n > 1 that is, (Zn,
+,
, 0, 1) under
the usual operations of addition and multiplication form a ring. The integers
modulo n for any integer n > 1 that is, (Zn,
+, ![]() , 0, 1), where +
is addition modulo n and
, 0, 1), where +
is addition modulo n and ![]() is
multiplication modulo n--form a ring. Another example is the set R[x]
of finite-degree polynomials in x with real coefficients under the usual
operations--that is, (R[x], +,
is
multiplication modulo n--form a ring. Another example is the set R[x]
of finite-degree polynomials in x with real coefficients under the usual
operations--that is, (R[x], +, ![]() , 0, 1), where +
is polynomial addition and
, 0, 1), where +
is polynomial addition and ![]() is polynomial
multiplication.
is polynomial
multiplication.
The following corollary shows that Theorem 7 generalizes naturally to rings.
Corollary 8
If ![]() is a ring and n
is a ring and n
![]() 1, then
1, then ![]() is a ring.
is a ring.
Proof The proof is left as Exercise 3-3.
Using this corollary, we can prove the following theorem.
Theorem 9
Strassen's matrix-multiplication algorithm works properly over any ring of matrix elements.
Proof Strassen's algorithm depends on the correctness of the algorithm for 2 ![]() 2 matrices,
which requires only that the matrix elements belong to a ring. Since the matrix
elements do belong to a ring, Corollary 8 implies the matrices themselves form
a ring. Thus, by induction, Strassen's algorithm works correctly at each level
of recursion.
2 matrices,
which requires only that the matrix elements belong to a ring. Since the matrix
elements do belong to a ring, Corollary 8 implies the matrices themselves form
a ring. Thus, by induction, Strassen's algorithm works correctly at each level
of recursion.
Strassen's algorithm for matrix multiplication, in fact, depends critically on the existence of additive inverses. Out of the seven products P1, P2, . . . ,P7, four involve differences of submatrices. Thus, Strassen's algorithm does not work in general for quasirings.
Strassen's algorithm cannot be
used directly to multiply boolean matrices, since the boolean quasiring (,
![]()
![]() , 0, 1) is not a ring. There are instances in which a quasiring is
contained in a larger system that is a ring. For example, the natural numbers
(a quasiring) are a subset of the integers (a ring), and Strassen's algorithm
can therefore be used to multiply matrices of natural numbers if we consider
the underlying number system to be the integers. Unfortunately, the boolean
quasiring cannot be extended in a similar way to a ring. (See Exercise 3-4.)
, 0, 1) is not a ring. There are instances in which a quasiring is
contained in a larger system that is a ring. For example, the natural numbers
(a quasiring) are a subset of the integers (a ring), and Strassen's algorithm
can therefore be used to multiply matrices of natural numbers if we consider
the underlying number system to be the integers. Unfortunately, the boolean
quasiring cannot be extended in a similar way to a ring. (See Exercise 3-4.)
The following theorem presents a simple trick for reducing boolean matrix multiplication to multiplication over a ring. Problem 31-1 presents another efficient approach.
Theorem 10
If M(n)
denotes the number of arithmetic operations required to multiply two n ![]() n
matrices over the integers, then two n
n
matrices over the integers, then two n ![]() n boolean matrices can be multiplied using O(M(n))
arithmetic operations.
n boolean matrices can be multiplied using O(M(n))
arithmetic operations.
Proof Let the two matrices be A and B, and let C = AB in the boolean quasiring, that is,
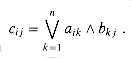
Instead of computing over the boolean quasiring, we compute the product C' over the ring of integers with the given matrix-multiplication algorithm that uses M(n) arithmetic operations. We thus have
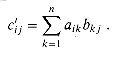
Each term aikbkj
of this sum is 0 if and only if aik ![]() bkj = 0, and 1 if and only if aik
bkj = 0, and 1 if and only if aik ![]() bkj = 1. Thus, the integer sum
bkj = 1. Thus, the integer sum ![]() is 0 if and only
if every term is 0 or, equivalently, if and only if the boolean OR of the
terms, which is cij, is 0. Therefore, the boolean matrix C
can be reconstructed with
is 0 if and only
if every term is 0 or, equivalently, if and only if the boolean OR of the
terms, which is cij, is 0. Therefore, the boolean matrix C
can be reconstructed with ![]() (n2)
arithmetic operations from the integer matrix C' by simply comparing
each
(n2)
arithmetic operations from the integer matrix C' by simply comparing
each ![]() with 0. The
number of arithmetic operations for the entire procedure is then O(M(n))
+
with 0. The
number of arithmetic operations for the entire procedure is then O(M(n))
+![]() (n2)
= O(M(n)), since M(n) =
(n2)
= O(M(n)), since M(n) = ![]() (n2).
(n2).
Thus, using Strassen's algorithm, we can perform boolean matrix multiplication in O(n lg 7) time.
The normal method of multiplying boolean matrices uses only boolean variables. If we use this adaptation of Strassen's algorithm, however, the final product matrix can have entries as large as n, thus requiring a computer word to store them rather than a single bit. More worrisome is that the intermediate results, which are integers, may grow even larger. One method for keeping intermediate results from growing too large is to perform all computations modulo n + 1. Exercise 3-5 asks you to show that working modulo n + 1 does not affect the correctness of the algorithm.
A ring ![]() is a field
if it satisfies the following two additional properties:
is a field
if it satisfies the following two additional properties:
6. The operator ![]() is commutative;
that is,
is commutative;
that is, ![]() for all a, b
for all a, b
![]() S.
S.
7. Every nonzero element in S has a multiplicative
inverse; that is, for all ![]() , there exists
an element b
, there exists
an element b ![]() S such
that
S such
that ![]() .
.
Such an element b is often called the inverse of a and is denoted a-1.
Examples of fields
include the real numbers (R, +, ![]() , 0, 1), the
complex numbers (C, +,
, 0, 1), the
complex numbers (C, +, ![]() , 0, 1), and the
integers modulo a prime p: (Zp, +,
, 0, 1), and the
integers modulo a prime p: (Zp, +, ![]() , 0, 1).
, 0, 1).
Because fields offer multiplicative inverses of elements, division is possible. They also offer commutativity. By generalizing from quasirings to rings, Strassen was able to improve the running time of matrix multiplication. Since the underlying elements of matrices are often from a field--the real numbers, for instance--one might hope that by using fields instead of rings in a Strassen-like recursive algorithm, the running time might be further improved.
This approach seems
unlikely to be fruitful. For a recursive divide-and-conquer algorithm based on
fields to work, the matrices at each step of the recursion must form a field.
Unfortunately, the natural extension of Theorem 7 and Corollary 8 to fields
fails badly. For n > 1, the set of n ![]() n
matrices never forms a field, even if the underlying number system is a
field. Multiplication of n
n
matrices never forms a field, even if the underlying number system is a
field. Multiplication of n ![]() n matrices is not commutative, and many n
n matrices is not commutative, and many n
![]() n matrices do not have inverses. Better
algorithms for matrix multiplication are therefore more likely to be based on
ring theory than on field theory.
n matrices do not have inverses. Better
algorithms for matrix multiplication are therefore more likely to be based on
ring theory than on field theory.
Does Strassen's algorithm
work over the number system (Z[x], +, ![]() , 0, 1), where Z[x]
is the set of all polynomials with integer coefficients in the variable x
and + and
, 0, 1), where Z[x]
is the set of all polynomials with integer coefficients in the variable x
and + and ![]() are ordinary
polynomial addition and multiplication?
are ordinary
polynomial addition and multiplication?
Explain why Strassen's
algorithm doesn't work over closed semirings (see Section 26.4) or over the
boolean quasiring (, ![]()
![]()
Prove Theorem 7 and Corollary 8.
Show that the boolean
quasiring (, ![]()
![]() , 0, 1) cannot be embedded in a ring. That is, show that it is
impossible to add a '-1' to the quasiring so that the resulting
algebraic structure is a ring.
, 0, 1) cannot be embedded in a ring. That is, show that it is
impossible to add a '-1' to the quasiring so that the resulting
algebraic structure is a ring.
Argue that if all computations in the algorithm of Theorem 10 are performed modulo n + 1, the algorithm still works correctly.
Show how to determine efficiently if a given undirected input graph contains a triangle (a set of three mutually adjacent vertices).
Show
that computing the product of two n ![]() n boolean
matrices over the boolean quasiring is reducible to computing the transitive
closure of a given directed 3n-vertex input graph.
n boolean
matrices over the boolean quasiring is reducible to computing the transitive
closure of a given directed 3n-vertex input graph.
Show how to compute the transitive closure of a given directed n-vertex input graph in time O(nlg 7 lg n). Compare this result with the performance of the TRANSITIVE CLOSURE procedure in Section 26.2.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2177
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved