Pythagorean theorem

Pythagoras of Samos ( born between 580 and 572 BC, died between 500 and 490 BC) was an Ionian Greek mathematician and founder of the religious movement called Pythagoreanism. Pythagoras was born on Samos, a Greek island in the eastern Aegean, off the coast of Asia Minor. He is often revered as a great mathematician, mystic and scientist; however some have questioned the scope of his contributions to mathematics and natural philosophy. As a young man, he left his native city for Croton, Calabria, in Southern Italy, to escape the tyrannical government of Polycrate. He is best known for the Pythagorean theorem, which bears his name. Know as 'the father of numbers'. He was the first man to call himself a philosopher, or lover of wisdom, and Pythagorean ideas exercised a marked influence on Plato. Unfortunately, very little is known about Pythagoras because none of his writings have survived. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues and successors.

The Pythagorean theorem: The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c). In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship between the sides of a right triangle, knowledge of the relationship between adjacent angles, and proofs of the theorem.

Megalithic monuments from circa 2500 BC in Egypt, and in Northern Europe, incorporate right triangles with integer sides. Bartel Leendert van der Waerden conjectures that these Pythagorean triples were discovered algebraically.

Written between 2000 and 1786 BC, the Middle Kingdom Egyptian papyrus Berlin 6619 includes a problem whose solution is a Pythagorean triple.

During the reign of Hammurabi the Great, the Mesopotamian tablet Plimpton 322, written between 1790 and 1750 BC, contains many entries closely related to Pythagorean triples.

The Baudhayana Sulba Sutra, the dates of which are given variously as between the 8th century BC and the 2nd century BC, in India, contains a list of Pythagorean triples discovered algebraically, a statement of the Pythagorean theorem, and a geometrical proof of the Pythagorean theorem for an isosceles right triangle.

The Apastamba Sulba Sutra (circa 600 BC) contains a numerical proof of the general Pythagorean theorem, using an area computation. Van der Waerden believes that 'it was certainly based on earlier traditions'. According to Albert Bŭrk, this is the original proof of the theorem; he further theorizes that Pythagoras visited Arakonam, India, and copied it.

Pythagoras, whose dates are commonly given as 569475 BC, used algebraic methods to construct Pythagorean triples, according to Proklos's commentary on Euclid. Proklos, however, wrote between 410 and 485 AD. According to Sir Thomas L. Heath, there is no attribution of the theorem to Pythagoras for five centuries after Pythagoras lived. However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.

Around 400 BC, according to Proklos, Plato gave a method for finding Pythagorean triples that combined algebra and geometry. Circa 300 BC, in Euclid's Elements, the oldest extant axiomatic proof of the theorem is presented.

Written sometime between 500 BC and 200 AD, the Chinese text Chou Pei Suan Ching, (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a visual proof of the Pythagorean theorem in China it is called the 'Gougu Theorem' for the (3, 4, 5) triangle. During the Han Dynasty, from 202 BC to 220 AD, Pythagorean triples appear in The Nine Chapters on the Mathematical Art, together with a mention of right triangles

Proof using similar triangles

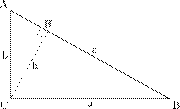
Proof using similar triangles

Like most of the proofs of the Pythagorean theorem, this one is based on the proportionality of the sides of two similar triangles.

Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. We draw the altitude from point C, and call H its intersection with the side AB. The new triangle ACH is similar to our triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well. By a similar reasoning, the triangle CBH is also similar to ABC. The similarities lead to the two ratios. As

so

These can be written as

Summing these two equalities, we obtain

In other words, the Pythagorean theorem:

Algebraic proof

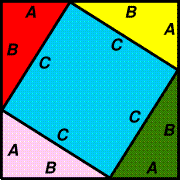
An algebraic variant of this proof is provided by the following reasoning. Looking at the illustration which is a large square with identical right triangles in its corners, the area of each of these four triangles is given by an angle corresponding with the side of length C.

A square created by aligning four right angle triangles and a large square.

The A-side angle and B-side angle of each of these triangles are complementary angles, so each of the angles of the blue area in the middle is a right angle, making this area a square with side length C. The area of this square is C². Thus the area of everything together is given by:

However, as the large square has sides of length A + B, we can also calculate its area as (A + B)², which expands to A² + 2AB + B².

(Distribution of the 4)

(Subtraction of 2AB)

Generalizations

The Pythagorean theorem was generalized by Euclid in his Elements:

If one erects similar figures (see Euclidean geometry) on the sides of a right triangle, then the sum of the areas of the two smaller ones equals the area of the larger one.

The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:

where θ is the angle between sides a and b.

When θ is 90 degrees, then cos(θ) = 0, so the formula reduces to the usual Pythagorean theorem.