| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Finding all occurrences of a pattern in a text is a problem that arises frequently in text-editing programs. Typically, the text is a document being edited, and the pattern searched for is a particular word supplied by the user. Efficient algorithms for this problem can greatly aid the responsiveness of the text-editing program. String-matching algorithms are also used, for example, to search for particular patterns in DNA sequences.
We formalize the string-matching
problem as follows. We assume that the text is an array T[1 . . n]
of length n and that the pattern is an array P[1 . . m] of
length m. We further assume that the elements of P and T
are characters drawn from a finite alphabet ![]() . For
example, we may have
. For
example, we may have ![]() = or
= or ![]() = . The character arrays P
and T are often called strings of characters.
= . The character arrays P
and T are often called strings of characters.
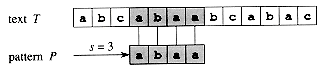
We say that pattern P occurs
with shift s in text T (or, equivalently, that
pattern P occurs beginning at position s + 1 in text T)
if 0 ![]() s
s ![]() n - m
and T[s + 1 . . s + m] = P[1 . . m]
(that is, if T[s + j] = P[j], for 1
n - m
and T[s + 1 . . s + m] = P[1 . . m]
(that is, if T[s + j] = P[j], for 1 ![]() j
j ![]() m).
If P occurs with shift s in T, then we call s a valid
shift; otherwise, we call s an invalid shift. The
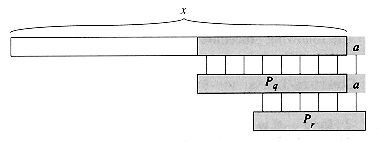
string-matching problem is the problem of finding all valid shifts with which a
given pattern P occurs in a given text T. Figure 1 illustrates
these definitions.
m).
If P occurs with shift s in T, then we call s a valid
shift; otherwise, we call s an invalid shift. The
string-matching problem is the problem of finding all valid shifts with which a
given pattern P occurs in a given text T. Figure 1 illustrates
these definitions.
This chapter is organized
as follows. In Section 1 we review the naive brute-force algorithm for the
string-matching problem, which has worst-case running time O((n -
m + 1)m). Section 2 presents an interesting string-matching
algorithm, due to Rabin and Karp. This algorithm also has worst-case running
time O((n - m + 1)m), but it works much better on
average and in practice. It also generalizes nicely to other pattern-matching
problems. Section 3 then describes a string-matching algorithm that begins by
constructing a finite automaton specifically designed to search for occurrences
of the given pattern P in a text. This algorithm runs in time O(n
+ m ![]()
![]()
![]() ). The
similar but much cleverer Knuth-Morris-Pratt (or KMP) algorithm is presented in
Section 4; the KMP algorithm runs in time O(n + m).
Finally, Section 5 describes an algorithm due to Boyer and Moore that is often
the best practical choice, although its worst-case running time (like that of
the Rabin-Karp algorithm) is no better than that of the naive string-matching
algorithm.
). The
similar but much cleverer Knuth-Morris-Pratt (or KMP) algorithm is presented in
Section 4; the KMP algorithm runs in time O(n + m).
Finally, Section 5 describes an algorithm due to Boyer and Moore that is often
the best practical choice, although its worst-case running time (like that of
the Rabin-Karp algorithm) is no better than that of the naive string-matching
algorithm.
Notation and terminology
We shall let ![]() * (read
'sigma-star') denote the set of all finite-length strings formed
using characters from the alphabet
* (read
'sigma-star') denote the set of all finite-length strings formed
using characters from the alphabet ![]() . In this
chapter, we consider only finite-length strings. The zero-length empty
string, denoted
. In this
chapter, we consider only finite-length strings. The zero-length empty
string, denoted ![]() , also belongs
to
, also belongs
to ![]() *. The
length of a string x is denoted |x|. The concatenation of
two strings x and y, denoted xy, has length |x| + |y|
and consists of the characters from x followed by the characters from y.
*. The
length of a string x is denoted |x|. The concatenation of
two strings x and y, denoted xy, has length |x| + |y|
and consists of the characters from x followed by the characters from y.
We say
that a string w is a prefix of a string x, denoted ![]() for some
string y
for some
string y ![]()
![]() *. Note that
if
*. Note that
if ![]() , then |w|
, then |w|
![]() |x|.
Similarly, we say that a string w is a suffix of a string x,
denoted
|x|.
Similarly, we say that a string w is a suffix of a string x,
denoted ![]() for some y
for some y
![]()
![]() *. It
follows from
*. It
follows from ![]() that |w|
that |w|
![]() |x|.
The empty string
|x|.
The empty string ![]() is both a
suffix and a prefix of every string. For example, we have ab
is both a
suffix and a prefix of every string. For example, we have ab ![]() abcca and cca
abcca and cca ![]() abcca. It is useful to note
that for any strings x and y and any character a, we have
abcca. It is useful to note
that for any strings x and y and any character a, we have ![]() if and only
if
if and only
if ![]() . Also note
that
. Also note
that ![]() are
transitive relations. The following lemma will be useful later.
are
transitive relations. The following lemma will be useful later.
Lemma 1
Proof See Figure 2 for a graphical proof.
For brevity of notation,
we shall denote the k-character prefix P[1 . . k] of the
pattern P[1 . . m] by Pk. Thus, P0
= ![]() and Pm
= P = P[1 . . m]. Similarly, we denote the k-character
prefix of the text T as Tk. Using this notation, we
can state the string-matching problem as that of finding all shifts s in
the range 0
and Pm
= P = P[1 . . m]. Similarly, we denote the k-character
prefix of the text T as Tk. Using this notation, we
can state the string-matching problem as that of finding all shifts s in
the range 0 ![]() s
s ![]() n - m
such that
n - m
such that ![]() .
.
In our pseudocode, we
allow two equal-length strings to be compared for equality as a primitive
operation. If the strings are compared from left to right and the comparison
stops when a mismatch is discovered, we assume that the time taken by such a
test is a linear function of the number of matching characters discovered. To
be precise, the test 'x = y' is assumed to take time ![]() (t +
1), where t is the length of the longest string z such that
(t +
1), where t is the length of the longest string z such that ![]() .
.
The naive algorithm finds all valid shifts using a loop that checks the condition P[1 . . m] = T[s + 1 . . s + m] for each of the n - m + 1 possible values of s.
NAIVE-STRING-MATCHER(T, P)The naive string-matching procedure can be interpreted graphically as sliding a 'template' containing the pattern over the text, noting for which shifts all of the characters on the template equal the corresponding characters in the text, as illustrated in Figure 3. The for loop beginning on line 3 considers each possible shift explicitly. The test on line 4 determines whether the current shift is valid or not; this test involves an implicit loop to check corresponding character positions until all positions match successfully or a mismatch is found. Line 5 prints out each valid shift s.

Procedure NAIVE-STRING MATCHER takes time ![]() ((n -
m + 1)m) in the worst case. For example, consider the text string
an (a string of n
a's) and
the pattern am. For each of the n
- m + 1 possible values of the shift s, the implicit loop on line
4 to compare corresponding characters must execute m times to validate
the shift. The worst-case running time is thus
((n -
m + 1)m) in the worst case. For example, consider the text string
an (a string of n
a's) and
the pattern am. For each of the n
- m + 1 possible values of the shift s, the implicit loop on line
4 to compare corresponding characters must execute m times to validate
the shift. The worst-case running time is thus ![]() ((n -
m + 1)m), which is
((n -
m + 1)m), which is ![]() (n2)
if m =
(n2)
if m = ![]() n
n ![]()
As we shall see, NAIVE-STRING MATCHER is not an optimal procedure for this problem. Indeed, in this chapter we shall show an algorithm with a worst-case running time of O(n + m). The naive string-matcher is inefficient because information gained about the text for one value of s is totally ignored in considering other values of s. Such information can be very valuable, however. For example, if P = aaab and we find that s = 0 is valid, then none of the shifts 1, 2, or 3 are valid, since T[4] = b. In the following sections, we examine several ways to make effective use of this sort of information.
Show the comparisons the naive string matcher makes for the pattern P = in the text T =
Show that the worst-case
time for the naive string matcher to find the first occurrence of a
pattern in a text is ![]() ((n -
m + 1)(m - 1)).
((n -
m + 1)(m - 1)).
Suppose that all characters in the pattern P are different. Show how to accelerate NAIVE-STRING MATCHER to run in time O(n) on an n-character text T.
Suppose that pattern P
and text T are randomly chosen strings of length m and n,
respectively, from the d-ary alphabet ![]() d
= , where d
d
= , where d ![]() 2. Show that
the expected number of character-to-character comparisons made by the
implicit loop in line 4 of the naive algorithm is
2. Show that
the expected number of character-to-character comparisons made by the
implicit loop in line 4 of the naive algorithm is
![]()
(Assume that the naive algorithm stops comparing characters for a given shift once a mismatch is found or the entire pattern is matched.) Thus, for randomly chosen strings, the naive algorithm is quite efficient.
Suppose we allow the pattern P to contain
occurrences of a gap character ![]() that can
match an arbitrary string of characters (even one of zero length). For
example, the pattern
that can
match an arbitrary string of characters (even one of zero length). For
example, the pattern ![]() occurs in
the text cabccbacbacab as
occurs in
the text cabccbacbacab as
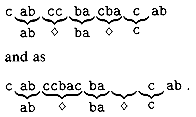
Note that the gap character may occur an arbitrary number of times in the pattern but is assumed not to occur at all in the text. Give a polynomial-time algorithm to determine if such a pattern P occurs in a given text T, and analyze the running time of your algorithm.
Rabin and Karp have proposed a string-matching algorithm that performs well in practice and that also generalizes to other algorithms for related problems, such as two-dimensional pattern matching. The worst-case running time of the Rabin-Karp algorithm is O((n - m + 1)m), but it has a good average-case running time.
This algorithm makes use of elementary number-theoretic notions such as the equivalence of two numbers modulo a third number. You may want to refer to Section 33.1 for the relevant definitions.
For expository purposes,
let us assume that ![]() = , so that each character is a
decimal digit. (In the general case, we can assume that each character is a
digit in radix-d notation, where d =
= , so that each character is a
decimal digit. (In the general case, we can assume that each character is a
digit in radix-d notation, where d = ![]()
![]()
![]() .) We can
then view a string of k consecutive characters as representing a length-k
decimal number. The character string thus corresponds to the decimal number 31,415. Given the dual
interpretation of the input characters as both graphical symbols and digits, we
find it convenient in this section to denote them as we would digits, in our
standard text font.
.) We can
then view a string of k consecutive characters as representing a length-k
decimal number. The character string thus corresponds to the decimal number 31,415. Given the dual
interpretation of the input characters as both graphical symbols and digits, we
find it convenient in this section to denote them as we would digits, in our
standard text font.
Given a pattern P[1 . . m], we let p denote its corresponding decimal value. In a similar manner, given a text T[1 . . n], we let ts denote the decimal value of the length-m substring T[s + 1 . . s + m], for s = 0, 1, . . . , n - m. Certainly, ts = p if and only if T[s + 1 . . s + m] = P[1 . . m]; thus, s is a valid shift if and only if ts = p. If we could compute p in time O(m) and all of the ti values in a total of O(n) time, then we could determine all valid shifts s in time O(n) by comparing p with each of the ts's. (For the moment, let's not worry about the possibility that p and the ts's might be very large numbers.)
We can compute p in time O(m) using Horner's rule (see Section 32.1):
p = P[m] + 10 (P[m - 1] + 10(P[m - 2] + . . . + 10(P[2] + 10P[1]) . . . )).The value t0 can be similarly computed from T[1 . . m] in time O(m).
To compute the remaining values t1, t2, . . . , tn-m in time O(n - m), it suffices to observe that ts + 1 can be computed from ts in constant time, since
ts = 10(ts - 10m - 1T[s + 1]) + T[s + m + 1].For example, if m= 5 and ts = 31415, then we wish to remove the high-order digit T[s + 1] = 3 and bring in the new low-order digit (suppose it is T[s + 5 + 1] = 2) to obtain
tsSubtracting 10m-1 T[s+1] removes the high-order digit from ts, multiplying the result by 10 shifts the number left one position, and adding T[s + m + 1] brings in the appropriate low-order digit. If the constant 10m is precomputed (which can be done in time O(1g m) using the techniques of Section 33.6, although for this application a straightforward O(m) method is quite adequate), then each execution of equation (1) takes a constant number of arithmetic operations. Thus, p and t0, t1, . . . , tn-m can all be computed in time O(n + m), and we can find all occurrences of the pattern P[1 . . m] in the text T[1 . . n] in time O(n + m).
The only difficulty with this procedure is that p and ts may be too large to work with conveniently. If P contains m characters, then assuming that each arithmetic operation on p (which is m digits long) takes 'constant time' is unreasonable. Fortunately, there is a simple cure for this problem, as shown in Figure 4 : compute p and the ts's modulo a suitable modulus q. Since the computation of p, t0, and the recurrence (1) can all be performed modulo q, we see that p and all the ts's can be computed modulo q in time O(n + m). The modulus q is typically chosen as a prime such that 10q just fits within one computer word, which allows all of the necessary computations to be performed with single-precision arithmetic.
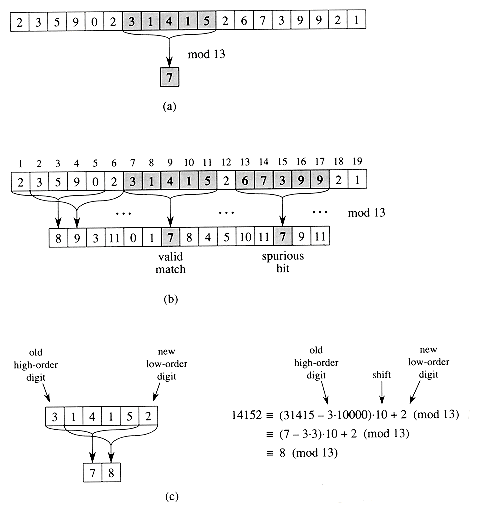
In general, with a d-ary alphabet , we choose q so that d q fits within a computer word and adjust the recurrence equation (1) to work modulo q, so that it becomes
ts = (d(ts - T[s + 1]h) + T[s + m + 1]) mod q ,where h ![]() dm-1
(mod q) is the value of the digit '1' in the high-order
position of an m-digit text window.
dm-1
(mod q) is the value of the digit '1' in the high-order
position of an m-digit text window.
The following procedure
makes these ideas precise. The inputs to the procedure are the text T,
the pattern P, the radix d to use (which is typically taken to be
|![]() |), and the
prime q to use.
|), and the
prime q to use.
The procedure RABIN KARP MATCHER works as follows. All characters are interpreted as radix-d digits. The subscripts on t are provided only for clarity; the program works correctly if all the subscripts are dropped. Line 3 initializes h to the value of the high-order digit position of an m-digit window. Lines 4-8 compute p as the value of P[1 . . m] mod q and t0 as the value of T[1 . . m] mod q. The for loop beginning on line 9 iterates through all possible shifts s. The loop has the following invariant: whenever line 10 is executed, ts = T[s + 1 . . s + m] mod q. If p = ts in line 10 (a 'hit'), then we check to see if P[1 . . m] = T[s + 1 . . s + m] in line 11 to rule out the possibility of a spurious hit. Any valid shifts found are printed out on line 12. If s < n - m (checked in line 13), then the for loop is to be executed at least one more time, and so line 14 is first executed to ensure that the loop invariant holds when line 10 is again reached. Line 14 computes the value of ts+1 mod q from the value of ts mod q in constant time using equation (2) directly.
The running time of RABIN KARP MATCHER is ![]() ((n -
m + 1)m) in the worst case, since (like the naive string-matching
algorithm) the Rabin-Karp algorithm explicitly verifies every valid shift. If P
= am and T = an, then the
verifications take time
((n -
m + 1)m) in the worst case, since (like the naive string-matching
algorithm) the Rabin-Karp algorithm explicitly verifies every valid shift. If P
= am and T = an, then the
verifications take time ![]() ((n -
m + 1)m), since each of the n - m + 1 possible
shifts is valid. (Note also that the computation of dm-1
mod q on line 3 and the loop on lines 6-8 take time O(m) =
O((n - m + 1 )m).)
((n -
m + 1)m), since each of the n - m + 1 possible
shifts is valid. (Note also that the computation of dm-1
mod q on line 3 and the loop on lines 6-8 take time O(m) =
O((n - m + 1 )m).)
In many applications, we
expect few valid shifts (perhaps O(1) of them), and so the expected
running time of the algorithm is O(n + m) plus the time
required to process spurious hits. We can base a heuristic analysis on the
assumption that reducing values modulo q acts like a random mapping from
![]() * to Zq.
(See the discussion on the use of division for hashing in Section 12.3.1. It is
difficult to formalize and prove such an assumption, although one viable
approach is to assume that q is chosen randomly from integers of the
appropriate size. We shall not pursue this formalization here.) We can then
expect that the number of spurious hits is O(n/q), since
the chance that an arbitrary ts will be equivalent to p,
modulo q, can be estimated as 1/q. The expected amount of time
taken by the Rabin-Karp algorithm is then
* to Zq.
(See the discussion on the use of division for hashing in Section 12.3.1. It is
difficult to formalize and prove such an assumption, although one viable
approach is to assume that q is chosen randomly from integers of the
appropriate size. We shall not pursue this formalization here.) We can then
expect that the number of spurious hits is O(n/q), since
the chance that an arbitrary ts will be equivalent to p,
modulo q, can be estimated as 1/q. The expected amount of time
taken by the Rabin-Karp algorithm is then
where v is the
number of valid shifts. This running time is O(n) if we choose q
![]() m.
That is, if the expected number of valid shifts is small (O(1)) and the
prime q is chosen to be larger than the length of the pattern, then we
can expect the Rabin-Karp procedure to run in time O(n + m).
m.
That is, if the expected number of valid shifts is small (O(1)) and the
prime q is chosen to be larger than the length of the pattern, then we
can expect the Rabin-Karp procedure to run in time O(n + m).
Working modulo q = 11, how many spurious hits does the Rabin-Karp matcher encounter in the text T = 3141592653589793 when looking for the pattern P = 26?
How would you extend the Rabin-Karp method to the problem of searching a text string for an occurrence of any one of a given set of k patterns?
Show how to extend the Rabin-Karp method to handle the problem of looking for a given m X m pattern in an n X n array of characters. (The pattern may be shifted vertically and horizontally, but it may not be rotated.)
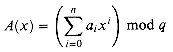
and Bob similarly
evaluates B(x). Prove that if A ![]() B,
there is at most one chance in 1000 that A(x) = B(x),
whereas if the two files are the same, A(x) is necessarily the
same as B(x). (Hint: See Exercise 33.4-4.)
B,
there is at most one chance in 1000 that A(x) = B(x),
whereas if the two files are the same, A(x) is necessarily the
same as B(x). (Hint: See Exercise 33.4-4.)
We begin this section with the definition of a finite automaton. We then examine a special string-matching automaton and show how it can be used to find occurrences of a pattern in a text. This discussion includes details on how to simulate the behavior of a string-matching automaton on a given text. Finally, we shall show how to construct the string-matching automaton for a given input pattern.
A finite automaton M
is a 5-tuple (Q, q0, A, ![]() ,
, ![]() ), where
), where
![]() Q is a finite set of states,
Q is a finite set of states,
![]() q
q ![]() Q is
the start state,
Q is
the start state,
![]() A
A ![]() Q is
a distinguished set of accepting states,
Q is
a distinguished set of accepting states,
![]()
![]() is a finite input
alphabet,
is a finite input
alphabet,
![]()
![]() is a
function from Q X
is a
function from Q X ![]() into Q,
called the transition function of M.
into Q,
called the transition function of M.
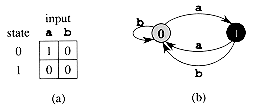
The finite automaton begins in
state q0 and reads the characters of its input string one at
a time. If the automaton is in state q and reads input character a,
it moves ('makes a transition') from state q to state ![]() (q, a).
Whenever its current state q is a member of A, the machine M
is said to have accepted the string read so far. An input that is
not accepted is said to be rejected. Figure 5 illustrates these
definitions with a simple two-state automaton.
(q, a).
Whenever its current state q is a member of A, the machine M
is said to have accepted the string read so far. An input that is
not accepted is said to be rejected. Figure 5 illustrates these
definitions with a simple two-state automaton.
A finite automaton M induces a function
, called the final-state function, from ![]() * to Q
such that (w) is the state M ends up in after scanning the
string w. Thus, M accepts a string w if and only if (w)
* to Q
such that (w) is the state M ends up in after scanning the
string w. Thus, M accepts a string w if and only if (w)
![]() A.
The function is defined by the recursive relation
A.
The function is defined by the recursive relation
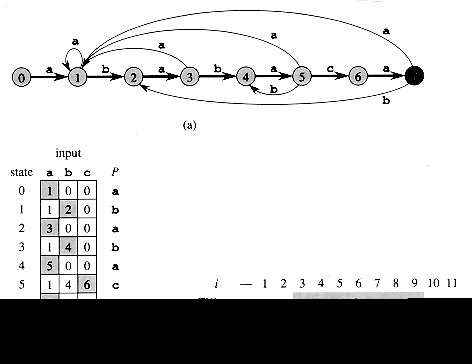
There is a string-matching automaton for every pattern P; this automaton must be constructed from the pattern in a preprocessing step before it can be used to search the text string. Figure 6 illustrates this construction for the pattern P = ababaca. From now on, we shall assume that P is a given fixed pattern string; for brevity, we shall not indicate the dependence upon P in our notation.
![]()
The suffix function ![]() is well
defined since the empty string P0 =
is well
defined since the empty string P0 = ![]() is a suffix
of every string. As examples, for the pattern P = ab, we have
is a suffix
of every string. As examples, for the pattern P = ab, we have ![]() (
(![]() ) = 0,
) = 0, ![]() (ccaca) = 1, and
(ccaca) = 1, and ![]() (ccab) = 2. For a pattern P
of length m, we have
(ccab) = 2. For a pattern P
of length m, we have ![]() (x)
= m if and only if
(x)
= m if and only if ![]() . It follows
from the definition of the suffix function that if
. It follows
from the definition of the suffix function that if ![]() , then
, then ![]() (x)
(x)
![]()
![]() (y).
(y).
We define the string-matching automaton corresponding to a given pattern P[1 . . m] as follows.
![]() The state set Q is . The start state q0
is state 0, and state m is the only accepting state.
The state set Q is . The start state q0
is state 0, and state m is the only accepting state.
![]() The transition function
The transition function ![]() is defined
by the following equation, for any state q and character a:
is defined
by the following equation, for any state q and character a:
Here is an intuitive
rationale for defining ![]() (q, a)
=
(q, a)
= ![]() (Pq
a). The machine maintains as an invariant of its operation that
(Pq
a). The machine maintains as an invariant of its operation that
this result is proved as
Theorem 4 below. In words, this means that after scanning the first i
characters of the text string T, the machine is in state ![]() (Ti)
= q, where q =
(Ti)
= q, where q = ![]() (Ti)
is the length of the longest suffix of Ti that is also a
prefix of the pattern P. If the next character scanned is T[i
+ 1] = a, then the machine should make a transition to state
(Ti)
is the length of the longest suffix of Ti that is also a
prefix of the pattern P. If the next character scanned is T[i
+ 1] = a, then the machine should make a transition to state ![]() (Ti
+ 1) =
(Ti
+ 1) = ![]() (Tia).
The proof of the theorem shows that
(Tia).
The proof of the theorem shows that ![]() (Tia)
=
(Tia)
= ![]() (Pqa).
That is, to compute the length of the longest suffix of Tia
that is a prefix of P, we can compute the longest suffix of Pqa
that is a prefix of P. At each state, the machine only needs to know the
length of the longest prefix of P that is a suffix of what has been read
so far. Therefore, setting
(Pqa).
That is, to compute the length of the longest suffix of Tia
that is a prefix of P, we can compute the longest suffix of Pqa
that is a prefix of P. At each state, the machine only needs to know the
length of the longest prefix of P that is a suffix of what has been read
so far. Therefore, setting ![]() (q, a) =
(q, a) = ![]() (Pqa)
maintains the desired invariant (4). This informal argument will be made
rigorous shortly.
(Pqa)
maintains the desired invariant (4). This informal argument will be made
rigorous shortly.
In the string-matching
automaton of Figure 6, for example, we have ![]() (5, b) = 4. This follows from the
fact that if the automaton reads a b in state q = 5, then Pqb ababab, and the longest prefix of P that is also a suffix of ababab is P4
= abab
(5, b) = 4. This follows from the
fact that if the automaton reads a b in state q = 5, then Pqb ababab, and the longest prefix of P that is also a suffix of ababab is P4
= abab
To clarify the operation
of a string-matching automaton, we now give a simple, efficient program for
simulating the behavior of such an automaton (represented by its transition
function ![]() ) in finding
occurrences of a pattern P of length m in an input text T[1
. . n]. As for any string-matching automaton for a pattern of length m,
the state set Q is , the start state is 0, and
the only accepting state is state m.
) in finding
occurrences of a pattern P of length m in an input text T[1
. . n]. As for any string-matching automaton for a pattern of length m,
the state set Q is , the start state is 0, and
the only accepting state is state m.
The simple loop structure
of FINITE AUTOMATON MATCHER implies that its
running time on a text string of length n is O(n). This
running time, however, does not include the time required to compute the
transition function ![]() . We address
this problem later, after proving that the procedure FINITE AUTOMATON-MATCHER operates correctly.
. We address
this problem later, after proving that the procedure FINITE AUTOMATON-MATCHER operates correctly.
Consider the operation of
the automaton on an input text T[1 . . n]. We shall prove that
the automaton is in state ![]() (Tj)
after scanning character T[i]. Since
(Tj)
after scanning character T[i]. Since ![]() (Ti)
= m if and only if
(Ti)
= m if and only if ![]() , the
machine is in the accepting state m if and only if the pattern P
has just been scanned. To prove this result, we make use of the following two
lemmas about the suffix function
, the
machine is in the accepting state m if and only if the pattern P
has just been scanned. To prove this result, we make use of the following two
lemmas about the suffix function ![]() .
.
Lemma 2
For any string x and character a,
we have ![]() (xa)
(xa)
![]()
![]() (x)
+ 1.
(x)
+ 1.
Proof Referring to Figure 7, let r = ![]() (xa).
If r = 0, then the conclusion r
(xa).
If r = 0, then the conclusion r ![]()
![]() (x) +
1 is trivially satisfied, by the nonnegativity of
(x) +
1 is trivially satisfied, by the nonnegativity of ![]() (x).
So assume that r > 0. Now,
(x).
So assume that r > 0. Now, ![]() , by the
definition of
, by the
definition of ![]() . Thus,
. Thus, ![]() , by
dropping the a from the end of Pr and from the end of xa.
Therefore, r - 1
, by
dropping the a from the end of Pr and from the end of xa.
Therefore, r - 1 ![]()
![]() (x),
since
(x),
since ![]() (x)
is largest k such that
(x)
is largest k such that ![]() .
.
Lemma 3
For any string x and character a,
if q = ![]() (x),
then
(x),
then ![]() (xa)
=
(xa)
= ![]() (Pqa).
(Pqa).
Proof From the definition of ![]() , we have
, we have ![]() . As Figure 8
shows,
. As Figure 8
shows, ![]() . If we let r
=
. If we let r
= ![]() (xa),
then r
(xa),
then r ![]() q + 1
by Lemma 2. Since
q + 1
by Lemma 2. Since ![]() , and
, and ![]() Pr
Pr![]()
![]()
![]() Pqa
Pqa![]() , Lemma 1
implies that
, Lemma 1
implies that ![]() . Therefore,
r
. Therefore,
r ![]()
![]() (Pqa),
that is,
(Pqa),
that is, ![]() (xa)
(xa) ![]()
![]() (Pqa).
But we also have
(Pqa).
But we also have ![]() (Pqa)
(Pqa)
![]()
![]() (xa),
since
(xa),
since ![]() . Thus,
. Thus, ![]() (xa)
=
(xa)
= ![]() (Pqa).
(Pqa).
We are now ready to prove our main theorem characterizing the behavior of a string-matching automaton on a given input text. As noted above, this theorem shows that the automaton is merely keeping track, at each step, of the longest prefix of the pattern that is a suffix of what has been read so far.
Theorem 4
If ![]() is the
final-state function of a string-matching automaton for a given pattern P
and T[1 . . n] is an input text for the automaton, then
is the
final-state function of a string-matching automaton for a given pattern P
and T[1 . . n] is an input text for the automaton, then
Proof The proof is by induction on i. For i = 0, the theorem is
trivially true, since T0 = ![]() . Thus,
. Thus, ![]() .
.
Now, we assume that ![]() and prove
that
and prove
that ![]() . Let q
denote
. Let q
denote ![]() , and let a
denote T[i + 1]. Then,
, and let a
denote T[i + 1]. Then,

By induction, the theorem is proved.
By Theorem 4, if the
machine enters state q on line 4, then q is the largest value
such that ![]() . Thus, we
have q = m on line 5 if and only if an occurrence of the pattern P
has just been scanned. We conclude that FINITE AUTOMATON MATCHER
operates correctly.
. Thus, we
have q = m on line 5 if and only if an occurrence of the pattern P
has just been scanned. We conclude that FINITE AUTOMATON MATCHER
operates correctly.
The following procedure computes the
transition function ![]() from a
given pattern P[1 . . m].
from a
given pattern P[1 . . m].
![]()
This procedure computes ![]() (q, a)
in a straightforward manner according to its definition. The nested loops
beginning on lines 2 and 3 consider all states q and characters a,
and lines 4-7 set
(q, a)
in a straightforward manner according to its definition. The nested loops
beginning on lines 2 and 3 consider all states q and characters a,
and lines 4-7 set ![]() (q, a)
to be the largest k such that
(q, a)
to be the largest k such that ![]() . The code
starts with the largest conceivable value of k, which is min(m, q
+ 1), and decreases k until
. The code
starts with the largest conceivable value of k, which is min(m, q
+ 1), and decreases k until ![]() .
.
The running time of COMPUTE TRANSITION FUNCTION is O(m3![]()
![]()
![]() ), because
the outer loops contribute a factor of m
), because
the outer loops contribute a factor of m ![]()
![]()
![]() , the inner repeat
loop can run at most m + 1 times, and the test
, the inner repeat
loop can run at most m + 1 times, and the test ![]() on line 6
can require comparing up to m characters. Much faster procedures exist;
the time required to compute
on line 6
can require comparing up to m characters. Much faster procedures exist;
the time required to compute ![]() from P
can be improved to O(m
from P
can be improved to O(m![]()
![]()
![]() ) by
utilizing some cleverly computed information about the pattern P (see
Exercise 4-6). With this improved procedure for computing
) by
utilizing some cleverly computed information about the pattern P (see
Exercise 4-6). With this improved procedure for computing ![]() , the total
running time to find all occurrences of a length-m pattern in a length-n
text over an alphabet
, the total
running time to find all occurrences of a length-m pattern in a length-n
text over an alphabet ![]() is O(n
+ m
is O(n
+ m![]()
![]()
![]() ).
).
Construct the string-matching automaton for the pattern P = aabab and illustrate its operation on the text string T = aaababaabaababaab
Draw a state-transition
diagram for a string-matching automaton for the pattern ababbabbababbababbabb over the
alphabet ![]() = .
= .
We call a pattern P nonoverlappable
if ![]() implies k
= 0 or k = q. Describe the state-transition diagram of the
string-matching automaton for a nonoverlappable pattern.
implies k
= 0 or k = q. Describe the state-transition diagram of the
string-matching automaton for a nonoverlappable pattern.
Given two patterns P and P', describe how to construct a finite automaton that determines all occurrences of either pattern. Try to minimize the number of states in your automaton.
Given a pattern P containing gap
characters (see Exercise 1-5), show how to build a finite automaton that can
find an occurrence of P in a text T in O(n) time,
where n = ![]() T
T![]() .
.
We now present a linear-time
string-matching algorithm due to Knuth, Morris, and Pratt. Their algorithm
achieves a ![]() (n + m)
running time by avoiding the computation of the transition function
(n + m)
running time by avoiding the computation of the transition function ![]() altogether,
and it does the pattern matching using just an auxiliary function
altogether,
and it does the pattern matching using just an auxiliary function ![]() [1 . . m]
precomputed from the pattern in time O(m). The array
[1 . . m]
precomputed from the pattern in time O(m). The array ![]() allows the
transition function
allows the
transition function ![]() to be computed
efficiently (in an amortized sense) 'on the fly' as needed. Roughly
speaking, for any state q = 0, 1, . . . , m,and any character a
to be computed
efficiently (in an amortized sense) 'on the fly' as needed. Roughly
speaking, for any state q = 0, 1, . . . , m,and any character a
![]()
![]() , the value
, the value ![]() [q]
contains the information that is independent of a and is needed to
compute
[q]
contains the information that is independent of a and is needed to
compute ![]() (q, a).
(This remark will be clarified shortly.) Since the array
(q, a).
(This remark will be clarified shortly.) Since the array ![]() has only m
entries, whereas
has only m
entries, whereas ![]() has O(m
has O(m
![]()
![]()
![]() ) entries,
we save a factor of
) entries,
we save a factor of ![]() in the
preprocessing by computing
in the
preprocessing by computing ![]() rather than
rather than ![]() .
.
The prefix function for a pattern
encapsulates knowledge about how the pattern matches against shifts of itself.
This information can be used to avoid testing useless shifts in the naive
pattern-matching algorithm or to avoid the precomputation of ![]() for a
string-matching automaton.
for a
string-matching automaton.
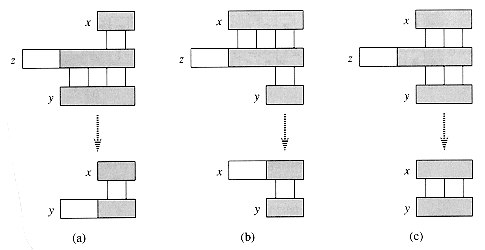
Consider the operation of the naive string matcher. Figure 9(a) shows a particular shift s of a template containing the pattern P = ababaca against a text T. For this example, q = 5 of the characters have matched successfully, but the 6th pattern character fails to match the corresponding text character. The information that q characters have matched successfully determines the corresponding text characters. Knowing these q text characters allows us to determine immediately that certain shifts are invalid. In the example of the figure, the shift s + 1 is necessarily invalid, since the first pattern character, an a, would be aligned with a text character that is known to match with the second pattern character, a b. The shift s + 2 shown in part (b) of the figure, however, aligns the first three pattern characters with three text characters that must necessarily match. In general, it is useful to know the answer to the following question:
Given that pattern characters P[1 . . q] match text characters T[s + 1 . . s + q], what is the least shift s' > s such that
P[1 . . k] = T[s' 1 . . s' k],where s' + k = s + q?
Such a shift s' is the first shift greater than s that is not necessarily invalid due to our knowledge of T[s + 1 . . s + q]. In the best case, we have that s' = s + q, and shifts s + 1, s + 2, . . . , s + q - 1 are all immediately ruled out. In any case, at the new shift s' we don't need to compare the first k characters of P with the corresponding characters of T, since we are guaranteed that they match by equation (5).
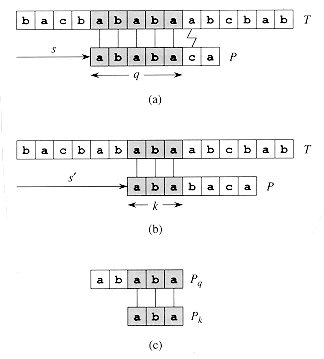
The necessary information
can be precomputed by comparing the pattern against itself, as illustrated in
Figure 9(c). Since T[s' + 1 . . s' + k] is
part of the known portion of the text, it is a suffix of the string Pq.
Equation (5) can therefore be interpreted as asking for the largest k
< q such that ![]() Then, s' = s + (q
- k) is the next potentially valid shift. It turns out to be convenient to
store the number k of matching characters at the new shift s',
rather than storing, say, s' - s. This information can be used to
speed up both the naive string-matching algorithm and the finite-automaton
matcher.
Then, s' = s + (q
- k) is the next potentially valid shift. It turns out to be convenient to
store the number k of matching characters at the new shift s',
rather than storing, say, s' - s. This information can be used to
speed up both the naive string-matching algorithm and the finite-automaton
matcher.
We formalize the
precomputation required as follows. Given a pattern P[1 . . m],
the prefix function for the pattern P is the function ![]() :
: ![]() such that
such that
![]()
That is, ![]() [q]
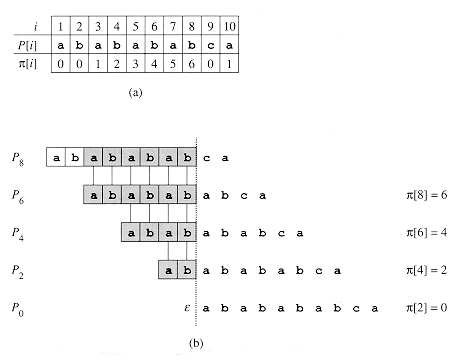
is the length of the longest prefix of P that is a proper suffix of Pq.
As another example, Figure 10(a) gives the complete prefix function
[q]
is the length of the longest prefix of P that is a proper suffix of Pq.
As another example, Figure 10(a) gives the complete prefix function ![]() for the
pattern ababababca
for the
pattern ababababca
The Knuth-Morris-Pratt
matching algorithm is given in pseudocode below as the procedure KMP-MATCHER. It is mostly modeled
after FINITE AUTOMATON MATCHER, as we shall see. KMP-MATCHER calls the auxiliary
procedure COMPUTE PREFIX FUNCTION to compute ![]() .
.
We begin with an analysis of the running times of these procedures. Proving these procedures correct will be more complicated.
The running time of COMPUTE PREFIX FUNCTION is O(m),
using an amortized analysis (see Chapter 18). We associate a potential of k
with the current state k of the algorithm. This potential has an initial
value of 0, by line 3. Line 6 decreases k whenever it is executed, since
![]() [k]
< k. Since
[k]
< k. Since ![]() [k]
[k] ![]() 0 for all k,
however, k can never become negative. The only other line that affects k
is line 8, which increases k by at most one during each execution of the
for loop body. Since k < q upon entering the for
loop, and since q is incremented in each iteration of the for
loop body, k < q always holds. (This justifies the claim that
0 for all k,
however, k can never become negative. The only other line that affects k
is line 8, which increases k by at most one during each execution of the
for loop body. Since k < q upon entering the for
loop, and since q is incremented in each iteration of the for
loop body, k < q always holds. (This justifies the claim that ![]() [q]
< q as well, by line 9.) We can pay for each execution of the while
loop body on line 6 with the corresponding decrease in the potential function,
since
[q]
< q as well, by line 9.) We can pay for each execution of the while
loop body on line 6 with the corresponding decrease in the potential function,
since ![]() [k]
< k. Line 8 increases the potential function by at most one, so that
the amortized cost of the loop body on lines 5-9 is O(1). Since the
number of outer-loop iterations is O(m), and since the final
potential function is at least as great as the initial potential function, the
total actual worst-case running time of COMPUTE PREFIX FUNCTION is O(m).
[k]
< k. Line 8 increases the potential function by at most one, so that
the amortized cost of the loop body on lines 5-9 is O(1). Since the
number of outer-loop iterations is O(m), and since the final
potential function is at least as great as the initial potential function, the
total actual worst-case running time of COMPUTE PREFIX FUNCTION is O(m).
The Knuth-Morris-Pratt algorithm runs in time O(m + n). The call of COMPUTE PREFIX FUNCTION takes O(m) time as we have just seen, and a similar amortized analysis, using the value of q as the potential function, shows that the remainder of KMP-MATCHER takes O(n) time.
Compared to FlNITE AUTOMATON MATCHER, by using ![]() rather than
rather than ![]() , we have
reduced the time for preprocessing the pattern from O(m |
, we have
reduced the time for preprocessing the pattern from O(m |![]() |) to O(m),
while keeping the actual matching time bounded by O(m + n).
|) to O(m),
while keeping the actual matching time bounded by O(m + n).
We start with an essential
lemma showing that by iterating the prefix function ![]() , we can
enumerate all the prefixes Pk that are suffixes of a given
prefix Pq. Let
, we can
enumerate all the prefixes Pk that are suffixes of a given
prefix Pq. Let
where ![]() i[q]
is defined in terms of functional composition, so that
i[q]
is defined in terms of functional composition, so that ![]() 0[q]
= q and
0[q]
= q and ![]() i+1[q]
=
i+1[q]
= ![]() [
[![]() i[q]]
for i > 1, and where it is understood that the sequence in
i[q]]
for i > 1, and where it is understood that the sequence in ![]() *[q]
stops when
*[q]
stops when ![]() t[q]
= 0 is reached.
t[q]
= 0 is reached.
Lemma 5
Let P be a pattern of length m
with prefix function ![]() . Then, for q
= 1, 2, . . . , m, we have
. Then, for q
= 1, 2, . . . , m, we have ![]() .
.
Proof We first prove that
iIf i ![]()
![]() *[q],
then i =
*[q],
then i = ![]() u[q]
for some u. We prove equation (6) by induction on u. For u
= 0, we have i = q, and the claim follows since
u[q]
for some u. We prove equation (6) by induction on u. For u
= 0, we have i = q, and the claim follows since ![]() . Using the
relation
. Using the
relation ![]() and the transitivity
of
and the transitivity
of ![]() establishes
the claim for all i in
establishes
the claim for all i in ![]() *[q].
Therefore,
*[q].
Therefore, ![]() .
.
We prove that ![]() by
contradiction. Suppose to the contrary that there is an integer in the set
by
contradiction. Suppose to the contrary that there is an integer in the set ![]() , and let j
be the largest such value. Because q is in
, and let j
be the largest such value. Because q is in ![]() , we have j
< q, and so we let j' denote the smallest integer in
, we have j
< q, and so we let j' denote the smallest integer in ![]() *[q]
that is greater than j. (We can choose j' = q if there is
no other number in
*[q]
that is greater than j. (We can choose j' = q if there is
no other number in ![]() *[q]
that is greater than j.) We have
*[q]
that is greater than j.) We have ![]() because
because ![]() because j'
because j'
![]()
![]() *[q];
thus,
*[q];
thus, ![]() by Lemma 1.
Moreover, j is the largest such value with this property. Therefore, we
must have
by Lemma 1.
Moreover, j is the largest such value with this property. Therefore, we
must have ![]() [j']
= j and thus j
[j']
= j and thus j ![]()
![]() *[q].
This contradiction proves the lemma.
*[q].
This contradiction proves the lemma.
Figure 10 illustrates this lemma.
The algorithm COMPUTE PREFIX FUNCTION computes ![]() [q]
in order for q = 1, 2, . . . , m. The computation of
[q]
in order for q = 1, 2, . . . , m. The computation of ![]() [1] = 0 in
line 2 of COMPUTE PREFIX FUNCTION is certainly correct,
since
[1] = 0 in
line 2 of COMPUTE PREFIX FUNCTION is certainly correct,
since ![]() [q]
< q for all q. The following lemma and its corollary will be
used to prove that COMPUTE PREFIX FUNCTION computes
[q]
< q for all q. The following lemma and its corollary will be
used to prove that COMPUTE PREFIX FUNCTION computes ![]() [q]
correctly for q > 1.
[q]
correctly for q > 1.
Lemma 6
Let P be a pattern
of length m, and let ![]() be the
prefix function for P. For q = 1, 2, . . . , m, if
be the
prefix function for P. For q = 1, 2, . . . , m, if ![]() [q]
> 0, then
[q]
> 0, then ![]() [q] - 1
[q] - 1
![]()
![]() *[q -
1].
*[q -
1].
Proof If k = ![]() [q]
> 0, then
[q]
> 0, then ![]() (by dropping
the last character from Pk and Pq). By
Lemma 5, therefore, k - l
(by dropping
the last character from Pk and Pq). By
Lemma 5, therefore, k - l ![]()
![]() *[q -
1].
*[q -
1].
For q = 2, 3, . .
. , m, define the subset Eq-1 ![]()
![]() *[q -
1] by
*[q -
1] by
The set Eq-1
consists of the values k for which ![]() (by Lemma 5);
because P[k + 1] = P[q], it is also the case that
for these values of k,
(by Lemma 5);
because P[k + 1] = P[q], it is also the case that
for these values of k, ![]() .
Intuitively, Eq - 1 consists of those values k
.
Intuitively, Eq - 1 consists of those values k
![]()
![]() *[q -
1] such that we can extend Pk to Pk+1
and get a suffix of Pq.
*[q -
1] such that we can extend Pk to Pk+1
and get a suffix of Pq.
Corollary 7
Let P be a pattern
of length m, and let ![]() be the
prefix function for P. For q = 2, 3, . . . , m,
be the
prefix function for P. For q = 2, 3, . . . , m,
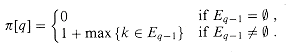
Proof If r = ![]() [q],
then
[q],
then ![]() , and so r
, and so r
![]() 1 implies P[r]
= P[q]. By Lemma 6, therefore, if r
1 implies P[r]
= P[q]. By Lemma 6, therefore, if r ![]() 1, then
1, then
But the set maximized
over is just Eq-1, so that r = 1 + max and Eq-1 is nonempty. If r = 0, there is no k
![]()
![]() *[q -
1] for which we can extend Pk to Pk and get a suffix of Pq, since then we
would have
*[q -
1] for which we can extend Pk to Pk and get a suffix of Pq, since then we
would have ![]() [q]
> 0. Thus,
[q]
> 0. Thus, ![]() .
.
We now finish the proof
that COMPUTE PREFIX FUNCTION computes ![]() correctly.
In the procedure COMPUTE PREFIX FUNCTION, at the start of each
iteration of the for loop of lines 4-9, we have that k =
correctly.
In the procedure COMPUTE PREFIX FUNCTION, at the start of each
iteration of the for loop of lines 4-9, we have that k = ![]() [q -
1]. This condition is enforced by lines 2 and 3 when the loop is first entered,
and it remains true in each successive iteration because of line 9. Lines 5-8
adjust k so that it now becomes the correct value of
[q -
1]. This condition is enforced by lines 2 and 3 when the loop is first entered,
and it remains true in each successive iteration because of line 9. Lines 5-8
adjust k so that it now becomes the correct value of ![]() [q].
The loop on lines 5-6 searches through all values k
[q].
The loop on lines 5-6 searches through all values k ![]()
![]() *[q -
1] until one is found for which P[k + 1] = P[q]; at
that point, we have that k is the largest value in the set Eq-1,
so that, by Corollary 7, we can set
*[q -
1] until one is found for which P[k + 1] = P[q]; at
that point, we have that k is the largest value in the set Eq-1,
so that, by Corollary 7, we can set ![]() [q]
to k + 1. If no such k is found, k = 0 in lines 7-9, and
[q]
to k + 1. If no such k is found, k = 0 in lines 7-9, and ![]() [q]
is set to 0. This completes our proof of the correctness of
COMPUTE-PREFIX-FUNCTION.
[q]
is set to 0. This completes our proof of the correctness of
COMPUTE-PREFIX-FUNCTION.
The procedure KMP-MATCHER can be viewed as a
reimplementation of the procedure FINlTE AUTOMATON MATCHER.
Specifically, we shall prove that the code on lines 6-9 of KMP-MATCHER is equivalent to line 4
of FINITE AUTOMATON MATCHER, which sets q to
![]() (q,T[i]).
Instead of using a stored value of
(q,T[i]).
Instead of using a stored value of ![]() (q, T[i]),
however, this value is recomputed as necessary from
(q, T[i]),
however, this value is recomputed as necessary from ![]() . Once we
have argued that KMP-MATCHER simulates the behavior of FINITE AUTOMATON MATCHER,
the correctness of KMP-MATCHER follows from the correctness of FINITE AUTOMATON MATCHER
(though we shall see in a moment why line 12 in KMP-MATCHER is necessary).
. Once we
have argued that KMP-MATCHER simulates the behavior of FINITE AUTOMATON MATCHER,
the correctness of KMP-MATCHER follows from the correctness of FINITE AUTOMATON MATCHER
(though we shall see in a moment why line 12 in KMP-MATCHER is necessary).
The correctness of KMP-MATCHER follows from the claim
that either ![]() (q, T[i])
= 0 or else
(q, T[i])
= 0 or else ![]() (q, T[i])
- 1
(q, T[i])
- 1 ![]()
![]() *[q].
To check this claim, let k =
*[q].
To check this claim, let k = ![]() (q, T[i]).
Then,
(q, T[i]).
Then, ![]() by the
definitions of
by the
definitions of ![]() and
and ![]() . Therefore,
either k = 0 or else k
. Therefore,
either k = 0 or else k ![]() 1 and
1 and ![]() by dropping
the last character from both Pk and PqT[i]
(in which case k - 1
by dropping
the last character from both Pk and PqT[i]
(in which case k - 1 ![]()
![]() *[q]).
Therefore, either k = 0 or k - 1
*[q]).
Therefore, either k = 0 or k - 1 ![]()
![]() *[q],
proving the claim.
*[q],
proving the claim.
The claim is used as
follows. Let q' denote the value of q when line 6 is entered. We
use the equivalence ![]() to justify
the iteration q
to justify
the iteration q ![]()
![]() [q]
that enumerates the elements of
[q]
that enumerates the elements of ![]() . Lines 6-9
determine
. Lines 6-9
determine ![]() (q',
T[i]) by examining the elements of
(q',
T[i]) by examining the elements of ![]() *[q']
in decreasing order. The code uses the claim to begin with q =
*[q']
in decreasing order. The code uses the claim to begin with q = ![]() (Ti -
1) =
(Ti -
1) = ![]() (Ti ) and perform the iteration q
(Ti ) and perform the iteration q ![]()
![]() [q]
until a q is found such that q = 0 or P[q + 1] = T[i].
In the former case,
[q]
until a q is found such that q = 0 or P[q + 1] = T[i].
In the former case, ![]() (q',
T[i]) = 0; in the latter case, q is the maximum element in
Eq', so that
(q',
T[i]) = 0; in the latter case, q is the maximum element in
Eq', so that ![]() (q', T[i])
= q + 1 by Corollary 7.
(q', T[i])
= q + 1 by Corollary 7.
Line 12 is necessary in
KMP-MATCHER
to avoid a possible reference to P[m + 1] on line 6 after an
occurrence of P has been found. (The argument that q = ![]() (Ti -
1) upon the next execution of line 6 remains valid by the hint given in
Exercise 4-6:
(Ti -
1) upon the next execution of line 6 remains valid by the hint given in
Exercise 4-6: ![]() (m, a)
=
(m, a)
=![]() (
(![]() [m], a)
or, equivalently,
[m], a)
or, equivalently, ![]() (Pa)
=
(Pa)
= ![]() (P
(P![]() [m]a) for any a
[m]a) for any a ![]()
![]() .) The
remaining argument for the correctness of the Knuth-Morris-Pratt algorithm
follows from the correctness of FINITE AUTOMATON MATCHER,
since we now see that KMP-MATCHER simulates the behavior of FINITE AUTOMATON MATCHER
.) The
remaining argument for the correctness of the Knuth-Morris-Pratt algorithm
follows from the correctness of FINITE AUTOMATON MATCHER,
since we now see that KMP-MATCHER simulates the behavior of FINITE AUTOMATON MATCHER
Compute the prefix
function ![]() for the
pattern ababbabbababbababbabb when the alphabet is
for the
pattern ababbabbababbababbabb when the alphabet is ![]() = .
= .
Give an upper bound on
the size of ![]() *[q]
as a function of q. Give an example to show that your bound is tight.
*[q]
as a function of q. Give an example to show that your bound is tight.
Explain how to determine
the occurrences of pattern P in the text T by examining the ![]() function for
the string PT (the string of length m + n that is the concatenation
of P and T).
function for
the string PT (the string of length m + n that is the concatenation
of P and T).
Show how to improve KMP-MATCHER by replacing the
occurrence of ![]() in line 7
(but not line 12) by
in line 7
(but not line 12) by ![]() ',
where
',
where ![]() ' is
defined recursively for q = 1, 2, . . . , m by the equation
' is
defined recursively for q = 1, 2, . . . , m by the equation
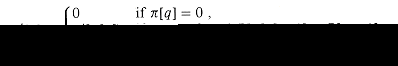
Explain why the modified algorithm is correct, and explain in what sense this modification constitutes an improvement.
Give a linear-time algorithm to determine if a text T is a cyclic rotation of another string T'. For example, arc and car are cyclic rotations of each other.
If the pattern P is relatively long and the
alphabet ![]() is
reasonably large, then an algorithm due to Robert S. Boyer and J. Strother
Moore is likely to be the most efficient string-matching algorithm.
is
reasonably large, then an algorithm due to Robert S. Boyer and J. Strother
Moore is likely to be the most efficient string-matching algorithm.
Aside from the
mysterious-looking ![]() 's and
's and ![]() 's, this
program looks remarkably like the naive string-matching algorithm. Indeed,
suppose we comment out lines 3-4 and replace the updating of s on lines
12-13 with simple incrementations as follows:
's, this
program looks remarkably like the naive string-matching algorithm. Indeed,
suppose we comment out lines 3-4 and replace the updating of s on lines
12-13 with simple incrementations as follows:
The modified program now acts exactly like the naive string matcher: the while loop beginning on line 6 considers each of the n - m + 1 possible shifts s in turn, and the while loop beginning on line 8 tests the condition P[1 . . m] = T[s + 1 . . s + m] by comparing P[j] with T[s + j] for j = m, m - 1, . . . , 1. If the loop terminates with j = 0, a valid shift s has been found, and line 11 prints out the value of s. At this level, the only remarkable features of the Boyer-Moore algorithm are that it compares the pattern against the text from right to left and that it increases the shift s on lines 12-13 by a value that is not necessarily 1.
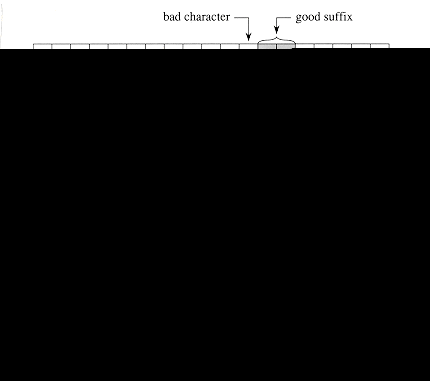
The Boyer-Moore algorithm
incorporates two heuristics that allow it to avoid much of the work that our
previous string-matching algorithms performed. These heuristics are so
effective that they often allow the algorithm to skip altogether the
examination of many text characters. These heuristics, known as the
'bad-character heuristic' and the 'good-suffix heuristic,'
are illustrated in Figure 11. They can be viewed as operating independently in
parallel. When a mismatch occurs, each heuristic proposes an amount by which s
can safely be increased without missing a valid shift. The Boyer-Moore
algorithm chooses the larger amount and increases s by that amount: when
line 13 is reached after a mismatch, the bad-character heuristic proposes
increasing s by j - ![]() [T[s
+ j]], and the good-suffix heuristic proposes increasing s by
[T[s
+ j]], and the good-suffix heuristic proposes increasing s by ![]() [j].
[j].
When a mismatch occurs, the bad-character
heuristic uses information about where the bad text character T[s
+ j] occurs in the pattern (if it occurs at all) to propose a new shift.
In the best case, the mismatch occurs on the first comparison (P[m]
![]() T[s
+ m]) and the bad character T[s + m] does not occur
in the pattern at all. (Imagine searching for am in the text string bn.) In this case, we can increase the shift s by m, since
any shift smaller than s + m will align some pattern character
against the bad character, causing a mismatch. If the best case occurs
repeatedly, the Boyer-Moore algorithm examines only a fraction 1/m of
the text characters, since each text character examined yields a mismatch, thus
causing s to increase by m. This best-case behavior illustrates
the power of matching right-to-left instead of left-to-right.
T[s
+ m]) and the bad character T[s + m] does not occur
in the pattern at all. (Imagine searching for am in the text string bn.) In this case, we can increase the shift s by m, since
any shift smaller than s + m will align some pattern character
against the bad character, causing a mismatch. If the best case occurs
repeatedly, the Boyer-Moore algorithm examines only a fraction 1/m of
the text characters, since each text character examined yields a mismatch, thus
causing s to increase by m. This best-case behavior illustrates
the power of matching right-to-left instead of left-to-right.
In general, the bad-character
heuristic works as follows. Suppose we have just found a mismatch: P[j]
![]() T[s
+ j] for some j, where 1
T[s
+ j] for some j, where 1 ![]() j
j ![]() m. We
then let k be the largest index in the range 1
m. We
then let k be the largest index in the range 1 ![]() k
k ![]() m
such that T[s + j] = P[k], if any such k
exists. Otherwise, we let k = 0. We claim that we may safely increase s
by j - k. We must consider three cases to prove this claim, as
illustrated by Figure 12.
m
such that T[s + j] = P[k], if any such k
exists. Otherwise, we let k = 0. We claim that we may safely increase s
by j - k. We must consider three cases to prove this claim, as
illustrated by Figure 12.
![]() k =
0: As shown in Figure 12(a), the bad character T[s + j]
didn't occur in the pattern at all, and so we can safely increase s by j
without missing any valid shifts.
k =
0: As shown in Figure 12(a), the bad character T[s + j]
didn't occur in the pattern at all, and so we can safely increase s by j
without missing any valid shifts.
![]() k
< j: As shown in Figure 12(b), the rightmost occurrence of the bad
character is in the pattern to the left of position j, so that j
- k > 0 and the pattern must be moved j - k characters to the
right before the bad text character matches any pattern character. Therefore,
we can safely increase s by j - k without missing any valid
shifts.
k
< j: As shown in Figure 12(b), the rightmost occurrence of the bad
character is in the pattern to the left of position j, so that j
- k > 0 and the pattern must be moved j - k characters to the
right before the bad text character matches any pattern character. Therefore,
we can safely increase s by j - k without missing any valid
shifts.
![]() k
> j: As shown in Figure 12(c), j - k < 0, and so the
bad-character heuristic is essentially proposing to decrease s. This
recommendation will be ignored by the Boyer-Moore algorithm, since the
good-suffix heuristic will propose a shift to the right in all cases.
k
> j: As shown in Figure 12(c), j - k < 0, and so the
bad-character heuristic is essentially proposing to decrease s. This
recommendation will be ignored by the Boyer-Moore algorithm, since the
good-suffix heuristic will propose a shift to the right in all cases.
The following simple program defines ![]() [a]
to be the index of the rightmost position in the pattern at which character a
occurs, for each a
[a]
to be the index of the rightmost position in the pattern at which character a
occurs, for each a ![]()
![]() . If a
does not occur in the pattern, then
. If a
does not occur in the pattern, then ![]() [a]
is set to 0. We call
[a]
is set to 0. We call ![]() the last-occurrence
function for the pattern. With this definition, the expression j
-
the last-occurrence
function for the pattern. With this definition, the expression j
- ![]() [T[s
+ j]] on line 13 of BOYER MOORE MATCHER implements the
bad-character heuristic. (Since j -
[T[s
+ j]] on line 13 of BOYER MOORE MATCHER implements the
bad-character heuristic. (Since j - ![]() [T[s
+ j]] is negative if the rightmost occurrence of the bad character T[s
+ j] in the pattern is to the right of position j, we rely on the
positivity of
[T[s
+ j]] is negative if the rightmost occurrence of the bad character T[s
+ j] in the pattern is to the right of position j, we rely on the
positivity of ![]() [j],
proposed by the good-suffix heuristic, to ensure that the algorithm makes
progress at each step.)
[j],
proposed by the good-suffix heuristic, to ensure that the algorithm makes
progress at each step.)

The running time of
procedure COMPUTE LAST OCCURRENCE FUNCTION is O(|![]() | + m).
| + m).
Let us define the relation Q ~
R (read 'Q is similar to R') for strings Q and
R to mean that ![]() . If two
strings are similar, then we can align them with their rightmost characters
matched, and no pair of aligned characters will disagree. The relation
'~' is symmetric: Q ~ R if and only if R ~ Q.
We also have, as a consequence of Lemma 1, that
. If two
strings are similar, then we can align them with their rightmost characters
matched, and no pair of aligned characters will disagree. The relation
'~' is symmetric: Q ~ R if and only if R ~ Q.
We also have, as a consequence of Lemma 1, that
![]()
If we find that P[j]
![]() T[s
+ j], where j < m, then the good-suffix heuristic
says that we can safely advance s by
T[s
+ j], where j < m, then the good-suffix heuristic
says that we can safely advance s by
We now show how to
compute the good-suffix function ![]() . We first
observe that
. We first
observe that ![]() [j]
[j] ![]() m -
m - ![]() [m]
for all j, as follows. If w =
[m]
for all j, as follows. If w = ![]() [m],
then
[m],
then ![]() by the
definition of
by the
definition of ![]() .
Furthermore, since
.
Furthermore, since ![]() for any j,
we have Pw ~ P[j + 1 . . m], by equation
(7). Therefore,
for any j,
we have Pw ~ P[j + 1 . . m], by equation
(7). Therefore, ![]() [j]
[j] ![]() m -
m - ![]() [m]
for all j.
[m]
for all j.
We can now rewrite our
definition of ![]() as
as
The condition that P[j
+ 1 . . m] ~ Pk holds if either 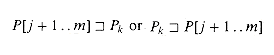 . But the
latter possibility implies that
. But the
latter possibility implies that ![]() and thus
that k
and thus
that k ![]()
![]() [m],
by the definition of
[m],
by the definition of ![]() . This
latter possibility cannot reduce the value of
. This
latter possibility cannot reduce the value of ![]() [j]
below m -
[j]
below m - ![]() [m].
We can therefore rewrite our definition of
[m].
We can therefore rewrite our definition of ![]() still
further as follows:
still
further as follows:
![]()
(The second set may be
empty.) It is worth observing that the definition implies that ![]() [j]
> 0 for all j = 1, 2, . . . , m, which ensures that the
Boyer-Moore algorithm makes progress.
[j]
> 0 for all j = 1, 2, . . . , m, which ensures that the
Boyer-Moore algorithm makes progress.
To simplify the
expression for ![]() further, we
define P' as the reverse of the pattern P and
further, we
define P' as the reverse of the pattern P and ![]() ' as the
corresponding prefix function. That is P'[i] = P[m
- i + 1] for i = 1, 2, . . . , m, and
' as the
corresponding prefix function. That is P'[i] = P[m
- i + 1] for i = 1, 2, . . . , m, and ![]() '[t]
is the largest u such that u < t and
'[t]
is the largest u such that u < t and ![]() .
.
If k is the
largest possible value such that ![]() , then we
claim that
, then we
claim that
where l = (m -
k) + (m - j). To see that this claim is well defined, note that ![]() implies that
m - j
implies that
m - j ![]() k,
and thus l
k,
and thus l ![]() m.
Also, j < m and k
m.
Also, j < m and k ![]() m, so
that l
m, so
that l ![]() 1. We prove
this claim as follows. Since
1. We prove
this claim as follows. Since ![]() . Therefore,
. Therefore,
![]() '[l]
'[l] ![]() m - j.
Suppose now that p > m - j, where p =
m - j.
Suppose now that p > m - j, where p = ![]() '[l].
Then, by the definition of
'[l].
Then, by the definition of ![]() ', we have
', we have ![]() or,
equivalently, P'[1 . . p] = P'[l - p + 1 .
. l]. Rewriting this equation in terms of P rather than P',
we have P[m - p + 1 . . m] = P[m - l + 1 .
. m - l + p]. Substituting for l = 2m - k - j, we obtain P[m
- p + 1 . . m] = P[k - m + j + 1 . . k - m + j +p],
which implies
or,
equivalently, P'[1 . . p] = P'[l - p + 1 .
. l]. Rewriting this equation in terms of P rather than P',
we have P[m - p + 1 . . m] = P[m - l + 1 .
. m - l + p]. Substituting for l = 2m - k - j, we obtain P[m
- p + 1 . . m] = P[k - m + j + 1 . . k - m + j +p],
which implies ![]() . Since p
> m - j, we have j + 1 > m-p+1, and so
. Since p
> m - j, we have j + 1 > m-p+1, and so ![]() , implying
that
, implying
that ![]() by the
transitivity of
by the
transitivity of ![]() . Finally,
since p > m - j, we have k' > k, where k' = k - m + j +
p, contradicting our choice of k as the largest possible value such
that
. Finally,
since p > m - j, we have k' > k, where k' = k - m + j +
p, contradicting our choice of k as the largest possible value such
that ![]() . This
contradiction means that we can't have p > m - j, and hus = m - j,
which proves the claim (8).
. This
contradiction means that we can't have p > m - j, and hus = m - j,
which proves the claim (8).
Using equation (8), and
noting that ![]() '[l]
= m - j implies that j = m -
'[l]
= m - j implies that j = m - ![]() '[l]
and k = m - l +
'[l]
and k = m - l + ![]() '[l],
we can rewrite our definition of
'[l],
we can rewrite our definition of ![]() still
further:
still
further:
Again, the second set may be empty.
We are now ready to
examine the procedure for computing ![]() .
.
The procedure COMPUTE GOOD SUFFIX FUNCTION is a straightforward implementation of equation (9). Its running time is O(m).
The worst-case running
time of the Boyer-Moore algorithm is clearly O((n - m +1)m
+ |![]() |), since COMPUTE LAST OCCURRENCE FUNCTION takes time O(m
+ |
|), since COMPUTE LAST OCCURRENCE FUNCTION takes time O(m
+ |![]() |), COMPUTE GOOD SUFFIX FUNCTION takes time O(m),
and the Boyer-Moore algorithm (like the Rabin-Karp algorithm) spends O(m)
time validating each valid shift s. In practice, however, the
Boyer-Moore algorithm is often the algorithm of choice.
|), COMPUTE GOOD SUFFIX FUNCTION takes time O(m),
and the Boyer-Moore algorithm (like the Rabin-Karp algorithm) spends O(m)
time validating each valid shift s. In practice, however, the
Boyer-Moore algorithm is often the algorithm of choice.
Compute the ![]() and
and ![]() functions
for the pattern P = and the alphabet
functions
for the pattern P = and the alphabet ![]() = .
= .
Give examples to show that by combining the bad-character and good-suffix heuristics, the Boyer-Moore algorithm can perform much better than if it used just the good-suffix heuristic.
An improvement to the
basic Boyer-Moore procedure that is often used in practice is to replace the ![]() function by
function by ![]() ', defined
by
', defined
by
In addition to ensuring
that the characters in the good suffix will be mis-matched at the new shift,
the ![]() ' function
also guarantees that the same pattern character will not be matched up against
the bad text character. Show how to compute the
' function
also guarantees that the same pattern character will not be matched up against
the bad text character. Show how to compute the ![]() ' function
efficiently.
' function
efficiently.
34-1 String matching based on repetition factors
Let yi denote the concatenation of
string y with itself i times. For example, (ab ababab. We say that a string x
![]()
![]() *
has repetition factor r if x = yr for
some string y
*
has repetition factor r if x = yr for
some string y ![]()
![]() *
and some r > 0. Let p(x) denote the largest r
such that x has repetition factor r.
*
and some r > 0. Let p(x) denote the largest r
such that x has repetition factor r.
a Give an efficient algorithm that takes as
input a pattern P[1 . . m] and computes ![]() (Pi)
for i = 1, 2, . . . , m. What is the running time of
your algorithm?
(Pi)
for i = 1, 2, . . . , m. What is the running time of
your algorithm?
b. For any pattern P[1 . . m], let p*(P) be
defined as max1![]() i
i![]() m
m
![]() (Pi).
Prove that if the pattern P is chosen randomly from the set of all
binary strings of length m, then the expected value of
(Pi).
Prove that if the pattern P is chosen randomly from the set of all
binary strings of length m, then the expected value of ![]() *(P)
is O(1).
*(P)
is O(1).
c. Argue that the following string-matching algorithm correctly finds
all occurrences of pattern P in a text T[1 . . n] in time O(![]() *(P)n
+ m).
*(P)n
+ m).
This algorithm is due to Galil and Seiferas. By extending these ideas greatly, they obtain a linear-time string-matching algorithm that uses only O(1) storage beyond what is required for P and T.
34-2 Parallel string matching
Consider the problem of
string matching on a parallel computer. Assume that for a given pattern, we
have a string-matching automaton M with state set Q. Let ![]() be the
final-state function for M. Suppose that our input ext is T[1 . .
n]. We wish to compute
be the
final-state function for M. Suppose that our input ext is T[1 . .
n]. We wish to compute ![]() (Ti)
for i = 1, 2, . . . , n; that is, we wish to compute the final
state for each refix. Our strategy is to use the parallel prefix computation
described in Section 30.1.2.
(Ti)
for i = 1, 2, . . . , n; that is, we wish to compute the final
state for each refix. Our strategy is to use the parallel prefix computation
described in Section 30.1.2.
For any input string x,
define the function ![]() x
: Q
x
: Q ![]() Q
such that if M starts in state q and reads input x, then M
ends in state
Q
such that if M starts in state q and reads input x, then M
ends in state ![]() x(q).
x(q).
a. Prove that ![]() denotes
functional composition:
denotes
functional composition:
![]()
b. Argue that ![]() is an
associative operation.
is an
associative operation.
c.
Argue that ![]() xy
can be computed from tabular representations of
xy
can be computed from tabular representations of ![]() x and
x and
![]() y
in O(1) time on a CREW PRAM. Analyze how many processors are needed in
terms of |Q|.'
y
in O(1) time on a CREW PRAM. Analyze how many processors are needed in
terms of |Q|.'
d. Prove that ![]() (Ti)
=
(Ti)
= ![]() Ti(q0),
where q0 is the start state for M.
Ti(q0),
where q0 is the start state for M.
e. Show how to find all occurrences of a pattern in a text of length n in O(lg n ) time on a CREW PRAM. Assume that the pattern is supplied in the form of the corresponding string-matching automaton.
The relation of string matching to the theory of finite automata is discussed by Aho, Hopcroft, and Ullman [4]. The Knuth-Morris-Pratt algorithm [125] was invented independently by Knuth and Pratt and by Morris; they published their work jointly. The Rabin-Karp algorithm was proposed by Rabin and Karp [117], and the Boyer-Moore algorithm is due to Boyer and Moore [32]. Galil and Seiferas [78] give an interesting deterministic linear-time string-matching algorithm that uses only O(1) space beyond that required to store the pattern and text.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3443
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved