| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Boundary Layer Similarity
![]()
![]()
 ≈0
≈0
![]()

![]()
≈0
![]()
![]() For
low-speed, forced convection flows :
For
low-speed, forced convection flows : 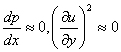
RHS = diffusion terms
LHS = convection terms
The last three equations are very similar
B.L. Similarity Parameters: Re, Pr, Sc
![]() L
- is some characteristic length
L
- is some characteristic length
![]() U∞
- is the free stream velocity
U∞
- is the free stream velocity
![]() T∞
- is the free stream temperature
T∞
- is the free stream temperature
TS - is the surface temperature
![]() CA,S
is the concentration of species A at the surface
CA,S
is the concentration of species A at the surface
CA,∞ - is the concentration of species A free stream
![]()
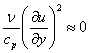
Using the above dimensionless independent variables, the B.L. equations become:
![]()
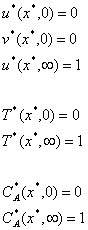
![]()
![]()
![]()
≈0
![]()
Reynolds #: ![]()
Prandtl #: ![]() Pr≈1
for gases
Pr≈1
for gases
Pr>>1 for oils
Pr<<1 for liquid metane
Schmidth #: ![]()
Lewis #: ![]()
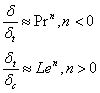
Other dimensionless groups:
Biot #: ![]()
Nusselt #: ![]()
![]()
Sherwood #: ![]()
Mass Transfer
![]()
Functional Form of the solutions for the B.L. Equations
![]() Eq.
2 :
Eq.
2 : ![]()
≈ on the geometry of the surface
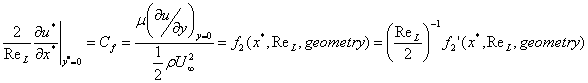
universally applicable to different fluids and over a wide range of values for U∞ and L
Eq. 3 :

Eq. 4:
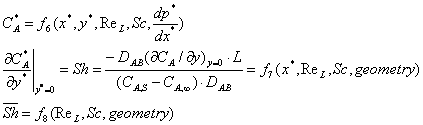
The similarity parameters reduce the independent variables and make the solutions universally applicable
Boundary Layer Analogies
The Heat and Mass Transfer Analogy
Eq. (3) and (4), as well as the associated boundary conditions are analogous → T* and C*A must be of the same functional form
└→ heat and mass transfer relations for a particular geometry are interchangeable
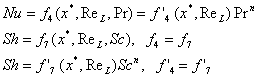
![]()
Hence, h can be obtained from knowledge of hm and vice-versa.
![]() The
same relation can be applied to
The
same relation can be applied to ![]() and
and ![]() ,
and it may be used in turbulent, as well as laminar flow.
,
and it may be used in turbulent, as well as laminar flow.

![]()
Example
T∞=200C
![]() V=100
m/s TS=800C
V=100
m/s TS=800C
P=1 at

![]()
![]()
![]()
![]() L=1m
L=1m
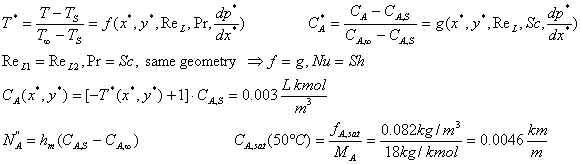
If ![]() and Sc=Pr => Eqs. (2)-(4) are of precisely the same form
and Sc=Pr => Eqs. (2)-(4) are of precisely the same form
u*,T* and CA* are equivalent as solutions.
![]()


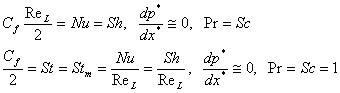
Reynolds analogy
It has been shown that, with certain corrections, the analogy may be applied over a wide range of Pr and Sc.

![]()
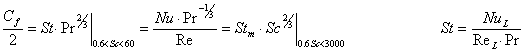
modified Reynolds or Chilton-Colburn analogies
!!! also valid for averages: ![]()
End Note:
PROBLEM 1.
KNOWN: Air flow conditions and drag force associated with a heater of prescribed surface temperature and area,
FIND: Required heater power.
SCHEMATIC:


ASSUMPTIONS: (1) Steady-state conditions, (2) Reynolds analogy is applicable, (3) Bottom surface is adiabatic.
PROPERTIES: Air (Tf=350K, 1 at): ρ=0.995 kg/m3, cp=1009 J/Kg K, Pr=0.7
ANALYSIS: The average shear stress and friction coefficient are
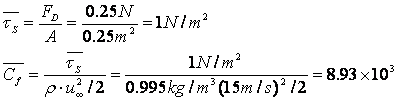
From the Reynolds analogy, modified:
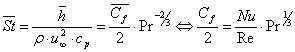
Solving for ![]() and substituting numerical values, find
and substituting numerical values, find
![]() =0.995
kg/m3(15 m/s) 1009 J/kg K (8.93x10-3/2)(0.7)-2/3 ;
=0.995
kg/m3(15 m/s) 1009 J/kg K (8.93x10-3/2)(0.7)-2/3 ;
![]() =85
W/m2K
=85
W/m2K
Hence, the heat rate is :
q=![]() A(TS-T )=85W/m2K(0.25m2)(140-15)oC;
A(TS-T )=85W/m2K(0.25m2)(140-15)oC;
q=2.66kW
COMMENTS: Due to bottom heat losses, which have been assumed negligible, the actual power requirement would exceed 2.66kW.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1312
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved