| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
AFFINE SPACES
The most of the geometrical notions of this chapter will be studied in spaces for which the notions of point and vector are indispensable. The notion of affine space allows using the two notions in a well-defined environment.
1. Definition and Examples
Lets consider the non-empty set A = and agree to name each of its elements points, and bipoint of A any element (A, B) I A A . Point A will be named the origin of the bipoint (A, B). Bipoints (A, B) and (B, A) will be named symmetric bipoints.
|
1.1 Definition |
It is called affine space the triplet A, V, j), where
A is a non-empty set of points, V an K-vector space, and the function j A A A, B, C I A j (A, B) + j (B, C) = j (A, C) A |
The set A is named support set of the affine space, and its elements will be named points of the affine space. The vector space V is named the directorial vector space of the affine space, and its elements will be named vectors of the affine space. The function j is named the affine structure function.
The elements of an affine space are points and vectors.
The affine space (A, V, j) is named real or complex by the vector space V which can be real or complex.
If we consider A = B
= C in the axiom A1) , then j (A, A) =![]() , A I A. Therefore, thru the structure
function, to any bipoint (A, A)
corresponds the null vector
, A I A. Therefore, thru the structure
function, to any bipoint (A, A)
corresponds the null vector![]() .
.
The corresponding vectors of a pair of symmetrical bipoints are opposite vectors. Indeed, if we consider C = B, in axiom A1), we have
j (A, B) = - j (B, A).
|
1.2 Consequence. |
Function j is surjective and moreover, for each fixed point O I A jO A V , jO (A) = j (O, A), A I A, is bijective. |
The proof followes considering axioms A1) and A2).
In an affine space (A, V, j), the function j determines an equivalence relation on the bipoints set of A, which we will name relation of equipollence.
We will say that the bipoint (A, B) is equipollent with the bipoint (C, D) if they have the same image thru j
(A, B) ~ (C, D) ![]() j (A, B) = j (C, D) (1.1)
j (A, B) = j (C, D) (1.1)
It is easy to verify that the relation ~ is reflexive, symmetric and transitive, meaning it is a relation of equipollence over A A.
The factor space A
A is in a bijective correspondence with the
vector space V. To each vector ![]()
![]() V, corresponds a
single equivalence class of equipollent bipoints, and that is:
V, corresponds a
single equivalence class of equipollent bipoints, and that is:
(![]() ) = (1.2)
) = (1.2)
When we identify the factor space A
A with the vector space V
thru this bijection, the class of the bipoint (A, B) denoted by ![]() , is named free vector
of the affine space.
, is named free vector
of the affine space.
Considering this, the axioms A1) and A2) can be written as follows:
A, B, C I A ![]() (1.3)
(1.3)
![]() A,
A,![]() BI A unique such that
BI A unique such that ![]()
Let O IA be a fixed point and A A = the set of the bipoints with O as origin.
Taking into consideration the
Consequence 1.2 and that the relation A
I A ![]() (O, A)IA is a bijective correspondence, it
results that A can identify itself as well with A as with the directorial vector
space V.
(O, A)IA is a bijective correspondence, it
results that A can identify itself as well with A as with the directorial vector
space V.
When A is identified with the vector
space V, a vector structure from V is induced on A. The vectors of this space are
called tied vectors of the affine
space, or tangent vectors in O to A, and will be denoted by ![]() .
.
When A is identified with the vector space A thru the bijection A I A (O, A) I Ao, it means that A was considered a vector space having as origin the point O.
The vector ![]() will be named position vector.
will be named position vector.
Actually in any point O I A of an affine space (A V j), a vector space A, which identifies with A, can be constructed.
Following these identifications, the notion of dimension of an affine space is justified as being the dimension of the directorial vector space V.
If dimV= n, then the affine space of dimension n will be denoted by (A n, Vn), shortly A n
If the vector space V is an euclidean vector space, then the affine space (A, V, j) is called euclidean punctual space. If dimV=n, then we will denote by En the corresponding euclidean vector space. The euclidean structure of the directorial vector space V will allow studying the metric properties of certain subsets of the euclidean punctual space En
There are affine spaces that are not vector
spaces. But, any vector space is an affine space, because the function j: V V
V,
![]() verifies the axioms A1)
and A2). The affine space (V, V, j) such defined is named canonical affine space associated to the vector space V.
verifies the axioms A1)
and A2). The affine space (V, V, j) such defined is named canonical affine space associated to the vector space V.
1 The standard affine space
Lets consider the standard space Kn. This space can be organized as a vector space for which we can associate the canonical affine space (Kn, Kn, j ), where the affine structure function j is defined by the relation j ( A, B) = ( b1 - a1, b2 - a2 , , bn - an ) , for A = ( a1, a2 , , an ) and B = (b1, b2, , bn). This affine space is named standard affine space and will be denoted with Kn as well.
Particularly for K = R, we have the affine standard space (Rn, Rn, j) where the directorial vector space Rn is an euclidean space, therefore the affine space (Rn, Rn, j) becomes an euclidean punctual space.
2 The geometrical affine space of the free vectors
Lets consider as, support set, the
punctual space of the elementary geometry, denoted by E , as directorial vector space , the vector space of the free vectors V and as
affine structure function j : E3 E3
V j(A,B) =![]()
![]() V
V
In this way we obtain the geometrical affine space of the free vectors A = (E3, V j). This space constituted the model for the affine spaces. We will study in detail this space in the next chapter.
3 The linear variety of a vector space V are affine spaces.
A
linear variety of a vector space V is a subset L, ![]() , where V is a vector subspace of V.
, where V is a vector subspace of V.
If we consider the function:
j : L L
V , ![]() ,
,
then the axioms A1) and A2) are satisfied and, therefore, the triplet (L, V j is an affine space.
In particular, any vector subspace is an affine space.
|
2.5 Definition. |
A cartesian frame is a pair R , where O is a fixed point in An, and B is a basis of the directorial vector space. |
Let
B be a basis of the vector space Vn. Then, for
each point P I An, the
position vector ![]() can be written in an
unique way as follows:
can be written in an
unique way as follows:
![]() (2.8)
(2.8)
The
scalars x1, x2,, xn are called cartesian
coordinates of the point P with
respect to frame R , and the bijection ![]() is called function of coordinates with respect to
frame R
is called function of coordinates with respect to
frame R
Let R be a cartesian frame in An . Another frame R of An will be determined in an unique way if we know the position vector of the point O with respect to the initial frame R and the relation between the basis B and the initial basis
B , that is:
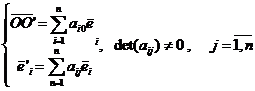 (2.9)
(2.9)
If
P I An is a
point and (xi), (xj), i,j = ![]() are its
coordinates in the frame R respectively R , then from the relation
are its
coordinates in the frame R respectively R , then from the relation ![]() we obtain the
formulas:
we obtain the
formulas:
![]() (2.10)
(2.10)
called the coordinate transformation formula.
By denoting X = t[x1, x2, , xn], X = t[x , x , , x n], A0 = (ai0),
A = (aij) we can write the coordinate transformation formula in the following form:
![]() (2.11)
(2.11)
The matrix ![]() of n + 1 rank is called the matrix of change of frames from R to R
of n + 1 rank is called the matrix of change of frames from R to R
In particular, if B B then A = I and the equations (2.11) are written as:
![]() (2.11)
(2.11)
The changing of the frame R with R governed by the coordinate transformation formula (11) is called translation.
If O = O, then
changing the frame R with the frame R , meaning ai0
= 0, ![]() , is called centro-affinity
and is characterised by the following equations:
, is called centro-affinity
and is characterised by the following equations:
![]() (2.11)
(2.11)
Let (A , V, j) be an affine space, A a non-empty subset of A and j its restriction to A A If V j A A ) is a vector subspace of V then the axioms A1) and A2) are satisfied for the triplet
A , V j
|
3.1 Definition. |
We call affine subspace of the affine space A , V, j a triplet (A , V j ) , with the properties: -A A is a non-empty subset - V j A A ) is a vector subspace of V j is the restriction of j to A A |
An
affine subspace of the affine space (A , V, j) is determined either by the subset A A for which j A A ) = V V is a vector subspace,
or by a point P0 I A and a vector subspace V V. In this case the
support set is given by ![]() .
.
Let
us consider A and ![]() two affine spaces.
two affine spaces.
|
3.7 Definition |
An application t: A t aP bQ at(P) + bt(Q), P, Q I A and a b I K, a b=1 is called an affine application. |
An
affine application t:A ![]() uniquely determines
the morphism T: V
uniquely determines
the morphism T: V ![]() between the associated
vector spaces. Knowing that for
between the associated
vector spaces. Knowing that for ![]() and A I A, B I A such that j (A, B)
=
and A I A, B I A such that j (A, B)
= ![]() , we can define the associated linear map T : V
, we can define the associated linear map T : V
![]() by
by ![]() , where
, where ![]() is affine structure
function of the space
is affine structure
function of the space ![]() . The definition does not depend on the choice of the point
A.
. The definition does not depend on the choice of the point
A.
The set of all bijective affine applications on A represents a group GA(A), called the affine group.
We will name object of the affine space A any subset of points belonging to A
By affine geometry of the affine space A, means the study of all objects, and their invariant properties with respect to the affine group.
The simplest and yet most important affine properties are:
the property collinearity of three points
the property of two affine spaces to be parallel
These mentioned affine properties aid in determining other properties, therefore they will be called fundamental affine properties.
4. The geometrical affine space of the free vectors
Let us consider E3 the punctual space of the elementary geometry and V the vector space of the free vectors.
If
we associate to any bipoint (A, B) I E3
E3
the free vector![]() I V , then the application j : E3 E3
V j (A,
B) =
I V , then the application j : E3 E3
V j (A,
B) = ![]() satisfies properties A1)
and A2) of the affine space definition:
satisfies properties A1)
and A2) of the affine space definition:
A1) A, B, C I E3
, ![]()
A2) ![]() I V A
I E3
exists B I E3
uniquely determined by
I V A
I E3
exists B I E3
uniquely determined by ![]() .
.
|
4.1 Definition. |
The triplet A (E3, V j) is called the affine geometrical space of the free vectors. |
The
elements of the affine space A are
points and vectors. The points of the
affine space A are
points of the support set E3 and
we will denote them by capital letters A,
B, C, , O, P, , and the vectors of the affine
space A are
vectors of the directorial vector space V , free vectors that well denote by ![]() ,
, ![]() , , or by
, , or by ![]() . The application j : E3 E3
V which satisfies axioms A1) and A2)
represents the affine structure function, and the equivalence relation defined
by it on the set E3 is
exactly the relation of equipollence ~ of oriented segments, like it was
defined in the euclidean geometry.
. The application j : E3 E3
V which satisfies axioms A1) and A2)
represents the affine structure function, and the equivalence relation defined
by it on the set E3 is
exactly the relation of equipollence ~ of oriented segments, like it was
defined in the euclidean geometry.
Consider O I E3 a fixed point. The application j : E3 E3 V defined by j (A) = j(O, A), A I E3 is bijective allowing the identification of the punctual space E3 with the vector space of the free vectors.
The
point O I E3,
corresponding to the null vector ![]() , will be considered as origin of the affine space A . Furthermore,
, will be considered as origin of the affine space A . Furthermore, ![]() IV3 there exists an unique point A I E3
determined by the relation
IV3 there exists an unique point A I E3
determined by the relation ![]() . The vector
. The vector ![]() is called the position vector of point A.
is called the position vector of point A.
The set of the position vectors forms an isomorphic vector space with the vector space of the free vectors.
Lets consider now two distinct points A and B of the space E3. The affine subspace generated by A and B, L() = = d is a subspace of dimension one named affine line, shortly - line, having the directorial vector space the vector line
V
For
each point P I d
, collinear with A and B, the system of points is affine-dependent, that means the vectors ![]() and
and ![]() are linearly dependent.
are linearly dependent.
We remind that two vectors with the same direction are named collinear vectors. The vectors of the subspace V have the same direction, which justifies the definition of collinearity from an affine space.
|
4.2 Proposition. |
Two vectors |
Proof. Consider O
I E3
a fixed point. Consider A, B I E3
such that ![]() and
and ![]() . If
. If ![]() ,
, ![]() are collinear then
the points O, A, B are collinear,
meaning that the system of points is affine dependent. This is equivalent with the linear dependence of
the vectors
are collinear then
the points O, A, B are collinear,
meaning that the system of points is affine dependent. This is equivalent with the linear dependence of
the vectors ![]() and
and ![]() .
.
The
oriented segments ![]() and
and ![]() are the representation
of vectors
are the representation
of vectors ![]() and
and ![]() in O, meaning that
in O, meaning that ![]() are
are ![]() linearly dependent
for any choice of point O.
linearly dependent
for any choice of point O.
Conversely,
if ![]() and
and ![]() I V are linearly dependent, then O I E3,
the vectors
I V are linearly dependent, then O I E3,
the vectors ![]() and
and ![]() are linearly
dependent, meaning that the system of points is affine dependent. The collinearity of the points O, A, and B is equivalent with the fact that the vectors
are linearly
dependent, meaning that the system of points is affine dependent. The collinearity of the points O, A, and B is equivalent with the fact that the vectors ![]() and
and ![]() have the same
direction. (q.e.d.)
have the same
direction. (q.e.d.)
If
![]() is collinear with
is collinear with ![]() then we write:
then we write:
![]() , l I R (the condition of
collinearity) (4.1)
, l I R (the condition of
collinearity) (4.1)
|
4.3 Consequence. |
The subset
|
Any three non-collinear points are affine dependent, meaning that any two non-collinear vectors are linearly dependent.
Three non-collinear points A, B, C I E3 determine a plane. The plane generated by these three affine independent points is determined by:
A p
affine subspace having as directorial vector space the vector plane:
![]()
For
any point PI p , the system is affine dependent, which means that the vectors ![]() ,
, ![]() and
and ![]() are linearly
dependent.
are linearly
dependent.
Three
vectors ![]() ,
, ![]() and
and ![]() are considered to be
coplanar if they are parallel with a plane.
are considered to be
coplanar if they are parallel with a plane.
|
4.4 Proposition. |
Three vectors l m n I R, l m n such that |
If ![]() ,
, ![]() I V are two vectors, then
I V are two vectors, then ![]() I V coplanar with
I V coplanar with ![]() and
and ![]() , can be written as follows:
, can be written as follows:
![]() =
= ![]() , l m I R , (the condition of coplanarity) (4.2)
, l m I R , (the condition of coplanarity) (4.2)
|
4.5 Consequence. |
The subset
|
Consider now four non-coplanar points A, B, C, D I E3 . The system of points is affine independent, which means that any three non-coplanar vectors are linearly independent. The affine space generated by four non-coplanar points is of dimension three and any five points of this space will be affine dependent.
|
4.6 Theorem. |
The vector space V has three dimensions. |

Proof. Any four non-coplanar points form an
independent affine system, which is equivalent with the existence of three
non-coplanar (linearly independent) vectors ![]() ,
,![]() ,
,![]() . Let us demonstrate that these three non-coplanar vectors
generate the vector space of the free vectors V . For this, let
. Let us demonstrate that these three non-coplanar vectors
generate the vector space of the free vectors V . For this, let ![]() be a fourth vector, O I E3
some point, and
be a fourth vector, O I E3
some point, and ![]() ,
, ![]() ,
, ![]() ,
, ![]() the
the
Fig. 1
representatives of the vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() in the point O (fig. 1).
in the point O (fig. 1).
Using twice the parallelogram rule for summing two free vectors in the parallelogram OA1X1B and respectively OX1XC1, it results:
![]()
Because ![]() and
and ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and ![]() are collinear then we
have
are collinear then we
have
![]() or
or
![]() ,
,
namely is a basis for the vector space of the free vectors, therefore dimV = 3. q.e.d.
For
any point O I E3
and a given basis in V , the
ensemble R (O; ![]() ) represents a
cartesian frame in the affine space A ( E3, V j
) represents a
cartesian frame in the affine space A ( E3, V j
For
any point P I E3
we have the position vector ![]() given by:
given by:
![]() ; x1,
x2, x3 I R
; x1,
x2, x3 I R
The scalars x1, x2, x3 I R are called cartesian coordinates of point P.
If ![]() I V is a free vector, then P I E3
is unique, such that
I V is a free vector, then P I E3
is unique, such that ![]() , and in the frame R
, and in the frame R ![]() is written as:
is written as:
![]() ,
,
where the scalars x1, x2,
x3 I R, the coordinates of point P, will be called the coordinates of
vector ![]() in the frame R
in the frame R
If
R(O; ![]() ) is a fixed cartesian frame, A is a geometrical affine space and x1, x2, x3
I R are the coordinates of vector
) is a fixed cartesian frame, A is a geometrical affine space and x1, x2, x3
I R are the coordinates of vector ![]() I V , we will write that
I V , we will write that ![]() = ( x1, x2, x3)
or briefly
= ( x1, x2, x3)
or briefly ![]() ( x1, x2, x3).
( x1, x2, x3).
If
we have ![]() ( x1, x2,
x3) and
( x1, x2,
x3) and ![]() ( y1, y2,
y3) two free vectors,
then:
( y1, y2,
y3) two free vectors,
then:
1
![]() is collinear with
is collinear with ![]() (
(![]() ||
||![]() ) if and only if their coordinates are proportional (or equal
in the particular case of
) if and only if their coordinates are proportional (or equal
in the particular case of ![]() =
= ![]() ).
).
2
![]() ,
, ![]() ,
, ![]() are coplanar if and
only if the coodinates of one vector represents a linear combination of the
other two.
are coplanar if and
only if the coodinates of one vector represents a linear combination of the
other two.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2869
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved