| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The Reality of Causes in a World of Instrumental Laws
0. Introduction
Empiricists are notoriously suspicious of causes. They have not been equally wary of laws. Hume set the tradition when he replaced causal facts with facts about generalizations. Modern empiricists do the same. But nowadays Hume's generalizations are the laws and equations of high level scientific theories. On current accounts, there may be some question about where the laws of our fundamental theories get their necessity; but it is no question that these laws are the core of modern science. Bertrand Russell is well known for this view:
The law of gravitation will illustrate what occurs in any exact science . . . Certain differential equations can be found, which hold at every instant for every particle of the system . . . But there is nothing that could be properly called cause and nothing that could be properly called effect in such a system.1
For Russell, causes though useful to daily life and in the infancy of a science, tend to be displaced by quite different laws as soon as a science is successful.
It is convenient that Russell talks about physics, and that
the laws he praises are its fundamental equations
end p.74
Explaining by Causes
Following Bromberger, Scriven, and others, we know that
there are various things one can be doing in explaining. Two are of importance
here: in explaining a phenomenon one can cite the causes of that phenomenon; or
one can set the phenomenon in a general theoretical framework. The framework of
modern physics is mathematical, and good explanations will generally allow us
to make quite precise calculations about the phenomena we explain. Rene Thom
remarks the difference between these two kinds of explanation, though he thinks
that only the causes really explain: DesCartes with his vortices, his hooked
atoms, and the like explained everything and calculated nothing;
Unlike Thom, I am happy to call both explanation, so long as
we do not illicitly attribute to theoretical explanation features that apply
only to causal explanation. There is a tradition, since the time of Aristotle,
of deliberately conflating the two. But I shall argue that they function quite
differently in modern physics. If we accept Descartes's causal story as
adequate, we must count his claims about hooked atoms and vortices true. But we
do not use
One powerful argument speaks against my claim and for the truth of explanatory lawsthe argument from coincidence. Those who take laws seriously tend to subscribe to what Gilbert Harman has called inference to the best explanation. They assume that the fact that a law explains provides evidence that the law is true. The more diverse the phenomena that it explains, the more likely it is to be true. It would be an absurd coincidence if a wide variety of different kinds of phenomena were all explained by a particular law, and yet were not in reality consequent from the law. Thus the argument from coincidence supports a good many of the inferences we make to best explanations.
The method of inference to the best explanation is subject to an important constraint, howeverthe requirement of non-redundancy. We can infer the truth of an explanation only if there are no alternatives that account in an equally satisfactory way for the phenomena. In physics nowadays, I shall argue, an acceptable causal story is supposed to satisfy this requirement. But exactly the opposite is the case with the specific equations and models that make up our theoretical explanations. There is redundancy of theoretical treatment, but not of causal account.
There is, I think, a simple reason for this: causes make their effects happen. We begin with a phenomenon which, relative to our other general beliefs, we think would not occur unless something peculiar brought it about. In physics we often mark this belief by labelling the phenomena as effectsthe Sorbet effect, the Zeeman effect, the Hall effect. An effect needs something to bring it about, and the peculiar features of the effect depend on the particular nature of the cause, so thatin so far as we think we have got it rightwe are entitled to infer the character of the cause from the character of the effect.
But equations do not bring about the phenomenological laws we derive from them (even if the phenomenological laws are themselves equations). Nor are they used in physics as if they did. The specific equations we use to treat particular phenomena provide a way of casting the phenomena into the general framework of the theory. Thus we are able to treat a variety of disparate phenomena in a similar way, and to make use of the theory to make quite precise calculations. For both of these purposes it is an advantage to multiply theoretical treatments.
Pierre Duhem used the redundancy requirement as an argument against scientific realism, and recently Hilary Putman uses it as an argument against realism in general. Both propose that, in principle, for any explanation of any amount of data there will always be an equally satisfactory alternative. The history of science suggests that this claim may be right: we constantly construct better explanations to replace those of the past. But such arguments are irrelevant here; they do not distinguish between causal claims and theoretical accounts. Both are likely to be replaced by better accounts in the future.
end p.76
Here I am not concerned with alternatives that are at best available only in principle, but rather with the practical availability of alternatives within theories we actually have to hand. For this discussion, I want to take the point of view that Putnam calls internal realism; to consider actual physical theories which we are willing to account as acceptable, even if only for the time being, and to ask, Relative to that theory, which of its explanatory claims are we to deem true? My answer is that causal claims are to be deemed true, but to count the basic explanatory laws as true is to fail to take seriously how physics succeeds in giving explanations.
I will use two examples to show this. The firstquantum damping and its associated line broadeningis a phenomenon whose understanding is critical to the theory of lasers. Here we have a single causal story, but a fruitful multiplication of successful theoretical accounts. This contrasts with the unacceptable multiplication of causal stories in the second example.
There is one question we should consider before looking at the examples, a question pressed by two colleagues in philosophy of science, Dan Hausman and Robert Ennis. How are we to distinguish the explanatory laws, which I argue are not to be taken literally, from the causal claims and more pedestrian statements of fact, which are? The short answer is that there is no way. A typical way of treating a problem like this is to find some independent criterionideally syntactical, but more realistically semanticalwhich will divide the claims of a theory into two parts. Then it is argued that claims of one kind are to be taken literally, whereas those of the other kind function in some different way.
This is not what I have in mind. I think of a physics theory as providing an explanatory scheme into which phenomena of interest can be fitted. I agree with Duhem here. The scheme simplifies and organizes the phenomena so that we can treat similarly happenings that are phenomenologically different, and differently ones that are phenomenologically the same. It is part of the nature of this organizing activity that it cannot be done very well if we stick too closely to
end p.77
stating what is true. Some claims of the theory must be literally descriptive (I think the claims about the mass and charge of the electron are a good example) if the theory is to be brought to bear on the phenomena; but I suspect that there is no general independent way of characterizing which these will be. What is important to realize is that if the theory is to have considerable explanatory power, most of its fundamental claims will not state truths, and that this will in general include the bulk of our most highly prized laws and equations.
2. Examples: Quantum Damping
In radiative damping, atoms de-excite, giving off photons whose frequencies depend on the energy levels of the atom. We know by experiment that the emission line observed in a spectroscope for a radiating atom is not infinitely sharp, but rather has a finite linewidth; that is, there is a spread of frequencies in the light emitted. What causes this natural linewidth? Here is the standard answer which physicists give, quoted from a good textbook on quantum radiation theory by William Louisell:
There are many interactions which may broaden an atomic line, but the most fundamental one is the reaction of the radiation field on the atom. That is, when an atom decays spontaneously from an excited state radiatively, it emits a quantum of energy into the radiation field. This radiation may be reabsorbed by the atom. The reaction of the field on the atom gives the atom a linewidth and causes the original level to be shifted as we show. This is the source of the natural linewidth and the Lamb shift.3
Following his mathematical treatment of the radiative decay, Louisell continues:
We see that the atom is continually emitting and reabsorbing quanta of radiation. The energy level shift does not require energy to be conserved while the damping requires energy conservation. Thus damping
end p.78
is brought about by the emission and absorption of real photons while the photons emitted and absorbed which contribute to the energy shift are called virtual photons.4
This account is universally agreed upon. Damping, and its associated line broadening, are brought about by the emission and absorption of real photons.
Here we have a causal story; but not a mathematical treatment. We have not yet set line broadening into the general mathematical framework of quantum mechanics. There are many ways to do this. One of the Springer Tracts by G. S. Agarwal5 summarizes the basic treatments which are offered. He lists six different approaches in his table of contents: (1) WeisskopfWigner method; (2) HeitlerMa method; (3) GoldbergerWatson method; (4) Quantum Statistical method: master equations; (5) Langevin equations corresponding to the master equation and a c-number representation; and (6) neoclassical theory of spontaneous emission.
Before going on to discuss these six approaches, I will give one other example. The theory of damping forms the core of current quantum treatments of lasers. Figure 4.1 is a diagram from a summary article by H. Haken on the quantum theory of the laser.6 We see that the situation I described for damping theory is even worse here. There are so many different treatments that Haken provides a family tree to set straight their connections. Looking at the situation Haken himself describes it as a case of theory overkill. Laser theory is an extreme case, but I think there is no doubt that this kind of redundancy of treatment, which Haken and Agarwal picture, is common throughout physics.
Agarwal describes six treatments of line broadening. All six provide precise and accurate calculations for the shape
end p.79
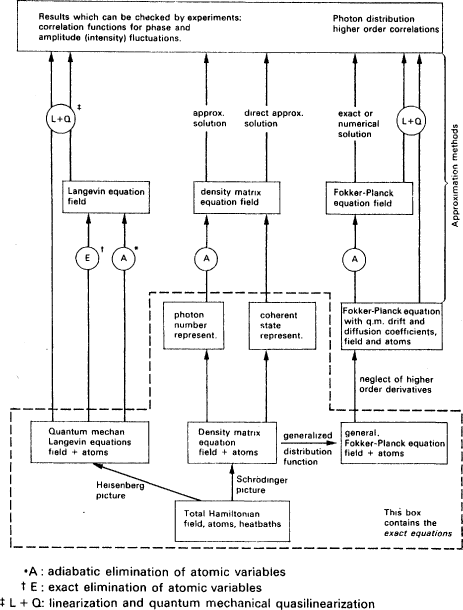
Fig. 4.1. Family tree of the quantum theory of the laser. (Source: Haken, The Semiclassical and Quantum Theory of the Laser.)
and width of the broadened line. How do they differ? All of the approaches employ the basic format of quantum mechanics. Each writes down a Schroedinger equation; but it is a different equation in each different treatment. (Actually among the six treatments there are really just three different equations.) The view that I am attacking takes theoretical explanations to provide, as best they can, statements of objective laws. On this view the six approaches that Agarwal lists compete with one another; they offer different laws for exactly the same phenomena.
But this is not Agarwal's attitude. Different approaches are useful for different purposes; they complement rather than compete. The Langevin and Master equations of (4) and (5), for instance, have forms borrowed from statistical mechanics. They were introduced in part because the development of lasers created an interest in photon correlation experiments. Clearly, if we have statistical questions, it is a good idea to start with the kind of equations from which we know how to get statistical answers.
Let us consider an objection to the point of view I have been urging. We all know that physicists write down the kinds of equations they know how to solve; if they cannot use one approximation, they try another; and when they find a technique that works, they apply it in any place they can. These are commonplace observations that remind us of the pragmatic attitude of physicists. Perhaps, contrary to my argument, the multiplication of theoretical treatments says more about this pragmatic orientation than it does about how explanatory laws ought to be viewed. I disagree. I think that it does speak about laws, and in particular shows how laws differ from causes. We do not have the same pragmatic tolerance of causal alternatives. We do not use first one causal story in explanation, then another, depending on the ease of calculation, or whatever.
The case of the radiometer illustrates. The radiometer was introduced by William Crookes in 1873, but it is still not clear what makes it work. Recall from the Introduction to these essays that there are three plausible theories. The first attributes the motion of the vanes to light pressure. This explanation is now universally rejected. As M. Goldman remarks in The Radiometer Revisited,
A simple calculation shows that on a typical British summer day, when the sky is a uniform grey (equally luminous all over) the torque from the black and silver faces exactly balance, so that for a perfect
end p.81
radiometer [i.e., a radiometer with a perfect vacuum] no motion would be possible.7
Two explanations still contend. The first is the more standard, textbook account, which is supported by Goldman's calculations. It supposes that the motion is caused by the perpendicular pressure of the gas in the perfect vacuum against the vanes. But as we have seen, on Maxwell's account the motion must be due to the tangential stress created by the gas slipping around the edge of the vanes. There is a sense in which Maxwell and Goldman may both be right: the motion may be caused by a combination of tangential and perpendicular stress. But this is not what they claim. Each claims that the factor he cites is the single significant factor in bringing about the motion, and only one or the other of these claims can be accepted. This situation clearly contrasts with Agarwal's different theoretical treatments. In so far as we are interested in giving a causal explanation of the motion, we must settle on one account or the other. We cannot use first one account, then the other, according to our convenience.
I know of this example through Francis Everitt, who thinks of building an experiment that would resolve the question. I mention Everitt's experiment again because it argues for the difference in objectivity which I urge between theoretical laws and causal claims. It reminds us that unlike theoretical accounts, which can be justified only by an inference to the best explanation, causal accounts have an independent test of their truth: we can perform controlled experiments to find out if our causal stories are right or wrong. Experiments of these kinds in fact play an important role in an example from which Wesley Salmon defends inferences to the best explanation.
3. The Argument from Coincidence
In a recent paper8 Salmon considers Jean Perrin's arguments for the existence of atoms and for the truth of Avagadro's
end p.82
hypothesis that there are a fixed number of molecules in any gram mole of a fluid. Perrin performed meticulous experiments on Brownian motion in colloids from which he was able to calculate Avagadro's number quite precisely. His 1913 tract, in which he summarizes his experiments and recounts the evidence for the existence of atoms, helped sway the community of physicists in favour of these hypotheses. Besides Brownian motion, Perrin lists thirteen quite different physical situations which yield a determination of Avogadro's number. So much evidence of such a variety of kinds all pointing to the same value must surely convince us, urges Perrin, that atoms exist and that Avogadro's hypothesis is true.
For many, Perrin's reasoning is a paradigm of inference to the best explanation; and it shows the soundness of that method. I think this misdiagnoses the structure of the argument. Perrin does not make an inference to the best explanation, where explanation includes anything from theoretical laws to a detailed description of how the explanandum was brought about. He makes rather a more restricted inferencean inference to the most probable cause.
A well-designed experiment is constructed to allow us to infer the character of the cause from the character of its more readily observable effects. Prior to Perrin, chemists focused their attention on the size and velocities of the suspended particles. But this study was unrewarding; the measurements were difficult and the results did not signify much. Perrin instead studied the height distribution of the Brownian granules at equilibrium. From his results, with a relatively simple model for the collision interactions, he was able to calculate Avogadro's number. Perrin was a brilliant experimenter. It was part of his genius that he was able to find quite specific effects which were peculiarly sensitive to the exact character of the causes he wanted to study. Given his model, the fact that the carrier fluids had just 61023 atoms for every mole made precise and calculable differences to the distribution he observed.
The role of the model is important. It brings out exactly what part coincidence plays in the structure of Perrin's argument. Our reasoning from the character of the effect
end p.83
to the character of the cause is always against a background of other knowledge. We aim to find out about a cause with a particular structure. What effects appear as a result of that structure will be highly sensitive to the exact nature of the causal processes which connect the two. If we are mistaken about the processes that link cause and effect in our experiment, what we observe may not result in the way we think from the cause under study. Our results may be a mere artefact of the experiment, and our conclusions will be worthless.
Perrin explicitly has this worry about the first of the thirteen phenomena he cites: the viscosity of gases, which yields a value for Avogadro's number via Van der Waal's equation and the kinetic theory of gases. In his Atoms he writes that the probable error, for all these numbers is roughly 30 per cent, owing to the approximations made in the calculations that lead to the Clausius-Maxwell and Van der Waal's equations. He continues: The Kinetic Theory justly excites our admiration. [But] it fails to carry complete conviction, because of the many hypotheses it involves. (I take it he means unsubstantiated hypotheses.) What sets Perrin's worries to rest? He tell us himself in the next sentence: If by entirely independent routes we are led to the same values for the molecular magnitudes, we shall certainly find our faith in the theory considerably strengthened.9
Here is where coincidence enters. We have thirteen phenomena from which we can calculate Avogadro's number. Any one of these phenomenaif we were sure enough about the details of how the atomic behaviour gives rise to itwould be good enough to convince us that Avogadro is right. Frequently we are not sure enough; we want further assurance that we are observing genuine results and not experimental artefacts. This is the case with Perrin. He lacks confidence in some of the models on which his calculations are based. But he can appeal to coincidence. Would it not be a coincidence if each of the observations was an artefact, and yet all agreed so closely about Avogadro's number?
end p.84
The convergence of results provides reason for thinking that the various models used in Perrin's diverse calculations were each good enough. It thus reassures us that those models can legitimately be used to infer the nature of the cause from the character of the effects.
In each of Perrin's thirteen cases we infer a concrete cause from a concrete effect. We are entitled to do so because we assume that causes make effects occur in just the way that they do, via specific, concrete causal processes. The structure of the cause physically determines the structure of the effect. Coincidence enters Perrin's argument, but not in a way that supports inference to the best explanation in general. There is no connection analogous to causal propagation between theoretical laws and the phenomenological generalizations which they bring together and explain. Explanatory laws summarize phenomenological laws; they do not make them true. Coincidence will not help with laws. We have no ground for inferring from any phenomenological law that an explanatory law must be just so; multiplying cases cannot help.
I mentioned that Gilbert Harman introduced the expression inference to the best explanation. Harman uses two examples in his original paper.10 The first is the example that we have just been discussing: coming to believe in atoms. The second is a common and important kind of example from everyday life: inferring that the butler did it. Notice that these are both cases in which we infer facts about concrete causes: they are not inferences to the laws of some general explanatory scheme. Like Perrin's argument, these do not vindicate a general method for inferring the truth of explanatory laws. What they illustrate is a far more restrictive kind of inference: inference to the best cause.
4. Conclusion
Perrin did not make an inference to the best explanation, only an inference to the most probable cause. This is typical of modern physics. Competing theoretical treatmentstreatments that write down different laws for the same phenomenaare encouraged in physics, but only a single causal story is allowed. Although philosophers generally believe in laws and deny causes, explanatory practice in physics is just the reverse.
end p.86
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2273
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved