| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
MECHANICS OF MATERIALS
CYCLE OF LECTURES
COMPOUND STRESSES
CONTENT
2. Position of a neutral axis . . 6
3. Strength requirements for a straight rod . . . . . . . . . . . . . . . . 9
4. Kern of a cross section . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5. Strength requirements for initially curved beams . . . . . . . . .15
6. Thin-walled pressure vessels . . . . . . . . . . . . . . . . . . . . . . . . 19
1. Stresses at any point
Structural members discussed up to this chapter were loaded very simply. Therefore single internal forces there in cross sections were met: only an axial force (pure tension or compression), only a shearing force (shearing), only a torque (torsion), only a bending moment (pure bending). The only case where we have dealt with two internal forces was bending: a bending moment and shearing force.
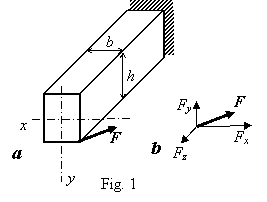
Most of the structural members are loaded not so
simply, and distribution of internal forces very often is more complicated. The
most complicated case is that one when in a cross section there all the six
internal forces are acting. Even some simple loading can cause complicated
distribution of stresses. For example, the only force applied in a direction
which does not cross any principal axis or the longitudinal axis of the member
and is not parallel to these axes (Fig. 1, a)
causes a complicated deformation: the presentation of the force by its
components (Fig. 1, b) makes the
values of internal forces clear:
(z is
the distance of the cross section from the free end of the cantilever).
 If the direction of the force F applied to the cantilever shown in Fig. 1 is not crossing axis z, is
perpendicular to this axis and not coinciding with any principal axis (as
shown in Fig. 2), axial force N = Fz = 0 and torque T = 0, only two
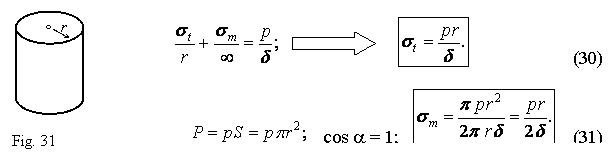
bending moments and two shearing forces are acting in all the sections of the
cantilever. Such a very often loading is called skew bending or
oblique bending (sometimes unsymmetrical
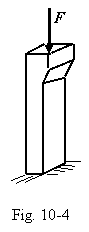
bending). The angle under its own weight loading g (Fig. 3) is causing skew bending also because the load direction
does coincide with neither principal axis u
nor v.
If the direction of the force F applied to the cantilever shown in Fig. 1 is not crossing axis z, is
perpendicular to this axis and not coinciding with any principal axis (as
shown in Fig. 2), axial force N = Fz = 0 and torque T = 0, only two
bending moments and two shearing forces are acting in all the sections of the
cantilever. Such a very often loading is called skew bending or
oblique bending (sometimes unsymmetrical
bending). The angle under its own weight loading g (Fig. 3) is causing skew bending also because the load direction
does coincide with neither principal axis u
nor v.
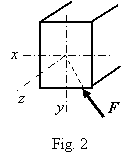
Another simple loading causing composed stresses is eccentric tension or eccentric compression: the only force causes an axial force and bending moments (Fig. 4).
We are able to determine the stress distribution when any internal force component is acting alone. When several components are acting the stress distribution is more complicated. It may be determined by the principle of superposition when this principle is valid (it is applicable when displacements are small and Hookes law is valid).
We know that normal stresses in cross sections are related only to the axial force N and the bending moments Mx, My:
 (1)
(1)
Shearing stresses are related only to three components also:
 (2)
(2)
Stresses are vectors and should be summed according to the rules of vectorial addition. All the components of the normal stresses are directed parallel to the longitudinal axis z (Fig. 5), therefore the value of the resulting normal stress at any point k is equal to an algebraic sum of all the values obtained by the formulae (1):
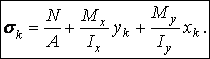 (3)
(3)
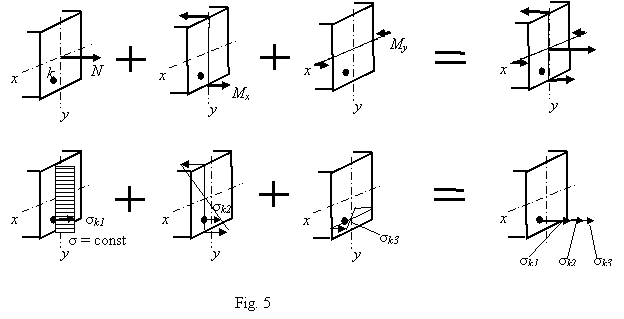 Do not forget that x
and y here as well as in the formulae
(1) are related to the principal centroidal axes of the cross section.
Do not forget that x
and y here as well as in the formulae
(1) are related to the principal centroidal axes of the cross section.
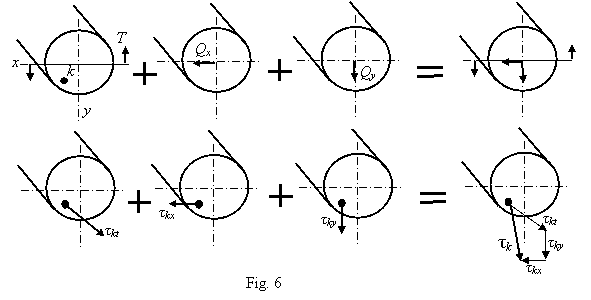
Shearing stresses related to different internal force components are acting in different directions (Fig. 6). Their values can be calculated by (2) but no algebraic summation is applicable, the resulting stress should be found as a vector sum:
![]() (4)
(4)
An algorithm for solving any problem related to compound stresses:
1. Divide all the given loading in two parts one acting in one principal plane and other acting in another principal plane.
2. Plot the diagrams of shearing force and bending moments for both principal planes. Separately plot the diagrams of torques and axial forces. Determine the dangerous sections by analysing all the diagrams together.
3. Determine the normal and shearing stress distributions in every dangerous section separately from every internal force component. Determine the dangerous points in cross sections by analysing all the distributions together.
4. Determine stress state in every dangerous point and write the strength requirement which is simple for one-dimensional state and more complicated (based on hypotheses) for other cases.
5. If stiffness requirements should be satisfied, calculate displacements separately in both principal planes and after that determine a vector sum of all the components of any displacement.
 2. Position of a neutral
axis
2. Position of a neutral
axis
Fibres in the so-called neutral surface (NS)
of a straight rod are not stressed at all. Intersection of this surface
with a cross section (Fig. 7) is termed neutral
axis (NA). Normal stresses in this line are equal zero. Therefore an
equation of the neutral axis can be obtained from the expression of normal stress
at any point (taken off the co-ordinate indices):
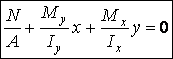
It is obvious that the largest values of normal
stresses are at the points which are the most remote from the neutral axis
(compare Fig. 7). Position of the neutral axis is used for determining positions
of these dangerous points: you should draw tangent lines parallel to the
neutral axis (Fig. 8), and the points of touching the cross-sectional
boundary are those of extreme stresses.

![]()
![]() Neutral
axis divides the cross section into two areas: with positive normal stresses
(the tensile part) and with negative (the compressive one).
Neutral
axis divides the cross section into two areas: with positive normal stresses
(the tensile part) and with negative (the compressive one).
Two cases of the neutral axis position could be analysed: when N = 0 and when N ¹ 0. The first case is termed skew bending or oblique bending. The absolute term in the neutral axis equation is equal zero in this case; it means that the neutral axis is passing the origin of the co-ordinate system, i. e. the centroid of the cross section. The equation can be written as follows:
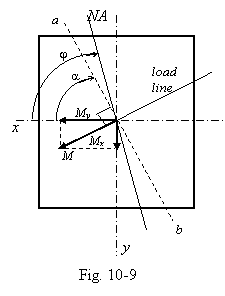
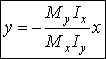 (6)
(6)
The both bending moments (Mx and My)
can be replaced by the resultant vector sum M (Fig. 9). This moment is acting in a plane which is termed as
load plane (its intersection with
the cross-sectional plane is load
line).
here
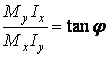 (Fig. 9).
(Fig. 9).
The neutral axis usually is not perpendicular to the load line as it was proved in the case of simple bending: now ½j½ ³ ½a½. The neutral axis is nearer to the co-ordinate axis of the minimum moment of inertia.
|
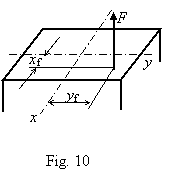
Even in the case of any complicated loading we can apply the only force loading image for the analysis of normal stresses: having values N, Mx and My, we can determine the value of the resultant load force F and the co-ordinates of its application point xf = My/N, yf = Mx/N. Applying these expressions the equation of the neutral axis is presented as follows:
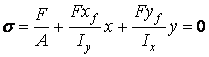 (7)
(7)
or (applying expression of
squared radius of gyration Ix/A
= i![]() )
)
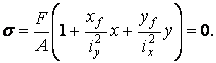 (8)
(8)
The expression between brackets is equal to zero because F/A ¹
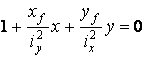 (9)
(9)
or
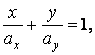 (10)
(10)
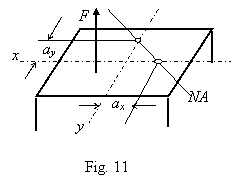
where
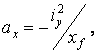
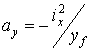 (11)
(11)
are
co-ordinates of two points at which the neutral axis is crossing co-ordinate
axes (as shown in Fig. 11). The sign of ax
is contraverse to the sign of xf
because ![]() is positive. Therefore
is positive. Therefore
|
the neutral axis is crossing the quadrant which is crosswise opposite to the quadrant of the resultant load force application. |
10.3. Strength requirements for a straight rod
When no torque and no shearing force are acting in a cross section, no shearing stress there is. The state of stresses is one-dimensional. Shearing stresses caused by shearing forces are small and negligible. The only torque causes shearing stresses large significantly, especially at boundary points. Such shearing stresses should be considered, and in this case the state of stresses is multidimensional. So, the strength requirements are different for the next two cases:
|
one-dimensional state of stresses |
multidimensional state of stresses |
|
|
t or t (T = 0) |
t ¹ (T ¹ |
One-dimensional state (T = 0)
The points with extreme values of
normal stresses are decisive when strength of a rod is under consideration.
Those are the points most remoted from the neutral axis. Tangent lines
parallel to the neutral axis help to fix these boundary points (Fig. 12).

Strength requirements for the shown section are two restrictions for smax at the point k and for smin at the point j:
![]()
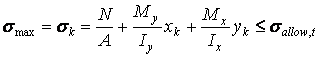
![]()
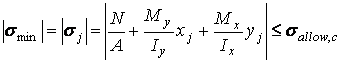 (13)
(13)
When you have determined the co-ordinates of the extreme points k and j, applying strength requirements (12) and (13) is simple.
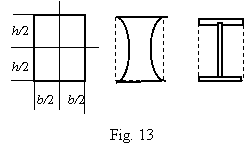
Simplier strength requirements are for cross sections which shape is
rectangle or another figure with four symmetrical corners (Fig. 13). The
co-ordinates of these corners are equal but with different signs: h/2
and b xmax and ymax).![]()
Applying Ix/ymax = Wx and Iy/xmax = Wy, we have the following expressions of the
strength requirements, valid only for rectangular or similar
symmetrical shapes of cross sections:
only for
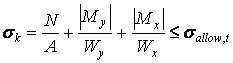 (14)
(14)
![]()
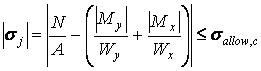 (15)
(15)
These expressions of the strength requirements are for the four corners of the rectangular cross section (inspite of the absense of the co-ordinates of these corners).
Two-dimensional state (T ¹
When both normal and shearing stresses are acting at any point of a cross section, state of stresses is two-dimensional. Usually shearing stresses caused by shearing forces are negligible, and only torques make to include shearing stresses into strength requirement formulations.
Hypotheses of failure and plasticity are applied when formulating strength requirements for the two-dimensional state of stresses. Having normal stress sk and shearing stress tk at some decisive (the most dangerous) point of a cross section, strength requirement can be expressed according to the energy hypothesis as
![]() (16)
(16)
or according to the maximum shearing stress hypothesis as
![]() (17)
(17)
Do not forget: both normal and shearing stress values in the expressions (16) and (17) should be determined for the same point k. This the most dangerous point can be found after calculating and comparing normal stresses caused by axial force N and bending moments Mx, My, shearing stresses caused by torque T and shearing forces Qx, Qy.
The requirement is simple when axial force is absent in the cross
section (N = 0). The bending
moments may be summed (Fig. 14): The points a and b are in the plane where bending
moment M is acting; there extreme
normal stress values smax smin should be.
Strength requirements can be expressed simplier
when the cross section is circular, because in this case all
the geometric parameters may be expressed by one dimension diameter d.
![]()
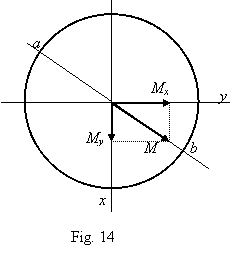
The shearing stresses caused by the torque T have their extreme values at the boundary points too, therefore the points a and b are the most dangerous. When axial force N = 0, values of the extreme normal stresses at these points are equal: sa sb ; it means that the value of normal stress at any of these points is
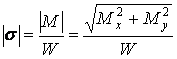 (18)
(18)
Shearing stress at any of these points (having an expression of polar section modulus Wp = Wx + Wy = 2W):
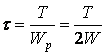 (19)
(19)
Then
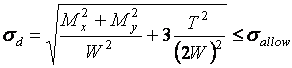 (20)
(20)
and
or
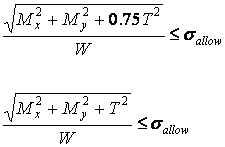
only for circular sections!
(energy hypothesis)
![]() or
or
tmax hypothesis)
There W is axial section modulus (W = pd
These
formulae are very handy for design, therefore they often are applied even in
the cases when N, Qx and Qy should be considered: the required section modulus W is determined at first without any
consideration of these N and Q, after that stresses s and t are calculated with the consideration and
the strength requirement ![]() checked.
checked.
section
(Fig. 15) eventual positions of smax
and smin
are at corners a, b, c, d, but shearing
stresses t
at these points are equal zero. At points e, f, m, n values of shearing stresses are large, but values of normal
stresses are less. Only after calculation
The circular (and tubular) cross section is
peculiar because the point of the maximum normal stress coincides with the
point ot the maximum shearing stress. In
other cross-sectional shapes these
points do not coincide: in any rectangular cross
![]() or
or ![]() for all the shady points k you can decide which of them is the most dangerous.
for all the shady points k you can decide which of them is the most dangerous.

10.4. Kern of a cross section
Masonry and some other structural materials resist compression very well but do not resist tension. An engineer should exclude any tensile stresses in masonry; all the normal stresses should be negative there. This statement means that the neutral axis should not cross the area of a cross section.
When the neutral axis is at
significant distance from the centroid of the cross-sectional area, the
co-ordinates of the intersection ax,
ay are large, and
therefore the co-ordinates of the loading point are small (![]() ).
So, the designer should apply the load close to the centroid if he seeks not to
meet tension. The load should be applied within the small area surrounding the
centroid.
).
So, the designer should apply the load close to the centroid if he seeks not to
meet tension. The load should be applied within the small area surrounding the
centroid.
This zone of the cross-sectional area applying within which a compressive load does not cause tensile stress anywhere in the section is called the kern (or core) of a section.
Boundary points of the kern can be determined by the following formulae:

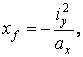
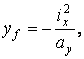 (23)
(23)
where ax, ay
are co-ordinates of the points of intersection between co-ordinate axes
and tangents of the cross-sectional contour as shown in Fig. 16 for the
tangent 1-1 and the coinciding kern boundary
corner point 1 with co-ordinates xf1, yf1.
As an example a kern of a rectangular cross section is determined (Fig. 17). There is shown calculation of co-ordinates of one corner point of the kern boundary; other corners are determined analogously.
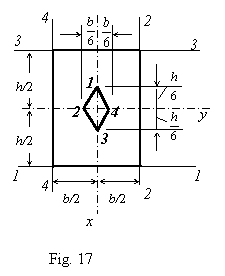
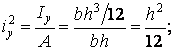
![]()
![]() Þ
Þ 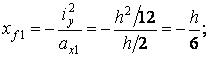
![]() ; Þ
; Þ ![]() .
.
 As the example has shown, the kern of any rectangular
cross section has a shape of diamond. It is easy to prove that the kern of a
circular cross section with diameter D is
also circular with diameter d = D/4.
As the example has shown, the kern of any rectangular
cross section has a shape of diamond. It is easy to prove that the kern of a
circular cross section with diameter D is
also circular with diameter d = D/4.
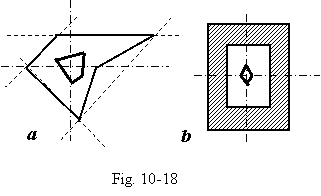
Any kern
is convex, even when the boundary of cross-sectional area is not convex
(Fig. 18, a). In some cases (Fig.
18, b) kern can be in a hole
area.
Do not forget the main purpose of the kern: it determines the part of the cross-sectional area in which you may apply a load without causing different (positive and negative) normal stresses in the whole cross section.
10.5. Strength requirements for initially curved beams
There are many structures consisting of initially curved beams: arches (Fig. 19, a), rims of wheels (b), hooks (c) etc There in this item only plane curved beams will be investigated; the axis of a plane beam and all its loads are lying in a plane of symmetry (the investigation will not cover structures similar to that one shown there in Fig. 19, d). We will discuss the beams which cross sections have dimensions comparable with the radius of curvature (a r, see Fig. 20) it means that this radius is very small and the curvature is large.
Deformation
of initially curved beams is complicated by the next two peculiarities: 1)
distribution of internal forces N,
M, Q along the axis is not linear; 2) distribution of stress and
strain in a cross section is not linear too (in spite of the validity of
the Bernoullis hypothesis). Polar
co-ordinate an angle j is usually applied for defining the
location of any cross section in a curved beam. The sign rule for bending moments is
following: bending moment is positive when it increases the initial
curvature.

Method of sections is applied for estimating internal forces. It is illustrated by an example (Fig. 21).

The internal forces are calculated applying equilibrium equations (SFz= S Fy= S Mc=
![]()
![]()
![]()
Let be F1 = 5F and F2 = 4F, then internal forces ![]()
![]()
![]() and their diagrams are presented in Fig. 22.
and their diagrams are presented in Fig. 22.
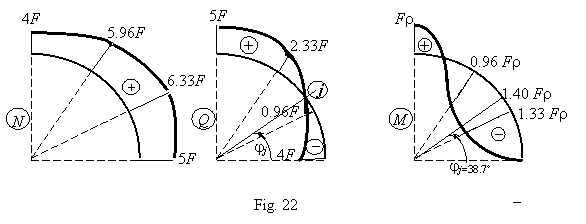
Calculation of the co-ordinate jj for the position of the Mextreme:
![]()
![]()
![]()
Mextreme = Mj = Fr(5 5cos38.7 4 sin38.7 1.40Fr
So we have a simple curved structure and very complicated, nonlinear distributions of internal forces.
Now let us consider normal stresses in a cross section. They may be caused by an axial force and by a bending moment. Normal stresses caused by N are constant in all the area of the cross section (the distribution is the same as in a cross section of a straight rod). The distribution of normal stresses caused by the bending moment is not linear but hyperbolic (Fig. 23).

An expression for the normal stress at any point k:
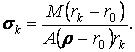 (24)
(24)
There in the formula (24) A is an area of the cross section, rk a distance between the point k and the centre of curvature, r0 a distance between the neutral axis and the centre of curvature. The latter distance is expressed as follows:
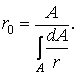 (25)
(25)
There in literature expressions of r0 for various shapes of cross section (rectangular, triangular, circular a. o.) are presented.
If you want to sattisfy strength in an initially curved beam, you should:
to find the extremum bending moment Mj;
to find the value of the axial force Nj at the section with extremum bending moment;
to estimate the position of the neutral axis in this section (when only bending moment is acting);
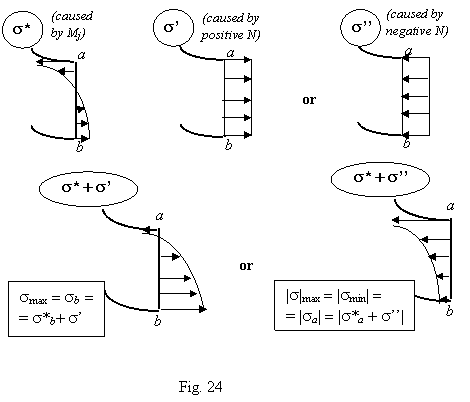
to calculate normal stresses caused by Nj and Mj, to sum them at the most dangerous point (Fig. 24), to check if the strength requirements are sattisfied:
![]()
![]()
10.6. Thin-walled pressure vessels
The vessel is called thin-walled when the ratio between
the diameter d of the vessel and
the thickness d
of its walls is very large (d/d >
20). These vessels have a shape of a sphere, of a cylinder, of a paraboloid
etc. They are used as reservoirs, boilers, tubes, and are acted by an
internal pressure of fluids or gas. We
will
All the considerations in the course were related mostly to
rods, bars, beams. In this item you will get an aquaintance with some kind of
shells, with axisymmetrical shells of revolution (Fig. 25), with so-called
thin-walled pressure vessels. Such vessels are very popular, and estimating
stress and strain in them is not complicated.
consider only the vessels with symmetrical loading (Fig. 26, a) because in this case a vessel acts as a membrane, i. e. bending of the walls does not take place. When the

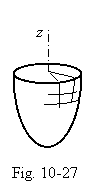
A symmetrical thin-walled vessel acted by an internal symmetrical pressure p is under consideration.A segment of the vessel wall (Fig. 27) is isolated from this vessel by passing two planes trough the axis of symmetry z and two circular sections which are perpendicular to the exernal surface. This segment is presented in Fig. 28. There in two meridional cuts (ad and bc) circumferial (or hoop) stresses st are acting; meridional (or longitudinal) stresses sm are acting in two hoop cuts (ab and dc). No shearing stress is in these cuts, therefore the stresses st and sm are principle stresses. Stresses in the third direction, in the radial one, are very small, negligible. It means that the stress state is twodimensional.
The separated element of the shell is acted by
five resultant forces: 1) a resultant of the loading which is equal to
the product of the internal pressure and the area of the internal surface: p dst dsm;
this resultant is perpendicular to the inernal surface of the shell, it is
not shown in Fig. 28;
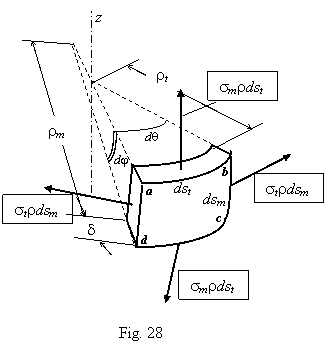
2) four resultants of normal stresses two smrdst and two strdsm; the lines of these resultants does not coincide, between directions of both equal forces there are small angles (dj and dq
The equilibrium equation (the sum of projections of all the five forces to the axis perpendicular to the surface of the shell is equal zero):
![]()
Angles are very small, therefore
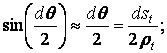
![]()
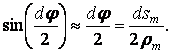
After substituting these expressions into equation we have:
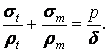 (26)
(26)
 There
in the equation two unknown quantities are included: st and sm. Therefore we need one more
equation.
There
in the equation two unknown quantities are included: st and sm. Therefore we need one more
equation.
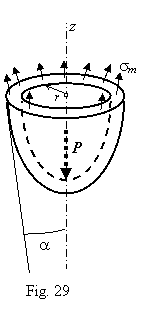
Such an equation can be obtained by equilibrium of the
cut part of the vessel as shown in Fig. 29: There a - an angle between the axis z and the direction of sm, P a
resultant of all the internal pressure acting on the separated part of the
vessel. Thus
![]()
![]()
![]() (27)
(27)
When the pressure p is constant (for example, pressure of gas),
P = pS,
where
S is an area of a projection of
the internal surface of the separated part to the plane perpendicular to
the axis of symmetry z. When the
pressure is caused by a liquid in a vessel, then (Fig. 30):
![]() (29)
(29)
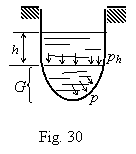
there G is the weight of the liquid contained in the separated part of vessel.
We see that ![]() in a cylindrical vessel. Hoop stresses there
are twice more dangerous than meridional ones (you can prove it when inflating
a cylindrical rubber balloon up to its burst: crack will be meridional caused
by hoop stresses).
in a cylindrical vessel. Hoop stresses there
are twice more dangerous than meridional ones (you can prove it when inflating
a cylindrical rubber balloon up to its burst: crack will be meridional caused
by hoop stresses).
In a spherical
vessel p = const, ![]() and the equation (26) can be solved without
supplementary equations; there
and the equation (26) can be solved without
supplementary equations; there ![]() and
and
![]()
![]() ,
, 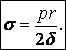 (32)
(32)
The strength requirements for thin-walled pressure
vessels are composed by applying any strength hypothesis because the stress
state is two-dimensional. For example, when the energy hypothesis is applied (![]() ,
,
![]() )
)
![]() (33)
(33)
Any
designer knows that both st
and sm are
positive and ![]() Therefore a stronger hypothesis often is
applied the hypothesis of maximum normal stress:
Therefore a stronger hypothesis often is
applied the hypothesis of maximum normal stress:
![]() (34)
(34)
All these formulae are valid for the estimation of stress and strength at points remote from any break in a surface of the vessel (for example, from head of a boiler). At any breaking the strain state is more complicated, the head of the boiler is preventing a uniform deformation, the shell is bended, there can be noticed a so-called fringe effect (or edge effect). Consideration of any fringe effect is complicated but very important. This effect was one of the reasons of the failure of a vessel in Jonava plant Azotas.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3720
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved