CAPACITY PLANNING

1 Introduction

This chapter aims to introduce and discuss the capacity expansion planning process in firms as a prelude to further discussion of the related location factors.

2 Definition of Capacity

The capacity of an operation has been defined in several ways in the literature with the main themes used being the level of output and the time available for the operation. Slack et al (2001: 338) define capacity as the maximum level of value-added activity over a period of time that the process can achieve under normal operating conditions while Martinich (1997: 252) defines it as the rate at which the output can be produced by an operating unit [] expressed in terms of the number of units of output produced per unit of time. Therefore, the capacity of an operation sets an upper limit on the amount of output that can be made available to service customer demand.

3 Measurement of Capacity

Blackstone (1989: 8) states that the unit of measure chosen for capacity should be common among the mix of products be they pieces, tons or standard hours. Hill (2000: 170) notes that though time and money are the common denominators used in business to measure activities, in operations the common denominator tends to be the time taken to complete the particular operation. Using money would be inappropriate since as Stevenson (2002: 175) states it is important to choose a measure of capacity that does not require updating. In this case, price changes would necessitate updating of the capacity measure. Capacity can therefore be measured in a number of ways depending on how the output is measured and the operating conditions assumed (Martinich, 1997: 252).

3.1 Capacity as a measure of output

From the definition of capacity above, it would seem that measuring capacity would be straightforward as it would simply be the maximum number of units produced in a given time. However, this is only feasible when the operation has one product as an output (Stevenson, 2002: 175 and Martinich, 1997: 252). Output measures are best utilised when the firm produces a relatively small number of standardised or similar products (Krajewski and Ritzman, 2001: 325 and Martinich, 1997: 252). Therefore, in the case of a tyre plant, its capacity would be defined as the maximum number of tyres that can be produced in a specified time period of for instance an hour, a day, a week, a month or a year.

Operations differ in their level of complexity with many organisations having more than one product on offer (Krajewski and Ritzman 2001: 325). This makes the measurement of capacity difficult since these products may have different output rates (Martinich, 1997: 252). For instance, a shoe firm could be said to have a capacity to make either 500 sandals or 250 shoes per day. However, if the operation has several other products, then describing capacity with respect to all the products may prove cumbersome (Stevenson 2002: 175).

In addition, due to the varying demand of the sandals and shoes it may be necessary to produce a combination of the two items. Therefore, it would no longer be appropriate to talk of the capacity output in total units without mentioning the products (Stevenson, 2002: 175 and Martinich, 1997: 252). A possible combination of the two items could give a capacity of say 300 sandals and 100 shoes per day or 200 sandals and 150 shoes per day. The choice of the product mix will therefore have an effect on the operations capacity.

Given the need to have a measure of capacity that does not require updating (Stevenson 2002: 175) it then follows that with increasing variety in the product mix, the use of output-based capacity measures becomes less useful (Krajewski and Ritzman, 2001: 325 and Slack et al, 2001: 344). In such cases of a varied and wide product mix of outputs, the availability of inputs to the operation is used as a measure of capacity (Martinich, 1997: 252; Slack et al, 2001: 344 and Stevenson, 2002: 175). The inputs to the operation can be in the form of machine hours available for a factory, number of beds available in a hospital, number of seats available in an airplane or a bus, and so on.

Slack and Lewis (2002: 114) state that input measures are used usually because there is no clear relationship between the input and the output. The output may fluctuate depending on the product mix but normally the input remains constant thus making it an appropriate measure of capacity. For instance the number of seats in a theatre may remain fixed although the number of customers watching plays may fluctuate depending on other factors such as the type of play shown, the day of the week, the weather and so on.

In summary, output measures are usually chosen for high-volume (low-variety) processes while input measures are used for low-volume (high variety) processes with high flexibility (Krajewski and Ritzman 2001: 325). Slack et al (2001: 344) state that whereas most operations may use a mix of the input and output measures of capacity, they tend to use only one of these two measures of capacity as indicated in table 1 below:

Table Input and output measures of capacity for different operations

Source: Slack et al (2001). Operations Management (3^rd Edn), Pearson Education, p344.

3.2 Capacity as defined by operating conditions

The conditions under which a system is assumed to operate also affect the measurement of capacity (Martinich, 1997: 252). As Stonebraker and Leong (1994: 146) state, capacity has been defined in three different ways in the literature with the distinctions being made in the way it is measured. 

Design capacity is the maximum output per time period achievable on a continual basis under ideal conditions (Stonebraker and Leong, 1994: 146; Martinich, 1997: 252 and Stevenson, 2002: 176). The design capacity is essentially the level of output that the equipment supplier specified when designing the machine and it is assumed that the equipment will be available at all times for production.

However, most firms operate their facilities at less than the design capacity because they have found that they can operate more efficiently when their resources are not stretched to the limit (Heizer and Render, 2001: 252). This is because achieving design capacity requires the use of all the time available thus, creating the need to use overtime and extra shifts while reducing the maintenance activities. This can not be sustained for long because workers do not want to work for excessive overtime over extended periods, then also the extra cost of having overtime and extra shifts drives up operating costs while quality may deteriorate with a stretched workforce (Krajewski and Ritzman, 2001: 327).

Effective capacity is therefore the output per time period that can be realistically achieved under normal conditions given various operating constraints, such as product mix, maintenance, machine set ups, quality and other known or anticipated scheduling realities (Stonebraker and Leong, 1994: 146). Some of the anticipated scheduling realities include accommodating weekends, holidays and meal breaks during working time. Krajewski and Ritzman (2001: 327) stress that this output must be one that a firm can economically sustain under normal conditions.

After taking into consideration the anticipated scheduling problems, it is found that the actual output is usually less than the effective capacity over the long term due to demand fluctuations, which necessitate output changes, unexpected production disruptions and an intentional desire to reserve excess capacity for emergencies (Martinich, 1997: 252). The production disruptions may be due to quality problems, worker absenteeism, machine breakdowns, material shortages and other factors outside the control of the firms managers (Stevenson, 2002: 176 and Slack et al, 2001: 345).

3.3 Capacity performance measures

There are two ratios (capacity utilisation and capacity efficiency) available to aid in the assessment of how a firms production capacity is being used (Martinich, 1997: 253).

Capacity utilisation is a ratio of the actual output to the design capacity and is thus a measure of how much of the machinerys design capacity is actually utilised.

Capacity utilisation = Actual output

Design capacity

Capacity efficiency is the ratio of the actual output to the effective capacity and is thus a measure of how the system is able to operate within its operating constraints. It is a measure of how well the unanticipated scheduling difficulties were managed, thus a reflection of the managements capability.

Capacity efficiency = Actual output

Effective capacity

Stevenson (2002: 176) argues that whereas managers tend to be overly concerned with the efficiency of their operations, this emphasis may be misleading especially when the effective capacity is much less than the design capacity. This is because in such a case, high efficiency would imply an efficient use of effective capacity whereas the utilisation of the design capacity would be low.

Since the effective capacity acts as an upper limit on the actual output from the operation, Martinich (1997: 253) and Stevenson (2002: 177) state that it would be better if managers focused on improving the capacity utilisation by reducing the difference between effective and design capacity. This can be done by tackling problems in quality, maintenance, technical capabilities of workers and production scheduling usually at little or no cost in order to fully utilise the equipment (Martinich, 1997: 253).

Stevenson (2002: 177) sounds a warning that the benefits of high capacity utilisation can only be realised when there is demand for the product. Thus he notes that when demand is insufficient, high utilisation can be counterproductive since producing the excess output requires additional variable costs as well as costs of having to carry the output as inventory. Bradley and Arntzen (1999) note that even in the event when there is demand for a product, maximising capacity utilisation is not always the best financial strategy as it can lead to an inappropriate balance of inventory and capacity. They suggest that a simultaneous consideration of capacity, production, and inventory decisions would make it possible to increase capacity and lower inventories resulting in superior financial results.

4 Factors affecting effective capacity

Having discussed the performance measures of capacity, it is now necessary to understand the reasons why effective capacity is less than the design capacity. There are a number of factors that are known to affect the effective capacity of a system and Martinich (1997: 253-254) names the following as the most important;

• Process design - In a multi-stage production process, the maximum achievable rate of output is regulated by either the stage that is slowest or with the lowest capacity.
• Product design Given an identical set of personnel and equipment, the capacity of a process making a product that is well designed for production will be greater than that for a poorly designed one.
• Product variety With the volume-variety paradigm in mind, the lesser the variety of products that can be made by a production unit, the more volume that can be expected to be produced. This is because less time is lost on product changeovers and machine set-ups.
• Product quality The quality assessment methods employed by a firm will affect the rate at which products of acceptable quality can be produced. In some instances, work methods, testing and inspections intended to improve quality may reduce production capacity; whereas in other cases, these methods with the resulting reduction of product defects can increase effective capacity.
• Production scheduling Production scheduling that aims to minimise unproductive time leads to better utilisation of machines and personnel resulting in greater effective capacity.
• Materials management Material shortages can disrupt work, while excess inventories can cause congestion resulting in wasted time searching for materials. The availability of adequate stocks enhances productivity and capacity.
• Maintenance Equipment needs to be maintained in order to avoid breakdowns as well as defects due to machine wear which are major sources of lost production.
• Job design and personnel management The personnel operating a system directly influence the actual output that may be achieved. Inadequate training, poor job design, overwork, motivation and absenteeism all lead to lost production.

5 Capacity planning

A manufacturing strategy is developed to support the corporate and business strategy of a manufacturing business (Hayes and Wheelwright, 1984: 30). Capacity is one of the strategic decision categories that a firm needs to make policy on when formulating its manufacturing strategy (Olhager et al 2001). It is considered to be a structural decision because of its long-term impact on a firm, the difficulty involved in reversing it once it is in place and the fact that a substantial capital investment is required to adjust it (Hayes and Wheelwright, 1984: 31).

In other words, the objective of strategic capacity planning is to provide an approach to determining how the overall capacity level of capital-intensive resources such as facilities, equipment and overall labour size should be managed in order to best support the firms long-term competitive strategy (Chase et al, 2001: 356 and Silva 1994).

5.1 Capacity planning levels

As Olhager et al (2001) note, the management of capacity in a manufacturing firm is often divided into three or four stages, ranging from long-term capacity planning to short-term capacity control and execution. The relevant issues treated at the long-term capacity management level are related to determining when and by how much the capacity levels should change leading to investment in new facilities and equipment.

Medium-term capacity decisions determine the workforce level and production output level for the medium term within the physical capacity set by the long-term capacity decisions. Short-term capacity decisions are in turn constrained by the medium-term capacity decisions; they allocate the available capacity by assigning it to specific tasks, activities, or jobs. It may be concluded that at each level of capacity planning, the activities are quite similar though there are some distinctions in terms of time periods, inputs and outputs as well as the detail of the resource management method (Stonebraker and Leong, 1994: 145) as illustrated in table 2 below.

Table Three levels of capacity decisions

Source: Slack, N. and Lewis, M. (2002) Operations strategy. Pearson Education, p.119

5.2 Importance of capacity planning

Capacity expansion decisions are among the most fundamental of all the manufacturing strategy design decisions that managers, both in terms of the amount of capital required and the complexity of the decision-making problem (Porter, 1981 and Stevenson, 2002: 175). Long-term capacity decisions are difficult to make because they must be arrived at in the face of great uncertainty about future demand, future costs, technological change, and competitors capacity plans (Hanna and Newman, 2001: 315 and von Lanzanaeur, 2002).

Capacity planning is of critical importance to the sustenance of a business for a number of reasons (Stevenson, 2002: 175);

• Capacity decisions set the upper limit for capacity output possible thereby affecting a firms ability to meet future demand for its products and services. Decisions resulting in too much capacity under-utilise a firms resources, driving up its costs which then reduces its ability to compete. On the other hand, inadequate capacity will result in the firm failing to satisfy its customers with the added possibility of customers being lost as well as a decreased market share for the firms products. However, a firm with excess capacity may be better placed to take advantage of tremendous opportunities such as unexpected peaks in demand.
• Capacity decisions involve the choice of the production technology to be used which will directly affect the firms operating costs. In an ideal world, capacity and demand requirements ought to be matched, thus minimising operating costs. However, this is not always achieved in practice because actual demand either differs from expected demand or tends to vary (e.g. cyclically or seasonally). In such cases, a decision might be made to attempt to balance the costs of over- and under capacity.
• Capacity is usually a major determinant of the initial cost of the firm. Typically, the greater the capacity of a production unit, the greater its cost though this does not necessarily imply a one-for-one relationship as larger units tend to cost proportionately less than smaller units. This will affect the length of time required to re-coup the investment.
• Capacity decisions often involve long-term commitment of resources and the fact that once they are implemented, it may be difficult or impossible to modify those decisions without incurring major costs.
• Capacity decisions can affect competitiveness. If a firm has excess capacity, or can quickly add capacity, that fact may serve as a barrier to entry to other firms though Lieberman (1987) found the use of capacity in this manner to be rare and unlikely to be completely effective. Excess capacity can positively affect delivery speed, which can be a competitive advantage.
• Capacity affects the ease of management as having appropriate capacity makes management easier than when capacity is mismatched calling for fire-fighting, scheduling overtime, sub-contracting which all cause increased complexity. 

From the foregoing, it may be concluded that firms ought to exercise extreme care when making their capacity expansion decisions as the consequence of getting it wrong could have grave consequences for the firm. Hammesfahr et al (1993) summarises this well by stating that capacity decisions require careful analysis and consideration at the highest level of planning to provide the maximum opportunity for a manufacturer to achieve its strategic objectives since production capacity decisions for new, expanding and existing facilities impact directly on a firms competitive position and resulting profitability.

In addition, it must be noted that the firm does not exist alone in the market place thus a poor decision by one firm can often cause significant long-term losses for an entire industry since overcapacity in the industry would lead managers to discount prices so as to boost demand to utilise the capacity fully which in turn would cause price wars that would hurt the whole industry (Hanna and Newman, 2001 and Bashyam, 1996). Gilbert and Lieberman (1987) demonstrated that firms pre-empt their rivals in building plant capacity mainly as a means of signalling their presence and avoiding excess capacity in the industry.

5.3 Concepts of capacity planning

Capacity decisions are dependent on the concepts of economies of scale, the experience curve and capacity cushion.

Economies of scale

The factors that act in tandem to reduce costs as volume increases are often called economies of scale. Economies of scale are based on the notion that large units are more economical because fixed costs can be spread over more units of production (Schroeder 2000: 231, Slack and Lewis 2002: 126 and Chase et al 2001: 357). These economies occur because the cost of building and operating large production equipment does not necessarily increase linearly with volume. Hayes and Wheelwright (1984: 58) suggest that the reason for this is that whereas the capacities of much equipment is roughly related to their interior volumes (a cubic function), the capital cost of the equipment is more closely related to their surface area (a square function). They go on to define the costs associated with providing capacity in one increment of size V as;

C (V) = KV^k

where;

K = a constant scale factor dependent on the industry

k = a factor usually between 0.6 and 1.0 which indicates the degree of economies of scale

An example of where this concept is used is in the estimation of the costs of providing new capacity in production units that process liquids such as chemical reactors and oil refineries. These production units are basically cylindrical and as such their surface areas increase with the square of their radius while their volumes increase only with the cube of their radius. Therefore the cost associated with providing capacity can be defined as;

C (V) = KV

In the case when a choice has to be made between two sets of equipment with differing capacities of 10,000 tons and 20,000 tons, then the costs associated with either purchase can be calculated as;

C (10000) = K10000= 464.158 K

C (20000) = K20000= 736.806 K

It is then evident that the costs associated with buying the larger capacity equipment (which is double the capacity) is about 60% more than the cost of acquiring the smaller capacity equipment contrary to the general expectation that it ought to be twice as much.

Therefore a machine with twice the output rate will generally cost less than twice as much to buy and operate. In addition to the reduced costs of purchase and operation, larger facilities enable the overhead due to managers and staff to be spread over more units of production resulting in reduced unit costs of production. However as the facility gets larger, diseconomies of scale occur thereby increasing the unit costs as output volume increases. The diseconomies of scale arise mainly due to the greater complexity involved in managing a larger organisation since communications, coordination and control costs increase in large organisations.

Output rate (patients per week)

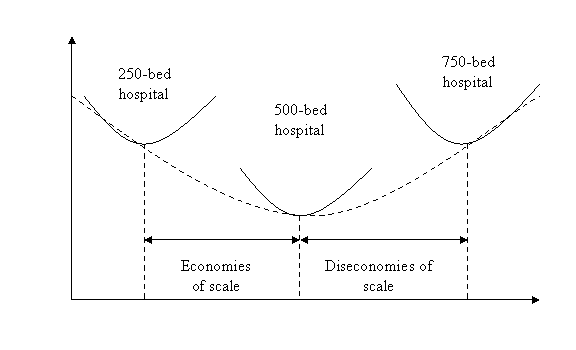
Figure Economies and Diseconomies of Scale

Source: Krajewski, L.J. and Ritzman, L.P. (2001) Operations Management: strategy and analysis (6th Edn), Prentice Hall, p333

It has been noted that a misunderstanding of the economies of scale has led a number of firms to fall into the trap of adding too many products or processes to facilities that were originally designed for other products and processes (Martinich 1997: 256). This is because economies of scale are attained by making larger volumes of the same or similar products and not necessarily by making more products that are dissimilar. Increasing output with dissimilar products calls for increased co-ordination and scheduling efforts which may result in reduced efficiency in the production of the original products. Skinner (1974) asserted that factories work best when they focus on a limited set of production objectives, thus economies of scale would work hand in hand with focused factories.

Experience Curve

The other concept to consider in sizing of capacity is the experience curve which is used to explain the phenomenon of reduced unit costs of production that plants enjoy with cumulative production. Chase et al (2001: 357) note that as plants produce more, they gain experience on the best production methods, which reduce their costs of production in a predictable manner thus enjoying the experience curve effect. The experience curve is therefore a combination of the learning curve effects of workers as they get more experienced in their jobs as well as the organisational factors such as process improvement, better management and information flows and exploitation of scale economies.

Therefore whenever a plants cumulative output doubles, its production costs decline by a specific percentage depending on the nature of the business (Chase et al 2001: 357). A plant is said to have a 90% experience curve, if the production costs required to make for instance 200 units of a product is 90% of that required to make 100 units of a product.

The production cost required to make the nth unit of the product will be;

C_n = C₁n^a

Where;

C_n = cost of making the nth unit

C₁ = cost of making the first unit

a = (ln x)/(ln 2)

x = experience rate (expressed as a decimal)

Using the above example, if the cost of making 100 units is £500 in an industry or firm that has a 90% experience rate, then with every doubling of the cumulative production the cost of production will be expected to reduce by 10%. Thus the cost of producing 200 units will be 90% of £500 which is £450, while the cost of producing 400 units will be 90% of £450 which is £405. However, if a firm wishes to find out the cost of making an intermediate value such as 300 units in order to make a quotation for a tender, then the above formula can be used as shown below;

C_n = C₁n^a

C₃₀₀ = C₁₀₀

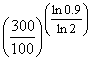
C₃₀₀ = £5000.8462 = £423.10

Chase et al (2001: 357) point out that, large firms can have a two-way cost advantage over their competitors by having both scale economies and experience curve effects. This is because the higher volumes that give rise to scale economies will in turn also trigger greater experience curve effects. Besides cost advantages, another consequence of learning and experience effects are that capacity for a given factory can increase over time without expanding the capacity infrastructure therefore such considerations should be considered when making the capacity plans of a firm (Martinich 1997: 263).

Capacity cushion

The final concept to be considered when making capacity sizing decisions is that of the capacity cushion. The capacity cushion is defined as the amount of the planned capacity that is above the forecast level of demand (Slack and Lewis 2002: 166). Since the capacity cushion is expressed relative to the forecast demand level, a positive cushion would provide excess capacity over the forecast demand while a negative cushion would imply that the forecast demand exceeds capacity (Schroeder 2000: 229).

A positive cushion would enable a firm to cope with demand greater than the forecast demand albeit with the cost of excess capacity when demand does nit reach capacity. A negative cushion would enable a firm to maximise the utilisation of its equipment thus keeping its unit costs low though it faces the risk of lost sales when demand exceeds capacity.

The ultimate decision of how much capacity cushion to have is dictated by the relative difference in the costs of having over- or under-capacity and these are specific to the industry that a firm is involved in. For instance capital-intensive industries tend to work with lower capacity cushions owing to their higher cost capacity, while less capital-intensive industries manage with higher capacity cushions (Krajewski and Ritzman 2001: 334).

5.4 Common steps in capacity planning

The following eight steps are often quoted in the literature as commonly used in capacity planning (e.g. Hayes and Wheelwright 1984: 126 and Krajewski and Ritzman 2001: 338);

• Audit and evaluate existing capacity
• Forecast capacity requirements
• Define alternatives for meeting requirements
• Perform financial analyses for each alternative
• Assess key qualitative issues for each alternative
• Select the alternative to be pursued
• Implement the chosen alternative
• Audit and review actual results

6 Elements of capacity planning

The principal driver of business strategy is customer demand thus capacity planning has to be done in the wider context of the strategic relationship between capacity and demand, specifically translated into capacity expansion or reduction strategies. The literature suggests that there are some basic issues to be considered when making capacity planning decisions (Martinich, 1997: 252, Schroeder 2000: 228, Slack and Lewis, 2002: 114 and Stevenson, 2002: 174) namely;

The nature of the capacity required

The size of the capacity required

The timing of the capacity addition

The location of the capacity addition

It is thus necessary to understand the implications of these issues on the capacity decision. Schroeder (2000: 229) assert that these elements need to be considered in an integrated fashion and are affected by the following factors:

• Predicted (forecast) demand is required to formulate a facilities strategy.
• The cost of facilities affects the choice of whether to have large or small facilities. Cost also affects the amount of capacity added at any one time, the timing and the location of capacity.
• The likely behaviour of competitors will affect the way a firm approaches the capacity expansion. An expected slow competitive response may lead a firm to add capacity in order to grab the market before competitors become strong. While on the other hand, an expected fast competitive response may cause the firm to be more cautious in expanding capacity.
• The business strategy may dictate that a firm put more emphasis on cost, service or flexibility in facilities choices. For example, a business strategy to provide the best service can lead to facilities with some excess capacity or several market locations for fast service.
• As markets become more global in nature, facilities also must be located globally. This involves not merely chasing cheap labour but locating facilities globally for the best strategic advantage.

6.1 Nature of capacity required

The nature of the capacity required is dependent on the specific industry that a business is involved in and thus it may be said that the choice of industry as well as the products or services to be produced governs the capacity planning decision (Stevenson 2002: 174). As Martinich (1997: 255) notes, a fundamental aspect of capacity decisions is whether the facilities are best organised around products (with the production of a product or product family in one facility), processes (with each facility responsible for one process in the production stage) or markets (with each facility responsible for supplying a range of products to a geographical area).

The decision of whether a firm should best configure its capacity around its products, processes or markets will be dictated by an evaluation of the production and distribution costs, as well as the range of products and geographical markets served by the firm (Martinich 1997: 255). Product-focused facilities are usually deployed when a large market exists to justify a dedicated facility coupled with the fact that the process inputs and steps required to make the product are different from those of other firm products.

Process-focused facilities are used when a variety of products can be produced economically by the use of a single production process technology. They usually produce components or parts that are shipped to other facilities for further processing or assembly and they are commonly found in the automotive industry, where engine plants and transmission plants feed the final assembly plants.

Market-focused facilities are best used when close proximity to the customer is beneficial either because customers must come to the facility or because it is important to serve customers quickly (Martinich 1997: 256). Many service operations fall into this category, since services cannot be transported while plants that require quick customer response coupled tend to be market-focused especially when faced with high transportation charges.

6.2 Size of the capacity required

A number of factors have been cited as affecting the decisions of size of capacity and they essentially fall into two categories; market requirements and operations resources (Slack and Lewis 2002: 120). These are akin to what Hill (1995: 8) refers to as the twin objectives of operations management; resource utilisation and customer service. Market requirement related issues include the level and uncertainty of forecast demand, and the consequences of having excess or insufficient capacity. The issues dictated by the operations resources include the availability of capital, the cost structure of the capital increment, the likelihood of enjoying economies of scale, the experience curve effects, the flexibility of capacity provisions, technological change in process methods and legislation change for instance with regard to environment pollution control.

Knowledge of forecast demand would enable a firm to determine the amount of capacity required as being the difference between its effective capacity and the forecast demand. However, the decision is not as simple as it would seem since by virtue of their definition, forecasts are mired with uncertainties which complicate the capacity decision. Balachandran et al (1997) summarise by stating that uncertainty in product markets makes capacity planning a difficult exercise. Therefore the critical question is whether the forecast demand in the short-run will be higher or lower than the expected long-term sustainable demand (Slack and Lewis 2002: 124). This will in turn help to determine whether the firm should build to meet long-term demand as against short-term demand.

This decision will have an impact on how profitably the firm can expect to run its plant, how efficiently it can meet customer demand and how quickly it can expect to re-coup its investment. Having excess capacity increases unit costs while increasing the flexibility of meeting short-term fluctuations in demand, whereas insufficient capacity minimises unit costs while restricting the firms ability to respond to customer demand.

The size of the capacity change is frequently determined by factors outside the control of a firm such as technical specifications on the minimum sizes of equipment. So firms may be faced with a choice of having a capacity increment that exceeds their initial requirement due to this phenomenon of lumpiness of capacity. There is thus a need to balance between the marketing requirements and the operational resource limitations given the importance of having accurate forecasts in making appropriate decisions regarding the size of investment in manufacturing capacity.

6.3 Timing of the Capacity Change

With an idea of the size of capacity required, the next consideration is when to change the capacity. Just as in the case of sizing decisions, there is general agreement that the forecast level of demand has a major influence on the timing decision (Slack and Lewis 2002: 149 and Hill 2001: 192). To an extent the timing and capacity size decision are linked due to the concept of lead time required to effect a capacity change. Krajewski and Ritzman (2001: 337) explain that if as demand increases, the time between capacity increments increases then the size of the increments must increase too in order to meet demand. Therefore firms have the choice of either increasing capacity in smaller increments over shorter periods or increasing capacity in larger increments over longer periods. The drawback with smaller increments is that they cost more per unit of output than larger increments due to the economies of scale effects. Conversely, larger increments will burden a firm with excess capacity for a longer time resulting in higher unit costs.

6.4 Location of capacity addition

It has been noted that as plants get larger, diseconomies of scale set in to increase the unit costs of production. Therefore firms have to carefully consider whether to expand on the same site or to place the new capacity on a different location altogether in order to have the optimal size. A number of factors have been identified in the literature as affecting the location decision (Slack and Lewis 2001: 131-136, Krajewski and Ritzman 2001: 408, Hill 2001: 194) and they principally relate to the accessibility to the market judged by the required customer service level and geographical distribution of demand, as well as operations resource issues such as economies of scale, proximity to suppliers and resources, and access to a favourable labour climate. Stonebraker and Leong (1994: 183) stress that the location decision should be consistent with the long-term strategic goals of the firm and not focused strictly on market and operation resource issues.

Location decisions have an impact on the financial investment requirements, operating costs and revenues, and operations. Thus a poor choice of location may result in excessive transportation costs, a shortage of qualified labour, loss of competitive advantage, inadequate supplies of raw materials, or some similar condition that is detrimental to operations (Stevenson 2002: 356).

7 Capacity strategy

There are a number of definitions of capacity strategy but they seem to have the theme of it being the end result of a series of separate capacity decisions over time. Hayes and Wheelwright (1984: 46-47) define capacity strategy as the sequence of specific capacity decisions over time while Slack and Lewis (2002: 114) define it as the pattern of decisions concerned with how operations configure and change in order to achieve a particular level of output potential.

The capacity strategy process thus involves rationalising between the cost structure and lumpiness of the capacity, the product demand pattern and the primary order-winning dimensions that the firm has chosen to distinguish itself in the market (Martinich 1997: 258). Wild (1995: 266) notes that there are two approaches to capacity management. One approach is plan capacity in order to match changing demand though this entails risks of having too much or too little capacity. The other approach is to increase or reduce demand through marketing efforts such as adverts, price changes and promotions.

The principal capacity decisions are the timing and sizing of new capacity addition in relation to demand changes (Hayes and Wheelwright 1984: 48). Two extreme strategies of building capacity ahead of demand and building capacity after demand has materialised have been noted in the literature, with some firms attempting to find the optimal strategy in between. The figure below illustrates the difference between the two strategies.

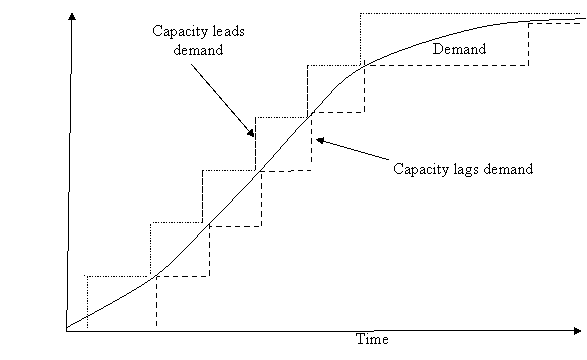
Figure Capacity leading and capacity lagging strategies

Source: Slack, N. and Lewis, M. (2002). Operations Strategy. Pearson Education, p. 150.

The demand leading strategy involves the introduction of capacity in advance of forecast demand. This gives rise to a positive capacity cushion which enables a firm to respond quickly to unexpected increases in demand thus maximising its revenues as well as its customer service. This strategy is particularly useful in rapidly growing markets (Martinich 1997: 258) or with products in their growth stage with rapidly growing sales (Krajewski and Ritzman 2001: 317). Martinich (1997: 258) notes that the viability of this strategy is dependent on the willingness of customers to postpone their purchases when their demand can not be met. Given the uncertainty of forecast demand, this strategy can result in high levels of over-capacity when the forecast demand does not materialise. The excess capacity can be very expensive thus this strategy is most appropriate in industries that do not require expensive equipment (Martinich 1997: 258).

Demand lagging strategy, also called the conservative or wait-and-see or demand cushion strategy, is centred on maximising the utilisation of existing capacity until such a time when the demand is expected to exceed the current capacity over the long-term. Martinich (1997: 258) notes that this strategy usually assumes that the firm can increase short-term capacity via overtime work or subcontracting, and/or the customers are willing to accept some delay in delivery. This results in low unit costs of production though the overtime and subcontracting costs may be substantial when demand exceeds the nominal capacity. There is also the likelihood of lost sales when customers are not willing to tolerate delays. Slack and Lewis (2002: 152) suggests that this strategy can be useful during the maturity stage of a product where the demand is relatively predictable and the main concern is to keep costs low.

Demand matching strategy attempts to find an optimal balance between the demand leading and demand lagging strategies. This strategy would be most appropriate in situations where both the level of demand and its growth rate are predictable. Failure to do this will result in either of the two extreme strategies discussed above. A variation of this strategy is smoothing with inventory stocks where capacity shortages in one period are off-set by inventory generated due to excess capacity in a previous period.

Figure Smoothing capacity with inventory

Source: Slack, N. and Lewis, M. (2002). Operations Strategy. Pearson Education, p. 151.

Demand Strategies - As earlier noted by Wild (1995), firms may also manage their capacity by controlling the demand that their systems face. Martinich (1997: 260) notes that regardless of the capacity expansion strategy used, firms will almost always benefit if they can satisfy the same total demand using less investment in capacity. He further notes that a leading cause of under-utilised capacity is short-term fluctuations in demand caused by some products being highly seasonal or cyclical in their relative demand. One approach suggested in the literature is to identify products or services that have complementary demand patterns or patterns that tend to offset each other such that the capacity is able to be fully utilised throughout the year. The ideal case is one in which products or services with complementary (counter cyclic) demand patterns involve the use of the same resources but at different times, so that the overall capacity requirements remain fairly stable (Stevenson 2002: 181).

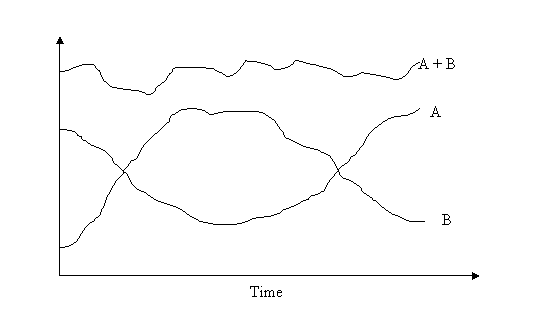
Figure Products with complementary demand patterns

Source: Stevenson, W.J. (2002). Operations Management (7th Edn). McGraw-Hill, p. 18

8 Capacity Evaluation

A firm needs to examine the alternatives for future capacity from a number of different perspectives with the most apparent one being economic considerations (Stevenson (2002: 184). As Martinich (1997: 262) observes, a major consideration in capacity decisions of all manner is the uncertainty of future demand forecasts. He suggests that tools that can include this uncertainty in the decision process can be valuable in the evaluation process.

A number of techniques are available for evaluating capacity alternatives from an economic standpoint with the most common being break-even (cost-volume) analysis and decision theory.

8.1 Break-even (cost-volume) analysis

The break-even analysis focuses on the relationships between cost, revenue and volume of output. The issues surrounding these relationships are said to be the most basic, and yet the most important, in capacity strategy (Slack and Lewis 2002: 125). The purpose of cost-volume analysis is to estimate the income of an organisation under different operating conditions and it is particularly useful as a tool for comparing capacity alternatives (Stevenson 2002: 185).

The use of this analysis requires the identification of all costs related to the production of a given product. Fixed costs are those that have to be incurred irrespective of how much the capacity is being used. They tend to remain constant and may include rent, property taxes and certain administrative costs. Variable costs of operating the capacity are those that vary directly with volume of output and the major components of variable costs are generally materials and labour costs.

Assuming that the variable cost per unit remains the same regardless of volume of output, the total cost associated with a given volume of output is equal to the sum of the fixed cost and the variable cost per unit multiplied by the volume:

TC (Total cost) = FC (Fixed cost) + VC (Variable cost)

VC = Q (Quantity or Volume of output) v (variable cost per unit)

Revenue per unit, like the variable cost per unit, is assumed to be the same regardless of quantity of output. Assuming that all output can be sold, then the total revenue associated with a given quantity of output Q is:

TR (Total revenue) = Q R (Revenue per unit)

At break-even point TR = TC which is displayed in the figure below.

Total revenue

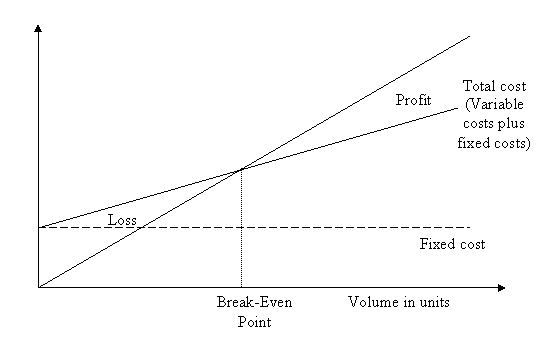
Figure Cost-volume relationships

Source: Stevenson, W.J. (2002). Operations Management (7th Edn). McGraw-Hill, p. 186

Often capacity decisions may involve the acquisition of new machines which bring in additional fixed costs and possible different variable costs. The same technique can be used though it will give rise to a situation of multiple break-even points as illustrated in the diagram below. The number of machines to be purchased will have to have a break-even point that is less than the projected annual demand otherwise the capacity will operate at a loss.

Quantity

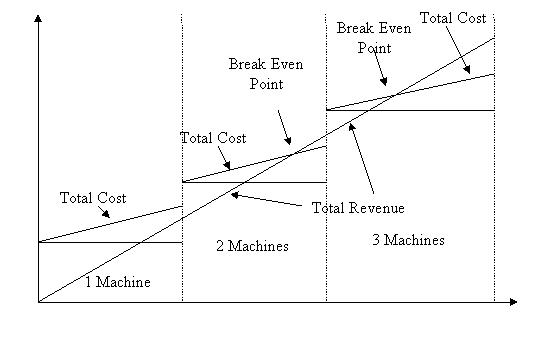
Figure Multiple break-even points

Source: Stevenson, W.J. (2002). Operations Management (7th Edn). McGraw-Hill, p. 187

Break-even analysis has a few drawbacks as it relies on the following assumptions (Stevenson 2002: 188);

1. One product is involved.
2. Everything produced can be sold.
3. The variable cost per unit is the same regardless of the volume.
4. Fixed costs do not change with volume changes or they are step changes.
5. The revenue per unit is the same regardless of volume,
6. Revenue per unit exceeds variable cost per unit.

These assumptions may not hold in real life as costs may change with time plus the separation of variable and fixed costs is not as easy as it would seem in many firms so it should be used with caution probably as an initial check on the viability of a proposal.

8.2 Decision Analysis

Decision analysis is useful when a more explicit inclusion of uncertainty than is offered by break-even analysis is required (Martinich 1997: 265). Decision analysis is thus a set of techniques used to evaluate alternative actions by considering both the probabilities and consequences of different outcomes.

To use decision analysis, decision makers would employ this process (Stevenson 2002: 197):

1. Identify the possible future conditions (e.g. demand will be low, medium or high; the number of contracts awarded will be one, two or three; the competitor will or will not introduce a new product) known as the states of nature.
2. Develop a list of possible alternatives, one of which may be to do nothing.
3. Determine or estimate the payoff associated with each alternative for every possible future condition.
4. If possible, estimate the likelihood of each possible future condition.
5. Evaluate alternatives according to some decision criterion (e.g. maximise expected profit) and select the best alternative.

Decision Environments.

The decision analysis is dependent on the degree of certainty present in the decision environment. There are two basic categories;

• Decision under Uncertainty which is when the payoffs are known but it is not possible to ascertain the likelihood of the outcomes occurring.
• Decision under Risk which is when the payoffs are known and the probability of certain outcomes are also known.

Table Payoff table

Source: Stevenson, W.J. (2002). Operations Management (7th Edn). McGraw-Hill, p. 197

Decision making under uncertainty

In the case when it is not possible to assess likelihood of certain conditions occurring, four possible decision criteria may be used to analyse the decision.

Maximin the worst possible payoff for each alternative is determined and the one with the best worst payoff is considered. This approach is a pessimistic one because it takes into account only the worst possible outcome for each alternative and tries to minimise the bad that can result. Whereas the actual outcome may not be as bad as that, this approach establishes a guaranteed minimum. So using the payoff table above, the worst payoffs for the alternatives are; Small facility 10, Medium facility 7 and Large facility (4). Hence since 10 is the best payoff, the small facility is chosen using the maximin strategy.

Maximax the best possible payoff for each alternative is determined and the one with largest payoff is selected. In contrast to the maximin strategy, the maximax is an optimistic strategy as it only considers the best outcomes. Using maximax, the best payoffs are: Small facility 10. Medium facility 12 and Large facility 16. The best overall payoff is for the large facility (16) thus the large facility is chosen using the maximax strategy.

Laplace the alternative with the best average payoff is selected and in so doing the Laplace method treats all future outcomes as equally likely. Using the Laplace method, the average payoffs are; Small facility 10, Medium facility 10.33 and Large facility 4.67. The medium facility is chosen using the Laplace method because it has the highest average.

Minimax regret the worst regret for each alternative is determined and the alternative with the best worst is chosen. This approach seeks to minimise the difference between the payoff that is realised and the best payoff for each state of nature. The lowest regret is 4 for the medium facility, hence that alternative would be chosen under minimax regret as indicated in the opportunity loss table below.

Table Opportunity Loss (Regret) table.

Source: Stevenson, W.J. (2002). Operations Management (7th Edn). McGraw-Hill, p. 197

Stevenson (2002: 200) summarises by stating that the basic weakness of these approaches (with the notable exception of Laplace) is that they do not consider all of the payoffs as they focus on either the best or the worst outcomes.

Decision making under risk

When both the payoffs and probabilities of different outcomes occurring are known, then the problem may be approached using the expected monetary value criterion with the aim of maximising the expected payoff or monetary value.

The expected value is the sum of the payoffs for an alternative where each payoff is weighted by the probability for the relevant state of nature. Thus the approach is:

EV = (probability if outcome i occurs ) x (payoff if outcome i occurs)

So if in the payoff table above the probabilities for low, moderate and high demand occurring were 0.3, 0.5 and 0.2 respectively, then the expected values would be;

EV_small = 0.3 x 10 + 0.5 x 10 + 0.2 x 10 = 10

EV_medium = 0.3 x 7 + 0.5 x 12 + 0.2 x 12 = 10.5 (HIGHEST)

EV_large = 0.3 x -4 + 0.5 x 2 + 0.2 x 16 = 3

The medium facility is chosen because it has the highest expected value.

Figure Decision Tree Analysis for Capacity Expansion Problem

8.3 Investment Analysis

Besides cost-volume analysis and decision analysis, firms often have to carry out an investment analysis in order to assess the viability of the different capacity alternatives based on the return on investment. Investment analysis involves the consideration of the amount of capital investment, the variable costs and cash flows associated with each alternative.

The net present value method is one of the best and most widely used methods of ranking investment alternatives (Heizer and Render 2003: 288). It is based on the fact that money has a time value, thus money today will not have the same value tomorrow due to factors such as inflation, interest and so on. It involves calculating the net present value of all cash flows for each investment alternative. It thus makes it possible to have a common reference point when evaluating among different alternatives, thus the investment with the highest net present value is selected.

In general, the future value of money can be calculated by the formula below;

F = P(1+i)^N

Where;

F = future value

P = present value

i = interest rate

N = number of years

However, since the decision makers are mostly interested in finding out the present values of a series of future cash receipts then this formula can be solved for P as shown below;

P =

However when N becomes large the computation becomes cumbersome and interest tables such as the one below can be particularly helpful.

Thus P = F X where X = a factor from the interest table below

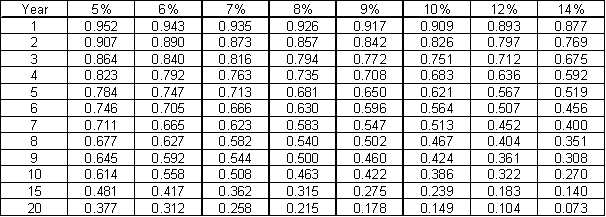
Table Present Value Table

Example

Quality Plastics, Inc. is considering two different investment alternatives. Investment A has an initial cost of £25,000 and investment B has an initial cost of £26,000. Both investments have a useful life of 4 years. The cash flows for these investments are as indicated in the table below with the cost of capital (i) at 8%.

To find the present value of the cash flows for each investment, the present value factors are multiplied by the cash flow for each investment for each year. The sum of these present value calculations minus the initial investment is the net present value of each investment.

The net present value criterion shows investment B to be more attractive than investment A because it has a higher net present value.

Heizer and Render (2003: 289) point that even though the net present value is one of the best approaches to evaluating investment alternatives, it does have some limitations which include the following:

1. Investments with the same net present value may have significantly different projected lives and different salvage values.
2. Investments with the same net present values may have different cash flows. These differences in the cash flows may have a substantial effect on the firms ability to pay its bills.
3. The assumption is that we know future interest rates, which we do not.
4. Payments are always made at the end of the period (week, month or year), which is not always the case.

9 Conclusion

Strategic capacity planning decisions which determine the size of capacity, timing of capacity addition, the nature of the capacity and its location need to be carefully considered as they have a great impact on the way a firm will operate as well as its profitability. They require a simultaneous consideration of market requirements as well as operations resource issues in order to come up with an equitable balance between the twin objectives of operations management resource utilisation and customer service.