| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
INTRODUCTION TO RATIO ANALYSIS
Ratio Analysis
Ratio analysis is the assessment of the proportionate relationship, in time and amplitude, of one wave to another. In discerning the working of the Golden Ratio in the five up and three down movement of the stock market cycle, one might anticipate that on completion of any bull phase, the ensuing correction would be three-fifths of the previous rise in both time and amplitude. Such simplicity is seldom seen. However, the underlying tendency of the market to conform to relationships suggested by the Golden Ratio is always present and helps generate the right look for each wave.
The study of wave amplitude relationships in the stock market can often lead to such startling discoveries that some Elliott Wave practitioners have become almost obsessive about its importance. Although Fibonacci time ratios are far less common, years of plotting the averages have convinced the authors that the amplitude (measured either arithmetically or in percentage terms) of virtually every wave is related to the amplitude of an adjacent, alternate and/or component wave by one of the ratios between Fibonacci numbers. However, we shall endeavor to present the evidence and let it stand or fall on its own merit.
The first evidence we found of the application of time and amplitude ratios in the stock market comes from, of all suitable sources, the works of the great Dow Theorist, Robert Rhea. In 1936, Rhea, in his book The Story of the Averages, compiled a consolidated summary of market data covering nine Dow Theory bull markets and nine bear markets spanning a thirty-six year time period from 1896 to 1932. He had this to say about why he felt it was necessary to present the data despite the fact that no use for it was immediately apparent:
Whether or not [this review of the averages] has contributed anything to the sum total of financial history, I feel certain that the statistical data presented will save other students many months of work. Consequently, it seemed best to record all the statistical data we had collected rather than merely that portion which appeared to be useful. The figures presented under this heading probably have little value as a factor in estimating the probable extent of future movements; nevertheless, as a part of a general study of the averages, the treatment is worthy of consideration.
One of the observations was this one:
The footings of the tabulation shown above (considering only the industrial average) show that the nine bull and bear markets covered in this review extended over 13,115 calendar days. Bull markets were in progress 8,143 days, while the remaining 4,972 days were in bear markets. The relationship between these figures tends to show that bear markets run 61.1 percent of the time required for bull periods.
And finally,
Column 1 shows the sum of all primary movements in each bull (or bear) market. It is obvious that such a figure is considerably greater than the net difference between the highest and lowest figures of any bull market. For example, the bull market discussed in Chapter II started (for Industrials) at 29.64 and ended at 76.04, and the difference, or net advance, was 46.40 points. Now this advance was staged in four primary swings of 14.44, 17.33, 18.97, and 24.48 points respectively. The sum of these advances is 75.22, which is the figure shown in Column 1. If the net advance, 46.40, is divided into the sum of advances, 75.22, the result is , which gives the percent shown in Column 1. Assume that two investors were infallible in their market operations, and that one bought stocks at the low point of the bull market and retained them until the high day of that market before selling. Call his gain 100 percent. Now assume that the other investor bought at the bottom, sold out at the top of each primary swing, and repurchased the same stocks at the bottom of each secondary reaction his profit would be , compared with 100 realized by the first investor. Thus the total of secondary reactions retraced percent of the net advance. [Emphasis added.]
So in 1936 Robert Rhea discovered, without knowing it, the Fibonacci ratio and its function relating bull phases to bear in both time and amplitude. Fortunately, he felt that there was value in presenting data that had no immediate practical utility, but that might be useful at some future date. Similarly, we feel that there is much to learn on the ratio front and our introduction, which merely scratches the surface, could be valuable in leading some future analyst to answer questions we have not even thought to ask.
Ratio analysis has revealed a number of precise price relationships that occur often among waves. There are two categories of relationships: retracements and multiples.
Retracements
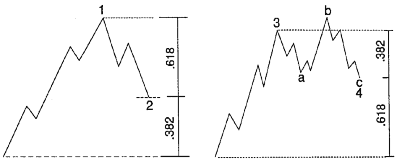
Occasionally, a correction retraces a Fibonacci percentage of the preceding wave. As illustrated in Figure 4-1, sharp corrections tend more often to retrace 61.8% or 50% of the previous wave, particularly when they occur as wave 2 of an impulse wave, wave B of a larger zigzag, or wave X in a multiple zigzag. Sideways corrections tend more often to retrace 38.2% of the previous impulse wave, particularly when they occur as wave 4, as shown in Figure 4-2.
|
Figure 4-1 |
Figure 4-2 |
Retracements come in all sizes. The ratios shown in Figures 4-1 and 4-2 are merely tendencies, yet that is where most analysts place an inordinate focus because measuring retracements is easy. Far more precise and reliable, however, are relationships between alternate waves, or lengths unfolding in the same direction, as explained in the next section.
Lesson 21: Motive and Corrective Wave Multiples
WAVE MULTIPLES
Motive Wave Multiples
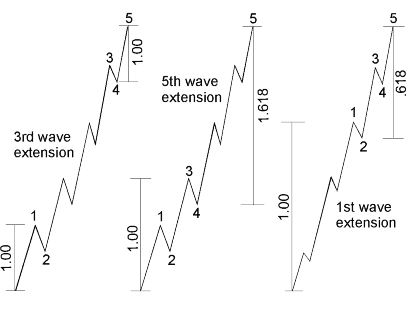
Lesson 12 mentioned that when wave 3 is extended, waves 1 and 5 tend towards equality or a .618 relationship, as illustrated in Figure 4-3. Actually, all three motive waves tend to be related by Fibonacci mathematics, whether by equality, 1.618 or 2.618 (whose inverses are .618 and .382). These impulse wave relationships usually occur in percentage terms. For instance, wave I from 1932 to 1937 gained 371.6%, while wave III from 1942 to 1966 gained 971.7%, or 2.618 times as much. Semilog scale is required to reveal these relationships. Of course, at small degrees, arithmetic and percentage scales produce essentially the same result, so that the number of points in each impulse wave reveals the same multiples.
|
Figure 4-3 |
Figure 4-4 |
Figure 4-5 |
Another typical development is that wave 5's length is sometimes related by the Fibonacci ratio to the length of wave 1 through wave 3, as illustrated in Figure 4-4, which illustrates the point with an extended fifth wave. .382 and .618 relationships occur when wave five is not extended. In those rare cases when wave 1 is extended, it is wave 2, quite reasonably, that often subdivides the entire impulse wave into the Golden Section, as shown in Figure 4-5.
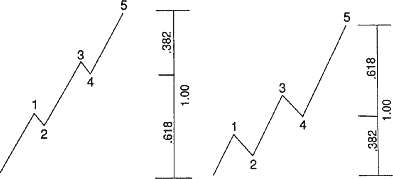
As a generalization that
subsumes some of the observations we have already made, unless wave 1 is
extended, wave 4 often divides the price range of an impulse wave into the
Golden Section. In such cases, the latter portion is .382 of the total distance
when wave 5 is not extended, as shown in Figure 4-6,
and .618 when it is, as shown in Figure 4-7. This guideline is somewhat loose
in that the exact point within wave 4 that effects the subdivision varies. It
can be its start, end or extreme counter-trend point. Thus, it provides,
depending on the circumstances, two or three closely-clustered targets for the
end of wave 5. This
guideline explains why the target for a retracement following a fifth wave
often is doubly indicated by the end of the preceding fourth wave and the .382
retracement point.
|
Figure 4-6 |
Figure 4-7 |
Corrective Wave Multiples
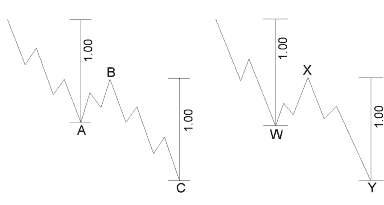
In a zigzag, the length of wave C is usually equal to that of wave A, as shown in Figure 4-8, although it is not uncommonly 1.618 or .618 times the length of wave A. This same relationship applies to a second zigzag relative to the first in a double zigzag pattern, as shown in Figure 4-9.
|
Figure 4-8 |
Figure 4-9 |
In a regular flat correction, waves A, B and C are, of course, approximately equal, as shown in Figure 4-10. In an expanded flat correction, wave C is often 1.618 times the length of wave A. Sometimes wave C will terminate beyond the end of wave A by .618 times the length of wave A. Both of these tendencies are illustrated in Figure 4-11. In rare cases, wave C is 2.618 times the length of wave A. Wave B in an expanded flat is sometimes 1.236 or 1.382 times the length of wave A.
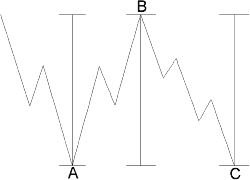
Figure 4-10
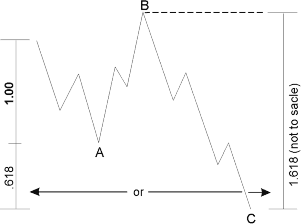
Figure 4-11
In a triangle, we have found that at least two of the alternate waves are typically related to each other by .618. I.e., in a contracting, ascending or descending triangle, wave e = .618c, wave c = .618a, or wave d = .618b. In an expanding triangle, the multiple is 1.618. In rare cases, adjacent waves are related by these ratios.
In double and triple corrections, the net travel of one simple pattern is sometimes related to another by equality or, particularly if one of the threes is a triangle, by .618.
Finally, wave 4 quite commonly spans a gross and/or net price range that has an equality or Fibonacci relationship to its corresponding wave 2. As with impulse waves, these relationships usually occur in percentage terms.
Lesson 22: APPLIED RATIO ANALYSIS
Elliott himself, a few years after Rhea's book, was the first to realize the applicability of ratio analysis. He noted that the number of DJIA points between 1921 and 1926, encompassing the first through third waves, was 61.8% of the number of points in the fifth wave from 1926 to 1928 (1928 is the orthodox top of the bull market according to Elliott). Exactly the same relationship occurred again in the five waves up from 1932 to 1937.
A. Hamilton Bolton, in the 1957 Elliott Wave Supplement to the Bank Credit Analyst, gave this price forecast based on expectations of typical wave behavior:
The powerhouse that will be building up if the market consolidates for another year or so along orthodox lines, it seems to us, will offer the probability that Primary V could be quite sensational, taking the DJIA to 1000 or more in the early 1960s in a wave of great speculation.
Then, in The Elliott
Wave Principle A Critical Appraisal, reflecting
on examples cited by Elliott,
Should the 1949 market to date adhere to this formula, then the advance from 1949 to 1956 (361 points in the DJIA) should be completed when 583 points (161.8% of 361 points) have been added to the 1957 low of 416, or a total of 999 DJIA. Alternatively, 361 over 416 would call for 777 in the DJIA.
Later, when
Since we are now well past the 777 level, it looks as if 1000 in the averages could be our next target.
The year 1966 proved those statements to be the most
accurate prediction in stock market history, when the 3:00 p.m. hourly reading
on February 9th registered a high at 995.82 (the 'intraday' high was
1001.11). Six years prior to the event, then,
Despite this remarkable portent, it was
The authors themselves have used ratio analysis, often with
satisfying success. A.J. Frost became convinced of his ability to recognize
turning points by catching the 'Cuban crisis' low in October 1962 the
hour it occurred and telegraphing his conclusion to Hamilton Bolton in
Ratio analysis has value at smaller degrees as well. In the summer of 1976, in a published report for Merrill Lynch, Robert Prechter identified the fourth wave then in progress as a rare expanding triangle, and in October used the 1.618 ratio to determine the maximum expected low for the eight month pattern to be 922 on the Dow. The low occurred five weeks later at 920.63 at 11:00 on November 11, launching the year-end fifth wave rally.
In October 1977, five months in advance, Mr. Prechter computed a probable level for the 1978 major bottom as '744 or slightly lower.' On March 1, 1978, at 11:00, the Dow registered its low at exactly 740.30. A follow-up report published two weeks after the bottom reaffirmed the importance of the 740 level, noting that:
the 740 area marks the point at which the 1977-78 correction, in terms of Dow points, is exactly .618 times the length of the entire bull market rise from 1974 to 1976. Mathematically we can state that 1022 - (1022-572).618 = 744 (or using the orthodox high on December 31st, 1005 - (1005-572).618 = 737). Second, the 740 area marks the point at which the 1977-78 correction is exactly 2.618 times the length of the preceding correction in 1975 from July to October, so that 1005 - (885-784)2.618 = 742. Third, in relating the target to the internal components of the decline, we find that the length of wave C = 2.618 times the length of wave A if wave C bottoms at 746. Even the wave factors as researched in the April 1977 report mark 740 as a likely level for a turn. At this juncture then, the wave count is compelling, the market appears to be stabilizing, and the last acceptable Fibonacci target level under the Cycle dimension bull market thesis has been reached at 740.30 on March 1st. It is at such times that the market, in Elliott terms, must 'make it or break it.'
The three charts from that report are reproduced here as Figures 4-12 (with a few extra markings to condense comments from the text), 4-13 and 4-14. They illustrate the wave structure into the recent low from Primary down to Minuette degree. Even at this early date, 740.30 seems to be firmly established as the low of Primary wave [2] in Cycle wave V.
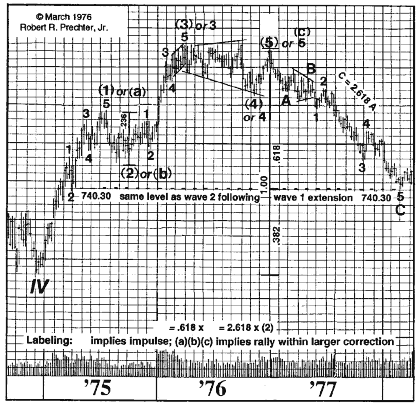
Figure 4-12
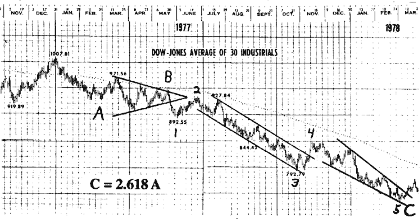
Figure 4-13
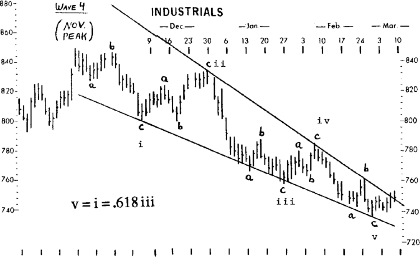
Figure 4-14
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1550
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved