| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
In varful O al
unui dreptunghi de laturi a, 2a sunt aplicate cinci forte concurente ale
caror module sunt proportionale (coeficient![]() ) cu lungimile segmentelor pe care actioneaza.
Sa se determine rezultanta sistemului de forte si ecuatia
suportului sau. Punctele M si N sunt considerate la
mijlocul laturilor respective. Caz particular:
) cu lungimile segmentelor pe care actioneaza.
Sa se determine rezultanta sistemului de forte si ecuatia
suportului sau. Punctele M si N sunt considerate la
mijlocul laturilor respective. Caz particular: ![]() , a = 2 (fig. 1.1).
, a = 2 (fig. 1.1).
|
|
R. Tinand seama ca fortele sunt proportionale cu segmentele pe care actioneaza, rezulta:
|
|
Fig. 1.1 |
Daca axele Ox si Oy sunt orientate dupa laturile dreptunghiului, componentele rezultantei sunt
X = ![]() = 2 k0 a +
= 2 k0 a + ![]() k0 a
k0 a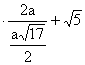 k0 a
k0 a![]() = 7 k0 a.
= 7 k0 a.
Y
= ![]() =
=![]() k0a
k0a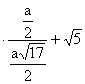 k0a
k0a![]() + k0a =
+ k0a = ![]() k0a.
k0a.
Din expresia vectoriala ![]() k0a
k0a![]() deducem modulul R =
deducem modulul R =![]() k0a si ecuatia suportului rezultantei y
=
k0a si ecuatia suportului rezultantei y
= ![]() x, z = 0
x, z = 0 ![]()
![]() x, z = 0.
x, z = 0.
In cazul particular: k0
= ![]() , a = 2, se obtine X = 2, Y = 1,
, a = 2, se obtine X = 2, Y = 1, ![]() , R =
, R = ![]() .
.
Patru forte concurente avand marimile F1 = P, F2 = F3 = 2P, F4 = 4P sunt situate in acelasi plan (fig. 1.2). Sa se determine:
a) o forta ![]() concurenta cu
cele patru forte astfel incat rezultanta lor sa fie nula;
concurenta cu
cele patru forte astfel incat rezultanta lor sa fie nula;
b) alte doua forte ![]() ,
, ![]() care sa fie
concurente cu cele patru forte si sa aiba directiile
fata de orizontala date de unghiurile
care sa fie
concurente cu cele patru forte si sa aiba directiile
fata de orizontala date de unghiurile ![]() = 45 ,
= 45 , ![]() = 135 , astfel ca sistemul sa se
reduca la
= 135 , astfel ca sistemul sa se
reduca la ![]() .
.
R. a) Alegand sistemul de axe, vom exprima mai intai proiectiile rezultantei fortelor concurente
X =![]() = 2P
= 2P![]() +2P
+2P![]() 4P
4P![]() + X5 = P
+ X5 = P![]() + X5
+ X5
Y =![]() = P + 2P
= P + 2P![]() 2P
2P![]()
![]() P
P![]() +Y5 = P
+Y5 = P![]() + Y5 ,
+ Y5 ,
|
|
de unde deducem
Pentru ca rezultanta sa fie nula, trebuie indeplinite conditiile P din care rezulta componentele fortei X5 = - P si unghiul j pe care-l face suportul sau cu axa Ox j = arctg |
|
Fig. 1.2 |
b) Procedand asemanator, vom obtine in acest caz
X =
P![]() +
+ ![]() cos 45
cos 45 ![]() cos 45
cos 45
Y =
P![]() +
+ ![]() sin 45 +
sin 45 +![]() sin 45
sin 45
Vectorul rezultantei
![]()
![]() .
.
va fi identic cu vectorul impus; rezulta conditiile
P = P![]() +
+ ![]() cos 45
cos 45 ![]() cos 45
cos 45
P = P![]() +
+ ![]() sin 45 +
sin 45 + ![]() sin 45
sin 45
din care se deduce
![]() = P
= P![]() ,
, ![]() = P
= P![]() .
.
Intr-un cerc de
raza a actioneaza
fortele concurente![]() ,
, ![]() ,
, ![]() ,
, ![]() cu
intensitati numeric egale cu segmentele pe care sunt aplicate.
Sa se determine rezultanta lor (fig. 1.3).
cu
intensitati numeric egale cu segmentele pe care sunt aplicate.
Sa se determine rezultanta lor (fig. 1.3).
|
|
R. Vom exprima mai intai marimile fortelor concurente ce actioneaza in punctul O: F1 = a Determinand expresiile vectoriale ale fortelor componente obtinem rezultanta |
|
Fig. 1.3 |
intensitatea R = ![]() si ecuatia
suportului ei: y =
si ecuatia
suportului ei: y = ![]() x, z = 0,
x, z = 0, ![]() .
.
In varful O
al piramidei OABC actioneaza fortele concurente ![]() ,
, ![]() ,
, ![]() ,
, ![]() , de intensitati proportionale cu laturile pe
care sunt aplicate, la care se adauga o forta
, de intensitati proportionale cu laturile pe
care sunt aplicate, la care se adauga o forta ![]() ce coincide cu proiectia vectorului
ce coincide cu proiectia vectorului![]() in planul orizontal. Cunoscand OB = AB = BC
= a, AM = MC si coeficientul k0, sa
se determine rezultanta sistemului de forte (fig. 1.4). Aplicatie:
in planul orizontal. Cunoscand OB = AB = BC
= a, AM = MC si coeficientul k0, sa
se determine rezultanta sistemului de forte (fig. 1.4). Aplicatie:![]() .
.
R. Alegand reperul ortogonal Oxyz, vom putea determina proiectiile
X
=![]() = F3
= F3![]() + 2 F5
+ 2 F5![]() ,
,
Y
=![]() = F1
= F1![]() + 2 F5
+ 2 F5![]() ,
,
Z =![]() = F1
= F1![]() + F2 + F3
+ F2 + F3![]() + F4
+ F4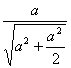 ,
,
|
|
in care F1 = k0 OA = k0a F2 = k0 OB = k0a F3 = k0 OC = k0a F4 = k0 OM = k0 a F5 = F4 cosa = k0 a |
|
Fig. 1.4 |
Dupa substituirea marimilor acestor forte, se obtin componentele
X = 2 k0a, Y = 2 k0a, Z = 4 k0a,
expresia analitica
![]() = 2 k0 a
= 2 k0 a ![]()
si modulul rezultantei
R =![]() = 2 k0 a
= 2 k0 a![]() .
.
Pentru scrierea ecuatiei suportului rezultantei, vom determina mai intai directia, calculand unghiurile formate cu cele trei axe
cos a = ![]()
cos b = ![]()
![]() .
.
Ecuatia suportului are forma generala
![]() ,
,
in care vom introduce cos a, cos b, cos si x0 = y0 = z0 = 0. In final, se obtine in planul bisector ecuatia unei drepte inclinate fata de Oz cu unghiul
= arc cos![]() ,
, ![]() .
.
Pentru cazul particular, obtinem: ![]() = 2
= 2 ![]() , R =
, R = ![]() .
.
Sa se calculeze rezultanta fortelor
concurente ale caror module sunt ![]() = 2P
= 2P![]() ,
, ![]() = = P
= = P![]() ,
, ![]() = 3P,
= 3P, ![]() = P
= P![]() (fig. 1.5). Fortele
(fig. 1.5). Fortele ![]() si
si ![]() actioneaza in planul xOy, forta
actioneaza in planul xOy, forta ![]() in planul yOz
iar forta
in planul yOz
iar forta ![]() in planul xOz.
in planul xOz.
R. Proiectiile rezultantei pe axe vor fi
X =![]() = 2P
= 2P![]()
![]() + P
+ P![]()
![]() + P
+ P![]()
![]() =
= ![]() P
P
|
|
Y = = Z
= = Putem scrie mai departe expresia vectoriala a rezultantei de unde deducem modulul |
|
Fig.1.5 |
si directia data de urmatoarele cosinusuri directoare
cos![]()
cos![]()
![]() .
.
Ecuatia suportului rezultantei va fi:
![]() .
.
Prin varful A
al unui paralelipiped trec cinci forte concurente ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() de module
de module ![]() = 4P,
= 4P, ![]() = P
= P![]() ,
, ![]() = 3P,
= 3P, ![]() = 2P,
= 2P, ![]() = P
= P![]() si de directii cunoscute. Sa se determine
rezultanta fortelor si punctele de intersectie ale suportului
sau cu fetele paralelipipedului.
si de directii cunoscute. Sa se determine
rezultanta fortelor si punctele de intersectie ale suportului
sau cu fetele paralelipipedului.
Se da: AB = BC = 2a, OC = a (fig. 1.6).
R. Proiectiile rezultantei![]() a sistemului de forte concurente pe axele Ox, Oy,
Oz sunt:
a sistemului de forte concurente pe axele Ox, Oy,
Oz sunt:
|
|
X = = 4P - P Y = = - P Z = = 3P |
|
Fig. 1.6 |
Pornind de aici se determina expresia analitica si modulul rezultantei:
![]() ,
, ![]()
In continuare vom determina ecuatiile suportului rezultantei
![]() ,
,
in care vom inlocui coordonatele punctului A: xA = 2a, yA = 2a, zA = a si cosinusurile directoare
cos a = ![]()
cos b = ![]()
cos = ![]() ;
;
rezulta ecuatiile ![]() .
.
Facand z = 0, se obtine
punctul de intersectie al dreptei cu planul Oxy: I1![]() . Asemanator se determina in Oyz
si Oxz celelalte doua puncte necesare reprezentarii
rezultantei: I2
. Asemanator se determina in Oyz
si Oxz celelalte doua puncte necesare reprezentarii
rezultantei: I2![]() , I3
, I3![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5349
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved