Forte de presiune ale fluidelor in repaus pe suprafete plane

Forte de presiune ale fluidelor in repaus pe suprafete plane

Ecuatii generale

Pentru o suprafata plana     este constanta, fortele de presiune sunt paralele,

deci rezultanta este o forta normala la suprafata plana si orientata de la fluid catre suprafata. Punctul de aplicatie al fortei se numeste centru de presiune, notat C. Pozitia centrului de presiune este data de vectorul de pozitie:

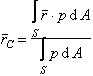. (4.4)

Actiunea unui fluid usor in echilibru static pe o suprafata plana

In capitolul 3 s-a demonstrat ca pentru un fluid usor se poate considera presiunea ca fiind constanta in intreg domeniul ocupat de fluid.

Se obtine forta de presiune rezultanta:

. (4.5)

Deci rezultanta este o forta normala pe suprafata, orientata dinspre fluid spre suprafata si egala in modul cu produsul dintre presiune si aria suprafetei plane.

Centrul de presiune se obtine din ecuatia (4.4):

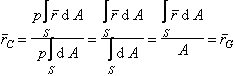. (4.6)

Deoarece numaratorul este chiar momentul static al suprafetei plane in raport cu originea, centrul de presiune coincide cu centrul de greutate (centrul de masa) al suprafetei plane respective.

Actiunea unui fluid greu in echilibru static asupra unei suprafete plane

Se alege sistemul axelor de coordonate astfel: axa Ox la intersectia dintre planul suprafetei libere a lichidului cu un plan ce contine suprafata data, iar axa Oy la intersectia dintre planul suprafetei date si un plan vertical perpendicular pe axa Ox, (fig. 4.1). Deci axa Oy se afla pe linia de cea mai mare panta a suprafetei date.

In figura 4.1 s-a reprezentat atat o sectiune in plan vertical cat si o proiectie in planul desenului a suprafetei date, avand axa Ox rabatuta.

Forta de presiune a unui lichid in repaus pe o suprafata plana este orientata de la fluid spre suprafata si este egala, in modul, cu produsul dintre aria suprafetei plane si presiunea in centrul de masa:

. (4.7)

Coordonatele centrului de presiune se obtin din coordonatele centrului de masa la care se adauga cate o excentricitate e_x, respectiv e_y

(4.8), (4.9)

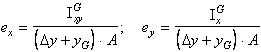, (4.10), (4.11)

unde Dy este o modificare a nivelului planului suprafetei libere a lichidului cu o inaltime egala cu inaltimea piezometrica datorata presiunii relative p_r (poate fi inaltare sau coborare dupa cum p_r este pozitiva-suprapresiune sau negativa-depresiune).

Se disting doua cazuri particulare mai importante.

Daca suprafata plana data admite o axa de simetrie verticala, aceasta se ia ca axa Oy, momentul de inertie centrifugal este zero, iar centrul de presiune se afla pe aceasta axa. Epura distributiei presiunii in sectiunea suprafetei plane date poate fi un trapez sau un triunghi. Se poate demonstra ca adancimea centrului de greutate al acestei epure coincide cu adancimea centrului de presiune. Astfel, in cazul particular al unui stavilar dreptunghiular, centrul de presiune se afla la o treime de baza.

Daca suprafata este orizontala, presiunea este constanta, iar centrul de presiune coincide cu centrul de greutate, la fel ca in cazul fluidelor usoare.

Cazuri practice sunt: calculul fortei de presiune pe un stavilar plan (fig. 4.2), un capac plan vertical sau un capac plan orizontal (fig. 4.3).