GRINZI CU ZABRELE

Aplicand metoda izolarii nodurilor, sa se determine eforturile din barele grinzii cu zabrele (fig.1a).

R. Cum grinda este constituita din b = 7 bare si n = 5 noduri., sistemul articulat este static determinat deoarece b = 2n - 3. Considerand fortele H₀, V₀, N din legaturile exterioare, se scriu ecuatiile de echilibru pentru intreaga grinda

P - H = 0, - V + N - P = 0, N 2a - P a - P 2a = 0,

si se obtine

H = P, V = , N = P.

Presupunand ca barele sunt supuse la intindere, nodul 1 (fig.1b).este actionat de forta N si de tensiunile din bare. Din ecuatiile de echilibru

T + = 0, +P = 0,

se obtine T₁₂ = , T₁₃ =. Bara 1 - 2 este comprimata iar 1 - 3 este intinsa.

Asupra nodului 2 actioneaza fortele exterioare si tensiunile din bare (fig.1c).

Ecuatiile de proiectie sunt:

P + - = 0, P + T₂₃ + + = 0 T₂₃ = P, T₂₄ = - .

Nodul 3 (fig.1d):

T - T₃₄ - T₃₅ = 0, T₃₂ - T₃₅ = 0 T₃₄ = , T₃₅ = .

Nodul 4 (fig.1e): T₄₃ + T₄₂ = 0, T₄₅ - T₄₂ = 0 T₄₅ = - .

Prima ecuatie de echilibru a nodului 4 constituie impreuna cu ecuatiile corespunzatoare ultimului nod (fig.1f) trei relatii de verificare:

+ = 0, - H + T₅₃ = 0, T₅₄ + T₅₃ -V = 0.

Sa se calculeze eforturile in barele grinzii cu zabrele din problema precedenta, utilizand metoda sectiunilor.

R. Din ecuatiile de echilibru ale grinzii rezulta H = P, V = , N = P.

Se traseaza o sectiune care intersecteaza barele 1 - 3, 2 - 3 si 2 - 4 (fig.2a) si se introduc apoi eforturile din bare, in ipoteza unor bare supuse la intindere. Pentru a calcula tensiunea T₁₃ se scrie o ecuatie de momente in nodul 2 ca punct de intersectie al tensiunilor T₂₃ si T₂₄:

T a - = 0 T₁₃ =

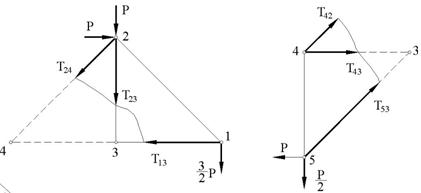
Fig.2a Fig.2b

Ecuatia de momente in nodul 3:a - Pa + T₂₄ = 0 T₂₄ = - .

Din ecuatia de momente in 4: a - T₂₃ a - Pa - Pa = 0 se obtine efortul T₂₃ = P .

Pentru a calcula tensiunile din barele 2 - 4, 3 - 4, 3 - 5 se traseaza o noua sectiune (fig.2b) si se stabilesc ecuatii de momente fata de 3, 4 si o ecuatie de proiectie pe normala la bara 3 - 5:

T + Pa - a = 0, T₅₃ + Pa = 0, - T₄₃ + - = 0;

rezulta T₄₂ = - , T₅₃ =, T₄₃ = .

Se considera o grinda articulata in A si rezemata in B (fig.3a).. Sa se calculeze eforturile din bare aplicand metoda izolarii nodurilor

R. Se verifica mai intai daca grinda cu zabrele este un sistem static determinat. Intr-adevar: b = 7, n = 5 7 = 2

Reactiunile H, V si N in legaturile exterioare se determina din ecuatiile de echilibru pentru intreaga grinda:

N - H = 0, V - 3P = 0, Na - Pa - 2P 2a = 0 H = 5P, V = 3P, N = 5P.

Din ecuatiile de echilibru ale nodului 1 (fig.3b): T₁₃ + = 0, +2P = 0, obtinem

T₁₂ = , T₁₃ = 2P.

La nodul 2 (fig.3c) apar alte doua tensiuni T₂₃ = 3P, T₂₄ = -2P , ce rezulta din ecuatiile

T₂₄ - = 0, T₂₃ + - P = 0.

Nodul 3 (fig.3d): T₃₁ - T₃₅ - = 0, T₂₃ + = 0 T₃₄ = , T₃₅ = 5P.

Nodul 4 (fig.3e). N + T₄₂ + = 0, T₄₅ + = 0 T₄₅ = 3P

Din ecuatia a doua se obtine tensiunea T₄₅ = 3P (intindere). Prima ecuatie de echilibru a nodului 4 si cele doua conditii de echilibru ale fortelor si eforturilor din ultimul nod sunt relatii de verificare

5P - 2P + = 0

T - H = 5P - 5P = 0

V - T₅₄ = 3P - 3P = 0.

Sa se determine eforturile in barele grinzii cu zabrele din problema precedenta prin metoda sectiunilor.

R. Reactiunile din articulatia A si din reazemul B (fig.4a) sunt: H = N = 5P,V = 3P.

Prima sectiune va intersecta barele 1 - 3, 2 - 3 si 2 - 4 (fig.4a). Pentru partea dreapta a grinzii, tensiunea T₁₃ se obtine din ecuatia de momente in raport cu nodul 2 de intersectie al tensiunilor T₂₃ si T₂₄, adica T₁₃ a - 2P a = 0 T₁₃ = 2P

Din ecuatia de momente in nodul 3: T₂₄ a + 2P a = 0 rezulta T₂₄ = - 2P. Cum T₁₃ si T₂₄ sunt paralele, efortul T₂₃ se va obtine din ecuatia de proiectie T₂₃ - P - 2P = 0 T₂₃ = 3P

Pentru calculul eforturilor din barele 3 - 5 si 3 - 4 se traseaza o alta sectiune care va intalni bara 2 - 4 (fig.4b). Ecuatia de momente in nodul 4: T₃₅ a - 5P a = 0 conduce la T₃₅ = 5P, iar din ecuatia de proiectie pe verticala + 3P = 0 se deduce T₃₄ =

Ecuatia de momente in nodul 3 constituie o ecuatie de verificare a calculului:

T a + 5P a - 3P a = - 2P a + 5P a - 3P a = 0.

Sa se calculeze prin metoda sectiunilor tensiunile din barele grinzii cu zabrele (fig.5a), R. Se determina mai intai fortele din legaturile exterioare.

Din ecuatiile generale de echilibru

Fig.5b Fig.5c

Celelalte tensiuni se pot determina sectionand din nou grinda (fig.5c). Din ecuatiile de echilibru

,

,

;

rezulta

,, .