NOTIUNI DESPRE TEORIA MECANISMELOR

NOTIUNI DESPRE TEORIA MECANISMELOR

1 Elementul cinematic

Organul de masina sau organele de masini care formeaza un rigid mobil se numesc elemente cinematice. Marea varietate a formelor constructive ale organelor de masini cu rol de element cinematic a dus la schematizarea lor (Fig.20) prin segmente de dreapta sau figuri geometrice poligonale nedeformabile.

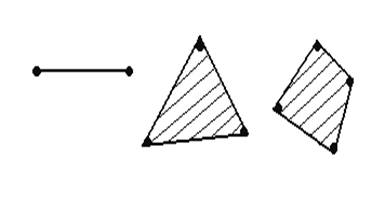
Fig.20 Schematizarea elementelor cinematice

2 Cupla cinematica

Zona sau zonele de contact dintre doua elemente cinematice, care determina posibilitatile de miscare ale celor doua elemente, se numeste cupla cinematica. Constructia acestor cuple determina ce miscari sunt permise elementelor in contact unele fata de altele.

Daca se noteaza cu f numarul miscarilor relative permise de o cupla (gradul de libertate) si cu k numarul de miscari relative blocate intyre acestea exista relatia:

F=k=6

sau

k=6-f

in virtutea faptului ca numarul de miscari independente ce le poate avea un element cinematic fata de un altul de care nu se atinge este de 6, adica trei miscari de translatie in lungul axelor unui sistem triortogonal si trei miscari de rotatie in jurul acelorasi axe. De aici rezulta foarte clar ca numarul de miscari permise de o cupla insumat cu numarul de constringeri trebuie sa fie egal cu sase.

Dupa numarul constringerilor introduse, cuplele cinematice se impart in cinci clase:

Cupla de clasa I-a

Bila ce se poate rostogoli cu alunecare pe o placa (Fig. 21):

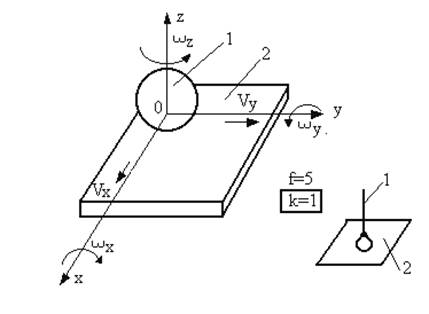
Fig.21 Cupla de clasa I

Aceasta cupla introduce o singura constringere k=1, cea de translatie pe directia 0z (v_z=0).

Cupla de clasa II-a

Este cilindrul ce se poate rostogoli cu alunecare pe o placa (Fig.22)

Constringerile introduse de aceasta cupla sunt rotirea pe axa 0x (w_x=0) si translatia dupa 0z (V_z=0) deci k=2.

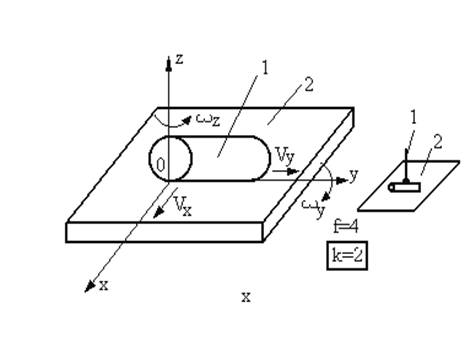
Fig.22 Cupla de clasa II

Cupla de clasa III-a (sferica)

Numita si cupla sferica. Partile componente ale unei astfel de cuple sunt: o sfera si o piesa care cuprinde partial sfera (Fig.23).

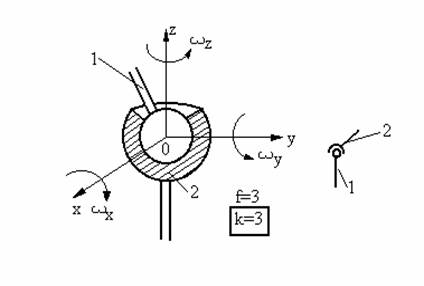
Fig.23 Cupla sferica

Cupla sferica este o cupla de clasa III deoarece introduce trei constringeri, deplasarea de-a lungul celor trei axe de coordonate.V_x=Vy=Vz=0 deci k=3.

Este una dintre cuplele des utilizate la constructia robotilor paraleli. Acest tip de cupla este folosita la legarea platformei superioare sau inferioare de picioarele robotului paralel.

Cupla de clasa IV-a (rototranslatie)

Este formata din arborele 1 si respectiv lagarul 2 de acelasi diametru cu arborele.

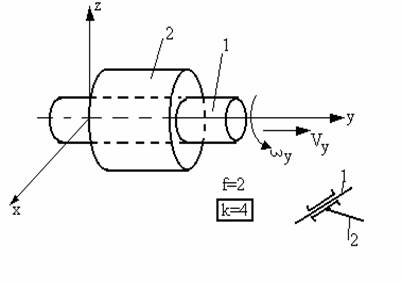
Fig.24 Cupla de rototranslatie

Introduce patru constringeri (k=4) si anume: translatia de-a lungul axelor OX (Vx=0) si OZ (V_z=0) si rotatia in jurul acelorasi axe (w_x w_z

Cupla de clasa V-a (rotatie R)

Este formata din arborele 1 prevazut cu umeri si lagarul 2. Acest tip de cupla introduce cinci constringeri (k=5) si anume translatia pe cele trei axe OX, OY, OZ (Vx=Vy=Vz=0) si rotatiile in jurul axelor OX si OZ (w_x w_z=0). Permite deci doar rotatia in jurul axei OY.

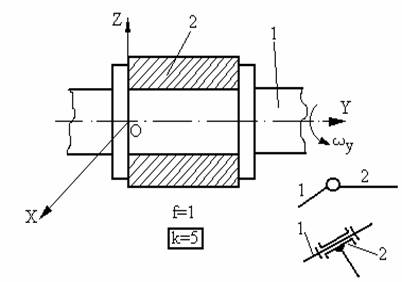
Fig.25 Cupla de rotatie

Cupla de clasa V-a (translatie T)

Este tot o cupla de clasa a V-a (k=5). In acest caz este permisa doar o singura miscare, translatia de-a lungul axei OY, toate celelalte fiind blocate.

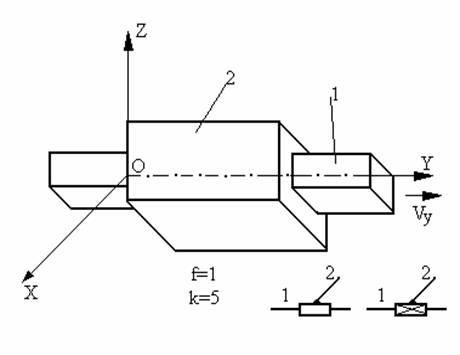
Fig. 26 Cupla de translatie

3 Lanturi cinematice

O reuniune de elemente cinematice legate intre ele cu cuple cinematice reprezinta lanturi cinematice.Lanturile cinematice pot fi deschise (Fig. 28) sau inchise (Fig. 29 a,b), simple cind fiecare element este cel mult binar adica se leaga de cel putin alte doua elemente (Fig.28, Fig. 29 a) sau complexe cind cel putin un element este polinar, adica se leaga de cel putin trei elemente (Fig. 29 b).

Lanturile cinematice mai pot plane cind toate elementele lantului executa miscari in plan sau in plane paralele, sau spatiale cind cel putin un element executa o miscare spatiala.

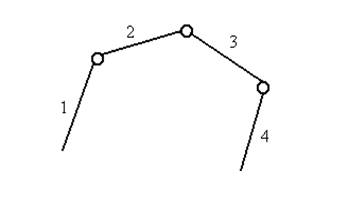
Fig. 28 Lant cinematic deschis

Gradul de libertate L al unui lant cinematic se va obtine prin scaderea din numarul total al celor e elemente cinematice considerate libere in spatiu, adica din 6e, a numarului total K de legaturi:

(5)

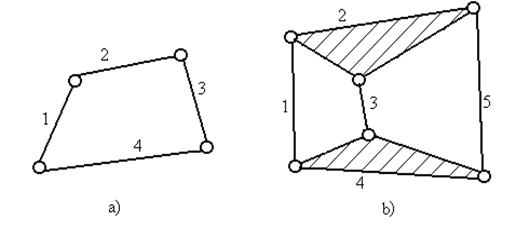
Fig. 29 Lanturi cinematice inchise simple si complexe

Numarul total de legaturi se determina cu relatia:

(6)

unde k reprezinta numarul de constringeri pe care le introduce o cupla de clasa k.

Prin inlocuirea formulei (6) in formula (5) se obtine formula structurala a lanturilor cinematice spatiale generale:

(7)

4 Mecanisme

Mecanismul se defineste ca fiind lantul cinematic inchis care are un element fix si care se bucura de proprietatea ca la o pozitie data a elementului conducator sau a elementelor conducatoare, pentru toate celelalte elemente rezulta pozitii univoc determinate, deci se bucura de proprietatea de desmodromie. Un mecanism are elemente conduse, la care se cunosc legile conducatoare si elemente conduse la care se pot determina legile de miscare din cele ale elementelor conducatoare.

Gradul de mobilitate M al unui mecanism se defineste ca fiind egal cu numarul de miscari independente pe care le poate primi din afara.

Deoarece mecanismele provin din lanturi cinematice la care s-a fixat un element, gradul de mobilitate se va determina scazind din gradul de libertate L al lantului cinematic cele sase miscari blocate de batiu:

(8)

adica

(9)

unde n=e-1 reprezinta numarul de elemente cinematice mobile ale mecanismului.

Formula (9) este cunoscuta si sub denumirea de formula structurala sau formula mobilitatii mecanismelor.