| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Literatūra:
1. Šteiners K. Augstaka matematika III daļa. R.: Zvaigzne ABC, 1997.
2. Bože D., Bieza L., Siliņa B., Strence A. Uzdevumu krajums augstakaja matematika. - R.; Zvaigzne ABC, 2001.
3. Volodko I. Augstaka matematika: īss teorijas izklasts, uzdevumu risinajumu paraugi I daļa., R.: Zvaigzne ABC, 2008.
Bieži ir svarīgi zinat, par cik izmainas funkcijas vērtība, ja kada definīcijas apgabala punkta palielina vai samazina argumenta vērtību. Piemēram, alpīnistam ir svarīgi zinat atmosfēras spiediena izmaiņu, uzkapjot no vienas nometnes līdz nakamajai.
Aplūkosim divas noteikta secība izraudzītas
argumenta vērtības ![]() un
un ![]() no funkcijas
no funkcijas ![]() definīcijas
apgabala. Funkcijas vērtības šajos punktos ir attiecīgi
definīcijas
apgabala. Funkcijas vērtības šajos punktos ir attiecīgi ![]() un
un ![]() .
.
Definīcija. Starpību starp divam argumenta vērtībam ![]() un
un ![]() sauc par argumenta pieaugumu. To apzīmē ar simbolu
sauc par argumenta pieaugumu. To apzīmē ar simbolu ![]() un raksta
un raksta ![]() .
.
Starpību starp divam funkcijas vērtībam ![]() un
un ![]() sauc par funkcijas pieaugumu. To
apzīmē ar simbolu
sauc par funkcijas pieaugumu. To
apzīmē ar simbolu ![]() jeb
jeb ![]() un raksta
un raksta ![]() .
.
Ta ka no ![]() iegūst
iegūst ![]() , tad
, tad
![]() .
.
Argumenta pieaugums ![]() var būt pozitīvs vai negatīvs
atkarība no ta, kura argumenta vērtība ir
lielaka:
var būt pozitīvs vai negatīvs
atkarība no ta, kura argumenta vērtība ir
lielaka: ![]() vai
vai ![]() . Ja argumenta pieaugums
. Ja argumenta pieaugums ![]() ir pozitīvs, tad
funkcijas pieaugums ir pozitīvs lielums vai negatīvs lielums
atkarība no ta, vai funkcija ir augoša vai dilstoša.
ir pozitīvs, tad
funkcijas pieaugums ir pozitīvs lielums vai negatīvs lielums
atkarība no ta, vai funkcija ir augoša vai dilstoša.
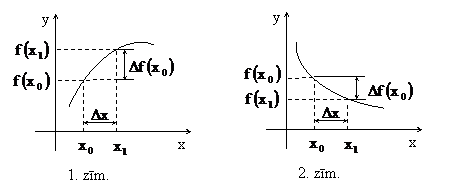
Argumenta un funkcijas pieauguma jēdzieni ilustrēti 1. zīm.
augošai funkcijai un 2. zīm. dilstošai funkcijai.
Ja ir jaatrod funkcijas pieauguma izteiksme
brīvi izraudzīta definīcijas apgabala punkta ![]() , tad
, tad ![]() vieta ievieto
vieta ievieto ![]() un iegūst
funkcijas pieauguma formulu
un iegūst
funkcijas pieauguma formulu
![]() .
.
Piemēri.
Uzrakstīt funkcijas ![]() pieauguma izteiksmi.
pieauguma izteiksmi.
Vispirms atrod ![]() .
.
Tad uzraksta funkcijas pieaugumu ![]() .
.
Uzrakstīt funkcijas ![]() pieauguma izteiksmi un
aprēķinat
pieauguma izteiksmi un
aprēķinat ![]() , ja 1)
, ja 1) ![]() un
un ![]() ; 2)
; 2) ![]() un
un ![]() ; 3)
; 3) ![]() un
un ![]() ; 4)
; 4) ![]() un
un ![]() .
.
Atrod ![]() .
.
Funkcijas pieaugums ir
![]() .
.
No iegūtas izteiksmes var
aprēķinat funkcija ![]() pieaugumu jebkura
definīcijas apgabala punkta. Tatad
pieaugumu jebkura
definīcijas apgabala punkta. Tatad
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
. Uzrakstīt funkcijas ![]() pieauguma izteiksmi.
pieauguma izteiksmi.
Vispirms atrod ![]() .
.
Funkcijas pieauguma izteiksme ir:
![]() .
.
Uzrakstīt funkcijas ![]() pieauguma izteiksmi.
pieauguma izteiksmi.
Rīkojoties līdzīgi ka iepriekšējos piemēros, iegūstam
![]() ,
,
Vingrinajumi
2. Funkcijas nepartrauktība
Daudzi procesi noris nepartraukti. Piemēram, ūdens spiediens uz akvalangistu pieaug nepartraukti, palielinoties ieniršanas dziļumam. Tas nozīmē, ka, mazliet palielinot dziļumu, nedaudz pieaug arī spiediens. Nepartrauktiem procesiem raksturīgi, ka mazam argumenta izmaiņam atbilst mazas funkcijas izmaiņas.
Definīcija.
Funkcija f ir nepartraukta punkta ![]() , ja šis punkts pieder pie funkcijas definīcijas
apgabala un bezgalīgi mazam argumenta pieaugumam
, ja šis punkts pieder pie funkcijas definīcijas
apgabala un bezgalīgi mazam argumenta pieaugumam ![]() atbilst arī
bezgalīgi mazs funkcijas pieaugums
atbilst arī
bezgalīgi mazs funkcijas pieaugums ![]() , t. i.
, t. i. ![]() .
.
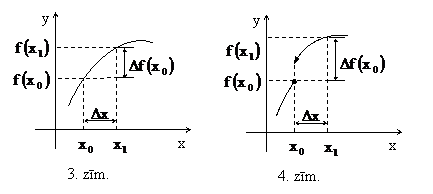
3.
zīmējuma paradīts punkta ![]() nepartrauktas
funkcijas grafiks. Neierobežoti samazinot argumenta pieaugumu
nepartrauktas
funkcijas grafiks. Neierobežoti samazinot argumenta pieaugumu ![]() , arī funkcijas pieaugums
, arī funkcijas pieaugums ![]() samazinas
neierobežoti.
samazinas
neierobežoti.
Savukart 4.
zīmējuma dota partraukta funkcija ir definēta
punkta ![]() , taču, argumenta pieaugumam
, taču, argumenta pieaugumam ![]() tiecoties uz nulli,
funkcijas pieaugums šaja punkta netiecas uz nulli.
tiecoties uz nulli,
funkcijas pieaugums šaja punkta netiecas uz nulli.

Turpretim 5. un 6. zīmējuma paradītas
partrauktas funkcijas punkta ![]() nav definētas.
nav definētas.
Izšķir divu veidu
partraukuma punktus. Ievērosim, ka 4. un 5.
zīmējuma attēloto funkciju vienpusējas
robežas, kad ![]() nav bezgalība.
Šados gadījumos saka, ka
nav bezgalība.
Šados gadījumos saka, ka ![]() funkcijai pirma veida partraukuma punkts.
Savukart 6. zīmējuma funkcijai
funkcijai pirma veida partraukuma punkts.
Savukart 6. zīmējuma funkcijai ![]() . Punktu
. Punktu ![]() sauc par funkcijas otra veida partraukuma
punktu.
sauc par funkcijas otra veida partraukuma
punktu.
No nepartrauktības definīcijas var iegūt šadu secinajumu: ja
![]() ,
,
tad
![]() jeb
jeb
![]() . (1)
. (1)
Ta ka ![]() ir konstants lielums
attiecība pret
ir konstants lielums
attiecība pret ![]() , tad
, tad
![]() . (2)
. (2)
Ta ka ![]() un
un ![]() , ja
, ja ![]() tad no vienadībam
(1) un (2) iegūstam, ka
tad no vienadībam
(1) un (2) iegūstam, ka
![]() .
.
Tatad: ja funkcija ir nepartraukta
punkta ![]() , tad funkcijas robeža, kad
, tad funkcijas robeža, kad ![]() , ir vienada ar funkcijas vērtību punkta
, ir vienada ar funkcijas vērtību punkta ![]() .
.
Var pieradīt, ka no vienadības
![]() seko
vienadība
seko
vienadība ![]() . Tatad abi apgalvojumi ir savstarpēji ekvivalenti:
. Tatad abi apgalvojumi ir savstarpēji ekvivalenti:
![]()
![]() .
.
TEORĒMAS PAR NEPARTRAUKTAM FUNKCIJAM
Ja funkcijas f(x) un g(x) ir
nepartrauktas punkta a, tad šaja punkta ir arī
nepartrauktas funkcijas ![]() ,
, ![]() un
un ![]() (ja
(ja ![]() ).
).
Ja funkcija g(x) ir
nepartraukta punkta a un funkcija f(y) ir nepartraukta
punkta ![]() , tad salikta funkcija
, tad salikta funkcija ![]() ir nepartraukta
punkta a.
ir nepartraukta
punkta a.
Katra elementara funkcija ir nepartraukta sava definīcijas apgabala.
(Veierštrasa teorēma) Ja funkcija ir nepartraukta slēgta intervala, tad šaja intervala ta ir ierobežota un vismaz viena intervala punkta sasniedz savu minimalo vērtību m un vismaz viena intervala punkta sasniedz savu maksimalo vērtību M.
Piemēri.
Pieradīt, ka
funkcija ![]() ir nepartraukta
visiem realiem x.
ir nepartraukta
visiem realiem x.
Atradīsim dotas funkcijas pieauguma izteiksmi:
Aprēķinasim ![]() :
:
![]() .
.
Ta ka ![]() visiem realiem x,
tad funkcija
visiem realiem x,
tad funkcija ![]() ir nepartraukta
visiem realiem x.
ir nepartraukta
visiem realiem x.
Pieradīt, ka funkcija ![]() ir nepartraukta
visiem realiem x.
ir nepartraukta
visiem realiem x.
![]()
![]()
Ta ka ![]() visiem realiem x,
tad funkcija
visiem realiem x,
tad funkcija ![]() ir nepartraukta
visiem realiem x.
ir nepartraukta
visiem realiem x.
. Noteikt funkcijas ![]() partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
Dota funkcija nav definēta punkta ![]() , tatad tas ir partraukuma punkts. Lai noteiktu
ta veidu, aprēķinasim vienpusējas robežas:
, tatad tas ir partraukuma punkts. Lai noteiktu
ta veidu, aprēķinasim vienpusējas robežas:
![]() ,
,
![]() .
.
Ta ka abas vienpusējas
robežas ir bezgalības, punkts ![]() ir otra veida partraukuma
punkts.
ir otra veida partraukuma
punkts.
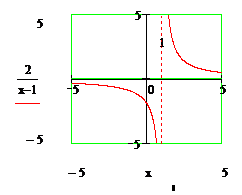
Noteikt funkcijas ![]() partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
Šī funkcija nav definēta, ja ![]() . Tas ir šīs funkcijas partraukuma punkts.
. Tas ir šīs funkcijas partraukuma punkts.
Atradīsim vienpusējas robežas:
![]() ,
,
![]() .
.
Ta ka robeža no kreisas puses
ir bezgalība, tad ![]() ir otra veida partraukuma
punkts.
ir otra veida partraukuma
punkts.
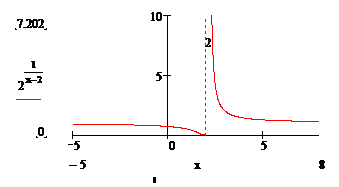
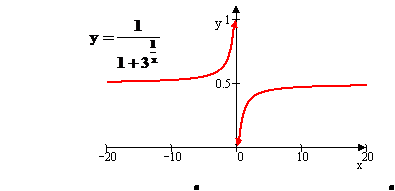
Noteikt funkcijas  partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
partraukuma
punktu un ta veidu. Uzzīmēt funkcijas grafiku partraukuma
punkta apkartnē.
Funkcija nav definēta, ja ![]() , tas ir šīs funkcijas partraukuma punkts.
, tas ir šīs funkcijas partraukuma punkts.
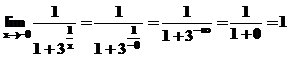 ,
,
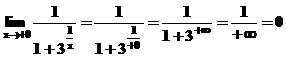 .
.
Abas vienpusējas robežas ir
galīgas. Tatad ![]() ir pirma veida
partraukuma punkts.
ir pirma veida
partraukuma punkts.
Uzdevumi: 726., 727., 728.‑739. uzd. no uzd. kraj augst. mat.
753. uzd.
Izmantojot
nepartrauktu funkciju īpašības, pieradīt, ka
vienadojumam ![]() intervala
intervala ![]() ir vismaz viena
reala sakne.
ir vismaz viena
reala sakne.
Aprēķinasim funkcijas ![]() vērtības
dota intervala galapunktos:
vērtības
dota intervala galapunktos:
![]() ;
; ![]() .
.
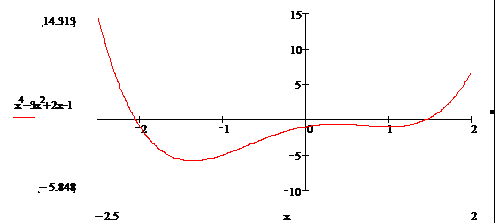 Ta ka funkcija
Ta ka funkcija ![]() ir nepartraukta,
tad intervala
ir nepartraukta,
tad intervala ![]() ta pieņem
visas vērtības no
ta pieņem
visas vērtības no ![]() līdz 7,
tatad arī 0. Tapēc var apgalvot, ka dotaja
intervala eksistē vismaz viena tada x vērtība,
kurai
līdz 7,
tatad arī 0. Tapēc var apgalvot, ka dotaja
intervala eksistē vismaz viena tada x vērtība,
kurai ![]() .
.
3. Ievads atvasinajuma jēdziena izpratnei.
Aplūkosim ķermeņa kustību taisna virziena ar mainīgu atrumu. Lietosim apzīmējumus:
t laiks,
s attalums,
v atrums.
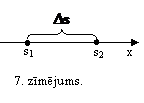 Tad ķermeņa veiktais attalums ir laika funkcija
Tad ķermeņa veiktais attalums ir laika funkcija ![]() .
.
Pieņemsim, ka ķermenis desmitas
sekundes beigas atrodas punkta ar koordinatu ![]() , bet pēc 10 sekundēm ta koordinata ir
, bet pēc 10 sekundēm ta koordinata ir ![]() . (Skat. 7.zīm.) Tad laika intervala
. (Skat. 7.zīm.) Tad laika intervala ![]() tas ir veicis
attalumu
tas ir veicis
attalumu ![]() un
un ![]() . Aprēķinasim ķermeņa vidējo
atrumu šaja laika intervala
. Aprēķinasim ķermeņa vidējo
atrumu šaja laika intervala ![]() .
.
Ja laika intervalu samazinasim, tad
samazinasies arī veiktais attalums ![]() un mainīsies
vidējais atrums. (Skat. tabulu.)
un mainīsies
vidējais atrums. (Skat. tabulu.)
|
Laika intervals |
|
|
|
|
|
|
| |||||
|
| |||||
|
|
No tabulas datiem redzams, ka maziem laika intervaliem atruma vidēja vērtība maz atšķiras no 10 m/s. Ir pamats secinat, ka desmitas sekundes beigas ķermeņa atrums ir 10 m/s. Fizika to sauc par momentano atrumu.
Precīzi momentana atruma
vērtību iegūtu, ja laika sprīdi ![]() ņemtu
bezgalīgi mazu t. i., kad
ņemtu
bezgalīgi mazu t. i., kad ![]() . Tad
. Tad ![]() .
.
Ja attaluma funkcijas vieta ņemam
funkciju ![]() , tad
, tad ![]() ir argumenta pieaugums
kada intervala, bet
ir argumenta pieaugums
kada intervala, bet ![]() funkcijas pieaugums
šaja intervala. Attiecība
funkcijas pieaugums
šaja intervala. Attiecība ![]() parada funkcijas
izmaiņas vidējo atrumu. Robežgadījuma, kad
parada funkcijas
izmaiņas vidējo atrumu. Robežgadījuma, kad ![]() , šī attiecība parada funkcijas
izmaiņas atrumu punkta. Matematika to sauc par
funkcijas atvasinajumu.
, šī attiecība parada funkcijas
izmaiņas atrumu punkta. Matematika to sauc par
funkcijas atvasinajumu.
4. Atvasinajuma definīcija.
Apskatīsim funkciju ![]() . Izvēlēsimies kadu argumenta vērtību
. Izvēlēsimies kadu argumenta vērtību
![]() un dosim tam pieaugumu
un dosim tam pieaugumu
![]() . Atradīsim funkcijas pieaugumu
. Atradīsim funkcijas pieaugumu ![]() .
.
Definīcija.
Par
funkcijas atvasinajumu punkta ![]() funkcijas pieauguma un
argumenta pieauguma attiecības robežu šaja punkta, kad
argumenta pieaugums tiecas uz nulli.
funkcijas pieauguma un
argumenta pieauguma attiecības robežu šaja punkta, kad
argumenta pieaugums tiecas uz nulli.
Atvasinajumu apzīmē ar simbolu ![]() jeb
jeb ![]() .
.
Atvasinajuma punkta definīcijas
formula: ![]() .
.
Parasti funkcijas atvasinajumu meklē jebkurai argumenta vērtībai x, kurai atvasinajums eksistē. Tad atvasinajuma definīcijas formula ir
![]() jeb
jeb ![]()
Jaatceras:
5. Atvasinašanas formulas.
Izmantojot atvasinajuma definīciju, atradīsim dažam pamatfunkcijam atvasinašanas formulas.
1. Konstantas funkcijas atvasinajums.
Ja ![]() , tad arī
, tad arī ![]() un
un ![]() . Tatad
. Tatad ![]() .
.
Tatad konstanta lieluma atvasinajums ir nulle.
Piemēram. ![]() ,
, ![]() .
.
2. Funkcijas ![]() atvasinajums.
atvasinajums.
Atradīsim ![]() .
.
Tad ![]() .
.
3. Funkcijas ![]() atvasinajums.
atvasinajums.
Funkcijas pieaugums ir
![]() .
.
Atvasinajums ![]() .
.
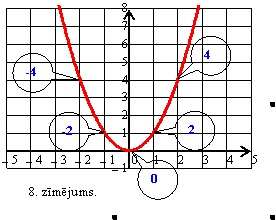 Aprēķinasim šīs funkcijas atvasinajumu
vairakos punktos:
Aprēķinasim šīs funkcijas atvasinajumu
vairakos punktos:
![]() ;
; ![]() ;
; ![]() ;
; 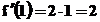 ;
; ![]()
8.
zīmējuma paradīts funkcijas ![]() grafiks.
Aplīšos ierakstītas šīs funkcijas atvasinajuma
vērtības atbilstošajos punktos. Varam secinat, ka augošai
funkcijai atvasinajuma vērtības ir pozitīvas,
dilstošai negatīvas. Ja funkcija aug straujak, tad
atvasinajuma vērtība ir lielaka. Dilšanas
intervala otradi. Parabolas virsotnē atvasinajums ir
0.
grafiks.
Aplīšos ierakstītas šīs funkcijas atvasinajuma
vērtības atbilstošajos punktos. Varam secinat, ka augošai
funkcijai atvasinajuma vērtības ir pozitīvas,
dilstošai negatīvas. Ja funkcija aug straujak, tad
atvasinajuma vērtība ir lielaka. Dilšanas
intervala otradi. Parabolas virsotnē atvasinajums ir
0.
4. Funkcijas ![]() atvasinajums.
atvasinajums.
Šīs funkcijas pieauguma izteiksme ir atrasta iepriekš un ta ir:
![]() .
.
Pēc definīcijas atrodam šīs funkcijas atvasinajumu:
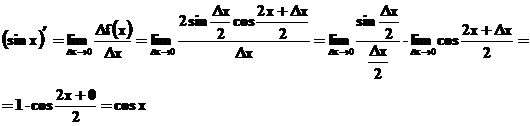
5. Pakapes funkcijas atvasinajums.
Pakapes funkcijas atvasinašanas formulu jebkuram realam kapinatajam šeit nepieradīsim. Šī formula ir
![]()
Aplūkosim dažus piemērus:
![]()
![]()
![]()
![]()
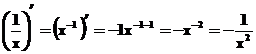 ;
; 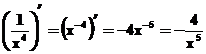 ;
;
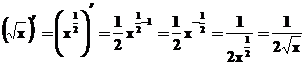 ;
;
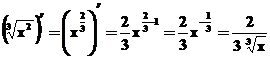 .
.
Der atcerēties dažas ar pakapi saistītas sakarības:
![]()
![]()
![]()
![]()
![]()
Talak dota biežak lietoto funkciju atvasinašanas formulas.
ATVASINAŠANAS FORMULAS
|
PAMATFUNKCIJAS ATVASINAŠANAS FORMULA |
SALIKTAS FUNKCIJAS ATVASINAŠANAS FORMULA |
|
|
|
|
6. Atvasinašanas likumi.
Aplūkosim funkcijas
![]() un
un ![]() , kuram eksistē atvasinajumi
, kuram eksistē atvasinajumi ![]() un
un ![]() .
.
1. Funkciju summas vai starpības atvasinašana:
![]()
Piemēri.
![]() ;
;
![]() .
.
2. Funkciju reizinajuma atvasinajums.
![]()
Piemēri.
![]() ;
;
![]() .
.
3. Konstanta reizinataja iznešana pirms atvasinajuma zīmes:
![]()
Piemēri.
![]() ;
;
![]() ;
;
![]() .
.
4. Funkciju dalījuma atvasinajums.

Piemēri.
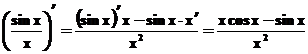 ;
;
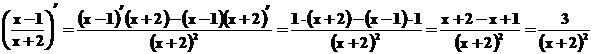 ;
;
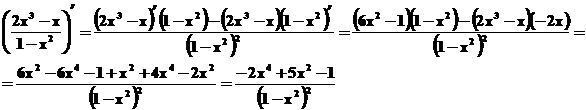
Vingrinajumi.
Izpildīt 1. uzdevuma I, II un III.
1. uzdevums.
ATVASINAT DOTO FUNKCIJU:
|
I |
II |
III |
IV |
|
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
|
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
|
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
|
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
n)
|
7. Salikta funkcija un tas atvasinašana.
Apskatīsim divas funkcijas ![]() , kur
, kur ![]() un, kur
un, kur ![]() . Ta ka pirmas funkcijas definīcijas
apgabalam un otras funkcijas vērtību kopai ir kopīga
daļa, tad var izveidot funkciju
. Ta ka pirmas funkcijas definīcijas
apgabalam un otras funkcijas vērtību kopai ir kopīga
daļa, tad var izveidot funkciju ![]() . Ta ir salikta funkcija. To veido arēja
funkcija
. Ta ir salikta funkcija. To veido arēja
funkcija ![]() un iekšēja
funkcija
un iekšēja
funkcija ![]() .
.
Visparīga
veida saliktu funkciju varam uzrakstīt ![]() , kur arēja funkcija ir
, kur arēja funkcija ir ![]() un
iekšēja funkcija
un
iekšēja funkcija ![]() .
.
Piemēri.
Dotajai saliktai funkcijai noteikt iekšējo un arējo funkciju.
1) ![]()
![]()
![]() un
un ![]()
2) ![]()
![]()
![]() un
un ![]()
3) ![]()
![]()
![]() ,
, ![]() un
un ![]()
4) ![]()
![]()
![]() un
un ![]()
5) ![]()
![]()
![]() un
un ![]()
6) ![]()
![]()
![]() ,
, ![]() un
un ![]()
7) ![]()
![]()
![]() ,
, ![]() ,
, ![]() un
un ![]()
Saliktu funkciju ![]() atvasina pēc
formulas:
atvasina pēc
formulas:
![]() jeb
jeb ![]()
Lai atvasinatu saliktu funkciju, vispirms atvasina arējo funkciju, pēc tam iekšējo funkciju un iegūtos atvasinajumus sareizina.
Piemēri.
Dažus piemērus pildīsim ļoti pakapeniski.
1. Atvasinat funkciju ![]() .
.
Arēja funkcija ir ![]() , bet iekšēja funkcija
, bet iekšēja funkcija ![]() . Vispirms atvasina arējo funkciju
. Vispirms atvasina arējo funkciju ![]() , pēc tam iekšējo funkciju
, pēc tam iekšējo funkciju ![]() .
.
Tad ![]() .
.
2. Atvasinat funkciju ![]() .
.
Arēja funkcija ![]() , iekšēja funkcija
, iekšēja funkcija ![]() .
.
To atvasinajumi ![]() ,
, ![]() .
.
Tad ![]() .
.
3. Atvasinat funkciju ![]() .
.
Arēja funkcija ![]() , iekšēja funkcija
, iekšēja funkcija ![]() .
.
To atvasinajumi ![]() ,
, ![]() .
.
Tad ![]() .
.
4. Atvasinat funkciju ![]() .
.
Tagad pierakstu saīsinasim.
Arējas funkcijas atvasinajums ![]() ,
,
iekšējas funkcijas
atvasinajums ![]() .
.
Tad ![]() .
.
5. Atvasinat funkciju ![]() .
.
Talak jau lietošu īsu pierakstu. Ja nepieciešams, tad pēc iepriekšējiem piemēriem var atvasinat pakapeniski.
![]()
(Lietota formula ![]() .)
.)
6. Atvasinat funkciju ![]() .
.
![]() (Lietotas formulas
(Lietotas formulas ![]() un
un ![]() .)
.)
Vingrinajumi.
1. uzdevums IV un 2. uzdevums.
2. uzdevums.
Atvasinat dotas funkcijas.
1. ![]() ; 2.
; 2.
![]() ; 3.
; 3. ![]() ;
;
4. ![]() ; 5.
; 5. ![]() ; 6.
; 6. ![]() ;
;
7. ![]() ; 8.
; 8.
![]() ; 9.
; 9.
![]() ;
;
10. ![]() ; 11.
; 11.
![]() ; 12.
; 12.
![]() ;
;
13. ![]() ; 14.
; 14. ![]() ; 15.
; 15.
![]() ;
;
16. ![]() ; 17.
; 17.
![]() ; 18.
; 18.
![]() ;
;
19. ![]() ; 20.
; 20.
 ; 21.
; 21.
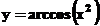
8. Funkcijas atvasinajuma aprēķinašana dotaja punkta.
Pieņemsim, ka dota funkcija ![]() un jaatrod tas atvasinajums
un jaatrod tas atvasinajums ![]() .
.
Lai to izdarītu,
atvasina doto funkciju,
aprēķina ![]() .
.
Piemērs.
Aprēķinat
funkcijas ![]() atvasinajumu
argumenta vērtībai
atvasinajumu
argumenta vērtībai ![]() .
.
Atvasinasim doto funkciju. Ta ir salikta funkcija.
![]()
Aprēķinasim ![]() .
.
Vingrinajumi.
3. uzdevums.
3. uzdevums.
APRĒĶINAT DOTAS FUNKCIJAS ATVASINAJUMU NORADĪTAJA PUNKTA
a) ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
b) ![]()
![]() ;
; ![]() ;
; ![]() ;
;
c) ![]()
![]() ;
; ![]() ;
; ![]() ;
;
d) ![]()
![]() ;
; ![]() ;
; ![]() ;
;
e) ![]()
![]() ;
; ![]() ;
; ![]() .
.
9. Apslēptas funkcijas atvasinašana.
Funkcija ![]() ir dota
atklata veida. Savukart ar vienadību
ir dota
atklata veida. Savukart ar vienadību ![]() funkcija y ir dota
apslēpta veida.
funkcija y ir dota
apslēpta veida.
Lai atrastu apslēptas funkcijas ![]() atvasinajumu
atvasinajumu ![]() , vienadības
, vienadības ![]() abas puses atvasina
pēc x un no iegūtas sakarības izsaka
abas puses atvasina
pēc x un no iegūtas sakarības izsaka ![]() .
.
Piemēri.
1. Noteikt ![]() funkcijai
funkcijai ![]() .
.
Atvasinasim doto vienadību pēc x, ņemot vēra, ka y2 ir salikta funkcija:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
2. Noteikt ![]() funkcijai
funkcijai ![]() .
.
Atvasinasim doto vienadību pēc x:
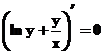
![]()
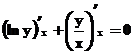
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
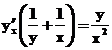
![]()
![]()
![]()
![]()
![]() .
.
10. Logaritmiska atvasinašana.
Vispirms jaatkarto dažas logaritmu
īpašības: ![]() .
.
Mums ir jaatvasina funkcija ![]() . Šī funkcija neatbilst pakapes vai
eksponentfunkcijas definīcijai. Līdz ar to nevaram lietot
atbilstošas formulas. Tapēc logaritmēsim šo
funkciju.
. Šī funkcija neatbilst pakapes vai
eksponentfunkcijas definīcijai. Līdz ar to nevaram lietot
atbilstošas formulas. Tapēc logaritmēsim šo
funkciju.
Tad ![]() . Pielietojot logaritmu īpašību
. Pielietojot logaritmu īpašību ![]() . Vienadības abas puses atvasinasim pēc
x:
. Vienadības abas puses atvasinasim pēc
x: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Apskatīsim vēl dažus piemērus.
1. Atvasinat funkciju ![]() , to vispirms logaritmējot.
, to vispirms logaritmējot.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Atvasinat funkciju ![]() , to vispirms logaritmējot.
, to vispirms logaritmējot.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
11. Parametriski dotas funkcijas atvasinašana.
Ja funkcija ![]() ir uzdota
parametriska veida, t. i., ar sistēmu
ir uzdota
parametriska veida, t. i., ar sistēmu
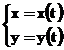 ,
,
tad funkcijas ![]() atvasinajumu
atrod ar sakarību
atvasinajumu
atrod ar sakarību ![]() .
.
Piemērs.
Atvasinat parametriska veida dotu
funkciju 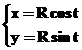 . (Grafiks ir riņķa līnija ar centru
koordinatu sakumpunkta.)
. (Grafiks ir riņķa līnija ar centru
koordinatu sakumpunkta.)
Vispirms atrod ![]() un
un ![]() . Tad
. Tad ![]() .
.
12. Augstaku kartu atvasinajumi.
Pieņemsim, ka funkcijai ![]() eksistē
atvasinajums
eksistē
atvasinajums ![]() . Ta ka šis atvasinajums arī ir
funkcija, tad to var atvasinat. Līdz ar to iegūstam dotas
funkcijas otras kartas
atvasinajumu
. Ta ka šis atvasinajums arī ir
funkcija, tad to var atvasinat. Līdz ar to iegūstam dotas
funkcijas otras kartas
atvasinajumu ![]() .
.
Otras kartas atvasinajumu
vēlreiz atvasinot, iegūst trešas
kartas atvasinajumu ![]() .
.
Talak seko ceturtas kartas
atvasinajums, kuru apzīmē ![]() u. t. t.
u. t. t.
Tie ir dotas funkcijas augstaku kartu atvasinajumi.
Piemēri.
1. Atrast otras, trešas un
ceturtas kartas atvasinajumu funkcijai ![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Atrast otras kartas atvasinajumu
funkcijai ![]() .
.
![]() ,
,
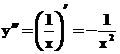 .
.
Vingrinajumi.
923. uzdevums no uzdevumu krajuma augstakaja matematika.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3152
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved
Distribuie URL
Adauga cod HTML in site