Modele spatiale ale alegerilor

Modele spatiale ale alegerilor

Ideea lui Black, de a admite numai profile in care preferintele individuale au un singur varf, are - asa cum am vazut - o interpretare spatiala evidenta. D. Black (1958), A. Downs (1957) si, urmandu-i pe acestia, multi alti autori au construit modele spatiale ale alegerilor. Acesti autori au argumentat ca: 1) alternativa aleasa va fi situata in "centrul" distributiei preferintelor individuale; iar 2) stabilitatea politica (in acest caz, alegerea unei anumite alternative) depinde atat de preferintele individuale, cat si de regulile utilizate pentru agregarea acestora. Modelele spatiale sunt intuitive: putem oferi reprezentari usor de inteles ale unor situatii altminteri mai complexe; de aceea, apelul la aceste modele se poate dovedi fructuos, caci putem sesiza consecinte nebanuite ale ipotezelor noastre, conexiuni mai greu de observat, putem face noi ipoteze.

Modelele spatiale ale diverselor aspecte ale politicii nu sunt insa o inventie noua. Dimpotriva, cercetatorii fenomenului politic au teoretizat de multa vreme astfel de chestiuni, iar practica politica a dezvoltat mecanisme care pot fi cel mai usor intelese daca facem apel la astfel de modele. Probabil ca primul ganditor care a oferit un model spatial al politicii a fost Aristotel (384 - 322 i.H.), in lucrarea sa Politica (2001).

Dupa Aristotel, pentru fiecare individ in parte viata fericita este cea masurata, cea in care sunt evitate excesele. La fel, considera el, trebuie sa stea lucrurile si in cazul cetatii. Cum se poate argumenta insa in acest sens? Aristotel pleaca de la supozitia ca membrii unei cetati pot fi impartiti potrivit criteriului averii:

in fiecare cetate exista trei parti: unii sunt cei foarte bogati, altii sunt cei foarte saraci, iar in al treilea rand sunt cei de conditie medie. Deoarece am cazut de acord asupra faptului ca masura si medietatea sunt cele mai bune, este evident ca si dintre toate agoniselile cea mai buna este o avere medie. (IV, 11, 1295b)

Membrii celor trei grupuri, argumentaza Aristotel, se comporta diferit: cei din primul grup au un exces de prosperitate, de forta, de prieteni si alte asemenea si de aceea nu doresc si nici nu se pricep sa se supuna - dimpotriva, sunt tentati sa conduca despotic. Cei saraci nu se pricep sa conduca; mai mult, ei sunt invidiosi si doresc bunurile celor care au mai mult decat ei. Membrii celor de conditie medie au cu totul alte caracteristici: ei, sustine Aristotel, nu au dorinta de a avea puterea si nici nu doresc bunurile semenilor lor (dupa cum nici altii nu le doresc bunurile lor). Asadar, pozitia pe scala bogatiei reprezinta, dupa Aristotel, un indicator al modului in care se constituie preferintelele membrilor cetatii.

Unde trebuie situata puterea? Aristotel indica un numar de indicatori in functie de care se poate da un raspuns. Mai intai, argumenteaza el, puterea politica trebuie sa promoveze virtutea cetatii: ea trebuie sa faca astfel incat la viata cetatii sa fie capabili sa participe toti. Dar, in al doilea rand, puterea politica trebuie sa produca siguranta. Acolo unde "clasa de mijloc este numeroasa nu exista nici o disensiune si nici o revolta in cadrul constitutiilor", asa cum se intampla insa fie cand regimul este oligaric, fie cand saracii covarsesc prin numar (1296a). Un al treilea indicator este stabilitatea:

[U]nde sunt preponderenti cei de conditie medie, fie in raport cu ambele extreme, fie cu una singura, acolo este posibila o constitutie stabila. Caci nu exista nici un pericol ca bogatii sa se alieze cu saracii impotriva acestora vreodata, pentru ca niciodata cei din urma nu vor dori sa fie sclavii celor dintai. Iar daca ei ar dori sa caute o forma mai comuna de <viata>, nu vor gasi alta decat aceasta, pentru ca o guvernare alternativa nu ar rezista din cauza neincrederii lor reciproce Cu cat o constitutie este mai bine combinata, cu atat este mai stabila (Politica, IV, XII, 1296b - 1297a)

De aici concluzia lui Aristotel: intr-o guvernare buna, trebuie sa conduca cei de conditie medie: "Este insa intotdeauna necesar ca legislatorul sa se sprijine pe cei de conditie medie" (1296b). Motivul este ca daca cei de conditie medie sunt mai numerosi, ei sunt mai puternici decat cele doua <extreme>, ori de nu, <cel putin> decat una dintre ele" (1295b). Cu alte cuvinte, structura unei societati in care exista o guvernare buna trebuie sa fie aceea in care cei de conditie medie sunt cei mai numerosi: distributia membrilor cetatii dupa avere este cea indicata de Figura 1, nu si de Figura 2.

Vom vedea mai jos ca ideea lui Aristotel ca puterea se situeaza in dreptul celor aflati la mijloc este la baza modelelor spatiale ale alegerilor si poate fi reconstruita intr-un mod riguros. Pentru a intelege aceste modele spatiale, sa incepem cu un exemplu.

Sa presupunem ca un Consiliu al unei facultati din Universitatea X trebuie sa decida daca in anul universitar urmator taxele platite de catre studenti vor fi sau nu modificate. Sa presupunem ca din Consiliu fac parte sapte persoane: A, B, C, D, E, F si G (dintre acestia, C si D sunt studenti, iar A este decanul facultatii). Ei se raporteaza la nivelul actual al taxelor si propun o modificare a acestora. Sa notam cu litera a alternativa propusa de persoana A, cu b alternativa propusa de persoana B etc. Propunerile lor sunt redate in tabelul de mai jos:

Intrebarea este: putem oare folosi intuitiile care vin din faptul ca putem reprezenta spatial propuerile avansate de membrii Consiliului pentru a face o predictie in legatura cu preferintele membrilor lui si, in consecinta, cu felul in care va alege Consiliul o alternativa? Pentru a raspunde la aceasta intrebare, trebuie sa putem determina care sunt preferintele membrilor lui, in raport cu toate cele sapte alternative (care astfel alcatuiesc agenda grupului). Sa pornim de la un fapt evident: fiecare persoana din Consiliu va prefera cel mai mult propunerea pe care o face ea. Vom spune ca pentru fiecare membru al Consiliului, alternativa pe care o propune este punctul sau ideal. Decanul, care trebuie sa gestioneze fondurile facultatii si doreste sa aiba cat mai multi bni la dispozitie, e cel care propune cea mai mare marire a taxelor. In schimb, cei doi studenti (la randul lor alesi de catre colegi in Consiliul Facultatii) incearca nu numai sa se opuna cresterii taxelor, ci chiar o reducere a acestora. Iar unul din membrii Consiliului prefera status quo-ul: nemodificarea taxelor de studii. Daca ne uitam mai cu atentie la punctele ideale ale membrilor Consiliului, observam ca trei din membrii lui doresc o crestere mai mare decat cea propusa de E, si tot atat de multi doresc o crestere mai mica decat cea propusa de E (o persoana vrea pastrarea vechii taxe, iar doua vor chiar reducerea ei); in consecinta, votantul "mediu" este E, al carui punct ideal este o crestere a nivelului taxelor cu 10%.

Daca fiecare din cele sapte persoane este rationala, atunci ea trebuie insa sa poata compara intre ele toate cele sapte alternative si sa isi formeze o preferinta completa si tranzitiva. Sa facem in continuare cateva presupuneri cu privire la felul in care procedeaza fiecare persoana.

• Unidimensionalitatea. Preferintele individuale se formeaza in raport cu o singura chestiune, anume nivelul taxelor de studii. De exemplu, nu e in discutie chestiuea daca unii studenti vor fi sprijiniti financiar de universitate, sau cea a modificarii sistemului de acordare a burselor etc.
• Ordonarea. Fiecare membru al Consiliului prefera cel mai mult punctul sau ideal. Cu alte cuvinte, pe axa determinata de dimensiunea discutata, pentru fiecare persoana exista preferinta ideala, fata de care se vor ordona toate celalalte alternative.
• Preferintele au un singur varf. Aceasta inseamna ca, cu cat o alternativa se indeparteaza mai mult de punctul ideal al unei persoane, cu atat o va prefera mai putin.
• Votul este sincer. O persoana voteaza in favoarea unei alternative in raport cu o alta tinand seama doar de modul in care a comparat cele doua alternative, si nu de rezultatele posibile ale votului in ceea ce priveste alte alternative.

Cateva comentarii sunt necesare in acest loc. Mai intai, asa cum se poate imediat observa, supozitia ca votul este sincer este o reformulare a cerintei lui Arrow de independenta de alternativele irelevante. In al doilea rand, conditia lui Black ca preferintele individuale sa aiba un singur varf decurge din reprezentarea spatiala a punctelor ideale (a se vedea Figura 3; pentru fiecare votant exista o singura alternativa pentru care preferinta este cea mai inalta). Anume, putem reprezenta alternativele ca puncte pe o linie care reprezinta preferintele individuale si fiecare dintre linii are un punct maxim, iar celelalte alternative se situeaua mai jos, pe o parte sau pe alta (sau pe amandoua) ale liniei.

De exemplu, sa ne gandim la persoana G din Consiliu. Ea prefera cel mai mult status quo-ul. Dar daca ar fi sa accpte o crestere a taxelor, atunci i-ar fi mai usor sa admita o crestere a acestora cu 10% (asa cum propune E) decat de 15% (asa cm propune F), fiindca propunerea de crestere a taxelor cu 10% e mai apropiata de punctul sau ideal decat propunerea de crestere cu 15%. Tot asa, daca ar fi sa aleaga intre o dimunuare cu 20% a taxelor (asa cum propune C) si o diminuare a lor cu 25% (asa cum propune D), va prefera prima propunere, care e mai apropiata de punctul sau ideal.

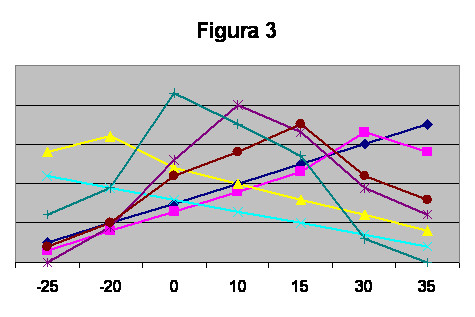
Dar sa presupunem ca G ar urma sa aleaga intre o reducere cu 20% a taxelor si o crestere cu 20% a acestora. Cum va proceda el in acest caz? Supozitiile facute pana acum nu ne permit sa dam un raspuns. Fiindca este posibil ca el sa prefere in general o crestere a taxelor unei reduceri a acestora, si pentru el cresterea cu 15% a lor (cum propune F) sa fie la fel de mult preferata ca si o reducere cu 20% a acestora (cum propune C); sau ar putea sa prefere invers. Vom face - simplificand, pentru ca discutia ulterioara sa fie mai usor de urmarit - presupunerea ca preferintele membrilor Consiliului sunt simetrice:

• Simetria. Propunerile care sunt egal departate de punctul ideal al unei persoane sunt egal preferate, chiar daca departarea este in directii opuse. (Atentie: aceasta proprietate a preferintelor nu trebuie confundata cu proprietatea de simetrie a relatiei de preferinta definita in paragraful 5.2!)

Mai in general, daca j este un membru al grupului, iar x_j este punctul lui ideal, putem sa definim relatia de preferinta intre oricare doua alternative y si z de pe agenda grupului. Avem:

P_j(z,y) = df. |z - x_j| < |z - x_j|

I_j(z,y) = df. |z - x_j| = |z - x_j|

O persoana prefera strict pe y lui z daca distanta dintre y si punctul ei ideal este mai mica decat distanta dintre z si punctul ei ideal; cand cele doua distante sunt egale, persoana e indiferenta intre cele doua alternative. E interesant de notat aici, mai intai, ca definitiile date permit sa deosebim intre alternative in termeni de intensitate a preferintei: cu cat distanta dintre punctul ideal si o alternativa creste, cu atat preferinta e mai slaba. In al doilea rand, definitiile de mai sus merg daca nu preseupunem simetria numai daca alternativele se situeaza de aceeasi parte a punctului ideal; cu simetria, putem compara alternative situate pe laturi diferite ale punctului ideal.

Cu aceste supozitii, putem determina cu usurinta preferintele fiecaruia dintre membrii Consiliului:

A: a > b > f > e > g > c > d

B: b > a > f > e > g > c >d

C: c > d > g > e > f > b > a

D: d > c > g > e > f > b > a

E: e > f > g > b > a > c > d

F: f > e > (g, b) > a > c > d

G: g > e > f > c > d > b > a

Sa comparam acum pereche cu pereche cele sapte alternative. Exista un invingator Condorcet - iar acesta este alternativa e. Sa ne uitam cu atentie la aceasta alternativa. Ea este sustinuta de persoana E. Dintre celelalte sase persoane din Consiliu, trei au un punct ideal mai mari decat E, deci situate la dreapta pe o scala crescatoare: ele sustin cresteri mai mari ale taxelor de scolarizare. De asemenea, tot trei dintre persoanele din Consiliu sustin taxe mai mici, deci pe o scala crescatoare au punctele ideale situate la stanga lui E. (Lucrul acesta este evident daca ne uitam la Figura 3: in ea cele sapte puncte ideale sunt prezentate pe o singura dimensiune - axa orizontala - si sunt aranjate de la stanga la dreapta.) Pozitia sustinuta de E are deci si o alta proprietate: ea este "la mijloc", este pozitia care exprima, cu zicea Aristotel, "medietatea".

E acum momentul sa facem mai precisa aceasta constatare: aceea ca exista o corelatie intre pozitia mediana si cea care este invingator Condorcet.

Primul lucru este sa fomulam definitia pozitiei sau alternativei mediane. Mai intai, fiecarei alternative x aflate pe agenda putem sa ii atasam multimea N_S(x) a persoanelor individuale pentru care alternative x se situeaza la stanga punctului lor ideal. In al doilea rand, fiecarei alternative de pe agenda putem sa ii atasam multimea N_D(x) a persoanelor individuale pentru care alternativa x se situeaza la stanga punctului lor ideal. Acum putem defini alternativa sau pozitia mediana: x_med este pozitia mediana daca si numai daca

N_S(x_med) ≥ |G|/2

N_D(x_med) ≥ |G|/2

Cu alte cuvinte, cel putin jumatate din membrii grupului au punctual ideal la stanga lui x_med si cel putin jumatate din membrii grupului au punctual ideal la dreapta alternativei x_med.

E important sa accentuam ca aici am definit pozitia sau alternativa mediana - dar nu votantul median. Intr-adevar, este posibil in unele cazuri sa definim aceasta pozitie, dar care este ocupata fie de mai multi votanti. Sa luam cateva exemple pentru a face mai clara aceasta sustinere.

Mai intai, sa presupunem in exemplul nostrum ca votantul nostru E are o problema de familie si nu poate veni la vot in ziua cand in Consiliul Facultatii se discuta marimea taxelor de scolarizare. Acum grupul care voteaza are doar sase membri. Sase este un numar par - si stim ca in cazul regulii majoritatii acum sunt posibile balotaje. Observam ca orice pozitie situata intre o crestere nula si una de 15% a taxelor este una mediana. Asadar in acest caz pozitia mediana nu este unica: exista un interval inchis de pozitii mediane. (Se poate verifica faptul ca si pozitiile sustinute de persoanele F si G sunt mediane.)

Uneori mai multe persoane au acelasi punct ideal. Sa presupunem in exemplul nostru ca cei sapte membri ai Consiliului isi modifica optiunile in felul urmator:

Avem iarasi un numar impar de votanti, deci nu apare nici o problema cu existenta pozitiei mediane. Aceasta este 10: caci un numar de cinci membri (asadar > 7/2) ai Consiliului au punctul ideal mai mare sau egal cu 10 (deci la dreapta lui) si un numar de patru (asadar > 7/2) au punctul ideal mai mic sau egal cu 10 (deci la stanga lui). Dar nu exista un unic votant median, ci doi: E si G.

Sa presupunem acum ca A nu poate participa la vot. Atunci grupul are un numar par - sase - de membri. Dar exista in continuare o pozitie mediana, anume iarasi 10, si doi votanti care sustin aceasta pozitie.

Teorema votantului median. Am ajuns acum la unul dintre cele mai importante rezultate obtinute prin apelul la modelele spatiale ale alegerilor.

Teorema votantului median (Black). Sa presupunem ca exista o singura dimensiune si ca preferintele individuale au un singur varf. Atunci, daca x_med este pozitia mediana, atunci numarul voturilor pentru x_med este mai mare sau egal decat numarul voturilor pentru orice alta alternativa.

Demonstratie. Sa observam, mai intai, ca teorema nu cere ca preferintele individuale sa fie simetrice. De aceea, ne raportam la alternativele care se gasesc pe aceeasi parte a pantei care descrie preferinta unui votant. Sa presupunem mai intai ca x < x_med. Toate punctele ideale aflate la dreapta lui x_med sunt mai apropiate de x_med decat de x. Atunci proprietatea ca preferintele au un singur varf garanteaza ca toti votantii cu punctul ideal la dreapta lui x_med voteaza in favoarea lui x_med in raport cu x. Si la fel vor procea, desigur, votantii al caror punct ideal e identic cu x_med. Dar x_med este pozitia mediana, ca urmare exista cel putin ½|G| votanti ale carr puncte ideale sunt ≥ x_med. Ca urmare, x_med primeste cel putin ½|G| voturi, si deci numarul voturilor pentru x_med este mai mare sau egal decat numarul voturilor pentru orice alternativa aflata la sanga sa. Analog se demonstreaza cazul in care x > x_med.

Sa definim acum o relatie intre alternativele de pe agenda in felul urmator: vom spune ca x e median-preferata lui y - si vom scrie P_med(x,y) in acest caz - daca x e mai apropiata de x_med decat y. Cu alte cuvinte, avem:

P_med(x,y) = df. |x - x_med| < |y - x_med|

Acum putem demonstra urmatorul rezultat:

Teorema preferintei mediane. Daca exista o singura dimensiune, preferintele individuale au un singur varf, sunt simetrice si exista o singura pozitie mediana x_med, atunci: x e preferata prin regula majoritatii simple lui y ori de cate ori P_med(x,y).

Demonstratie. Sa observam mai intai ca oricare ar fi pozitiile x si y, media lor aritmetica (x+y)/2 (adica pozitia aflata la egala departare de cele doua pozitii) e mai apropiata de x_med decat atat x cat si y: avem P_med((x+y)/2,x) si P_med((x+y)/2,y). Un exemplu de aranjare posibila a lui x si y fata de x_med e dat in Figura 4 mai jos. Sa ne uitam la ea. Daca o pozitie se afla la dreapta lui (x+y)/2, ea este mai apropiata de x decat de y; daca este la stanga lui (x+y)/2, atunci e mai apropiata de y decat de x. Dar am presupus ca pozitia x_med este unica. Aceasta inseamna ca la dreapta ei se afla cel putin jumatate din punctele ideale ale votantilor. Or, toate aceste puncte se afla la dreapta lui x_med si deci si la dreapta lui (x+y)/2. Cum preferintele sunt simetrice, inseamna ca x primeste majoritatea voturilor in raport cu y.

Figura 4

Cele doua teoreme, a votantului median si a preferintei mediane, au consecinte practice extraordinare. Noi le vom discuta pe larg in capitolul urmator. Aici sa observam doar ca, daca pe agenda publica se discuta sa zicem chestiunea fondurilor care urmeaza sa fie alocate din bugetul public pentru educatie, cetatenii isi vor forma fiecare un punct de vedere si deci fiecare va sustine o anumita pozitie: mai multi sau mai putini bani pentru educatie. Exista o pozitie mediana; ea nu este neaparat, asa cum am vazut, pozitia centrului. Dar, daca - asa cum dorea si Aristotel - societatea devine una in care patura de mijloc este cea mai numeroasa parte a societatii, atunci ea va fi cea centrala. Teoremele demonstrate aici spun ca cetatenii vor prefera sa voteze pentru aceasta alternativa mediana. Si atunci apare consecinta: daca partidele politice doresc sa obtina mai multe voturi, atunci vor trebui sa sustina un punct de vedere cat mai apropiat de pozitia mediana. In general, asa cum remarcase inca Aristotel, puterea se gaseste in "centru". (In ce conditii e adevarata aceasta consecinta vom vedea mai pe larg in capitolul urmator.)

Vom incheia acest capitol cu o scurta discutie referitoare la supozitiile facute aici. Ele sunt, desigur, simplificatoare; dar au rolul de a permite elaborarea unor modele spatiale simple ale alegerilor. Ar fi insa interesant de vazut cum pot fi ele relaxate. De pilda, una dintre supozitiile esentiale facute aici este unidimensionalitatea: exista o singura chestiune in discutie, iar preferintele individuale privesc doar acea chestiune. In exemplul nostru, Consiliul facultatii urma sa decida in privinta taxelor de studii. Dar in cele mai multe situatii grupurile se confrunta in acelasi timp nu cu una, ci cu mai multe probleme. Ce se intampla in aceste cazuri? Sa presupunem ca in Consiliul facultatii se discuta si alte chestiuni, cum ar fi sa zicem cresterea numarului de studenti in anul universitar urmator; sau alocarea unor fonduri mai mari pentru cercetare etc.

Din pacate, rezultatele obtinute sunt, pe de o parte, foarte restrictive: s-a demonstrat ca exista intr-adevar situatii (care satisfac asa-numitele conditii ale lui Plott; cf. Plott: 1967) in care, pentru cazurile in care avem mai multe dimensiuni, se poate defini o teorema a votantului median . Dar situatiile respective sunt de asemenea extrem de rare si de nenaturale. Pe de alta parte, s-a argumentat ca in celelalte situatii se poate intampla orice (teorema haosului a lui McKelvey: 1976): cu alte cuvinte, este posibil orice rezultat al votului - si, in general, votul poate fi manipulat. Asupra acestor chestiuni vom reveni in capitolul urmator.