| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
THE DETERMINATION OF THE RYDBERG CONSTANT
Work purpose
The determination of the constant involved in the spectral series of the hydrogenoid atoms / ions.
Theory
The atoms of each element emit, when they are excited (for instance in an electrical discharge in a gas), an optical discrete spectrum on the basis of which the element can be identified. The spectra of chemical elements are as complicated as their atomic number Z is greater. The optical spectra of the atoms are due to the optical electrons, that is the electrons situated on the peripheral orbitals.
The spectroscopists established that all the lines of different spectral lines of the hydrogenoid atom / ion (a hidrogenoid ion is formed by a nucleus and a single electron) could be described by a general relation, which gives us the wavelength of the spectral lines:
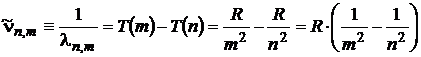 . (1)
. (1)
In the above relation n and m are integer numbers, T(m) and T(n) are spectral terms, and
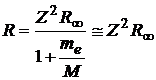 , (2)
, (2)
where ![]() is the electron mass, M is the nucleus mass and
is the electron mass, M is the nucleus mass and ![]() is Rydberg constant.
For hydrogen, this constant becomes the hydrogen Rydberg constant:
is Rydberg constant.
For hydrogen, this constant becomes the hydrogen Rydberg constant:
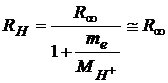 .
(3)
.
(3)
The explanation of the spectral series of the hydrogen atom represented a successful verification of the hydrogen atom theory given by Niels Bohr. Bohr sustains that there are only certain orbits allowed for the electron, corresponding to certain stationary states. He formulated the following postulates:
I. The atom can
exist in a discrete series of stationary states determined by the discrete
series ![]() of the total energy.
In these states the atom does not emit or absorb energy.
of the total energy.
In these states the atom does not emit or absorb energy.
II. The energy
of the atom can change discontinuously, by the transition from one stationary
state of total energy ![]() to another stationary
state of total energy
to another stationary
state of total energy ![]() , with the absorption or emission of a photon. The frequency
of the absorbed or emitted photon is given by the relation:
, with the absorption or emission of a photon. The frequency
of the absorbed or emitted photon is given by the relation:
![]() (4)
(4)
(h being the Planck constant), the process of absorption taking place in the case when the electron passes from a closer orbit to nucleus to a more distant one, and the emission taking place in the opposite case.
The specification of the allowed orbits is obtained by introducing the quantification condition stated by Bohr, who found that the angular momentum of the electron on the allowed orbits must be an integer multiple of ћ:
![]() , (5)
, (5)
where ![]() is the rationalised
Planck constant and n = 1, 2, 3, is called the principal quantum number. The total
energy
is the rationalised
Planck constant and n = 1, 2, 3, is called the principal quantum number. The total
energy![]() , on the n-th orbit
is quantized by the expression:
, on the n-th orbit
is quantized by the expression:
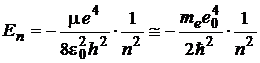 ,
(6)
,
(6)
where
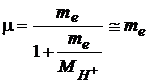 (7)
(7)
is the reduced mass and
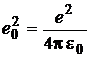 (8)
(8)
is the rationalised elementary
charge (![]() being the vacuum permitivity). In the quantum mechanics, the
electron energy for the hydrogen atom (Eq. (6)) is found by integrating the
Schrdinger equation. The total electron energy on different stationary orbits
is negative, which means that the electron is bound by the electromagnetic
field of the nucleus. Using the relations (4) and (6), one can obtain:
being the vacuum permitivity). In the quantum mechanics, the
electron energy for the hydrogen atom (Eq. (6)) is found by integrating the
Schrdinger equation. The total electron energy on different stationary orbits
is negative, which means that the electron is bound by the electromagnetic
field of the nucleus. Using the relations (4) and (6), one can obtain:
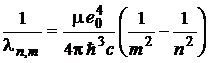 , m,
n = 1, 2, 3, , m < n (9)
, m,
n = 1, 2, 3, , m < n (9)
(c being the speed of light in vacuum) and, comparing this with (1), (3) and (7), it results that:
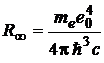 . (10)
. (10)
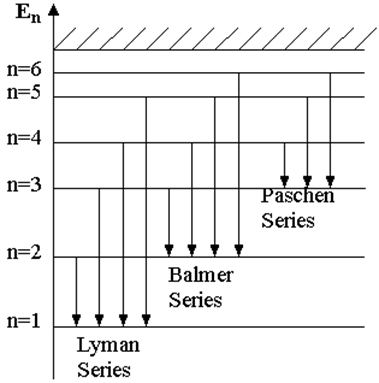
Using Eq. (4),
every wavelength of the lines from different spectral series for hydrogen can
be found. A spectral series represents the sum of spectral lines that have a
common desexcited energetic level (see Figure 1).
Figure 1.
So, there is the Lyman series, which has the common energetic level corresponding to m = 1 (in Eq. (9)), and n 2 and is situated in the ultraviolet range; Balmer series, for which m = 2 and n 3, in the visible range; Paschen series, for which m = 3 and n 4 and the following series, all in the infrared range.
In this experiment we will study
Balmer spectral series and determine the wavelengths for the lines ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() presented in Figure 2.
In the case of Balmer series, the relation (1) becomes:
presented in Figure 2.
In the case of Balmer series, the relation (1) becomes:
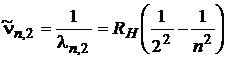 , n = 3, 4, 5, 6, 7, (11)
, n = 3, 4, 5, 6, 7, (11)
from which the
Rydberg constant results:
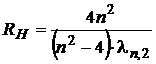 . (12)
. (12)
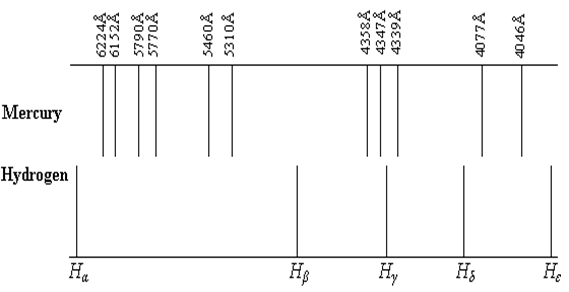
Figure 2.
Experimental set-up
The hydrogen spectrum in the visible band is recorded on a photographic plate (spectrogram), which is set between two plexiglas plates. On the same photographic plate, it appears, parallel to the hydrogen spectrum, the mercury spectrum, used as a comparison spectrum, being recorded at the same spectrograph and in identical conditions.
The mercury spectrum presents a
number of lines, their configuration appearing in Figure 2, on which there are
also indicated the wavelengths corresponding to each spectral line. The lines
of the atomic hydrogen belonging to Balmer series (![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ) whose wavelength we are going to determine, also appear in
Figure 2, in their relative positions with respect to the lines of the mercury
spectrum.
) whose wavelength we are going to determine, also appear in
Figure 2, in their relative positions with respect to the lines of the mercury
spectrum.
We study the spectrogram with a microscope. The microscope bed can be moved horizontally, along two perpendicular directions, using two screws. The movement along the spectrum allows us to measure the position of a spectrum line on a ruler, graduated in mm and with a vernier, the precision being 0.1 mm. To fix the position of desired line the ocular of the microscope has a reticular wire.
To accomplish the work, there are necessary the spectrogram with the visible atomic hydrogen spectrum (Balmer series) and the mercury spectrum, and a microscope.
Working Procedure
Looking through the ocular, adjust the microscope mirror to have the best illumination. If the microscope has a lamp, plug in its transformer. In order not to break the spectrogram, the initial position of the microscope must have the object lens stuck to the spectrogram and then gradually lift, until the spectral lines are clearly visible. Verify the parallelism between the spectral lines and the reticular wire, the parallel setting of the reticular wire being made by rotating the ocular.
Identify the mercury and hydrogen
spectra, looking first at the spectrogram with the naked eye and then at the
microscope. Read on the ruler (after superposing the reticular wire on each
line) the positions ![]() of the mercury lines
(the wavelengths being given for each of them). Read also on the ruler the
positions
of the mercury lines
(the wavelengths being given for each of them). Read also on the ruler the
positions ![]() of the lines from the
hydrogen series (
of the lines from the
hydrogen series (![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ).
).
Draw on a millimetric paper the
calibration curve for the mercury ![]() . Having the positions
. Having the positions ![]() of the hydrogen lines, the wavelengths of the
lines
of the hydrogen lines, the wavelengths of the
lines ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , necessary to compute the Rydberg constant, result from the calibration curve.
, necessary to compute the Rydberg constant, result from the calibration curve.
Experimental data processing
The data measured for mercury are written in Table 1.
Table 1.
|
x (mm) |
|
The measured data for the lines ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are written in Table
2.
are written in Table
2.
Table 2.
Line |
x (mm) |
n |
RH (m-1) |
|
|
| ||||
Compute the Rydberg constant according to the relation (12); the obtained value are written in Table 2.
Compute the mean value
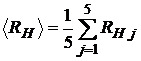 (13)
(13)
and the standard error
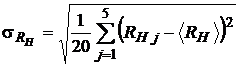 . (14)
. (14)
The final result is presented in the form
![]() . (15)
. (15)
Questions
What is a spectral series?
What is a spectral term?
What postulates lay at the basis of Bohr's formula for the energy levels of the hydrogenoid atoms / ions?
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2083
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved