| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
1. Definition and examples
The notion of vector space constitues the study of linear algebra and represents one of the most important algebraic structures used in different branches of mathematics, as in the applicated disciplines.
|
1.1 Definition |
A non-empty set it is called vector space (linear) over field K (K-vector space) if the following conditions are satisfied : |
|
(V, +) forms an abelian group structure, namely |
a) (x+y)+z = x+(y+z) , x, y, z I V
b)
such that
, x + 0
= 0 + x
c)
,
, x + (-x) = (-x) + x = 0
d)
,
II. The law of external composition K
a) a (x + y) = ax + ay
b) (a + b) x = ax + bx
c) a bx ab) x
d) 1 x = x, a b I K x, y I V
Conditions I and II represent the vector space axioms over field K.
The elements of vector V are called vectors, the elements of field K are called scalars and the external law of composition is called scalars multiplication.
If the commutative corp K is the corp of real numbers R or complex C, we will talk about a real space vector, respectively complex vector space.
Most of the times we will have vector spaces over the real number corp and will call then simple vector spaces', and in the other cases will indicate the scalar field.
If we note with 0V the null vector of the additive group V and with 0K the null scalar, then from the axioms that define the vector space V over field K we have the following properties:
|
1.2 Corollary |
If V is a vector space
over field K, then for, 0K x = 0V a 0V = 0V x= -x . |
Demonstration: 1) Using axioms IIb and IId we have 0K x = (0K + 0K)x = = 0K x + 0K x T 0K x = 0V .
2) Taking into
acount Ib and IIa, a0V = a(0V + 0V)
= a0V + a0V from which we obtain
.
3) from the additive group axioms of field K, the consequence 1) and axiom Ic we have x + (-1)x = [1 + (-1)]x = 0Kx = 0V we obtain (-1) x= -x.
1 Let it be K a commutative corp. Considering the additive abelian structure of field K, then set K represents K-vector space. More, if K' K is a subcorp, then K is a K'-vector space. The set of complex numbers C can be seen as a C-vector space or R-vector space, Q- vector space.
2 The set Kn = K K K, where K is a commutative corp, is K- vector space, called arithmetic space (standard), according to the operations: x,y IV , a I K , x= (x1, x2,..,xn), y = (y1, y2,..,yn)
3 The set matrices of Mm n(K), is a K- vector space with respect to the operations:
The set K[X] of polynoms with coefficients from field K is a K- vector space according with the operations:
f = (a0, a1,..), g = (b1, b2,..) I K[X], a I K.
5 The set of solutions of a linear and homogenous equation system forms a vector space K of the coefficients of this system. The solutions of a system of m equations and n unknown variables, seen as elements from Kn (n-uple), can be summed and multiplied with a scalar respecting the sum and product with scalars defined on Kn.
6 The set of free vectors V3 from the punctual space of elementary geometry is R- vector space.
To build this
set we consider the geometric space E3 and set M = E3 E3 = . The elements of set M are called bipoint or oriented segments and
will be noted with
A C D
B
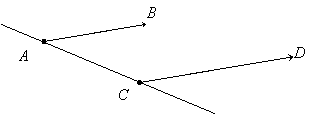
Two non-zero oriented segments
Fig.1
The length
(module or norm) of an oriented segment
On the set M we introduce the equipolent relation '~'.
B C A
D
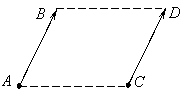
Two oriented segments
It is easy two verify that the equipolent relation is an equivalence relation on set M (is reflexive, symmetric and transitive).
The set of equivalence classes, according to this relation:
M/~ = V
defines the set of free vectors
of the geometric space E3.
The equivalence class of the oriented segment
Two free
vectors
Two free vectors which have the same direction are called colinear vectors. Two collinear vectors with the same length and opposite sense are called oppose vectors.
Three free vectors are called coplanar if their oriented corresponding segments are parallel with a plane.
The set V3 can be organized as an abelian additive group.
A D C
B
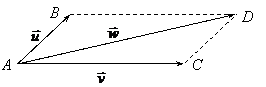
If the free vectors
fig.3
The rule
which defines the sum of two free vectors
The sum of
two free vectors +: V3
V3 V3,
The external composition law
j : K V3 V3,
where the vector
,
oppose sense if
and ||
|
||
In conclusion, the the free vectors set is a real vector space .
2. Vector subspaces
Let it be V a vector space over field K.
|
2.1 Definition. |
A non-empty subset U V is called vector subspace of V if the algebraic operations from V induce on U a structure of K-vector space. |
|
2.2 Theorem. |
If U is a subset of K-vector space V, then the following affirmations are equivalent: 1 U is a vector subspace in V 2 x, yI U, aI K we have a) x + yI U b) axI U x, yI U a b I U T ax + by I U |
Demonstration
1 2:
if U V is a subspace then for
and, because the two operations induce on
subset U a structure of vector space.
2 3:
3 1:
and for a = 1,
b = -1 results that x - y I
U which proves that U V is an abelian subgroup. On the other
side
,
and
and the axioms II from the definition of the
vector space verifies immediately, so the subset U
V posses a structure of vector space.
Example
1 The set V is subspace in V, called nul subspace of V. Any subspace different from the vector space V and the nul subspace is called proper subspace.
2 The set of the symmetric matrices (antisymmetric) of n order is a subspace of the square matrices set of n order.
3 The polynomial set with real coefficients of degree n, R[X] = represents a vector subspace of the vector space of the polynoms with real coefficients.
Subsets
Rx R Ry = R
are vector subspaces of the arithmetic space R2. Generally, the set of the points from any line which passes through the origin of space R2, determine a vector subspace. This vector subspaces represents the solutions set of some linear and homogenous equations in two unknowns.
|
2.3Proposition. |
Let it be V1 and V2
two subspaces in K-vector space V.
The subsets V1 V2
V and V1 + V2 = = |
Demonstration. For
x, y I V1 V2
T
x, y I V1 and
so V1
and V2 are vector
subspaces of V results that for
we have
and
,
so ax + by I V1 V2.
Using Theorem 2.1 results the first part of the proposition.
If
,
and
, q.e.d.
Observation. The subspace V1 V2 V is not an vector space.
Example. The vector subspaces Rx and Ry are defined in exampe 4, it verifies the relations:
Rx Ry = and Rx + Ry = R2.
Indeed, if (x, y) I Rx Ry (x, y) I Rx and (x, y) I Ry y = 0 and x = 0, which proves that subspace Rx Ry is formed only from the nul vector.
For (x, y) I R2 , (x, 0) I Rx , (0, y) I Ry , such that (x, y) = (x, 0) + (0, y) which proves that R2 Rx + Ry. The reverse inclusion is obvious.
|
2.4 Proposition |
Let V1
, V2 V be two vector subspaces and v I
V1 + V2. The decomposiotion |
Demonstration: The necessity of the condition is proved by reduction to absurd. Lets suppose that V1 V2 T v 0 which can be written v = 0 +v or v = v+ 0, which contradicts the unicity of writing, so V1 V2 = .
To prove the
conditions sufficiency we admit that
.
Because
and
,
vector
is contained in V1 V2. For V1 V2 =
results that
and
.
If V1 and V2 are two vector subspaces of the vector space V and V1 V2 = then the sum V1 + V2 is called direct sum and is noted with V1 V2. Plus, if V1 V2 = V, then V1 and V2 are called supplementary subspaces. In case that V1 V is a given vector space and there exists an unique subspace V2 V such that V = V1 V2, then V2 is called the algebraic complement of subspace V1.
Example. Vector subspaces Rx and Ry, satisfying proprieties Rx Ry = , Rx + Ry = R2, are supplementary vector subspaces, and the arithmetic space R2 can be represented under the form R2 = Rx Ry. This fact permits that any vector (x, y) I R2 can be written in an unique way as the sum of the vectors. (x, 0) I R2 and (0, y) I R2, (x, y) = (x, 0) + (0, y).
Observation. The notions of sum and direct sum can be extended to a finite number of terms.
|
2.5 Definition. |
Let it be V a vector space over field K and S a non-zero subset of it. A vector v I V as
is called linear finite combination of elements from S. |
|
2.6 Theorem. |
If S is anon-zero subset of V, then the set of all linear finite combinations of elements from S, is noted L(S) or <S>, is a vectorial subspace of V, called generated subspace by set S or linear covering of S. |
Demonstration Applying the result of theorem 2.1 for
x, y I
L(S), a, b I K,
.
|
2.7 Consequence. |
If V1 and V2 are two vectorial subspaces of vector space V then L(V1 V2)=V1 + V2. |
|
2.8 Definition. |
A subset S V is called generators system for vector space V if the generated subspace by subset S coincides with V, L (S)=V. |
If S subset is finite, and for any vector v I
V,
li I K,
A generalization of the notion of vector space is given by the notion of linear variety.
|
2.9 Definition. |
Is called linear variety in vector space V a subset L V for which exists a vector x I L such that the set |
Subspace VL is called the director subspace of linear variety L.
Lets
consider a line L which passes
through point
.
The point
,
(a, b) I L is situated on a parallel line with L
R which passes through the
origin .
y x b b-b0 V1 L x v a a-a0 0 a0 x0 b0
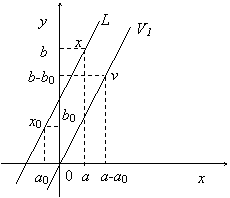
fig.4
In finely, the subset of points from the vector space R2 situated on any line (L) from plane represents a linear variety having as director vector space the line which passes through origin and is parallel with line (L).
A vector subspace represents a particular case of linear variety; is that of linear variety of vector space V which contains the nul vector of the vector space V (v0 = 0).
Let it be V a K-vector space and subset S = V.
|
2.10 Definition. |
The vectors subset S = V is called linearly independent ( free or x1,
x2, , xn are
linear independent) if the equality |
A set(finite or not) of vectors from a vector space is linear independent if any finite system of vectors is a system of linear independent vectors.
|
2.11 Definition. |
The vector subset S = V is called linearly dependent (tied or vectors x1, x2,..,
xn are linear dependent), if ) l1, l2, , lp I K
not all zero, such that |
Remark: If the canceling of a linear finite combination, formed with vectors x1, x2, , xn I V, permits to express a vector in function of others (there exists at least one null coefficient ) then vectors x1, x2, , xp are linear dependent, contrary they are linear independents.
|
2.12 Theorem. |
If S = V is a linear independent set and L(S) The linear covering of S, then for any set of p + 1 elements from L(S) is linear dependent. |
Demonstration. Let it be vectors yi =
The relation l1y1 + l2y2 + +lp+1yp+1 = 0 is equivalent with
are linear independents we obtain for
3. Base and dimension
Let it be V a K-vector space
|
3.1 Definition. |
A subset B (finite or not) of vectors from V is called base of the vector space V if: 1) B is linear independent 2) B represents a system of generators for V. |
The vector space V is called finite generated or finite dimensionally if there exists a finite system of generators.
|
3.2 Theorem. |
If V is a finite generated vector space and S is a system of generators for V, then there exists a base B S of the vector space V. (From any finite system of generators of the vector space it can be extracted a base). |
Demonstration: First, prove that S contains also non-zero vectors. Suppose that S =
, than
can be written as x = l
0 = 0 (S
system of generators) contradiction, so S
.
Let it be now x1 I S a non-zero vector. The set L = S represents a linear independent system. We continue adding non-null vectors from S for which the subset L represents a linear independent set. Lets suppose that S contains n elements, then S has 2n finite subsets. If after a finite number of steps we will find L S, a system of linear independent vectors and for L S with L L, L represents a linear dependent subset (L is maximum in the relation sense order).
L is a
generator system for V. Indeeed, if L = for m = n T L = S and is a system of generators, and if m < n, then
, represents a system of linear
dependent vectors (L is maximal) and
. Results that
|
3.3 Consequence. |
If V and S V a generator finite system and L1 S a linear independent system, then exists a base B of vector space V, such that L1 B S. |
A vector space V is finite dimensional if it has a finite base or if V = , contrary is called dimensional infinite.
Examples
1In arithmetic space Kn the vector subset B=, where e1=, e2=,, en=, represents a base of the vector space Kn, called canonic base.
2 In vector space of polynomswith real coefficients R[X] subset B = , constitutes a base. R[X] is an infinite dimensional space.
|
3.4 Proposition. |
In K-vector space V finite generaedt, any two bases have the same number of elements. |
Demonstration. Lets consider in vector space V finite generated the bases B and B , having card B= n, respective card B = n . Using consequence 3.3 we obtain sequently n n and n n, so n = n.
The last proposition permits the introduction of the dimension notion of a vector space.
|
3.5 Definition. |
Is called dimension of a finite generated vector space, the number of vectors from a base of it noted with dimV. The null space has dimension 0. |
Observation If V is a vector space with dimension dimV = n then:
a) a system of n vectors is base is free independent.
b) a system of n vectors is base is a system of generators.
c) Any system of m > n vectors is linear dependent.
We will note K- n-dimensional vector space with Vn, dimVn = n.
|
3.6 Proposition. |
If B = is a base of K-vector space Vn then any vector x I Vn admits an unique expressions |
Demonstration We suppose that x
I
Vn will have another expression
,
a non-null linear combination of the linear independent vectors of the base,
equivalent with
.
The
scalars l1,
l2,, ln are called the coordinates of vector x in
base B, and the
bijections
,
are called system of coordinates on V.
|
3.7 Theorem. |
(Steinitzexchange theorem). If B = is a base in vector space Vn and S = is a system of linear independent vectors from Vn then p n and after an eventual remuneration of base vectors B the system B = represents also a base for V. |
Demonstration: Applying the result of consequence 3.3 and the fact that any two bases have the same cardinal results that p n.
For the second part of the theorem
we use the method of complete mathematical induction. For p = 1, f1 I V
we write in base B under the form
,
that means that is a system of generated vectors of space Vn, so a base. Admitting that is a base then vector fp I S can be expressed under the form fp = m1f1 + m2f2++ mp-1fp-1+ mpep++ mnen.
In this relation at least one coefficient amongst mp,
mp+1,,
mn is
non-null, because contrary the set S
would be linear dependent. Doing eventual o remuneration of vectors ep,
ep+1, , en,
e can suppose that mp
0 and we obtain
,
from which results that is a system of n generating vectors of n-dimensional space Vn, so a base for Vn,
q.e.d.
|
3.8 Consequence. |
(completing theorem) Any system of linear independent system from a vector space Vn can be completed up to a base in Vn. |
|
3.9 Consequence. |
Any subspace V of a finite generated vectorial space Vn admits at least one suplimentary subspace. |
|
3.10 Theorem. |
(Grassmann dimension theorem). If V1 and V2 are two vectorial subspaces of K-vector space Vn then |
din (V + V ) = dimV dimV dim(V1 V (3.1)
Demonstration: Let it be a base of subspace (V1 V2) V1.
From the consequence 3.8 we can complete this system of linear independent vectors at a base in V1 , this is given by set B . In a similar way we consider in vector space V2, base B . It is easy to demonstrate that the subset B , is a system of generators for V1+ V2. The subset B is linear independent. Indeed,
which means
that vector
Using this result in the first relation and with respect to the fact that B1 is a base in V1 resultsa1 = a2 = = ar = b r+1 = b r+2 = = 0, so B is linear independent, is a base in V1+V2.
In these conditions we can write dim (V1+V2) = r + s + p = = (r +s) + (r + p) r = dimV1 + dimV2 - dim(V1 V2). Q.e.d.
|
3.11 Consequence. |
If the vector space Vn is represented under the form V1 = V1 V2 then dimVn = dimV1 + dimV2. |
Lets consider a K-vector space Vn and B = respective B = two bases in Vn. Any vector from B can be expressed in function of the elements of the other base. So we have the relations:
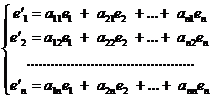
Noting with B = t[e1,
e2,, en], B = t[e 1,
e 2,, e n] and with
B = tAB (3.2)
Let it be now a vector x I Vn, expressed in the two bases of the vector space Vn through relations:
With respect to relations (4.2), we obtain
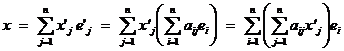
With B is a base, the equality
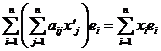
relations which characterize the transforming of a vectors coordinates to a change of the vector space base Vn .
If we note with X = t[x1, x2,,xn] the column matrix of the vectors coordinates x I Vn in baza B and respective with X = t[x 1, x 2,,x n], the coordinate matrix of the same vector x I Vn in baseB , we can write
X = AX (3.4)
Matrix A = (aij) is called passing matrix from base baza B to base B . In conclusion, in a finite dimensional vector space we have the change of base theorem:
|
3.12 Theorem. |
If in vector space Vn, the change of base B with baseB is given by relation B = tAB, then the relation between the coordinates of a vector x I Vn, in the two bases ,is given by X = AX . |
Let it beVn
a vector space and B = a base of his. If the
vectors v1, v2,, vp I Vn, p
n are expressed through the relations vj =
|
3.13 Theorem. |
The matrix rang A is equal with the maximum numbers of column linear independent vectors |
Demonstration. Lets suppose that the rang A = r, that means
D
=
D 0 implies that the vectors linear independence v1, v2, , vr.
Let it be column vk, r k p and the determinants
Di
=
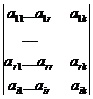
Each one of this determinants is null because for i r, Di has two identical lines, and for i > r, the order of Di is greater then the rang r. Developing after the last line we have:
ai1Γi1 +ai2 Γi2 +air Γir + ail D = 0
This scalar relations express the fact that any column vk, r k p, is a linear combination of the first r columns of matrix A, so any r + 1 vectors are linear dependents.
|
3.14 Consequence. |
If B = is a base in Vn ,then the set B = , |
Let it be V and W two vector spaces over field K.
|
3.15 Definition. |
An application T : V W with proprieties: T (x + y) = T(x) + T(y), x, y I V T ax aT (x) , x I V a I V Is called vector space morphism or linear transformation. |
A bijective linear transformation between two vector spaces will be called vector spaces isomorphism.
|
3.16 Theorem. |
Two vector spaces V and W over firld K, of finite dimension, are called isomorphism if and only if they have the same dimension. |
A
system of coordinates on a finite dimensional vector space Vn, f : V Kn , x I Vn
4. Euclidiene vector spaces
Let it be V a real vector space.
If we add, beside the vector space structure, the notion of scalar product, then in a vector space can be defined notions of vector length, the angle of two vectors, ortoghonality a.o.
|
4.1 Definition. |
An application g: V V R, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a) |
x, y, z I V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b) <l x, y> = l <x, y> |
x, y I V, l I R | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c) <x, y> = <y, x> |
x, y I V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d) <x, x> 0, <x, x> = 0 x = 0 |
, x I V |
is called scalar product on vector space V.
1) <x + y, z> = <x, z> + <y, z> 2) <x, ly> = l <x, y>, x, y, z I V l I R
<x, y>2 <x, x> <y, y> (4.1) the equality having place if and only if vectors x si y are linear dependents. Demonstration: If x = 0 or y = 0 then we have the equality fro relation 5.1. Lets
suppose x and y 0 <z, z> = <lx + my, lx + my> = l2 <x, x> + 2lm <x, y> + m2 <y, y>, equality having place for z = 0. If we take l = <y, y> > 0 then we obtain <x, x> <y, y> + 2lm<x, y> + m2 0, and for m = - <x, y> inequality becomes <x, x> <y, y> - <x, y>2 0, q.e.d Example1 In arithmetic space Rn for any two elements x=(x1,x2,,xn) and y = (y1, y2,, yn), the operation <x, y> =: x1y1 + x2y2 ++ xnyn (4.2) define a scalar product. The scalar product defined in this way, called usual scalar product, endowedrithmetic space Rn with an Euclidean structure. 2 The set C([a, b]) of continuous functions on the interval [a, b] is a vector space with respect to the product defined by
Demonstration: Conditions a) and b) result immediately from the norm definition and the scalar product properties. Axiom c) results using Cauchy-Schwarz inequality
from where results the triangle inequality. A space on which we have defined a norm function is called normed space. The norm defined by a scalar product is called euclidean norm. Example: In arithmetic space Rn the norm of a vector x = (x1, x2,xn) is given by A vector e I V is called versor if ||e|| = 1. The notion of versor permits to x I V to be written as Cauchy-Schwarz inequality, |<x, y>| ||x|| ||y|| permits to define the angle between two vectors, being the angle q I [0, p], given by
Example: In vector arithmetic space Rn the distance d is given by
An ordinary set endowed with the distance is called the metric space. If the norm defined on vector space V is euclidean then the defined distance by this is called euclidean metric. In conclusion, any euclidean space is a metric space. An euclidean structure on V induces on any subspace V V an euclidean structure. The scalar product defined on a vector space V permits the introduction of ortoghonality notion.
A set S V is said to be ortoghonal if its vectors are ortoghonal two by two. An ortoghonal set is called orthonormate if every element has its norm equal with his unit.
Demonstration Let it be S V and l1x1 + l2x2
++ lnxn,
a linear ordinary finite combination of
elements from S. Scalar multiplying
with xj I S, the relation S being orthogonal, <xi, xj> = 0,
i
j and lj(xj, xj) = 0. For xj
0,
If in euclidean vector space Vn we consider an orthogonal base B = , then any vector x I Vn can be written in an unique way under the form
Indeed, multiplying the vector If B is orthonormate we have
Demonstration: If y1, y2 I S then (y1, x) = 0, <y2, x> = 0, x I S. For a b I R, we have <ay by , x> = a<y1, x> + b<y2, x> = 0, c.c.t.d.
Let it be Vn a finite dimensional euclidean vector space.
Demonstration First we build an orthogonal set and then we norm every element. We considerw1 = v1 , w2 = v2 + kw1 0 and determine k imposing the condition <w1, w2> = 0. We obtain w3 = v3 + k1w1 + k2w2 0 and determine the scalars k1, k2 imposing condition w3 to be orthogonal on w1 and w2, that means that <w3, w1> = <v3, w1> + k1 <w1, w1> = 0 <w3, w2> = <v3, w2> + k2 <w2, w2> = 0. We obtain
After n steps are obtained vectors w1, w2, , wn orthogonal two by two, linear independent (prop. 5.1) given by Define With elements e1, e2, , ep are expressed in function of v1, v2, , vp, and these are linear independent subsystems we have L () = = L (), c.c.t.d.
Let it be B = and B = two orthonormate base in euclidean vector space Vn. The relations between the elements
of the two bases are given by With B being orthonormata we have :
If A = (aij) is the passing matrix from base B to B then the anterior relations are the form tAA = In, so A is an orthogonal matrix.
5. Proposed problems 1. Let it be V and W two K-vector spaces. Show that V W = = is a K-vector space with respect to the operations: (x1, y1) + (x2, y2) =: (x1 + x2, y1 + y2) a (x, y) =: (a x, a y x , x2 I V, y1, y2 I W a I K 2. Say if the operations defined on the indicated sets determine a vector space structure:
. Let it be V a real vector space. We define on V V the operations:
Show that V V is a vector space over complex number field C (this space will be called the complexificate of V and will be noted with CV ) . Establish which of the following subsets forms vector subspaces in the indicated vector spaces a) S b) S c) S d) S4 = e) S5 = 5. Let it be F[a,b] the real functions set defined on the interval [a, b] R. a) Show that the operations: (f + g)(x) = f(x) + g(x) (a f)(x) = a f(x), a I R, x I [a, b] define a structure of R-vector space on set F [a,b]. b) If the interval [a, b] R is symmetric with the origin, show that the subsets F+ = (odd functions) and F- = (even functions) are vector subspaces and F [a,b] = F + F - . 6. Show that the subsets S = (symmetric matrix) A = (antisymmetric matrix) Are vectorial subspaces and Mn (K) = S A. 7. Let it be v1, v2, v3 I V, three linear independent vectors. Determine a I R such that the vectors
to be linear independents, respective linear dependents. 8.Show that the vectors x,y,zIR3, x = (-1,1,1), y = (1,1,1), z = (1,3,3), are linear dependent and find the relation linear dependence. 9. Establish the dependence or linear independence of vectors systems: a) S1 = b) S2 = c) S3 = 10) Determine the sum and intersection of the vector subspaces U, V R3, where U = V = 11) Determine the sum and intersection of the subspaces generated by the vectors systems: U V = ) Determine the subspaces U V R where U V = L() ) Determine a base in subspaces U + W, U W and verify the Grassmanns theorem for a)
b)
) Let it be the subspace W1 R generated by vectors w1 = (1,-1,0) and w2 = (-1,1,2). Determine the suplementary subspace W2 and decomposedescompuna vector x = (2, 2, 2) on the two subspaces. ) Show which of the following vectors systems forms bases in the given vector spaces: a) S1 = R2 b) S R c) S3 = R3 d) S4 = R3[x] e)
S5
= ) In R3 we consider the vectors systems B = and B = . Show that B and B are bases and determinethe passing matrix from base B to base B and the coordinates of the vector v = (2, -1, 1) (expressed in canonic base) in rapoert with the two bases. 17) Let it be the real vector space M2(R) and the canonic base B = a) Find a base B respective B in the symmetric matrices subspace S2 M2(R) and respective in the antisymmetric matrices subspace A2 M2(R). Determine the passing matrices from the canonic base B to base B = B B . b)
Express the matrix E = 18) Verify if the following operations define scalar products on the considerated vector spaces a) <x, y> = 3x1y1 + x1y2 + x2y1 + 2x2y2 , x = (x1,x2), y = (y1, y2) I R b) <x, y> = x1y1 - 2x2y2 , x = (x1, x2), y = (y1, y2) I R c) <x, y> = x1y1 + x2y3 + x3y2 , x = (x1, x2, x3), y = (y1, y2, y3) I R 19) Show that the operation defined on
the polynoms set Rn[x] through
<f, g> = 20) Verify that the following operations determine scalar products on the specificated vector spaces and orthonormate with respect to these scalar products the functions systems and respective a)
<f,
g> = b)
<f,
g> = 21) Let it be vectors x = (x1, x2, , xn), y = (y1, y2, , yn) I Rn. Demonstrate using the usual scalar product defined on the arithmetic space Rn, the following inequalities: a)
b)
and determine the conditions in which take place the equalities. 22) Orthonormate the vectors system with respect to the usual scalar product a) v1 = (1, -2, 2), v2 = (-1, 0, -1), v3 = (5, 3,-7) b) v1 = (1, 1 , 0), v2 = ( 1, 0, 1 ) , v3= (0, 0, 1) . 23) Find the orthogonal projection of vector v = (14, -3, -6) on the subspace generated by vectors v1 = (-3, 0, 7), v2 = (1, 4, 3) and the size of this projection. 24) Determine in the arithmetic space R3, the orthogonal complement of the vector subspace of the systems solutions
and find an orthonormate base in this complement. 25) Orthonormate the following linear independent vector systems: a) v = (1, 1, 0), v2 = (1, 0, 1), v3 = (0, 0, -1) in R3 b) v = (1,1,0,0), v2 = (1,0,1,0), v3 = (1,0,0,1), v4 = (0,1,1,1) in R4. 26) Determine the orthogonal complement of the subspaces generated by the following vectors system: a) v = (1, 2, 0), v2 = (2, 0, 1) in R3 b) v = (-1, 1, 2, 0), v2 = (3, 0, 2, 1), v3 = (4, -1, 0, 1) in R4 ) Find the vectors projection v = (-1, 1, 2) on the solution subspace of the equation x + y + z = 0. ) Detremine in R3 the orthogonal complement of the subspace generated by vectors v1 = (1, 0, 2), v2 = (-2, 0, 1). Find the decomposition v = w + w1 of vector v = (1, 1, 1) I R on the two complementary subspaces and verify the relation ||v||2 = ||w||2 + ||w1||2.
DISTRIBUIE DOCUMENTUL
Comenteaza documentul:Te rugam sa te autentifici sau sa iti faci cont pentru a putea comentaCreaza cont nou Termeni si conditii de utilizare | Contact
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
is unique if and only if V1 V2 =
.
,
, happens only if 
.
.
