| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
As it is known, matter and therefore fluid bodies as well, has a discrete and discontinuous structure, being made up of micro-particles (molecules, atoms, etc) that are in reciprocal interaction.
The mechanics of fluids studies phenomena that take place at a macroscopic scale, the scale at which fluids behave as if matter were continuously distributed.
At the same time, fluids dont have their own shape so are easily deformed.
A continuous medium is homogenous if at a constant temperature and pressure, its density has only one value in all its points.
Lastly, a continuous homogenous medium is isotropic as well if it has the same proprieties in any direction around a certain point of its mass.
In what follows we shall consider the fluid as a continuous, deforming, homogeneous and isotropic medium.
We shall analyse some of basic physical proprieties of the fluids.
Compressibility represents the property of fluids to modify their volume
under the action of a variation of pressure. To evaluate quantitatively this
property we use a physical value, called isothermal compressibility
coefficient, ![]() , that is
defined by the relation:
, that is
defined by the relation:
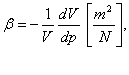 (2.1)
(2.1)
in which dV represents the elementary variation of the initial volume, under the action of pressure variation dp.
The coefficient ![]() is intrinsic positive; the minus sign that
appears in relation (2.1) takes into consideration the fact that the volume and
the pressure have reverse variations, namely dv/ dp < 0.
is intrinsic positive; the minus sign that
appears in relation (2.1) takes into consideration the fact that the volume and
the pressure have reverse variations, namely dv/ dp < 0.
The reverse of the isothermal compressibility coefficient is called the elasticity modulus K and is given by the relation:
![]() (2.2)
(2.2)
Writing the relation (2.2) in the form:
![]() (2.3)
(2.3)
we can underline its analogy with Hooks law:
![]() (2.4)
(2.4)
a) The compressibility of liquids
In
the case of liquids, it has been experimentally ascertained that the elasticity
modulus K, and implicitly, the coefficient ![]() , vary very
little with respect to temperature (with approximately 10% in the interval
, vary very
little with respect to temperature (with approximately 10% in the interval ![]() ) and they
are constant for variations of pressure within enough wide limits. In table (2.1)
there are shown the values of these coefficients for various liquids at
) and they
are constant for variations of pressure within enough wide limits. In table (2.1)
there are shown the values of these coefficients for various liquids at ![]() and pressure
and pressure ![]() bars.
bars.
Table 2.1.
|
Liquid |
|
|
|
Water |
|
|
|
Petrol |
|
|
|
Glycerine |
|
|
|
Mercury |
|
|
Therefore,
in the case of liquids, coefficient ![]() may be considered constant.
may be considered constant.
Consequently,
we can integrate the differential equation (2.2) from an initial state,
characterised by volume ![]() , pressure
, pressure ![]() and density
and density ![]() to a certain final state, where the state parameters
will have the value
to a certain final state, where the state parameters
will have the value ![]() and
and ![]() respectively; we shall successively get:
respectively; we shall successively get:
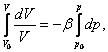 (2.5)
(2.5)
or
![]() (2.6)
(2.6)
b) The compressibility of gases
For gases the isothermal compressibility coefficient depends very much on pressure. In the case of a perfect gas, the following relation describes the isothermal compressibility:
pV = cons.,
which, by subtraction, will be:
![]() (2.8)
(2.8)
By comparing this relation to (2.3) we may write:
![]() (2.9)
(2.9)
It follows that, in the case of a perfect gas, the elasticity modulus is equal to pressure.
Thermal dilatation represents the fluid property to modify its volume under the action of a variation of temperature. Qualitatively, this property is characterised by the volumetric coefficient of isobaric dilatation, defined by the relation:
![]() (2.10)
(2.10)
where
dV represents the elementary variation of the initial volume V under the action
of variation of temperature dT. Coefficient ![]() is positive for all fluids, except for water,
which registers maximum density (minimum specific volume) at
is positive for all fluids, except for water,
which registers maximum density (minimum specific volume) at ![]() ; therefore,
for water that has
; therefore,
for water that has ![]() we shall have
we shall have ![]()
Generally,![]() varies very
little with respect to temperature, therefore it can be considered constant.
Under these circumstances, integrating the equation (2.10) between the limits
varies very
little with respect to temperature, therefore it can be considered constant.
Under these circumstances, integrating the equation (2.10) between the limits ![]() and V, and respectively
and V, and respectively ![]() and T, we get:
and T, we get:
![]() (2.11)
(2.11)
or else
![]() (2.12)
(2.12)
By dividing the relation (2.12) to the mass of the fluid ![]() we get the
function of state for an incompressible fluid:
we get the
function of state for an incompressible fluid:
![]() (2.13)
(2.13)
In the case of a perfect gas the value of the coefficient is obtained by
subtracting the equation of isobaric transformation ![]() ; we get:
; we get:
![]() (2.14)
(2.14)
which, replaced into (2.10) enables us to write:
![]() (2.15)
(2.15)
Thus, for the perfect gas, coefficient ![]() is the reverse of the thermodynamic
temperature.
is the reverse of the thermodynamic
temperature.
In the case of fluids, the molecular cohesion forces have very low values, but they arent rigorously nil.
At a macroscopic scale, this propriety can be rendered by the fact that two particles of fluid that are in contact, can be separated under the action of some very small external forces. At the same time, fluid particles can slide one near the other and have to overcome some relatively small tangent efforts.
As a result, from a practical point of view, fluids can develop only compression efforts.
In the case of a deformation at a constant volume, the compression efforts are rigorously nil and, as a result, the change in shape of the fluid requires the overcoming of the tangent efforts, which are very small. Therefore the mechanical work consumed from the exterior will be very small, in fact negligible.
We say that fluids have a high mobility, meaning that they have the property to take the shape of the containers in which they are. Consequently we should stress that gases, because they dont have their own volume, have a higher mobility than liquids (a gas inserted in a container takes both the shape and the volume of that container).
Viscosity is the property of the fluid to oppose to the relative movement of its particles.
As it has been shown, overcoming some small tangent efforts that arent yet rigorously nil makes this movement.
To qualitatively stress these efforts, we consider the unidimenssional flow of a liquid, which takes place in superposed layers, along a board situated in xOy plane (fig.2.1).
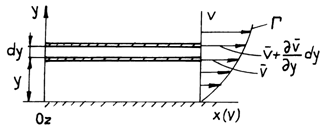
Fig.2.1.
Experimental measurements have shown that velocity increases as we move
away from the board in the direction of axis Oy, and it is nil in the near
vicinity of the board. Graphically, the dependent ![]() is represented by the curve
is represented by the curve ![]() . This
simple experiment stresses on two aspects, namely:
. This
simple experiment stresses on two aspects, namely:
the fluid adheres on the surface of the solid body with which it comes into contact;
inside the fluid and at its contact with the
solid surfaces, tangent efforts generate which determine variation in velocity.
Thus, considering two layers of fluid, parallel to the plane xOy and that are
at an elementary distance dy one from the other, we shall register a variation
in velocity ![]() , due to the
frictions that arise between the two
layers.
, due to the
frictions that arise between the two
layers.
To determine the friction stress, Newton used the relation:
![]()
![]() (2.16)
(2.16)
that
today bears his name. This relation that
has been experimentally verified by Coulomb, Poisseuille and Petrov shows that
the friction stress ![]() is proportional to the gradient of velocity.
The proportionality factor
is proportional to the gradient of velocity.
The proportionality factor ![]() is called dynamic viscosity.
is called dynamic viscosity.
If we represent graphically the dependent ![]() we shall get the line 1 (fig.2.2) where
we shall get the line 1 (fig.2.2) where ![]() .
.
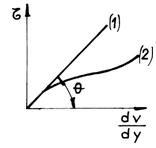
The fluids that observe the friction law (2.16) are called Newtonian fluids (water, air, etc). The dependent of the tangent effort to the gradient of velocity is not a straight line (for example curve (2) in fig. 2.2), for a series of other fluids, generally those of organic nature. These fluids are globally called non-Newtonian fluids.
Fig.2.2
The measures for the dynamic viscosity are:
in the international standard (SI):
![]() (2.17)
(2.17)
in the CGS system:
![]() (2.18)
(2.18)
The measure of dynamic viscosity in CGS system is called poise, and has the symbol P. We can notice the existence of relation:
![]() . (2.19)
. (2.19)
We can determine the dynamic viscosity of liquids with the help of Hpplers viscometer, whose working principle is based on the proportionality of dynamic viscosity to the time in which a ball falls inside a slanting tube that contains the analysed liquid.
The kinematic viscosity of a fluid is the ratio of dynamic viscosity and its density:
![]() (2.20)
(2.20)
The measures for kinematic viscosity are:
in the international system:
![]() (2.21)
(2.21)
in CGS system:
![]() (2.22)
(2.22)
the latter bearing the name stokes (symbol ST):
![]() (2.23)
(2.23)
Irrespective of the type of viscometer used (Ubbelohde, Vogel-Ossag, etc) we can determine the kinematic viscosity by multiplying the time (expressed in seconds) in which a fixed volume of liquid flows through a calibrated capillary tube, under normal conditions, constant for that device.
In actual practice, the conventional viscosity of a fluid is often used; this value is determined by measuring the time in which a certain volume of fluids flows through a special device, the conditions being conventionally chosen. The magnitude of this value thus determined is expressed in conventional units. There are several conventional viscosities (i.e. Engler, Saybolt, Redwood etc) which differ from one another both in the measurement conditions and in the measure units.
Thus, Engler conventional viscosity, expressed in Engler degrees ![]() is the ratio between the flow time of 200
cubic cm of the analysed liquid at a given temperature and the flow time of a
same volume of distilled water at a temperature of
is the ratio between the flow time of 200
cubic cm of the analysed liquid at a given temperature and the flow time of a
same volume of distilled water at a temperature of ![]() , through an
Engler viscometer under standard conditions.
, through an
Engler viscometer under standard conditions.
The viscosity of a fluid depends to a great extent on its temperature. Generally, viscosity of liquids diminishes with the increase in temperature, while for gas the reverse phenomenon takes place.
The dependence of liquids viscosity on temperature can be determined by using Gutman and Simons relation:
![]() (2.24)
(2.24)
where the constants B and C depend on the nature of the analysed liquid (for water we have B= 511,6 K and C= -149,4 K).
For gases we can use Sutherlands formula
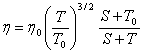 (2.25)
(2.25)
where S depends on the nature of the gas (for air S=123,6 K).
In relations (2.24) and (2.25), ![]() and
and ![]() are the dynamic viscosities of the fluid at
the absolute temperature T, and at temperature
are the dynamic viscosities of the fluid at
the absolute temperature T, and at temperature ![]() respectively.
respectively.
In table 2.2 there are shown the dynamic and kinematic viscosities of air and water at different temperatures and under normal atmospheric pressures.
|
Temperature
| |||||||||
|
|
Air | ||||||||
|
Water | |||||||||
|
|
Air | ||||||||
|
Water | |||||||||
We must underline the fact that viscosity is a property that becomes manifest only during the movement of liquids.
A fluid for which viscosity is rigorously nil is called a perfect or ideal fluid.
Fluids
may be compressible ![]() or incompressible (
or incompressible (![]() is constant
with respect to pressure).
is constant
with respect to pressure).
We should emphasise that the ideal compressible fluid is analogous to the ideal (or perfect) gas, as defined in thermodynamics.
The movement of fluids may be uniform (velocity is constant), permanent v = v (x,y,z) or varied v = v (x,y,z,t).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1400
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved