| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
We
shall further study, for the most
general case, the movement state of a fluid through a volume ![]() that is situated in the fluid stream; we shall
not take into consideration the interior frictions(i.e.viscosity), so we shall
analyse the case of perfect (ideal) fluids that are on varied movement.
that is situated in the fluid stream; we shall
not take into consideration the interior frictions(i.e.viscosity), so we shall
analyse the case of perfect (ideal) fluids that are on varied movement.
The
volume ![]() is situated
in an accelerated system of axes, joint with this system. The equations, which
describe the movement of the fluid, will be obtained by applying dAlemberts
principle for the fluid that is moving through the volume
is situated
in an accelerated system of axes, joint with this system. The equations, which
describe the movement of the fluid, will be obtained by applying dAlemberts
principle for the fluid that is moving through the volume ![]() .
.
The
three categories of forces that act upon the fluid that is moving through the
volume ![]() ,bordered by
the surface
,bordered by
the surface ![]() (fig.3.1), are:
(fig.3.1), are:
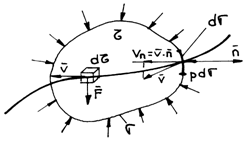
Fig.3.1
the mass forces ![]() ;
;
the inertia forces ![]() ;
;
the pressure forces ![]() (with an equivalent effect; these forces
replace the action of the negligible fluid outside volume
(with an equivalent effect; these forces
replace the action of the negligible fluid outside volume ![]() ).
).
According to dAlemberts principle, we shall get:
![]() (3.1)
(3.1)
Equation (3.1) represents in fact the general vectorial form of Eulers equations.
Lets establish the mathematical expressions of those three categories of forces.
If ![]() is the mass unitary force (acceleration) that
acts upon the fluid in the volume
is the mass unitary force (acceleration) that
acts upon the fluid in the volume ![]() , the mass
elementary force that acts upon the mass
, the mass
elementary force that acts upon the mass![]() , will be:
, will be:
![]() (3.2)
(3.2)
hence:
![]() (3.3)
(3.3)
As
the fluid velocity through the volume ![]() is a
vectorial function with respect to point and time:
is a
vectorial function with respect to point and time: ![]() , upon the
mass
, upon the
mass ![]() that is moving with velocity
that is moving with velocity ![]() the elementary inertia will act:
the elementary inertia will act:
![]() (3.4)
(3.4)
So, the inertia will be:
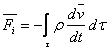 (3.5)
(3.5)
If ![]() is a surface element upon which the pressure p
acts, and
is a surface element upon which the pressure p
acts, and ![]() - the versor
of the exterior normal (Fig.3.1), the elementary force of pressure is:
- the versor
of the exterior normal (Fig.3.1), the elementary force of pressure is:
![]() (3.6)
(3.6)
Having in mind Gauss-Ostrogradskis theorem, the resultant of pressure forces will be:
![]() (3.7)
(3.7)
By replacing equations (3.3), (3.5) and (3.7) in the equation (3.1), we shall get:
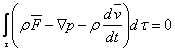 (3.8)
(3.8)
Hence:
![]() (3.9)
(3.9)
Or
![]() (3.10)
(3.10)
The equation (3.10) Eulers equation in a vectorial form for the ideal fluid in a non-permanent movement.
Projecting this equation on the three axes, we shall obtain:
![]()
![]() (3.11)
(3.11)
![]()
This
equation can be obtained by writing in two ways the variation in the unity of
time for the mass of fluid that is in the control volume ![]() , bordered
by the surface
, bordered
by the surface ![]() (fig.3.1). By splitting from the volume
(fig.3.1). By splitting from the volume ![]() one element
one element ![]() , and taking
into consideration that the density is a scalar function of point and time,
, and taking
into consideration that the density is a scalar function of point and time, ![]() , we can
write the total mass of the volume
, we can
write the total mass of the volume ![]() :
:
![]()
The variation of the total mass in the unity of time will be:
![]()
The
second form of writing the variation of mass is obtained by examining the flow
of the mass through surface ![]() that borders volume
that borders volume![]() .
.
Denoting
by ![]() the versor
of the exterior normal to the area element
the versor
of the exterior normal to the area element ![]() , and by
, and by ![]() the vector of the fluid velocity, the
elementary mass of fluid that passes in the unity of time through the area
element
the vector of the fluid velocity, the
elementary mass of fluid that passes in the unity of time through the area
element ![]() is:
is:
![]()
In the unity of time through
the whole surface ![]() will pass,
the mass:
will pass,
the mass:
![]()
that
is the sum of the inlet and outlet mass in volume ![]() , by
crossing surface
, by
crossing surface ![]() .
.
By equalling equations (3.13) and (3.15), it will result:
![]() (3.16)
(3.16)
According to Gauss-Ostrogradskis theorem:
![]()
Taking into consideration (3.17), the equation (3.16) will take the form:
![]() (3.18)
(3.18)
hence, successively:
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
![]() (3.21)
(3.21)
The equation (3.21) represents the equation of continuity for compressible fluids.
In
the case of non-compressible fluids (![]() ,
, ![]() ), the
equation of continuity takes the form:
), the
equation of continuity takes the form:
![]() (3.22)
(3.22)
or
![]() (3.23)
(3.23)
It follows that the inlet volume of
non-compressible liquid is equal to the outlet one in and from the volume ![]()
From a thermodynamically point of view, the state of a system can be determined by the direct measurement of some characteristic physical values, that make up the group of state parameters (e.g. pressure, volume, temperature, density etc.).
Among the state parameters of a thermodynamically system generally there are link relationships, explained by the laws of physics.
In the case of homogenous systems, there is only one implicit relationship, which carries out the link among the three state parameters, in the form of:
![]() . (3.24)
. (3.24)
Adding
to vectorial equations (3.10) and (3.21) the equation of state, we get three
equations with three unknowns ![]() , that
enable us solve the problems of motion and repose for the ideal fluids.
, that
enable us solve the problems of motion and repose for the ideal fluids.
Bernoullis equation is obtained by integrating Eulers equation written under a different form (Euler Lamb), that stresses the rotational or non-rotational nature of the ideal fluid (see the relation (1.25)).
Euler Lambs equation:
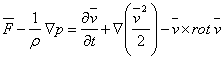 . (3.25)
. (3.25)
Considering the case when the mass force derives from a potential U, thus being a conservative force (the mechanical energy-kinetic and potential-will be constant):
![]() . (3.26)
. (3.26)
In the
case of compressible fluids, when ![]() , we insert
the function:
, we insert
the function:
![]() . (3.27)
. (3.27)
Thus:
![]() . (3.28)
. (3.28)
The equation (3.25) takes the form:
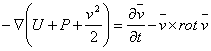 . (3.29)
. (3.29)
The equation (3.29) can be easily integrated in certain particular cases.
In the
case of permanent motion ![]() , and:
, and:
along a stream line:
![]() , (3.30)
, (3.30)
along a whirl line:
![]() , (3.31)
, (3.31)
in the case of potential motion ![]() :
:
![]() , (3.32)
, (3.32)
-in the case of helicoid motion
(the velocity vector ![]() is parallel to the whirl vector):
is parallel to the whirl vector):
![]() . (3.33)
. (3.33)
Multiplying by ![]() the equation (3.29), we shall get under the
conditions of permanent motion (
the equation (3.29), we shall get under the
conditions of permanent motion (![]() ):
):
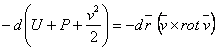 . (3.34)
. (3.34)
Since ![]() , we shall get:
, we shall get:
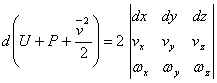 . (3.35)
. (3.35)
The determined is zero for one of the four cases above. By integrating in these cases we shall get Bernoullis equation:
![]() . (3.36)
. (3.36)
If the fluid is a non-compressible one then ![]() .
.
If the axis Oz of the system is vertical, upwards directed, the potential U is:
![]() . (3.37)
. (3.37)
It results the well known Bernoullis equation as the load equation:
![]() . (3.38)
. (3.38)
The
kinetic load ![]() represents the height at which it would rise
in vacuum a material point, vertically and upwards thrown, with an initial
velocity v, equal to the velocity of the particle of liquid considered.
represents the height at which it would rise
in vacuum a material point, vertically and upwards thrown, with an initial
velocity v, equal to the velocity of the particle of liquid considered.
The
piezometric load ![]() is the height
of the column of liquid corresponding to the pressure p of the particle of
liquid.
is the height
of the column of liquid corresponding to the pressure p of the particle of
liquid.
The position load z represents the height at which the particle is with respect to an arbitrary chosen reference plane.
Bernoullis equation, as an equation of loads, may be expressed as follows: in the permanent regime of an ideal fluid, non-compressible, subjected to the action of some conservative forces, the sum of the kinetic, piezometric and position loads remains constant along a streamline.
Multiplying (3.38) by ![]() we get the equation of pressures:
we get the equation of pressures:
![]() , (3.39)
, (3.39)
where:
![]() dynamic pressure;
dynamic pressure;
![]() piezometric
(static) pressure;
piezometric
(static) pressure;
![]() position pressure.
position pressure.
Multiplying (3.38) by the weight of the fluid G, we get the equation of energies:
![]() (3.40)
(3.40)
where
![]() - kinetic energy;
- kinetic energy;
![]() - pressure
energy;
- pressure
energy;
![]() - position
energy.
- position
energy.
Going back to the relation (3.38) and considering C = H (fig.3.2):
![]() (3.41)
(3.41)
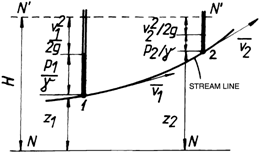
Fig.3.2
The sum of all the terms of Bernoullis equation represents the total energy (potential and kinetic) with respect to the unit of weight of the moving liquid.
This energy measured to a horizontal reference plane N-N, arbitrarily chosen is called specific energy and it remains constant during the permanent movement of the ideal non-compressible fluid that is under the action of gravitational and pressure forces.
Lets consider the flow of an ideal non-compressible
fluid through the channel between two concentric pipes that revolve around an
axis Oz with angular velocity ![]() (fig.3.3.).
(fig.3.3.).
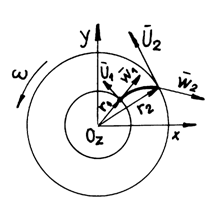
Fig.3.3
In the equation (3.38) v is replaced
by w, which represents the relative velocity of the liquid to the channel that
is revolving with the velocity ![]() .
.
Upon the liquid besides the
gravitational acceleration g, the acceleration ![]() acts as well.
acts as well.
The unitary mass forces decomposed on the three axes will be:
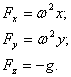 (3.42)
(3.42)
In this case, the potential U will be:
![]() (3.43)
(3.43)
By adding (3.43) to Bernoullis equation, we get:
![]() (3.44)
(3.44)
or
![]() (3.45)
(3.45)
In the theory of hydraulic machines we use the following denotations:
v absolute velocity;
w relative velocity;
u peripheral velocity.
The equation (3.45) written for two particles on the same streamline is:
![]() (3.46)
(3.46)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1713
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved