STRUCTURAL MECHANICS MODULE

STRUCTURAL MECHANICS

MODULE

LABORATORY REPORT

Introduction

Aim & Objective

The main objective is to measure Youngs modulus for the steel and wooden beam using symmetrical loading arrangement. Measurement of the radius of curvature between the supports allows Youngs modulus to be determined. The aim is to obtain values from a single point method, and a graphical gradient method which are to be compared.

Theory

The bending moment, M, about the centre point (taking clockwise as +ve) is:

M = Fa where F= mg

When applying the force with weights of mass m, the force is of course F=mg, where g is acceleration due to gravity = 9.81 m/s².  Therefore it is easy to show that the bending moment is constant at any point between the supports.

The general beam bending equation which relates radius of curvature to bending moment is

Where E is the Youngs modulus, M is the bending moment, R is the radius of curvature and I is the second moment if area.

The second moment of area of a beam of width b, and depth d is given by where d is measure in the direction of bending. The second moment of area is:

The deflection at the centre of the bam can determine the radius of curvature.

Intersecting Chords Theorem:

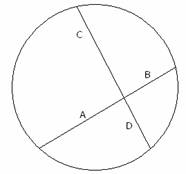A circle that has two intersecting chords, and lengths a,b,c and d as shown, we have a x b = c x d

Using measurements of displacement at the centre, we have:

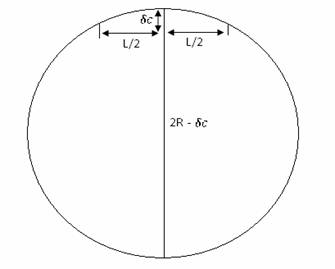
Assuming that we can neglect, giving:

If we substitute equations 1, 3 and 4 into equation 2 we get:

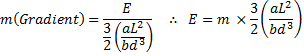
And therefore E can be calculated from the gradient method:

• Measure width b, and the depth, d at six points along the section. Use the average value of each to calculate the second moment of area, I, using Eqn. 3.
• Mount the beam on the supports, ensuring that the grooves for the weight hangers are exactly symmetrical. Position the dial gauge exactly in the centre. Measure lengths L, and a, as shown on the diagram.
• Measure deflection at point C by using a vertically mounted dial gauge as masses of 0.1kg are loaded symmetrically to the weight hangers. Continue this process until the mass on each hanger is 0.5kg.
• Then one at a time, remove the weights symmetrically and record the deflections as they are removed. Use the average of the loading and unloading as your value for
• Perform the calculations using the single point method and the gradient method.

Steel beam

Width b Depth d

L = 0.5 [m] a = 0.338 [m]

Putting weights

Removing weights

Average of the loading and unloading displacements

c = 101 x10^-5 [m]

Single point calculations

Highest applied force

Find radius of curvature

R =

R m

Bending Moment

M =

M = 0.5x9.81x N-m

Young Modulus

E = E =

E = = 204 GPa

Lowest applied force

Radius of curvature

R =

R m

Bending Moment

M =

M = 0.1x9.81x N-m

Young Modulus

E =

E = 206 GPa

Gradient method

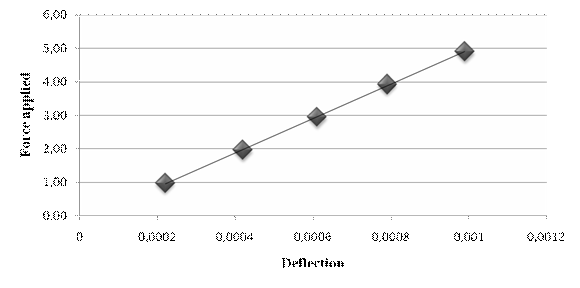
Plot the graph force against deflection

Find Bending Moment

M= (3/2) ((a*L^2)/ (b*d^3))

Where,

a=0.3375

L=0.5

b=

d=0.0052

M= N-m

Find Gradient

G= (change in y-coordinate)/(change in x-coordinate)

G₁= G₂= G_average=

Find Young Modulus

E=G*M/10⁹ GPa

Wooden beam

Width b Depth d

L = 0.5 [m] a = 0.338 [m]

Putting weights

Removing weights

Average of the loading and unloading displacements

c = 101 x10^-5 [m]

Single point calculations

Highest applied force

Find radius of curvature

R =

R m

Bending Moment

M =

M = 0.5x9.81x0.338 = 1.658 N-m

Young Modulus

E = E =

E = = GPa

Lowest applied force

Radius of curvature

R =

R m

Bending Moment

M =

M = 0.1x9.81x N-m

Young Modulus

E =

E = GPa

Gradient Method

Plot the graph force against deflection

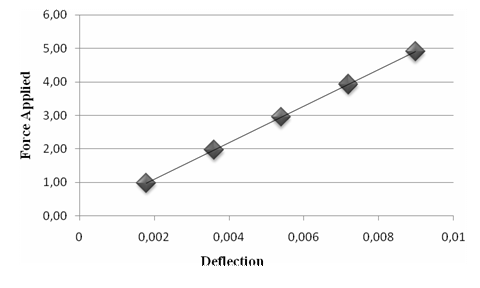
Find Bending Moment

M= (3/2) ((a*L^2)/ (b*d^3))

a=0.3375

L=0.5

b=0.0252

d=0.0055

M=30186755.39 N-m

Find Gradient

G= (change in y-coordinate)/(change in x-coordinate)

G₁=545.758 G₂=545 G_average=545.379

Find Young Modulus

E=G*M/10⁹=16.79 GPa

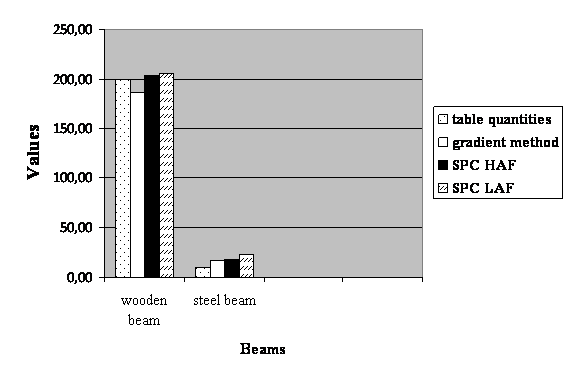
Results

Conclusion

After finishing a laboratory session calculations, it was compared with table quantities and analyzed which method is most precise and accurate.

Looking at the graph was observed that gradient method is more precise for wooden beam, then single point method, but if we look at steel beam result it is obvious that single point method is more correct then the first one.

However especially for me gradient method was easier, because it didnt need to much calculations and formulas. As single point method is more complicated I did twice calculations with incorrect answers, thats why I would prefer gradient method instead single point method.