| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
I. INTRODUCTION
Context
The CrioLapSim program is a research project that has as target the computer aided treatment of tumor through cryosurgery. It was specially tailored for renal tumor detection, but it can be successfully used for other tumor types as well. It gives to the physician the necessary overview of the internal anatomic structure which helps him in studying the desired organs and prepares him for the surgery that follows. More formally speaking, all this research work is materialized in a stereotactic planner and diagnosis tool named DicomTools.
Why is such a program necessary? First of all, it will be much easier for the physician to identify a tumor located inside a patient reconstructed 3D volume instead of identifying it on partial images. The DICOM (Digital Imaging and Communications in Medicine) image files that are processed by the DicomTools application represent the radiography result of the human body and are in fact some image slices that do not provide an overview for the abdominal cavity nor for the tumor volume.
In order to be used, the DICOM image files are read, grouped, sorted and then they are processed using several image processing algorithms and visualization techniques. The application uses the free source libraries VTK (Visualization Toolkit), an ITK (Insight Registration and Segmentation Toolkit). This operation of files processing gives some volume elements which can be viewed in different modes: a real 3D volume of the whole volume or for a region of interest, targeting, segmented or one can choose to go back to previous view, where the slices were not processed.
The targeting view is used in order to identify the tumor. The physician gets an overview image and he can easily see the difference of volume, shape, texture between the kidneys, such that he can identify if the tumor is presented in one of them. Once the tumor is getting localized, he can select the region of interest that comprises the lesion, the rest of the volume being ignored. This delimited region of interest will become the start point for the next operations needed before the physician performs cryosurgery.
The current phase of the research is represented by the process of simulation of cryosurgery through cryogenic models. I have been working to get this process close to the reality by following the specification of the project, the needs of the urologic physician and after a detailed discussion with coordinator of the research project. By the time I write this thesis, the 3D cryosurgery simulation consists of placement of some cryogenic spheres inside the tumor such that the whole volume of the affected kidney is covered. It is desired to replace of cryogenic spheres with another model (ice-ball) close to reality but we are still working on it. A next phase consists of a 3D simulation of the process of freezing and worming that are part of the cryosurgery process and an optimal detection of the points where the cryoprobe will be inserted in the kidney. The present theses only try to theoretically describe the cryosurgery process.
This
research project is developed in collaboration with the Urologic Clinical
Institute and Renal Transplant, Department Urology of Iuliu Hatieganu
The chief coordinator of the research team was Prof. Dr. Ing. SERGIU NEDEVSKI, dean of Faculty of Automatics and Computer Science, the coordinator of the software development team being Matis Istvan.
What is cryosurgery?
Cryotherapy, also called cryoablation and cryosurgery, refers to the use of very cold temperatures to treat disease and is a mainstay therapy for a wide variety of conditions. It is a well-established technology for the treatment of many benign and malignant tumors and lesions, and is also one of the oldest documented forms of medical treatmentthe Egyptians used cold to treat inflammation and injuries as early as 2500BC.
How does cryosurgery work?
To freeze the cancer, special thin probes called cryoablation needles are placed into the tumor. Argon gas is delivered under pressure into a small chamber inside the tip of the needle where it expands and cools, reaching a temperature well below -100s Celsius. This produces an iceball of predictable size and shape around the needle. This iceball engulfs the tumor, killing the cancerous cells as well as a small margin of surrounding tissue while sparing healthy kidney structures. A double freeze-thaw cycle is favored, since studies suggest that consistently larger areas of cell death are achieved with a double rather than single freeze-thaw cycle. Ultra-thin thermal sensors may also be placed at the margin of the tumor to monitor tissue temperature and help ensure that the entire tumor is destroyed.
Cryosurgery approaches
Renal cancer ablation using cryotherapy can be performed through several flexible approaches, so treatment can be customized by the physician to accommodate the patients general health as well as the size and location of the tumor.
Renal cryosurgery can be performed during traditional open surgery, although this approach is rarely used today by experienced kidney surgeons performing kidney cryoablation. Open surgery is more painful, has a longer recovery time and generally results in more complications than minimally invasive surgery. If an open procedure is chosen, it is always performed under general anesthesia and it is recommended that intraoperative ultrasound be utilized as guidance for cryoablation needle placement and positioning.
Laparoscopic-guided cryosurgery on the kidney is a 1 to 3 hour procedure and is almost always performed under general anesthesia. Making 3-4 small incisions, standard laparoscopic technique is used to visualize the kidney, and a laparoscopic ultrasound probe is used to monitor the percutaneous placement of the cryoablation needle(s) and thermal sensors into the tumor. Additionally, the ultrasound probe is used to monitor the tumor and iceball during the double freeze-thaw process, ensuring destruction of the entire tumor as well as the desired margin of surrounding tissue.
Another minimally invasive approach is percutaneous ablation. With percutaneous access, no incisions are made. The patient is positioned in the CT or MRI scanner. The cryoablation needles and thermal sensors are inserted through the skin and positioned in the tumor under the guidance of CT, MRI or Ultrasound and the entire procedure is monitored using CT or MRI. Image-guided percutaneous cryoablation is usually performed under general anesthesia, but can be done under light sedation. Percutaneous cryoablation is the least invasive intervention that can be performed for kidney cancer.
In what situations can cryosurgery be used to treat kidney cancer?
Cryotherapy is indicated as a treatment for cortical or peripheral lesions, for solid lesions less than 4cm, and for patients with a single kidney or poor kidney function. Cryosurgery may also be an option for treating cancers that are inoperable or dont respond to standard treatments. It can also be used for patients who are not good candidates for conventional surgery
Kidney cancer ablation eradicates the cancerous tissue by freezing it. Very precise targeting and control of the energy allows for efficient destruction of tumor cells while leaving healthy kidney tissue intact and functional.
What are the advantages of cryosurgery?
The benefits of renal cancer ablation via cryotherapy are many. Recovery from minimally invasive surgery is often much easier for the patient. The procedure itself is shorter and therefore complications are reduced, including a lower risk of bleeding. Healthy kidney tissue is not disturbed, allowing for maximum retention of kidney function. Multiple small tumors can be treated in one cryosurgical treatment. Image guidance and real-time temperature monitoring usually allow for complete tumor ablation in a single session, but the procedure can be repeated with minimal trauma to the patient if residual tumor is found.
Minimally Invasive Procedure
An advantage of kidney cryoablation is that cryosurgery (freezing) can be performed laparoscopically (with small incisions) or percutaneously (directly through the skin), thus making it a minimally invasive procedure for the treatment of kidney cancer. The minimally invasive nature of the procedure means that it can be performed with minimal blood loss and without a large incision. After surgery, a minimally invasive approach translates into significantly less pain, a shorter hospital stay, and more rapid recovery when compared with open surgery.
Being minimally invasive, cryoablation allows kidney cancer to be treated with much less disruption of patients lives. Patients usually are able to return to family, work, and routine activity in less than half the time that it takes to recover from open surgery.
Shorter Procedure with Fewer Complications
Patients who undergo ablation have less risk of some complications, such as bleeding. Clearly, any time the kidney undergoes surgery, there is a chance of excessive bleeding. However, the risk of excessive bleeding is decreased by not having to cut into the kidney as is typically done with partial or radical nephrectomy. Similarly, not cutting into the kidney minimizes the risk of disrupting the kidneys collection system (the plumbing within the kidney which transports urine), which is a complication known as urine leak.
Should general anesthesia be necessary for the cryosurgical ablation, a shorter procedure also means less time under its effects. This lessens the chance of the patient suffering from any of the complications related to undergoing general anesthesia.
Preservation of
Kidney cancer treatment that allows for the maintenance of adequate renal function is of the utmost importance to the patients ongoing quality of life. Because only the cancer is destroyed during cryoablation therapy and normal kidney tissue is spared, remaining renal function is maximized. This means that the kidneys can continue to perform their many jobs more efficiently than if the entire kidney, or a significant part of it, had been removed.
In addition, sparing a portion of the affected kidney creates more options if a new tumor develops in the patient's second kidney, a risk confronting a small number of people with kidney cancer.
Cryoablation is Repeatable
In most cases, image-guided targeted ablation and real time temperature monitoring assure that only one session of cryotherapy ablation is necessary. Should the patients cancer recur, or if residual tumor is found on follow-up visits, renal cryosurgery can be repeated at the physicians discretion with minimal trauma to the patient.
The role of image processing in the process of Cryosurgery
The Image Processing could be an important component part of cryosurgery process. The first step in this process would be the establishment if the patient can be a candidate for this kind of intervention. Usually, the persons whose tumor doesnt exceed 3 cm in diameter are those for whom the cryosurgery has the most chances of success.
A correct diagnosis is essential before correct treatment can be recommended. It is important for the patient to be examined by a knowledgeable physician. Before the operation of cryosurgery the physician will perform a series of tests for the targeted patient and MRI and CT scans are taken. Once the CT image files are obtained, they can be processed in order to help the physician in his work.
The process of CT image processing has many stages:
The program should load and process image files each containing an image slice.
Before any operation, an efficient management if the DICOM files is imposed. DICOM stands for Digital Imaging and Communications in Medicine and it is the standard file format for storing medical images. So, they should be grouped in consistent sets which permit to create consistent volumes. In order to accomplish this, operations like grouping, sorting, and duplicates removal are needed. One can group the files together in such a way the files from the same patient, same modality, same study and same image acquisition series number to be together. After files have been grouped they are sorted after the position they would take in the image volume if it would be created. Finally duplicate files should be removed to prevent the malformation of the image volume, for example by reading a file twice. A folder loaded with the program may contain mixed image files from many patients and of different modalities (MR, CT) and with different orientations and the application should group these files together, based on the data in the DICOM headers, to form consistent volumes.
The application does basic filtering and processing of the loaded images, like grey level histograms; zoom in and out, contrast and brightness.
The application is capable of exporting images in other formats then Dicom, like jpg, bmp.
The images header information can be visualized by the user too.
After the desired set of image files was loaded, one can reconstruct the volume from those images and apply different processing operation upon it. The reconstruction is done by superposition of the CT image slices in a normal order, to create a natural anatomic volume.
It is possible to select a local volume of interest within the whole reconstructed volume, such that it will delimitate certain organ or a certain part of an organ with the precise scope of isolating it from the rest of the volume.
In this way, the processing operations can be performed on both the whole volume and the isolated region, such that we can concentrate the results over the region of interest.
Operation of scaling, translation and rotation can be performed over the reconstructed volume.
The physician can also select from the whole 3D volume a volume of interest containing the tumor affected kidney. This volume can be zoomed in or out in order to have a better view of the interest area.
The obtained volume will be a start point for creating a model used in the computer aided simulation of the cryosurgery.
A special attention is given to the tumor inside the kidney. The tumor is now represented in an efficient, clear manner, distinct to the rest of the tissue. After the point of interest have been chosen, one can determine the structure it belongs to and the neighborhood regions through segmentation. The segmentation is the method to delimitate a region inside an image through the process of merging pixels, based on different criteria. Having the region of interest delimited and segmented, one can act to reconstruct the volume.
A challenge for our development team is to construct the model only for the tumor volume, not for the whole kidney. In this way, there is a research team who tries to find an efficient method for tumor segmentation. In the same direction, Ive done some considerable efforts to find methods and apply them in the developed application but the results were not the best ones see later. As soon as the results will be close to reality, that is the tumor reconstructed model will correspond to the real tumor volume, it follows a phase where we will numeric evaluate the volume, dimension, some form factors ant the areas of the selected internal sections.
The next step will be the cryosurgery simulation. The purpose of the physician is to cover the whole volume of tumor with cryogenic iceballs as less as possible. For the moment, this iceballs are represented by sphere objects, but we are working to get some models close to those used in the process of cryosurgery, following an integration of those models in the application.
Domain of interest of the project
For implementing the entire requirements, besides medical and biological knowledge one must also have 3D mathematics, visualization and image processing background.
This project brings together both medical and image processing knowledge.
The medical and biological knowledge are necessary in order to understand the complex process of cryosurgery and other kidney operations.
The image processing knowledge is necessary for the segmentation algorithm implementation and for volume reconstruction from CT images.
The visualization knowledge is necessary in order to manipulate the reconstructed volume .
In order to design such a large and complex medical visualization application as DicomTools, to get a robust implementation which offers support for extension and modification, there were used a couple of best practices and design patterns from the object oriented programming domain.
The Digital Imaging and
Communications in Medicine (DICOM) is created by the
The purpose of the DICOM standard is to be a:
hardware interface
a minimum set of software commands
consistent set of data formats
communication of digital image information
development and expansion of picture archiving and communication systems
interface with other systems of hospital information
creation of diagnostic information data bases
[NEMA00]
A DICOM file consists of a set of data elements. Each data element has a tag or id, which consists of the group number and element number of the respective data element. The Value Representation Field (VR) specifies how the data in the value field should be interpreted. In the DICOM standard there are a few well defined value representation types. Some examples are: decimal string (DS), character sequence (CS), unique identifier (UI), etc.
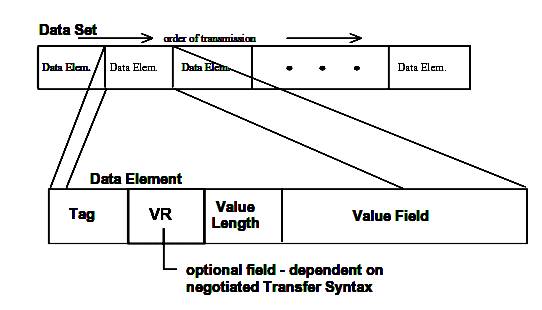
Figure 3.3. DICOM Dataset and Data Element structures.
Data Element Tag: An ordered pair of 16-bit unsigned integers representing the Group Number followed by Element Number.
Note: PS 3.x refers to the DICOM Specification 3, chapter x document downloadable from the internet.
Value Representation: A two-byte character string containing the VR of the Data Element. The VR for a given Data Element Tag shall be as defined by the Data Dictionary as specified in PS 3.6. The two characters VR shall be encoded using characters from the DICOM default character set.
Value Length:
- either a 16 or 32-bit (dependent on VR and whether VR is explicit or implicit) unsigned integer containing the Explicit Length of the Value Field as the number of bytes (even) that make up the Value. It does not include the length of the Data Element Tag, Value Representation, and Value Length Fields
- A 32-bit Length Field set to Undefined Length (FFFFFFFFH). Undefined Lengths may be used for Data Elements having the Value Representation (VR) Sequence of Items (SQ) and Unknown (UN). For Data Elements with Value Representation OW or OB Undefined Length may be used depending on the negotiated Transfer Syntax (see Section 10 and Annex A).
Note: =The decoder of a Data Set
should support both Explicit and Undefined Lengths for VRs of SQ and UN and,
when applicable, for VRs of OW and
Value Field: An even number of bytes containing the Value(s) of the Data Element.
The data type of Value(s) stored in this field is specified by the Data Element's VR. The VR for a given Data Element Tag can be determined using the Data Dictionary in PS 3.6, or using the VR Field if it is contained explicitly within the Data Element. The VR of Standard Data Elements shall agree with those specified in the Data Dictionary.
The Value Multiplicity specifies how many Values with this VR can be placed in the Value Field. If the VM is greater than one, multiple values shall be delimited within the Value Field as defined previously. The VMs of Standard Data Elements are specified in the Data Dictionary in PS 3.6.
Value Fields with Undefined Length are delimited through the use of Sequence Delimitation Items and Item Delimitation Data Elements.
[NEMA00]
The proces of 3D reconstruction from 2D images
The purpose of reading image files is to make available pixels in memory packed into objects which are useful for the programmer and permits further operations. This corresponds to the phase Reconstruct 3D Volume. This reconstruction is taken care of by VTK. VTK reads the pixels of every image file given as input and puts the pixel values into a linear scalar array. Scalars are accessed with logical (extent or i, j, k, integer number) coordinates. Since pixels in an image and voxels in a volume are placed at a certain distance from one another, that is they have a dimension, this information is also stored. In VTK each voxel has also a cell associated with it. The cells are usually rectangular parallelepipeds with their center at the physical (world) coordinates of the voxel values Cx, Cy, Cz and their extremities in the form: (-SpacingX/2 + Cx, +SpacingX/2 + Cx), (-SpacingY/2 + Cy, +SpacingY/2, Cy), (-SpacingZ/2 + Cz, +SpacingZ/2 + Cz). The point at the center has the same scalar value as the voxel value associated with that cell. Scalar values of points in the cell at other positions then the center are computed by interpolation taking into account neighbor cells.
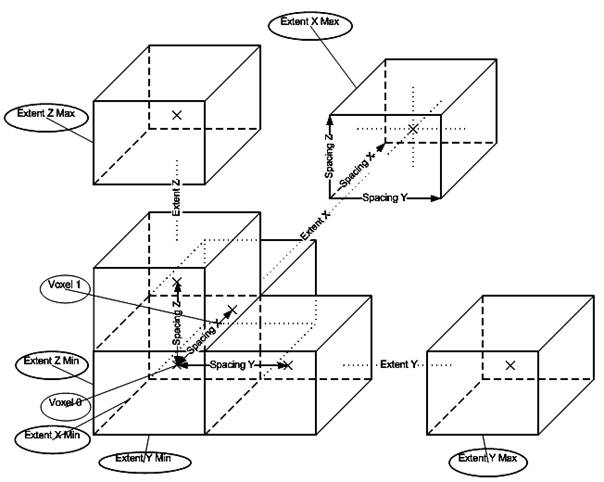
Figure 3.2. Cell structure of the reconstructed 3D volume.
Often image files are oriented in different ways relative to the patient. In order to simplify further computations it is desired to reorient newly constructed image volumes according to a chosen orientation. The destination coordinate system in which all the volumes will be reoriented is the Patient Coordinated System, defined in the DICOM Standard and presented in more details in paragraph 5.3. Implementation Challenges of chapter 5.
After reconstructing and reorienting an image volume it can be used for processing. Such a processing is required when we want to visualize the intersection of the volume with a plane. the class vtkImagePlaneWidget from VTK selects the voxels closest to the intersecting plane and applies texture mapping on the polygon which is the result of the intersection of the image volume with the plane. In order to fill the empty space between voxels interpolation is used. In VTK usually there are tree types of interpolations: nearest neighbor, linear and cubic. After the scalars of the texture are computed they can be mapped to color or intensity values.
Visualization methods help the user to locate a point in the 3D volume. This process is called Targeting. Usually such points of interest, also called targets, will be the destination point where a certain electrode must reach.
When a target is set, the structure in which lies and structures in the vicinity must be reconstructed. This is done by processing the image by applying different filters on it. One of the main goals is to delimit the structure of interest in which the target can be found. This is realized with segmentation. Details about segmentation methods will be presented in paragraph 6 of this chapter: Image Processing.
After the structure of interest is delimited its surface can be reconstructed. This is done with the algorithm Marching Cubes. This is one of the latest algorithms of surface construction used for viewing 3D data. In 1987 Lorensen and Cline (GE) described the marching cubes algorithm. This algorithm produces a triangle mesh by computing isosurfaces from discrete data. By connecting the patches from all cubes on the isosurface boundary, we get a surface representation
The resulting mesh model is further processed in order to reduce its size. Reducing the size of a polygon mesh is done with a decimation algorithm. Triangle mesh decimation is an algorithm to reduce the number of triangles in a triangle mesh. The objective of mesh decimation is to reduce the memory size needed for the representation of an object with good approximation of the original object. This reduction, as the name suggests, can be from 10 to 50 times or even more. This yields not only less memory usage for the representation of the mesh but also faster processing.
The algorithm proceeds as follows. Each vertex in the triangle list is evaluated for local planarity (i.e., the triangles using the vertex are gathered and compared to an 'average' plane). If the region is locally planar, that is if the target vertex is within a certain distance of the average plane (i.e., the error), and there are no edges radiating from the vertex that have a dihedral angle greater than a user-specified edge angle (i.e., feature angle), and topology is not altered, then that vertex is deleted. The resulting hole is then patched by re-triangulation. The process continues over the entire vertex list (this constitutes an iteration). Iterations proceed until a target reduction is reached or a maximum iteration count is exceeded. [VTK04]
Other filters operating on polygonal data are also used to increase the quality of the decimated mesh model, for example smoothing.
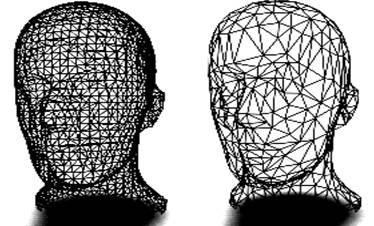
Figure 3.18. Mesh model before (left) and after decimation (right). [SMS02]
Finally the delimited structure of interest can be visualized or the algotithms presented above can be repetead in order to enhance position of the target and the precision of the detected structures.
When mesh-models are initially created, they are usually formed around a specific location (typically the origin) and they usually have a particular size and orientation. This occurs because we are using simplified algorithms which make calculations and understanding easier. However, for the final scene, the models need to be moved, scaled and rotated into their final positions.
These changes can be achieved by applying an affine transformation matrix to the vertices of the polygon mesh. These transformations are implemented by multiplying the appropriate vertex by a matrix.
Often in the application there were several places where we needed to transform a point or a vector from one coordinate system to another.
For example the space of voxels with its coordinate system having the origin in one corner of the parallelepiped representing the voxels and with the axes of the coordinate system being the edges of this parallelepiped starting from the origin is a good coordinate system for image processing algorithms that operate on the entire medical volume.
On the other hand some abdominal structures are reported to have a certain location and orientation relative to other structures. For the doctor is easier to work in a relative coordinate system inside the patients brain.
Therefore coordinate transformations from one coordinate system into another is a very common task in DicomTools.
Below are presented some of the basic transformations in space.
To scale a mesh (stretch along x-axis) we apply the following to each point:
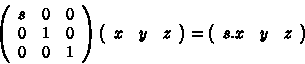
In this case, x component of each point has been multiplied by s.
This scaling matrix can be generalized as
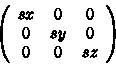
where sx, sy and sz are scaling factors along the x-axis, y-axis and z-axis respectively.
To rotate a
point ![]() degrees
about the z-axis, we multiply the point by the following matrix:
degrees
about the z-axis, we multiply the point by the following matrix:
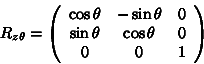
For rotations about the x-axis and y-axis, we apply the following:
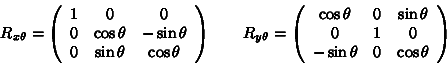
In order to translate a point we can add a vector to it:
![]()
Scaling and rotation are performed
by matrix multiplication, and translation is performed by vector addition. It
would be simplify matters if we could also apply translation by matrix
multiplication. Vector addition can be simulated by multiplication by using
Homogeneous co-ordinates. To convert a vertex to Homogeneous
co-ordinates, we simply add a ![]() co-ordinate,
with a value one:
co-ordinate,
with a value one:
![]()
To convert a matrix to homogeneous co-ordinates we add an extra row and an extra column:
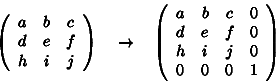
Using the homogeneous matrix, translation can be implemented by matrix multiplication:
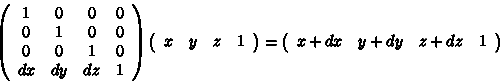
[Power04]
3D visualisation techniques
The marching squares algorithm aims at drawing lines between interpolated values along the edges of a square, considering given weights of the corners and a reference value. Let's consider a 2D grid as shown in the next picture.
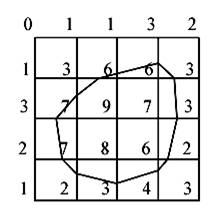
Figure 3.10. The marching square algorithm example.
Each point of this grid has a
weight and here the reference value is known as 5. To draw the curve whose
value is constant and equals the reference one, different kinds of
interpolation can be used. The most used is the linear interpolation.
In order to display this curve, different methods can be used. One of them
consists in considering individually each square of the grid. This is the
marching square method. For this method 16 configurations have been enumerated,
which allows the representation of all kinds of lines in 2D space.
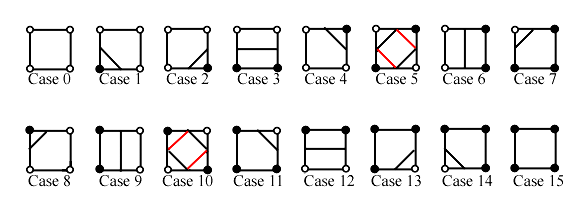
Figure 3.11. The marching squares algorithm cases.
While trying this algorithm on different configurations we realize that some cases may be ambiguous. That is the situation for the squares 5 and 10.
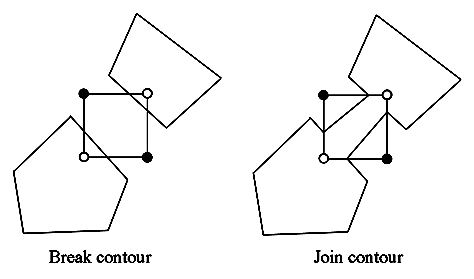
Figure 3.12. The marching squares ambiguous cases.
As you can see on the previous picture we are not able to take a decision on the interpretation of this kind of situation. However, these exceptions do not imply any real error because the edges keep closed.
Following the marching squares algorithm we can adapt our approach to the 3D case: this is the marching cubes algorithm. In a 3D space we enumerate 256 different situations for the marching cubes representation. All these cases can be generalized in 15 families by rotations and symmetries:
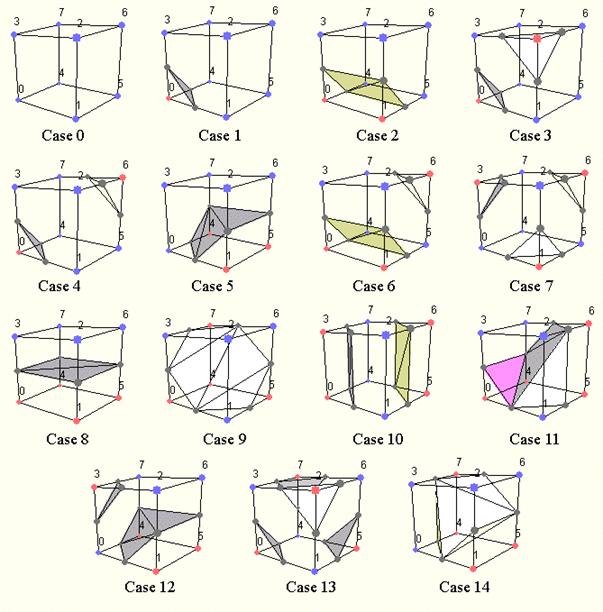
Figure 3.13. The cases of the marching cubes algorithm.
In order to be able to determine each real case, a notation has been adopted. It aims at referring each case by an index created from a binary interpretation of the corner weights.
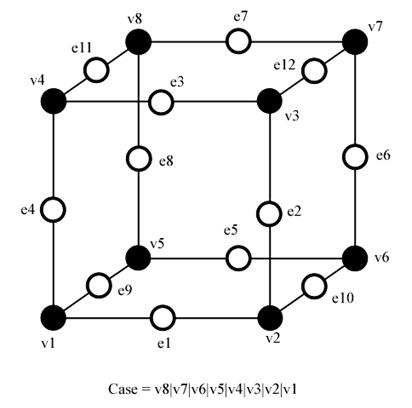
Figure 3.14. Notation of the marching cubes cases.
In this way, vertices from 1 to 8 are weighted from 1 to 128 (v1 = 1, v2 = 2, v3 = 4, etc.); for example, the family case 3 example you can see in the picture above, corresponds to the number 5 (v1 and v3 are positive, 1 + 4 = 5).
To all this cubes we can attribute a complementary one. Building a complementary cube consists in reversing normals of the original cube. In the next picture you can see some instances of cubes with their normals.
In order to realize the visualization of a structure from a 3D volume or of the volume itself several image processing algorithms were used.
For equalizing the histogram of a volume the algorithm Histogram Equalization by Pair wise Clustering was used. It uses a local error optimization strategy to generate near optimal quantization levels. The algorithm is simple to implement and produces results that are superior then those of other popular image quantization algorithms. [Velho]
This algorithm was adapted to grey scale images.
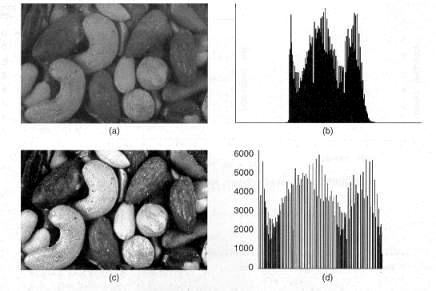
Figure 3.28. (a) Original image; (b) Histogram of original image; (c) Equalized image; (d) Histogram of equalized image. [Luong]
In many cases it is much better to preprocess or post process an image with a certain filter, because this way the quality of the image can be increased. Some of these filters include noise removal filters, like the edge preserving Gaussian Smooth filter, filters used on binary images like eroding and closing. For more details see [Fisher94].
Image segmentation
IMAGE SEGMENTATION is one of the most important issues in computer aided medical imaging. It is used in the analysis and diagnosis of numerous applications such as the study of anatomical structure, localization of pathology, treatment planning, and computer-integrated surgery [1]. There are two main reasons for the use of computer aided segmentation: one is to improve upon the conventional user-guided segmentation [2], and the other one is to acquire segmentation prior to visualization or quantification for the analysis of medical images [3]. In recent years, many computer-aided diagnostic systems have been developed to assist in the making of precise and objective diagnoses for lung cancer, liver tumor, and breast diseases. </ >
<FULLTEXT1>
Segmentation techniques can be divided into classes in many ways [3,4], according to different classification schemes. However after a literature survey, we divide the existing kidney segmentation and analysis methods into two main groups:
1) model-based techniques;
2) region-based techniques.
Model-based procedures include snake algorithms (deformable model, active contours etc.), as initially proposed by Kass et al. [5], and level set methods (aswell as fast marching methods), proposed by Osher and Sethian [6]. These techniques are based on deforming an initial contour or surface towards the boundary of the object to be detected. The deformation is obtained by minimizing a customized energy function such that its local minima are reached at the boundary of the desired structure. These algorithms are generally fast and efficient but the outcomes are often low in accuracy for the following reasons. Since the stopping term of the deformation evolution depends on the image gradient flow being approximately zero, this often forces the contours to stop several voxels away from the desired boundary.Thus the active contour sometimes does not match the boundary of the structure accurately, especially in regions with steep curvature and low gradient values.
Since a surface tension component is incorporated into the energy function to smooth the
contour, it also prevents the contour fully propagating into corners or narrow regions. Increasing the number of the sample nodes along the contour can improve the situation, but at a significant increase in computational cost. The existence of multiple minima and the selection of the elasticity parameters can affect the accuracy of the outcome significantly.
Region-based algorithms include region growing [7],morphological reconstruction [8] and watershed [9]. Since these procedures are generally based on neighborhood operations, and examine each pixel during the evolution of the edge, the outcomes are usually highly accurate. On the other hand, although there are several optimized algorithms in the literature [10 ], they are generally computationally intensive.
</FULLTEXT1>
< >
Segmentation approaches survey
Pohle and Toennies developed a region-growing algorithm that learns its homogeneity criterion automatically from characteristics of the region to be segmented [3], [8], [9]. This approach is less sensitive to the seed point location. Kim et al. and Yoo et al. proposed similar approaches for kidney segmentation based on the pixel value distribution of the organ and the mesh operation [10], [11]. Kobashi and Shapiro described a knowledge-based procedure for identifying and extracting organs from normal CT imagery [12]. The detection result was
rated 85% grade A from testing of 75
images from three patients. Mavromatis et al. performed medical image
segmentation through tissue texture analysis and distribution of directional
maximums [13]. Wang et al. proposed a constrained optimization approach
in which deformable contour can be computed as extra constraints within the
contour energy minimization framework [14]. Tsagaan and
approach for automatic kidney segmentation [15], [16]. They used a deformable model represented by the grey level appearance of kidney and its statistical information of the shape. They tested 33 abdominal CT images. The degree of correspondence between automatic segmentation and manual positioning was 86.9%.
Automatic kidney segmentation
Introduction
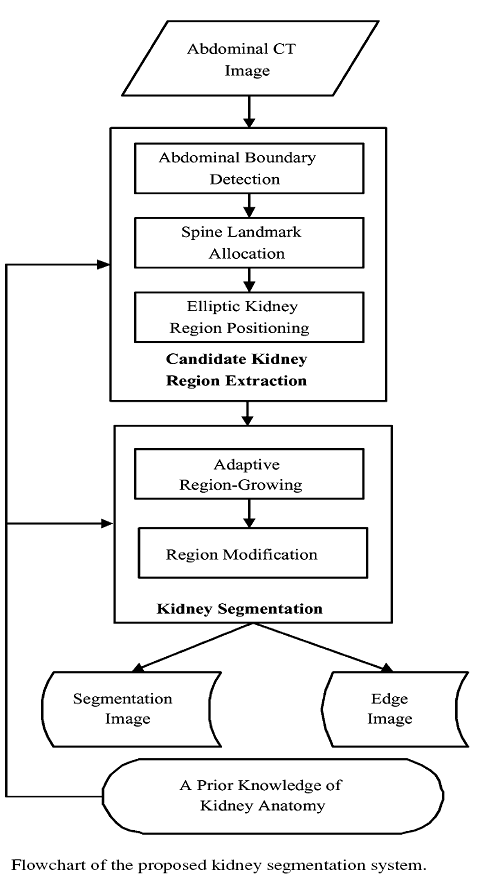
An efficient method combining the consideration of anatomic structure with a series of image processing techniques has been proposed for kidney segmentation of abdominal CT images.The kidney region is first obtained based on geometrical location, statistical information, and a priori anatomical knowledge of the kidney. This approach is applicable to images of different sizes by applying relative distance of the kidney region to the spine. Furthermore, it was proposed an elliptic candidate kidney region extraction approach with progressive positioning for the center of ellipse on the consecutive CT images.
Daw-Tung Lin, Member, IEEE, Chung-Chih Lei, and Siu-Wan Hung proposed a method that was to combine the advantages of the region-based and model-based methods and develop anautomatic system for kidney segmentation on a parallel series of abdominal CT images. A wide variety of prior knowledge regarding anatomy and image processing techniques has been incorporated. The major features of the proposed system are
the location of the spine is used as the landmark for the coordinate references,
2) an elliptic candidate kidney region extraction with progressive positioning of the center of ellipse on the consecutive CT images,
3) novel directional model for a more reliable kidney region seed point identification, and
4) adaptive region growing controlled by the properties of image homogeneity.
The flowchart of the proposed automatic kidney segmentation system is illustrated in Fig. 1.
Extraction of the candidate kidney region
A typical abdominal CT image is very complicated. It may contain kidney, liver, spleen, spine, fat, and pathologies. To achieve the goal of automatic kidney segmentation, they proposed a coarse to fine approach. The abdominal cavity is first delineated by an abdomen contour detection algorithm. Based on this contour, the spine can be marked as reference, and the candidate kidney regions (Rk identified accordingly. Since the slice thickness for CT scanning and machine settings might differ from hospital to hospital and from patient to patient, we execute the extraction process starting from the mth slice (m n/ ). This is approximately the middle slice of the sequence in which the kidney is usually obvious and easy to review, and where n denotes the total number of slices in one set. The abdominal cavity boundary is usually a bright line formed by the X-ray reflection from skin. The outer-boundary area on CT image is usually a dark area. Thus, the outer-boundary area is determined by justifying whether there are dark pixels on the opposite sides in two directions: seven pixels vertically or three pixels horizontally. This procedure will ensure that all thin line segments and the non-black blocks will be removed outside the abdomen. It is possible to discard small threads inside the boundary. However, the main purpose is to delineate the boundary, the inside area will be retained for the next stage. The boundary detection algorithm is shown as follows.

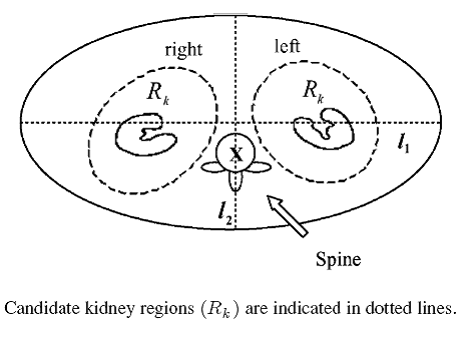
The spine is an important landmark, and is used to determine the position of kidney. Once the abdominal boundary has been determined, we let l1 be the length of horizontal axis and l2 be the length of vertical axis. The spine, denoted as X in Fig. 2, is located at position (0 l l2). The candidate kidney region (Rk is then obtained by rotating a designed ellipse with a short axis length of 0 l1 and long axis length of 0 l2. The center (x , y0) of the initial ellipse is located at a distance of (0 l1) to the spine. Generally, both kidneys appear in an angle of inclination in the range of 40
Kidney segmentation
After the candidate kidney region has been extracted, it follows to retrieve the kidney from the Rk In order to do that a series of image processing techniques including region growing, labeling, filling, as well as mathematical morphology were used.
Adaptive Region Growing

There are three issues that need to be addressed in the region growing process: initial seed selection, the similarity criterion of growing, and the formulation of termination criterion. To resolve these problems, it was proposed an adaptive criteria for region growing by constructing a model of five search directions (see Fig. 4) in terms of location frequency inside the Rk Since the kidney is a homogeneous area, the difference of grey levels between the maximum and minimum pixel values in a 7 x 7 mesh was computed.
If the difference is larger than a threshold 1 (initially set to 20), then the center of mesh resides in a nonhomogeneous area and it is not suitable to be an initial seed of kidney area. Generalization is preserved through the normalization process of 60 training images in which the grey level of the left and right elliptical candidate kidney region images were adjusted to the corresponding mean values (124 and 116).
The asymmetry of mean values is due to the enhancement of contrast medium and the nature of different anatomic structure of the left and right elliptical region. The search procedure is continued until the entire Rk has been tested. In addition, to adapt for slight variations in contrast, we proposed to update the threshold value 1. If no homogeneous mesh is found in any direction, then 1 will be updated (increased by 5). By applying the updated 1, the search process will be performed all over again, until 1 is larger than 50, which means that it is not a normal renal area
Region Modification and Contour Visualization
Once the binary image has been obtained from the adaptive region growing process, trivial and irregular objects may remain and holes may scatter inside the organ. Region modification is essential to improve the segmentation accuracy under various conditions arising from clinical practices such as the timing and rate of contrast media injection, image intensity variations, and blood flow rate.The region modification can be implemented by utilizing a series of image processing skills including: pixel filling, erosion, labeling, and dilation [6].
< >
<FULLTEXT1>
Multistage hybrid segmentation
Proposed Workflow
A flow chart of the algorithm is shown in Fig. 1. In the first stage, a morphological recursive erosion is employed to reduce the connectivity between the object and its neighboring tissues. Then a fast marching method is used in the second stage to greatly accelerate the initial propagation from the user-defined seed structure to the vicinity of the boundary of object. In the third stage, a morphological reconstruction algorithm is used [8] to refine the propagation to achieve a highly accurate boundary. At the end of the segmentation procedure, morphological recursive dilation is implemented, using the same number of iterations as recorded in stage one, to recover regions lost during the initial erosion, but at the same time avoiding re-connection to the surrounding structures. The segmented result may be presented to the user by volume rendering (ray casting) or surface rendering (matching cube) methods.
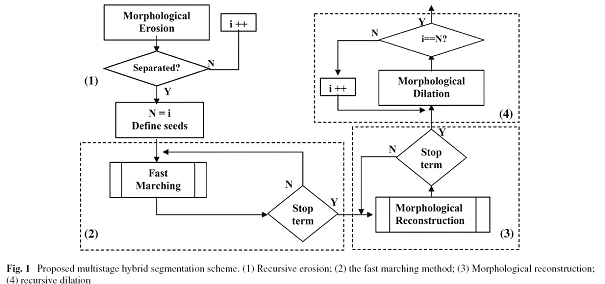
Multistage hybrid segmentation approach
The segmentation algorithm is a multistage procedure, which is composed of four major stages (Fig. 1):
Stage 1 Reduce the connectivity between the object region and the neighboring tissues. Recursively erode the input 3D image using a structuring element base (e.g. a sphere with 1 pixel radius) until the desired object region is completely separated from the neighboring tissues, as determined by the operator. Record the iteration number N for later use in stage 3. This step is designed to prevent overflow during the propagation in stages 2 and 3.
Stage 2 Perform initial evolution of the front.The fast marching method is employed here to initially propagate the userdefined seed to a position close to the boundary.
Stage 3 Refine the contours created in stage 2. Since the speed function in the fast matching method falls to zero sharply, the front could stop a few voxels away from the real boundary. Here, a grayscale morphological reconstruction algorithm is employed to refine the front as a final check. The output from stage 2 is employed as marker, while the original image is used for the mask.
Stage 4 Recover the lost data elements from stage 1. During the recursive erosion in stage 1, part of the object (usually around the edges) is also often eliminated. To recover these lost components, the recursive dilation method is employed. The reconstructed object surface is dilated recursively using the same number of iterations N as recorded in stage 1, which results in the recovery of the object surface to the original position.We note that the resultant image will not in general exactly correspond to the original image, but be smoothed, since erosion, followed by dilation corresponds to an opening operation. It nevertheless removesmost of the noise surrounding the desired boundary. However, if we use a sphere with 1 pixel radius as the structuring element, and employ a small number of iterations to reduce the connectivity, the surfaces of smooth convex structures may be recovered accurately.
</FULLTEXT1>
iccv-ws2005-segment
Atlas based segmentation
A lot of research has been performed on the segmentation of complex CT/MR images using the atlas-based approach. Most existing methods use 3D atlases which are more complex and difficult to control than 2D atlases. They have been applied mostly for the segmentation of brain images. Segmentation of 3D CT Volume Images Using a
Single 2D Atlas presents a method that can segment multiple slices of an abdominal CT volume using a single 2D atlas. Segmentation of human body images is considerably more difficult and challenging than brain image segmentation.
A lot of research has been performed on the segmentation of CT and MR images. In particular, the atlas-based approach is most suited to segmenting complex medical images because it can make use of spatial and structured knowledge in the segmentation process. Typically, 3D atlases are used to segment the surfaces of the anatomical structures in 3D CT/MR images [17]. However, 3D atlases are more complex and difficult to construct than 2D atlases. There are much more parameters to control in 3D atlases. Thus, 3D atlas-based algorithms tend to be developed for segmenting specific anatomical structures. It is not easy to adapt the algorithms to the segmentation of other anatomical structures by simply changing the atlas.
An alternative is to use multiple 2D atlases to segment a CT/MR volume. In this case, it is necessary to understand how many 2D atlases will be needed to segment all the slices in a volume. The worst case scenario of one atlas per image would defeat the idea of using 2D atlases because the stack of 2D atlases would contain the same amount of complexity as a 3D atlas. It also makes practical application difficult because there are many slices in a typical CT/MR volume.For example, in the case of liver transplant, more than 200 abdominal CT images are taken
Interestingly, most work on atlas-based segmentation has been focused on brain MR images [13, 8, 6] or heart MR images [4, 7]. Less work is done on the segmentation of abdominal CT images [5], which is considerably more difficult and challenging than segmentation of brain images..
Atlas-based segmentation is performed using atlas-based registration technique. The registered atlas contours (2D case) and surfaces (3D case) are taken as theboundaries of the segmented anatomical structures. Fully automatic atlas-based segmentation problems map to atlas-based registration problems with unknown correspondence. Solutions to these problems have to solve both the registration and the correspondence problems at the same time. These problems are therefore much more difficult to solve than semi-automatic registration and segmentation, which require some user inputs such as landmark points [9].
An atlas-based segmentation algorithm typically comprises two complementary stages: (1) global transformation of the atlas to roughly align it to the target image, and (2) local transformation or deformation of the atlas to accurately register it to the corresponding image features. Global transformation often serves to provide a good initialization for local deformation. Without a good initialization, local deformation may deform the atlas out of control and extract wrong object boundaries (see Section 3.3 for an example).
In the global transformation stage, spatial information (i.e., relative positions) of various parts of an atlas is used to determine how the atlas should be transformed. Both similarity [2, 3, 5] and affine [4, 6, 7] transformations have been used. An iterative optimization algorithm is applied to compute the optimal transformation parameters. In each iteration, the possible correspondence between the atlas and the target is usually determined based on the closest point criterion in the same way as the Iterative Closest Point algorithm [10].
In the local deformation stage, several main approaches have been adopted. The method in [11] applies iterative optimization to determine optimal local affine or 2nd-order polynomial transformations that deform the various parts of the atlas to best match the target. The methods in [4, 5] also apply optimization techniques but they represent the 3D atlas surface using B-splines and thin-plate spline constraint. These methods ensure that the extracted surfaces are smooth but they require a large number of parameters to represent complex convoluted surfaces of the brain.
A popular method is to apply the so-called demons algorithm [2, 3, 6, 12]. It regards the atlas and the target as images at consecutive time steps, and applies the optical flow algorithm to determine the correspondence between them. As for any optical flow algorithm, it suffers from the so-called aperture problem and may not be able to handle large displacements between corresponding points. It is also easily affected by noise and extraneous image features.
In addition to applying atlas-based registration technique, [5, 7] included a final classification stage that classifies each pixel to a most likely anatomical category. This stage is required because the registration algorithms are not precise enough in aligning the atlas boundaries to the object boundaries in target images. Classification approach can improve the accuracy of the segmentation
result. However, it may not be able to handle segmentation of regions which are nonuniform in intensity and texture. For example, the air pocket in the stomach appears to have the same intensity as the background (Section 4, Fig. 3a, 5). Classification algorithms will be easily confused by such nonuniform regions.
Automatic Atlas-Based Segmentation
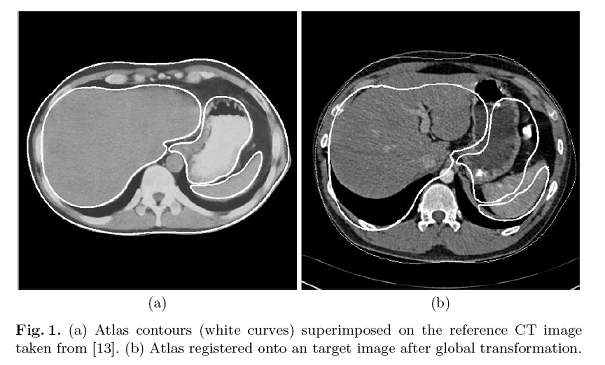
Uses a 2D deformable atlas to segment the major components in abdominal CT images. The atlas consists of a set of closed contours of the entire human body, liver, stomach, and spleen, which are manually segmented from a reference CT image given in [13]. As shown in Fig. 1, the reference image is significantly different from the target image in terms of shapes and intensities of the body parts. Such differences are common in practical applications.
The automatic segmentation algorithm consists of three stages:
Global transformation of the entire atlas.
This stage performs registration of the atlas to the target input image with unknown correspondence. First, the outer body contour of the target image (target contour) is extracted by straightforward contour tracing. Next, the outer body contour of the atlas (reference contour) is registered under affine transformation to the target contour using Iterative Closest Point algorithm [10]. After registration, the correspondence between the reference and target contour points is known. Then, the affine transformation matrix between the reference and target contours is easily computed from the known correspondence by solving a system of over-constrained linear equations. This transformation matrix is then applied to the atlas to map the contours of the inner body parts to the target image. After global transformation, the centers of the reference contours fall within the corresponding body parts in the target image (Fig. 1b). The reference contours need to be refined to move to the correct boundaries of the body parts.
Iterative local transformation of individual parts in the atlas.
This stage iteratively applies local transformations to the individual body parts o bring their reference contours closer to the target contours. The idea is to search the local neighborhoods of reference contour points to find possible corresponding target contour points. To achieve this goal, it is necessary to use features that are invariant to image intensity because the reference and target
images can have different intensities (as shown in Fig. 1).
Atlas contour refinement using active contour algorithm.
The last stage performs refinement of the atlas contour using active contour, i.e., snake algorithm [14] with Gradient Vector Flow (GVF) [15]. The original snake algorithm has the shortcoming of not being able to move into concave parts of the objects to be segmented. This is because there is no image forces outside the concave parts to attract the snake. GVF diffuses the gradient vectors of the edges outward, and uses the gradient vectors as the image forces to attract the snake into concave parts.
Comparisons with Existing Work
Most existing atlas-based approaches adopt a two-stage approach consisting of global transformation followed by local deformation. On the other hand, this method consists of three stages, namely (1) global affine transformation, (2) iterative local affine transformation, and (3) snake deformation. The first two stages are similar to those in [1], but the method in [1] is developed for registering an atlas to a brain surface that is already segmented.
[5] also presented a method for segmenting abdominal CT images. However, their atlas registration algorithm is not accurate enough, and a final classification stage is applied to classify the image pixels into various anatomical categories.
IMPORTANT
Watershed Segmentation
The principle of the watershed technique is to transform the gradient of a gray level image in a topographic surface. Then, let us consider that all minima of the image become sources from which water floods and forms catchment basins immerging the surface. This algorithm stops when two catchment basins from two different sources meet. We then obtain a watershed which is the boundary between the two minima influence zone. For more details, refer to [2].
The main problem of this initial method is that in real images which are often noisy, there are a lot of local minima. This leads to over-segmentation as we can see on Figure 1. Each minimum creates catchments basin represented with a different color. Watersheds can be seen as white lines.

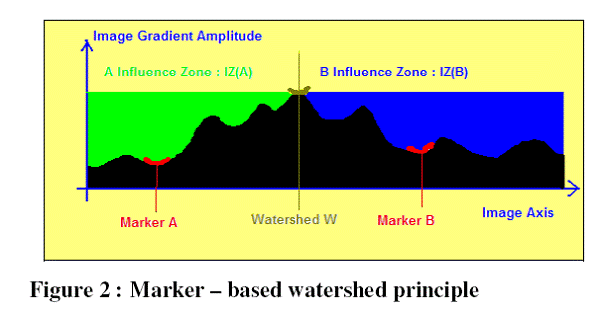
Marker-based Watershed
In order to avoid the over-segmentation problem, aclassical solution is to use markers inside and outside the tumor. Figure 2 shows the principle of marker based watershed segmentation [2]: as for the initial watershed method, the image gradient is considered as a landscape with mountains where there is a high gradient and valleys where it is a low one. An immersion of this landscape with water flooding from two markers (A and B) stops when their influence zone meet: this is the watershed line (W) separating the two areas. The main difference is that the immersion of the gradient surface begins only from selected markers and not from all minima.
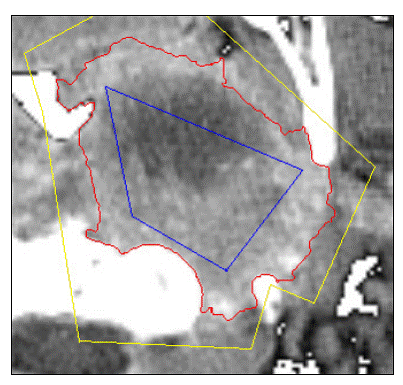
As we can see in Image 1, there are two initial marker sets. The blue one labels the inside part of the tumor, the yellow one, the outside. If we use these markers as initial flooding source we obtain only two catchments basins so two areas delimited by the watershed represented by the red line. Here we can much better use this result to separate the tumor from the rest of the image than by using classical watersheds (Figure 1).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2357
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved