Principiul minimei actiuni in mecanica relativista

Principiul minimei actiuni in mecanica relativista

Principiul minimei actiuni afirma ca prin orice sistem mecanic exista o integrala S numita actiune care este minima (externa) pentru miscarea reala si a carei variatie este, deci, nula. Vom construi actiunea pentru o particula relativista libera (nesupusa unor forte exterioare). Considerand ca actiunea nu trebuie sa depinda de sistemul de referinta si ca sub semnul integrala trebuie sa fie o diferenta de ordinul intai rezulta ca actiunea pentru o particula libera va avea forma:

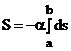unde este o constanta pozitiva semnul minus asigura posibilitatea ca actiunea sa fie minima iar integrala se ia pe linia de univers a particulei intre evenimentele date a si b.

Putem apoi deduce functia Lagrange a particulei relativiste libere:

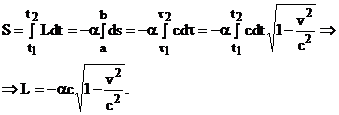
La linia nerelativista dezvoltam L in serie de puteri ale lui si pastram primii termeni :

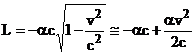
Eliminam constanta - in acord cu proprietatea 3 a functiei Lagrange si egalam cu expresia clasica:

obtinem in final:

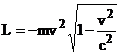si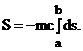

8. Cuadriimpulsul

Impulsul relativist tridimensional se calculeaza conform definitiei:

Componenta k este:

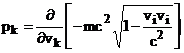unde

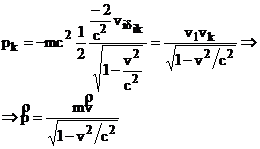
Derivand la timp impulsul 3 - dimensional se obtine forta:

in cazul in care se modifica doar marimea vitezei:

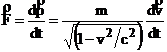
in cazul in care se modifica doar directia vitezei :

In cele doua cazuri raportul dintre forta si acceleratie este diferit. Energia particulei se calculeaza astfel:

.

In cazul particulei libere relativiste expresia de mai sus in coordonate carteziene devine:

Observam ca daca particula este in repaus ea poseda energia de repaus:

- energia cinetica relativista. Daca un pozitron (antiparticula electronului - are aceleasi proprietati, mai putin sarcina care este pozitiva) se intalneste cu un electron la o viteza relativa mica, amandoi dispar intr-un flash radiatie electromagnetica. Se emit cel putin doi fotoni (pentru conservarea impulsului) a caror energie a fost masurata = . Energia de repaus a substantei s-a transformat in energie a radiatiei electromagnetice. Un alt exemplu este oferit de celebra cutie a lui Einstein. Cutia contine un bec la un capat al ei si un perete absorbant la celalalt. Ea este in absenta campurilor gravitationale si a oricaror interactiuni din exterior. Daca becul emite un flash luminos, trenul de unde calatoreste prin cutie si este absorbit la celalalt capat. Teoria electromagnetismului a lui Maxwell va spune ca flash-ul luminos transporta energia E si impulsul E/C. Astfel cand el paraseste becul, cutia sufera un recul pentru conservarea impulsului:

.

Dupa timpul lumina este absorbita in celalalt capat. In acest interval de timp cutia parcurge distanta : . Astfel, desi nu avem forte externe centrul de masa al sistemului s-a miscat. Explicatia consta in faptul ca nu am considerat faptul ca traseul de unde cu energia E poseda si (m) pe lungimea L a tubului astfel incat:

Md = m L,

pentru pastrarea echilibrului. De aici aflam masa transportata de lumina: in acord cu relatia lui Einstain. Fotonii au masa de miscare si impulsul dar nu au masa de repaus , ei fiind tot timpul in miscare cu viteza c fata de orice observator.

O ultima observatie se refera la relatia dintre masa si energie. Astfel sa consideram un atom de hidrogen in repaus. El este alcatuit dintr-un proton si un electron tinuti impreuna de forta electrostatica. Pentru a descompune acest sistem este necesar un foton cu energia de 13,6 eV care ionizeaza atomul, adica separa electronul de proton la o distanta suficient de mare pentru ca atractia lor electrostatica sa inceteze. Masa atomului de hidrogen este cu 13,6 eV/c² mai mica decat suma maselor electronului si protonului izolat.

In cazul nucleelor, fortele dintre nucleoni sunt mult mai puternice. Astfel cand un atom de hidrogen se combina cu unul de litiu pentru a forma doi atomi de heliu defectul de masa este mult mai mare. Energia emisa este de 17 MeV, de cel putin un milion de ori mai mare decat cea emisa in cele mai evidente relatii chimice. La explozia unui milion de tone de TNT modificarea de masa este de cateva sute de grame in timp ce la explozia unei bombe de hidrogen avand aceeasi masa defectul de masa este de aproximativ 50kg.. Putem afirma ca energia unui corp in repaus contine pe de o parte energia de repaus a particulelor componente, energia cinetica a acestora si energia de interactiune.

Impulsul clasic este important deoarece se conserva in sisteme izolate. Vom introduce notiunea de cuadriimpuls si vom cauta invarianti Lorentz care sa implice aceasta marime.

Definim cuadriimpulsul: pentru componentele contravariante si pentru cele covariante. Produsul scalar este:

Componentele sunt:

(componenta temporala) si

.

Deci si modulul patrat va fi: : relatia relativista intre energie si impuls. Expresia este invariantul fundamental al dinamicii teoretice relativitatii restranse (scalar). Transformarea componentelor 4 - impulsului la schimbarea de referential se face in acord cu definitia:

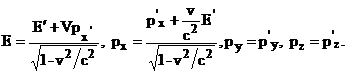
In cazul fotonilor, ecuatiile Planck-Einstein si aplicate relatiei de transformare a energiei conduc la:

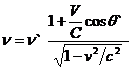
unde este unghiul format in sistemul de referinta in miscare de impulsul fotonului cu axa .

Cand 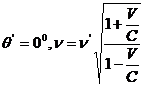(efectul Doppler longitudinal) si cand 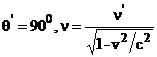(efectul Doppler transversal).

Efectul Doppler a permis prin masurarea deplasarii spre rosu a frecventelor fotonilor proveniti din galaxii indepartate, sa se deduca faptul ca acestea se indeparteaza de noi cu o viteza care creste cu indepartarea si deci, sa se afirme ca ne aflam intr-un univers in expansiune.

Vom arata acum ca 4- impulsul unui sistem izolat se conserva. Principiul minimei actiuni afirma ca pentru miscarea efectiva actiunea este extrema. Matematic acesta se exprima prin:

unde 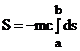este actiunea particulei libere. Exprimand avem:

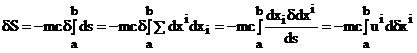
Integrand prin parti:

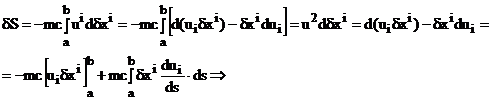
Tinand cont de conditiile la limita (traiectoriile comparate trec prin acelasi punct) obtinem:

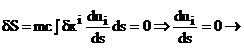cuadriviteza unei particule libere ;i deci ;i 4 - impulsul sunt constante.