Calculul lui Pi

Calculul lui Pi

Prima metoda pe care o putem utiliza pentru a determina o valoare aproximativa a numarului PI , este pornind de la definitia lui : raportul dintre circumferinta unui cerc si diametrul acestuia. Este suficient deci sa luam un obiect de forma circulara ca roata unei biciclete si sa-i masuram diametrul si circumferinta , apoi , prin calculul raportului dintre acestea obtinem numarul Pi.

Alte metode de aproximare a numarului PI

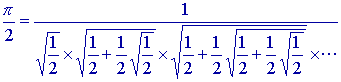foarte rapida: pi=3.141592653288 dupa16 iterari

( Franois Vite 1593

destul de rapida : pi=3.1415797 dupa 16 iterari

( Leonhard Euler )

foarte lenta: pi=3.050 dupa 16 iterari

(John Wallis 1655 )

extrem de lenta : pi=3.079 dupa 16 iterari , si este nevoie de 136.121 iterari pentru a avea 4 si 5 zecimale, si 2.886.751 pentru 6

Metoda lui Arhimede pentru calculul lui Pi

Arhimede(287-212 iHR.) utiliza figuri geometrice regulate inscrise si circumscrise pentru a calcula o aproximare a suprafetei unui cerc.

Este suficient sa se incadreze cercul intre doua poligoane de dimensiuni cunoscute , obtinand o incadrare a ariei discului intre cele doua arii de poligoane .

Exemplu:

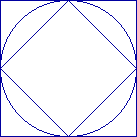
N=4

2² > A > ()²
4 > A > 2 et A = Pi * R = Pi * 1 = Pi
deci Pi = 3 +/-1

Numarul Pi si poezia .

Numarul de litere al fiecarui cuvant din poezia de mai jos reprezinta una din zecimalele lui Pi .

Que j'aime faire apprendre un nombre utile aux sages.

Immortel Archimde, artiste ingnieur,

Qui de ton jugement peut priser la valeur

Pour moi ton problme eut de srieux avantages.






Un poem in limba engleza , de forma circulara in care numarul de litere al fiecarui cuvant reprezinta o zecimala a lui Pi.