| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The equation 2x 3y = 12 is called a linear equation because it is graphed as a straight line in the xy-plane. All variables in a linear equation are of first degree. When we have a finite set of linear equations, we call it a system of linear equations. The main objective of this section is to find solutions to systems of linear equations. We will focus only on a system consisting of two linear equations.
A system of two linear equations in two unknowns, x and y, is usually written in the form
![]() where a, b,
c, d, e, and f are all real numbers.
where a, b,
c, d, e, and f are all real numbers.
An example of a system of two linear equations is
![]()
The solution of a system of linear equations is a set of real numbers that simultaneously satisfies each equation in the system. When the system consists of two equations, the solution is a set of ordered pairs that makes both equations a true statement.
Determine whether (-1, 4) is a solution of the system
![]()
Equation (1) Equation
(2) 3x + 2y =
5 x + 2y
= 7 3(-1) + 2(4) = 5 (-1) + 2(4) = 7 -3 + 8 = 5 -1 + 8 = 7 5
= 5 true 7 = 7 true
Solution:
![]()
Therefore, the ordered pair (-1, 4) satisfies the two linear equations.
Determine whether the ordered pair is a solution of the given system of linear equations.
a) (-3, -5)![]()
b) (1, -2) ![]()
c) (-1, -1) ![]()
Not all systems of equations have common solutions. When a system has at least one solution it is called consistent. When the system is consistent, then there are two possible situations: either the system has a unique solution or it has an infinitely many solutions. If the system has a unique solution, the equations are called independent. If the system has infinitely many solutions, the equations are called dependent.
![]()
![]()
![]()
![]()
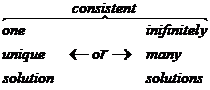
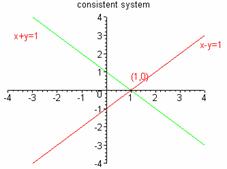
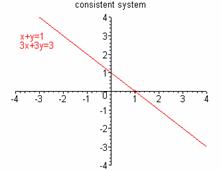
Independent System Dependent system
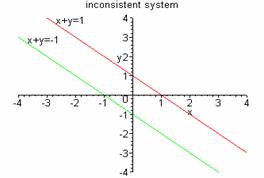
When it does not have a solution, it is called inconsistent. An inconsistent system does not have any point of intersection.
The graph of the two
equations shows that they are parallel and have no point of
intersection. An inconsistent system has no solution.
A solution to a system of linear equations can be found both graphically and algebraically.
You can plot the graph of a linear equation by means of a table of values, that is, by plotting the ordered pairs of numbers listed in the table. Find a small number of solutions of each equation, then plot these points, and finally join them using a smooth graph. Provided the lines are not parallel, the point of intersection would provide us with a set of coordinates that simultaneously satisfies both equations.
Solve using graphical
method ![]()
Solution:
For x + y
= 4 First: Determine the intercepts set x = 0, (0) + y = 4, y = 4. set y = 0, x + (0) = 4, x = 4. We have the points (0, 4) and (4, 0). Then: Plot the intercepts and finally,
graph a straight line through them.
For x - y
= 2 Determine the intercepts set x = 0, (0) - y = 2, y = -2. set y = 0, x - (0) = 2, x = 2. We have the points (0, -2) and (2, 0). Plot the intercepts and graph a straight line through
them.
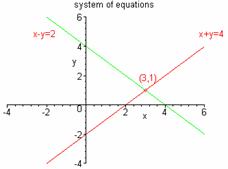
POINT OF INTERSECTION:
(3, 1)
a) Solve using graphical method ![]()
b)Solve using graphical
method ![]()
The graphical method is not the most efficient method for obtaining the solution since its accuracy depends upon the skills of the individual in constructing the two graphs and in estimating the coordinates of the point of intersection of the two equations. There are two algebraic methods that could help us determine the solution more easily and more accurately. These two methods are called elimination method (also called addition method) and the substitution method.
Step 1: Select one of the two variables that would be easier to eliminate. Select the variable whose coefficients have different signs or whose coefficients are equal in both equations.
Step 2: Find the least common multiple (LCD) of the coefficients of the selected variable and multiply the terms of each equation by the quotient of the LCD and the coefficient of the selected variable in that equation.
Step 3: Make sure that the signs of the selected variables are different (a plus and a minus sign) and the coefficients without the signs are equal.
Step 4: Add the two equations and solve for the remaining variable. Substitute the value of the solved variable in one of the given equation and solve for the other unknown.
Solve the system of
equations 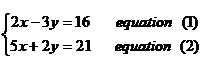
Solution: We select to eliminate the variable y since its coefficients have opposite signs. The LCD of y coefficients = 6.
Multiple first equation by 2 (we divided 6 by 3)
Multiple second equation by 3 ( we divided 6 by 2)
![]()
![]() =
= ![]()
![]() Add: 19x = 95
Add: 19x = 95 ![]() x = 5
x = 5
Since x = 5, 2(5) 3y = 16 ![]() 10 3y = 16
10 3y = 16 ![]() -3y = 16 10
-3y = 16 10 ![]() -3y = 6y = -2
-3y = 6y = -2
Solution (5, -2).
a) Solve the system of equations ![]()
b) Solve the system of equations ![]()
Solve the system of
equations ![]()
Solution: we can rewrite the two equations in the form ![]()
![]()
That is ![]() =
= ![]()
Since both variables have coefficients which are equal in both equations, we can choose any one of the variables. Lets choose x. The LCM = 1. Therefore we have
![]()
![]() =
= ![]()
Add:0 + 0 = -8 ![]() this is a false statement.
this is a false statement.
The system has no solution.
a) Solve the system of equations ![]()
b) Solve the system of equations ![]()
Example 5
Solve the system of
equations ![]()
Solution: we can rewrite the two equations in the form ![]()
![]()
![]() =
= ![]()
![]()
Lets eliminate the variable x. The LCM = 3. Therefore we have,
![]()
![]() =
= ![]()
Add: 0 +
0 = 0 ![]() this is a true statement.
this is a true statement.
There are infinitely many solutions (all real numbers).
a)Solve the system of
equations ![]()
b)Solve the system of
equations ![]()
Step 1: Choose one of the equations and solve for one of the variables in terms of the other. It is easier to choose the equation with variables that have a numerical coefficient of 1 or -1.
For example given the
system of equations ![]()
Since x in equation (1) has a coefficient of 1, we will solve x in terms of y for equation (1). Therefore, we will write x = 4 3y.
Step 2: Substitute the solved equation, x = 4 3y, in the other equation, (2x 5y = 12), to obtain one equation in one variable. Using our example above to illustrate this step, we have:
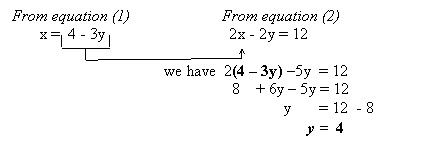
![]()
Step 3: Substitute the value of the variable obtained in any of the equations. Calculate the value of the remaining variable. Again, using our example to illustrate this step, we have:
From equation (1)x = 4 3y since y = 4 we have x = 4 3(4) = 4 12 = -8,x = -8.
The solution is x = -8, y = 4 or (-8, 4).
Example 6
Solve the system of equations using substitution. ![]()
![]()
Solution: ![]() =
= ![]()
From equation (1)
From
equation (2) x = 5 - y x + 2y = 8 (5 y) + 2y = 8 5 y + 2y = 8 y = 8 - 5 y = 3 x = 5 3
= 2 . Therefore we have x = 2, y =
3 or (2, 3)
a) Solve the system of equations using the
substitution method. ![]()
b) Solve the system of equations using the
substitution method. ![]()
Example 7
Solve the system of
equations using the substitution method. ![]()
Solution: ![]() =
= ![]() =
= 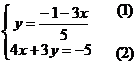
From equation (1)
From
equation (2) y = 4x + 3 20x + 3(-1 3x) = -25 20x 3 9x = - 25 11x = -25 + 3 11x = - 22 x = -2 y = Therefore
we have x = -2, y = 1 or (-2, 1)
![]() 4x + 3y = -5
4x + 3y = -5![]() = -5 LCD = 5
= -5 LCD = 5![]()
Check: ![]() =
= ![]()
a) Solve the system of equations using the
substitution method. ![]()
b) Solve the system of equations using the
substitution method. ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 530
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved